Cicloide

ImprimirCitar

Curva trazada por un punto en un círculo rodante

Un cicloide generado por un círculo rodante

En geometría, una cicloide es la curva trazada por un punto en un círculo mientras rueda a lo largo de una línea recta sin deslizarse. Una cicloide es una forma específica de trocoide y es un ejemplo de una ruleta, una curva generada por una curva rodando sobre otra curva.

La cicloide, con las cúspides apuntando hacia arriba, es la curva de descenso más rápido bajo gravedad uniforme (la curva braquistócrona). También es la forma de una curva para la cual el período de un objeto en movimiento armónico simple (subiendo y bajando repetidamente) a lo largo de la curva no depende de la posición inicial del objeto (la curva tautocrona).

Historia

Fue en el punto de prueba de mano izquierda del Pequod, con la piedra de jabón que me rodeaba diligentemente, que fui golpeado indirectamente por el hecho notable, que en la geometría todos los cuerpos deslizando a lo largo del cicloide, mi piedra de jabón, por ejemplo, descenderán de cualquier punto en precisamente el mismo tiempo.

Moby Dick por Herman Melville, 1851

La cicloide ha sido llamada "La Helena de los geómetras" ya que provocó frecuentes disputas entre los matemáticos del siglo XVII.

Los historiadores de las matemáticas han propuesto varios candidatos para el descubridor de la cicloide. El historiador matemático Paul Tannery citó un trabajo similar del filósofo sirio Jámblico como evidencia de que la curva se conocía en la antigüedad. El matemático inglés John Wallis, que escribió en 1679, atribuyó el descubrimiento a Nicolás de Cusa, pero los estudios posteriores indican que Wallis estaba equivocado o que la evidencia que usó ahora se ha perdido. El nombre de Galileo Galilei se propuso a fines del siglo XIX y al menos un autor informa que se le dio crédito a Marin Mersenne. Comenzando con el trabajo de Moritz Cantor y Siegmund Günther, los académicos ahora asignan prioridad al matemático francés Charles de Bovelles basándose en su descripción de la cicloide en su Introductio in geometriam, publicada en 1503. En este trabajo, Bovelles confunde el arco trazado por una rueda rodante como parte de un círculo más grande con un radio 120% más grande que la rueda más pequeña.

Galileo originó el término cicloide y fue el primero en hacer un estudio serio de la curva. Según su alumno Evangelista Torricelli, en 1599 Galileo intentó la cuadratura de la cicloide (determinando el área debajo de la cicloide) con un enfoque inusualmente empírico que implicó trazar tanto el círculo generador como la cicloide resultante en láminas de metal, cortarlas y pesarlas.. Descubrió que la proporción era aproximadamente 3:1, que es el valor real, pero concluyó incorrectamente que la proporción era una fracción irracional, lo que habría hecho imposible la cuadratura. Alrededor de 1628, Gilles Persone de Roberval probablemente se enteró del problema de la cuadratura de Père Marin Mersenne y efectuó la cuadratura en 1634 utilizando el Teorema de Cavalieri. Sin embargo, esta obra no se publicó hasta 1693 (en su Traité des Indivisibles).

La construcción de la tangente de la cicloide data de agosto de 1638 cuando Mersenne recibió métodos únicos de Roberval, Pierre de Fermat y René Descartes. Mersenne pasó estos resultados a Galileo, quien se los dio a sus alumnos Torricelli y Viviana, quienes pudieron producir una cuadratura. Este resultado y otros fueron publicados por Torricelli en 1644, que es también el primer trabajo impreso sobre la cicloide. Esto llevó a Roberval a acusar a Torricelli de plagio, con la controversia interrumpida por la temprana muerte de Torricelli en 1647.

En 1658, Blaise Pascal había dejado las matemáticas por la teología pero, mientras sufría de dolor de muelas, comenzó a considerar varios problemas relacionados con la cicloide. Su dolor de muelas desapareció, y lo tomó como una señal celestial para continuar con su investigación. Ocho días después había terminado su ensayo y, para dar a conocer los resultados, propuso un concurso. Pascal proponía tres preguntas relativas al centro de gravedad, el área y el volumen de la cicloide, recibiendo el ganador o ganadores premios de 20 y 40 doblones españoles. Pascal, Roberval y el senador Carcavy fueron los jueces, y ninguna de las dos presentaciones (de John Wallis y Antoine de Lalouvère) se consideró adecuada. Mientras el concurso estaba en curso, Christopher Wren envió a Pascal una propuesta para una prueba de la rectificación de la cicloide; Roberval afirmó rápidamente que conocía la prueba desde hacía años. Wallis publicó la prueba de Wren (acreditando a Wren) en Tractus Duo de Wallis, dando prioridad a Wren para la primera prueba publicada.

Quince años después, Christiaan Huygens utilizó el péndulo cicloidal para mejorar los cronómetros y descubrió que una partícula atravesaría un segmento de un arco cicloidal invertido en la misma cantidad de tiempo, independientemente de su punto de partida. En 1686, Gottfried Wilhelm Leibniz usó geometría analítica para describir la curva con una sola ecuación. En 1696, Johann Bernoulli planteó el problema de la braquistocrona, cuya solución es una cicloide.

Ecuaciones

La cicloide a través del origen, generada por un círculo de radio $r$ rodando sobre el $x$ -eje en el lado positivo ( $y \geq 0$ ), consta de los puntos $(x, y)$ , con

{displaystyle {begin{aligned}x&=r(t-sin t)\y&=r(1-cos t),end{aligned}}}

t

t

() x, Sí.) = rt, r)

La ecuación cartesiana se obtiene resolviendo la ecuación $y$ para $t$ y sustituyendo en $x$ -ecuación:

{displaystyle x=rcos ^{-1}left(1-{frac {y}{r}}right)-{sqrt {y(2r-y)}},}

${displaystyle rcos !left({frac {x+{sqrt {y(2r-y)}}}{r}}right)+y=r.}$

Cuando $Sí.$ se considera una función de $x$ , el cicloides es diferente en todas partes excepto en los cusps en el $x$ -eje, con el derivado que tiende hacia $infty$ o $-infty$ cerca de un cusp. El mapa desde $t$ a $() x, Sí.)$ es diferente, de hecho de clase $C$ ^JUEGO, con derivación 0 en los cusps.

La pendiente del tangente al cicloides en el punto $(x,y)$ es dado por ${textstyle {frac {dy}{dx}}=cot({frac {t}{2}})}$ .

Un segmento cicloides de un cusp a otro se llama arco del cicloides, por ejemplo los puntos con ${displaystyle 0leq tleq 2pi }$ y ${displaystyle 0leq xleq 2pi }$ .

Considerando el cicloides como el gráfico de una función $y=f(x)$ , satisface la ecuación diferencial:

left({frac {dy}{dx}}right)^{2}={frac {2r}{y}}-1.

Involuta

Generación de la involuta de la cicloides desenrollando un alambre tenso colocado en medio arco cicloides (rojo marcado)

La involuta de la cicloide tiene exactamente la misma forma que la cicloide de la que se origina. Esto se puede visualizar como el camino trazado por la punta de un cable que inicialmente se encuentra en un medio arco de la cicloide: a medida que se desenrolla mientras permanece tangente a la cicloide original, describe una nueva cicloide (ver también péndulo cicloidal y longitud de arco).

Demostración

Demostración de las propiedades de la involuta de un cicloide

Esta demostración utiliza la definición de rueda rodante de cicloides, así como el vector de velocidad instantánea de un punto en movimiento, tangente a su trayectoria. En la imagen adyacente, $P_{1}$ y $P_{2}$ son dos puntos pertenecientes a dos círculos rodantes, con la base del primero justo encima de la parte superior del segundo. Inicialmente, $P_{1}$ y $P_{2}$ coinciden en el punto de intersección de los dos círculos. Cuando los círculos ruedan horizontalmente con la misma velocidad, $P_{1}$ y $P_{2}$ atravesar dos curvas cicloides. Considerando la línea roja que conecta $P_{1}$ y $P_{2}$ en un momento dado, uno prueba la línea es siempre tangente al arco inferior $P_{2}$ ortogonal al arco superior $P_{1}$ . Vamos $Q$ ser el punto en común entre los círculos superiores e inferiores en el momento dado. Entonces:

${displaystyle P_{1},Q,P_{2}}$ are colinear: indeed the equal rolling speed gives equal angles ${displaystyle {widehat {P_{1}O_{1}Q}}={widehat {P_{2}O_{2}Q}}}$ , and thus ${displaystyle {widehat {O_{1}QP_{1}}}={widehat {O_{2}QP_{2}}}}$ . The point $Q$ lies on the line ${displaystyle O_{1}O_{2}}$ therefore ${displaystyle {widehat {P_{1}QO_{1}}}+{widehat {P_{1}QO_{2}}}=pi }$ and analogously ${displaystyle {widehat {P_{2}QO_{2}}}+{widehat {P_{2}QO_{1}}}=pi }$ . From the equality of ${displaystyle {widehat {O_{1}QP_{1}}}}$ and ${displaystyle {widehat {O_{2}QP_{2}}}}$ one has that also ${displaystyle {widehat {P_{1}QO_{2}}}={widehat {P_{2}QO_{1}}}}$ . It follows ${displaystyle {widehat {P_{1}QO_{1}}}+{widehat {P_{2}QO_{1}}}=pi }$ .
If $A$ is the meeting point between the perpendicular from $P_{1}$ to the line segment ${displaystyle O_{1}O_{2}}$ and the tangent to the circle at $P_{2}$ then the triangle ${displaystyle P_{1}AP_{2}}$ is isosceles, as is easily seen from the construction: ${displaystyle {widehat {QP_{2}A}}={tfrac {1}{2}}{widehat {P_{2}O_{2}Q}}}$ and ${displaystyle {widehat {QP_{1}A}}={tfrac {1}{2}}{widehat {QO_{1}R}}=}$ ${displaystyle {tfrac {1}{2}}{widehat {QO_{1}P_{1}}}}$ . For the previous noted equality between ${displaystyle {widehat {P_{1}O_{1}Q}}}$ and ${displaystyle {widehat {QO_{2}P_{2}}}}$ then ${displaystyle {widehat {QP_{1}A}}={widehat {QP_{2}A}}}$ and ${displaystyle P_{1}AP_{2}}$ is isosceles.
Drawing from $P_{2}$ the orthogonal segment to ${displaystyle O_{1}O_{2}}$ , from $P_{1}$ the straight line tangent to the upper circle, and calling $B$ the meeting point, one sees that ${displaystyle P_{1}AP_{2}B}$ is a rhombus using the theorems on angles between parallel lines
Now consider the velocity $V_{2}$ of $P_{2}$ . It can be seen as the sum of two components, the rolling velocity $V_{a}$ and the drifting velocity $V_{d}$ , which are equal in modulus because the circles roll without skidding. $V_{d}$ is parallel to ${displaystyle P_{1}A}$ , while $V_{a}$ is tangent to the lower circle at $P_{2}$ and therefore is parallel to ${displaystyle P_{2}A}$ . The rhombus constituted from the components $V_{d}$ and $V_{a}$ is therefore similar (same angles) to the rhombus ${displaystyle BP_{1}AP_{2}}$ because they have parallel sides. Then $V_{2}$ , the total velocity of $P_{2}$ , is parallel to ${displaystyle P_{2}P_{1}}$ because both are diagonals of two rhombuses with parallel sides and has in common with ${displaystyle P_{1}P_{2}}$ the contact point $P_{2}$ . Thus the velocity vector $V_{2}$ lies on the prolongation of ${displaystyle P_{1}P_{2}}$ . Because $V_{2}$ is tangent to the cycloid at $P_{2}$ , it follows that also ${displaystyle P_{1}P_{2}}$ coincides with the tangent to the lower cycloid at $P_{2}$ .
Analogously, it can be easily demonstrated that ${displaystyle P_{1}P_{2}}$ is orthogonal to $V_{1}$ (the other diagonal of the rhombus).
This proves that the tip of a wire initially stretched on a half arch of the lower cycloid and fixed to the upper circle at $P_{1}$ will follow the point along its path without changing its length because the speed of the tip is at each moment orthogonal to the wire (no stretching or compression). The wire will be at the same time tangent at $P_{2}$ to the lower arc because of the tension and the facts demonstrated above. (If it were not tangent there would be a discontinuity at $P_{2}$ and consequently unbalanced tension forces.)

Área

Utilizando la parametrización anterior ${textstyle x=r(t-sin t), y=r(1-cos t)}$ , el área bajo un arco, ${displaystyle 0leq tleq 2pi}$ es dado por:

{displaystyle A=int _{x=0}^{2pi r}y,dx=int _{t=0}^{2pi }r^{2}(1-cos t)^{2}dt=3pi r^{2}.}

Esto es tres veces el área del círculo rodante. Este y otros resultados similares se pueden obtener geométricamente sin cálculo mediante el cálculo visual de Mamikon.

Longitud de arco

La longitud de la cicloides como consecuencia de la propiedad de su involuta

La longitud del arco $S$ de un arco viene dada por

{displaystyle {begin{aligned}S&=int _{0}^{2pi }{sqrt {left({frac {dx}{dt}}right)^{2}+left({frac {dy}{dt}}right)^{2}}}dt\&=int _{0}^{2pi }r{sqrt {2-2cos t}},dt\&=2rint _{0}^{2pi }sin {frac {t}{2}},dt\&=8r.end{aligned}}}

Otra forma geométrica de calcular la longitud de la cicloide es notar que cuando un alambre que describe una evoluta se ha desenrollado completamente de medio arco, se extiende a lo largo de dos diámetros, una longitud de $4 r$ . Esto es así igual a la mitad de la longitud del arco, y la de un arco completo es $8 r$ .

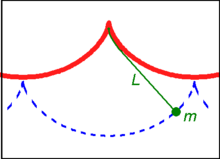
Péndulo cicloidal

Esquema de un péndulo cicloides.

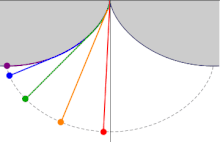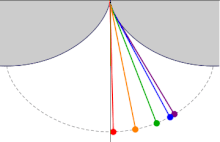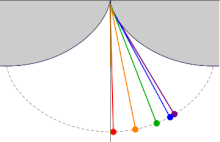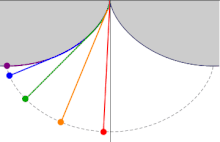
Si un péndulo simple está suspendido de la cúspide de una cicloide invertida, tal que la cuerda está restringida a ser tangente a uno de sus arcos, y la longitud del péndulo L es igual a la de la mitad de la longitud del arco de la cicloide (es decir, el doble del diámetro del círculo generador, L = 4r), la lenteja del péndulo también traza una trayectoria cicloide. Tal péndulo es isócrono, con oscilaciones de tiempo igual independientemente de la amplitud. Introduciendo un sistema de coordenadas centrado en la posición de la cúspide, la ecuación de movimiento viene dada por:

{displaystyle {begin{aligned}x&=r[2theta (t)+sin 2theta (t)]\y&=r[-3-cos 2theta (t)],end{aligned}}}

theta

{displaystyle sin theta (t)=Acos(omega t),qquad omega ^{2}={frac {g}{L}}={frac {g}{4r}},}

A 1

omega

Cinco pendula cicloidal isocrona con diferentes amplitudes.

El matemático holandés del siglo XVII Christiaan Huygens descubrió y probó estas propiedades de la cicloide mientras buscaba diseños de relojes de péndulo más precisos para usar en la navegación.

Curvas relacionadas

Varias curvas están relacionadas con la cicloide.

Trochoide: generalización de un cicloides en el que el punto de rastreo de la curva puede estar dentro del círculo de rodamiento (curtate) o exterior (prolate).
Hypocycloid: variante de un cicloides en el que un círculo rueda en el interior de otro círculo en lugar de una línea.
Epicicloide: variante de un cicloide en el que un círculo rueda en el exterior de otro círculo en lugar de una línea.
Hipotrocoide: generalización de una hipocicloide donde el punto de generación puede no estar en el borde del círculo de rodamiento.
Epitrocoide: generalización de un epicicloide donde el punto de generación puede no estar en el borde del círculo de rodamiento.

Todas estas curvas son ruletas con un círculo rodado a lo largo de otra curva de curvatura uniforme. Las cicloides, epicicloides e hipocicloides tienen la propiedad de que cada una es similar a su evoluta. Si q es el producto de esa curvatura con el radio del círculo, con signo positivo para epi- y negativo para hipo-, entonces la razón de similitud de la curva a la evoluta es 1 + 2 q.

El clásico juguete Spirograph traza las curvas hipotrocoide y epitrocoide.

Otros usos

Arcos Cycloidales en el Museo de Arte Kimbell

El arco cicloidal fue utilizado por el arquitecto Louis Kahn en su diseño para el Museo de Arte Kimbell en Fort Worth, Texas. También fue utilizado por Wallace K. Harrison en el diseño del Centro Hopkins en Dartmouth College en Hanover, New Hampshire.

Las primeras investigaciones indicaron que algunas curvas arqueadas transversales de las placas de los violines de la edad de oro están estrechamente modeladas por curvas cicloides cortadas. Trabajos posteriores indican que las cicloides curvadas no sirven como modelos generales para estas curvas, que varían considerablemente.

Contenido relacionado

Más resultados...