Ciclo oto

ImprimirCitar

Ciclo termodinámico para motores de encendido de chispa

Presión oto ciclo – diagrama de volumen

Diagrama de temperatura-entropía
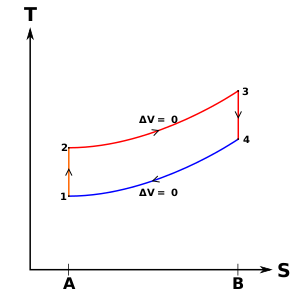
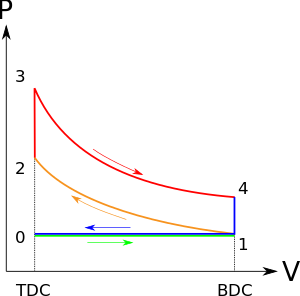
Los diagramas idealizados de un ciclo de cuatro tiempos Otto Ambos diagramas: la ingesta (A y color verde) trazo se realiza por una expansión isobarica, seguida de una compresión adiabática (B y color naranja) golpe. A través de la combustión de combustible, el calor se añade en un proceso constante de volumen (proceso isocópico), seguido de un proceso de expansión adiabática (materia) C y color rojo) golpe. El ciclo está cerrado por el escape (pertura) D y azul de color) trazo, caracterizado por el enfriamiento isocópico y los procesos de compresión isobarico.

Un ciclo de Otto es un ciclo termodinámico idealizado que describe el funcionamiento de un motor de pistón de encendido por chispa típico. Es el ciclo termodinámico que se encuentra más comúnmente en los motores de los automóviles.

El ciclo de Otto es una descripción de lo que le sucede a un gas cuando está sujeto a cambios de presión, temperatura, volumen, adición de calor y eliminación de calor. El gas que está sujeto a esos cambios se llama sistema. El sistema, en este caso, se define como el fluido (gas) dentro del cilindro. Al describir los cambios que ocurren dentro del sistema, también describirá a la inversa, el efecto del sistema sobre el medio ambiente. En el caso del ciclo Otto, el efecto será producir suficiente trabajo neto del sistema para impulsar un automóvil y sus ocupantes en el medio ambiente.

El ciclo de Otto se construye a partir de:

Parte superior e inferior del bucle: un par de procesos cuasi-paralelos e isentropicos (sin fricción, reversible adiabático).

Lados izquierdo y derecho del lazo: un par de procesos isocópicos paralelos (volumen constante).

El proceso isoentrópico de compresión o expansión implica que no habrá ineficiencia (pérdida de energía mecánica), y no habrá transferencia de calor dentro o fuera del sistema durante ese proceso. Se supone que el cilindro y el pistón son impermeables al calor durante ese tiempo. Se realiza trabajo sobre el sistema durante el proceso de compresión isoentrópica inferior. El calor fluye hacia el ciclo Otto a través del proceso de presurización de la izquierda y parte de él regresa a través del proceso de despresurización de la derecha. La suma del trabajo agregado al sistema más el calor agregado menos el calor eliminado da como resultado el trabajo mecánico neto generado por el sistema.

Procesos

Los procesos son descritos por:

Proceso 0-1 una masa de aire se dibuja en disposición de pistón / cilindro a presión constante.
Proceso 1–2 es una compresión adiabática (isentropic) de la carga mientras el pistón se mueve desde el centro de la muerte inferior (BDCarriba centro muertoTDC).
El proceso 2–3 es una transferencia de calor de volumen constante al gas de trabajo de una fuente externa, mientras que el pistón está en el centro superior muerto. Este proceso tiene por objeto representar el encendido de la mezcla de combustible-aire y la consiguiente quema rápida.
El proceso 3-4 es una expansión adiabática (isentropica) (pozo de poder).
Proceso 4–1 completa el ciclo por un proceso de volumen constante en el que el calor es rechazado desde el aire mientras que el pistón está en el centro inferior muerto.
Proceso 1–0 la masa de aire se libera a la atmósfera en un proceso de presión constante.

El ciclo de Otto consta de compresión isentrópica, adición de calor a volumen constante, expansión isentrópica y rechazo de calor a volumen constante. En el caso de un ciclo Otto de cuatro tiempos, técnicamente hay dos procesos adicionales: uno para el escape de calor residual y productos de combustión a presión constante (isobárico), y otro para la entrada de aire rico en oxígeno frío también a presión constante; sin embargo, estos a menudo se omiten en un análisis simplificado. Aunque esos dos procesos son críticos para el funcionamiento de un motor real, donde los detalles de la transferencia de calor y la química de la combustión son relevantes, para el análisis simplificado del ciclo termodinámico, es más conveniente suponer que todo el calor residual es eliminado durante un solo cambio de volumen.

Historia

Alphonse Beau de Rochas patentó por primera vez el motor de cuatro tiempos en 1861. Antes, entre 1854 y 1857, dos italianos (Eugenio Barsanti y Felice Matteucci) inventaron un motor que se rumoreaba que era muy similar, pero la patente se perdió.

La primera persona en construir un motor de cuatro tiempos en funcionamiento, un motor estacionario que utiliza una mezcla de aire y gas de carbón como combustible (un motor de gas), fue el ingeniero alemán Nicolaus Otto. Esta es la razón por la cual el principio de cuatro tiempos hoy en día se conoce comúnmente como el ciclo Otto y los motores de cuatro tiempos que usan bujías a menudo se denominan motores Otto.

Procesos

El sistema se define como la masa de aire que se extrae de la atmósfera hacia el cilindro, se comprime con el pistón, se calienta con la ignición por chispa del combustible agregado y se le permite expandirse a medida que empuja el pistón., y finalmente agotado de nuevo en la atmósfera. Se sigue la masa de aire a medida que cambia su volumen, presión y temperatura durante los diversos pasos termodinámicos. Como el pistón es capaz de moverse a lo largo del cilindro, el volumen del aire cambia con su posición en el cilindro. Los procesos de compresión y expansión inducidos en el gas por el movimiento del pistón se idealizan como reversibles, es decir, no se pierde trabajo útil por turbulencia o fricción y no se transfiere calor hacia o desde el gas durante esos dos procesos. La energía se agrega al aire por la combustión del combustible. El trabajo útil se extrae por la expansión del gas en el cilindro. Una vez completada la expansión en el cilindro, se extrae el calor restante y, finalmente, el gas se expulsa al medio ambiente. Durante el proceso de expansión se produce un trabajo mecánico útil y parte del mismo se usa para comprimir la masa de aire del siguiente ciclo. El trabajo mecánico útil producido menos el utilizado para el proceso de compresión es el trabajo neto ganado y que puede utilizarse para la propulsión o para impulsar otras máquinas. Alternativamente, el trabajo útil ganado es la diferencia entre el calor agregado y el calor eliminado.

Proceso 0–1 carrera de admisión (sombra azul)

Una masa de aire (fluido de trabajo) ingresa al cilindro, de 0 a 1, a presión atmosférica (presión constante) a través de la válvula de admisión abierta, mientras que la válvula de escape está cerrada durante este proceso. La válvula de admisión se cierra en el punto 1.

Proceso 1–2 carrera de compresión (B en los diagramas)

El pistón se mueve desde el extremo del cigüeñal (BDC, punto muerto inferior y volumen máximo) hasta el extremo de la culata (TDC, punto muerto superior y volumen mínimo) a medida que el gas de trabajo con el estado inicial 1 se comprime isentrópicamente al punto 2, mediante la relación de compresión $(V 1 / V 2)$ . Mecánicamente, esta es la compresión isoentrópica de la mezcla de aire y combustible en el cilindro, también conocida como carrera de compresión. Este proceso isoentrópico asume que no se pierde energía mecánica debido a la fricción y que no se transfiere calor hacia o desde el gas, por lo que el proceso es reversible. El proceso de compresión requiere que se agregue trabajo mecánico al gas de trabajo. Generalmente, la relación de compresión es de alrededor de 9–10:1 $(V 1 : V 2)$ para un motor típico.

Fase de encendido del proceso 2–3 (C en los diagramas)

El pistón descansa momentáneamente en TDC. Durante este instante, que se conoce como fase de encendido, la mezcla de aire/combustible permanece en un pequeño volumen en la parte superior del trazo de compresión. El calor se añade al fluido de trabajo por la combustión del combustible inyectado, con el volumen esencialmente mantenido constante. La presión aumenta y la relación $(P_{3}/P_{2})$ se llama "la relación de expansión".

Proceso 3–4 carrera de expansión (D en los diagramas)

El aumento de la presión alta ejerce una fuerza sobre el pistón y lo empuja hacia el BDC. La expansión del fluido de trabajo tiene lugar isótropicamente y el trabajo es realizado por el sistema en el pistón. La relación de volumen $V_{4}/V_{3}$ se llama la " ratio de expansión histrópica". (Para el ciclo Otto es el mismo que la relación de compresión $V_{1}/V_{2}$ ). Mecánicamente esta es la expansión de la mezcla gaseosa caliente en el cilindro conocido como expansión (potencia).

Proceso 4–1 rechazo de calor idealizado (A en los diagramas)

El pistón está momentáneamente en reposo en BDC. La presión del gas de trabajo cae instantáneamente del punto 4 al punto 1 durante un proceso de volumen constante a medida que el calor se elimina a un sumidero externo idealizado que se pone en contacto con la culata. En los motores de combustión interna modernos, el disipador de calor puede ser el aire circundante (para motores de baja potencia) o un fluido en circulación, como el refrigerante. El gas ha vuelto al estado 1.

Proceso 1–0 carrera de escape

La válvula de escape se abre en el punto 1. A medida que el pistón se mueve de "BDC" (punto 1) a "TDC" (punto 0) con la válvula de escape abierta, la mezcla gaseosa se ventila a la atmósfera y el proceso comienza de nuevo.

Análisis de ciclos

En los procesos 1 y 2, el pistón realiza trabajo sobre el gas y en los procesos 3 y 4, el gas realiza trabajo sobre el pistón durante los procesos de compresión y expansión isoentrópica, respectivamente. Los procesos 2–3 y 4–1 son procesos isocóricos; el calor se transfiere al sistema desde 2-3 y sale del sistema desde 4-1, pero no se realiza trabajo en el sistema ni se extrae del sistema durante esos procesos. No se realiza trabajo durante un proceso isocórico (volumen constante) porque la adición o eliminación de trabajo de un sistema requiere el movimiento de los límites del sistema; por lo tanto, como el volumen del cilindro no cambia, no se agrega ni elimina trabajo del eje del sistema.

Se utilizan cuatro ecuaciones diferentes para describir esos cuatro procesos. Se hace una simplificación al suponer que los cambios de energía cinética y potencial que tienen lugar en el sistema (masa de gas) pueden despreciarse y luego aplicar la primera ley de la termodinámica (conservación de energía) a la masa de gas a medida que cambia de estado como se caracteriza por la temperatura, presión y volumen del gas.

Durante un ciclo completo, el gas vuelve a su estado original de temperatura, presión y volumen, por lo que el cambio de energía interna neta del sistema (gas) es cero. Como resultado, la energía (calor o trabajo) añadida al sistema debe compensarse con la energía (calor o trabajo) que sale del sistema. En el análisis de sistemas termodinámicos, la convención es contabilizar la energía que ingresa al sistema como positiva y la energía que sale del sistema como negativa.

Ecuación 1a.

Durante un ciclo completo, el cambio neto de energía del sistema es cero:

{displaystyle Delta E=E_{text{in}}-E_{text{out}}=0}

Lo anterior establece que el sistema (la masa de gas) vuelve al estado termodinámico original en el que se encontraba al comienzo del ciclo.

Donde $E_{text{in}}$ es la energía agregada al sistema de 1–2–3 y $E_{text{out}}$ se elimina energía del sistema de 3-4-1. En términos de trabajo y calor añadido al sistema

Ecuación 1b:

W_{1-2}+Q_{2-3}+W_{3-4}+Q_{4-1}=0

Cada término de la ecuación se puede expresar en términos de la energía interna del gas en cada punto del proceso:

{displaystyle W_{1-2}=U_{2}-U_{1}}

{displaystyle Q_{2-3}=U_{3}-U_{2}}

{displaystyle W_{3-4}=U_{4}-U_{3}}

{displaystyle Q_{4-1}=U_{1}-U_{4}}

La Ecuación 1b del balance de energía se convierte en

{displaystyle W_{1-2}+Q_{2-3}+W_{3-4}+Q_{4-1}=left(U_{2}-U_{1}right)+left(U_{3}-U_{2}right)+left(U_{4}-U_{3}right)+left(U_{1}-U_{4}right)=0}

Para ilustrar el ejemplo, elegimos algunos valores para los puntos de la ilustración:

{displaystyle U_{1}=1}

{displaystyle U_{2}=5}

{displaystyle U_{3}=9}

{displaystyle U_{4}=4}

Estos valores se seleccionan de forma arbitraria pero racional. Entonces se pueden calcular los términos de trabajo y calor.

La energía añadida al sistema como trabajo durante la compresión de 1 a 2 es

{displaystyle left(U_{2}-U_{1}right)=left(5-1right)=4}

La energía añadida al sistema como calor desde el punto 2 al 3 es

{displaystyle left({U_{3}-U_{2}}right)=left(9-5right)=4}

La energía extraída del sistema como trabajo durante la expansión de 3 a 4 es

{displaystyle left(U_{4}-U_{3}right)=left(4-9right)=-5}

La energía extraída del sistema como calor del punto 4 al 1 es

{displaystyle left(U_{1}-U_{4}right)=left(1-4right)=-3}

El balance de energía es

{displaystyle Delta E=+4+4-5-3=0}

Tenga en cuenta que la energía añadida al sistema se cuenta como positiva y la energía que sale del sistema se cuenta como negativa y la suma es cero como se esperaba para un ciclo completo que devuelve el sistema a su estado original.

Desde el balance de energía, el trabajo del sistema es:

{displaystyle sum {text{Work}}=W_{1-2}+W_{3-4}=left(U_{2}-U_{1}right)+left(U_{4}-U_{3}right)=4-5=-1}

La energía neta que sale del sistema como trabajo es -1, lo que significa que el sistema ha producido una unidad neta de energía que sale del sistema en forma de trabajo.

El calor neto que sale del sistema es:

{displaystyle sum {text{Heat}}=Q_{2-3}+Q_{4-1}=left(U_{3}-U_{2}right)+left(U_{1}-U_{4}right)=4-3=1}

Como energía añadida al sistema en forma de calor es positivo. De lo anterior parece como si el sistema ganara una unidad de calor. Esto coincide con la energía producida por el sistema como trabajo fuera del sistema.

La eficiencia térmica es el cociente entre el trabajo neto del sistema y el calor agregado al sistema. Ecuación 2:

{displaystyle eta ={frac {W_{1-2}+W_{3-4}}{Q_{2-3}}}={frac {left(U_{2}-U_{1}right)+left(U_{4}-U_{3}right)}{left(U_{3}-U_{2}right)}}}

{displaystyle eta =1+{frac {U_{1}-U_{4}}{left(U_{3}-U_{2}right)}}=1+{frac {(1-4)}{(9-5)}}=0.25}

Alternativamente, la eficiencia térmica puede derivarse estrictamente del calor agregado y el calor rechazado.

{displaystyle eta ={frac {Q_{2-3}+Q_{4-1}}{Q_{2-3}}}=1+{frac {left(U_{1}-U_{4}right)}{left(U_{3}-U_{2}right)}}}

Suministro de valores ficticios

${displaystyle eta =1+{frac {1-4}{9-5}}=1+{frac {-3}{4}}=0.25}$

En el ciclo de Otto, no hay transferencia de calor durante los procesos 1–2 y 3–4, ya que son procesos isoentrópicos. El calor se suministra solo durante los procesos de volumen constante 2–3 y el calor se rechaza solo durante los procesos de volumen constante 4–1.

Los valores anteriores son valores absolutos que pueden, por ejemplo, tener unidades de joules (suponiendo que se utilice el sistema de unidades MKS) y serían útiles para un motor particular con dimensiones particulares. En el estudio de los sistemas termodinámicos, las cantidades extensivas como la energía, el volumen o la entropía (frente a las cantidades intensivas de temperatura y presión) se colocan sobre la base de la unidad de masa, al igual que los cálculos, haciéndolos más generales y, por lo tanto, más generales. usar. Por lo tanto, cada término que implica una cantidad extensiva podría dividirse por la masa, dando los términos unidades de julios/kg (energía específica), metros³/kg (volumen específico) o julios/(kelvin· kg) (entropía específica, capacidad calorífica), etc. y se representaría con letras minúsculas, u, v, s, etc.

La ecuación 1 ahora se puede relacionar con la ecuación de calor específico para volumen constante. Los calores específicos son particularmente útiles para los cálculos termodinámicos que involucran el modelo de gas ideal.

C_{text{v}}=left({frac {delta u}{delta T}}right)_{text{v}}

Reorganización de los rendimientos:

delta u=(C_{text{v}})(delta T)

Insertar la ecuación de calor específico en la ecuación de eficiencia térmica (Ecuación 2) produce.

eta =1-left({frac {C_{text{v}}(T_{4}-T_{1})}{C_{text{v}}(T_{3}-T_{2})}}right)

Al reorganizar:

eta =1-left({frac {T_{1}}{T_{2}}}right)left({frac {T_{4}/T_{1}-1}{T_{3}/T_{2}-1}}right)

Siguiente, notando de los diagramas $T_{4}/T_{1}=T_{3}/T_{2}$ (ver relaciones isentrópicas para un gas ideal), por lo tanto ambos pueden omitirse. La ecuación entonces reduce a:

Ecuación 2:

eta =1-left({frac {T_{1}}{T_{2}}}right)

& 4.

Ecuación 3:

left({frac {T_{2}}{T_{1}}}right)=left({frac {p_{2}}{p_{1}}}right)^{(gamma -1)/{gamma }}

Ecuación 4:

left({frac {T_{2}}{T_{1}}}right)=left({frac {V_{1}}{V_{2}}}right)^{(gamma -1)}

Donde

{gamma }=left({frac {C_{text{p}}}{C_{text{v}}}}right)

{gamma }

es la relación de calor específica

La derivación de las ecuaciones anteriores se encuentran resolviendo estas cuatro ecuaciones respectivamente (donde

R

es la constante de gas específica:

C_{text{p}}ln left({frac {V_{1}}{V_{2}}}right)-Rln left({frac {p_{2}}{p_{1}}}right)=0

C_{text{v}}ln left({frac {T_{2}}{T_{1}}}right)-Rln left({frac {V_{2}}{V_{1}}}right)=0

C_{text{p}}=left({frac {gamma R}{gamma -1}}right)

C_{text{v}}=left({frac {R}{gamma -1}}right)

Mayor simplificación de la Ecuación 4, donde $r$ es la relación de compresión $(V_{1}/V_{2})$ :

Ecuación 5:

left({frac {T_{2}}{T_{1}}}right)=left({frac {V_{1}}{V_{2}}}right)^{(gamma -1)}=r^{(gamma -1)}

Al invertir la Ecuación 4 e insertarla en la Ecuación 2, la eficiencia térmica final se puede expresar como:

Ecuación 6:

eta =1-left({frac {1}{r^{(gamma -1)}}}right)

De analizar la ecuación 6 es evidente que la eficiencia del ciclo Otto depende directamente de la relación de compresión $r$ . Desde $gamma$ para el aire es 1.4, un aumento en $r$ producirá un aumento en $eta$ . Sin embargo, el $gamma$ para productos de combustión de la mezcla de combustible/aire se toma a menudo aproximadamente 1.3. El debate anterior implica que es más eficiente tener una alta relación de compresión. La relación estándar es de aproximadamente 10:1 para automóviles típicos. Generalmente esto no aumenta mucho debido a la posibilidad de autoignición, o "knock", que coloca un límite superior en la relación de compresión. Durante el proceso de compresión 1–2 la temperatura aumenta, por lo que un aumento en la relación de compresión provoca un aumento de la temperatura. La autoignición ocurre cuando la temperatura de la mezcla de combustible/aire se vuelve demasiado alta antes de que se encienda por el frente de la llama. El trazo de compresión está destinado a comprimir los productos antes de que la llama encienda la mezcla. Si aumenta la relación de compresión, la mezcla puede encenderse automáticamente antes de que el trazo de compresión esté completo, lo que conduce a "toque de motor". Esto puede dañar los componentes del motor y disminuir la potencia de freno del motor.

Poder

La energía producida por el ciclo de Otto es una energía desarrollada por unidad de tiempo. Los motores Otto se denominan motores de cuatro tiempos. La carrera de admisión y la carrera de compresión requieren una rotación del cigüeñal del motor. La carrera de potencia y la carrera de escape requieren otra rotación. Para dos rotaciones hay un golpe generador de trabajo.

Del análisis del ciclo anterior, el trabajo neto producido por el sistema:

{displaystyle sum {text{ Work}}=W_{1-2}+W_{3-4}=left(U_{2}-U_{1}right)+left(U_{4}-U_{3}right)=+4-5=-1}

(nuevamente, usando la convención de signos, el signo menos implica que la energía sale del sistema como trabajo)

Si las unidades utilizadas fueran MKS, el ciclo habría producido un julio de energía en forma de trabajo. Para un motor de una cilindrada particular, como un litro, la masa de gas del sistema se puede calcular asumiendo que el motor está funcionando a temperatura estándar (20 °C) y presión (1 atm). Usando la Ley Universal de los Gases, la masa de un litro de gas está a temperatura ambiente y presión a nivel del mar:

M={frac {PV}{RT}}

V=0,001 m³, R=0,286 kJ/(kg·K), T=293 K, P=101,3 kN/m²

M=0,00121 kg

A una velocidad del motor de 3000 RPM hay 1500 golpes de trabajo/minuto o 25 golpes de trabajo/segundo.

{displaystyle sum {text{ Work}}=1,{text{J}}/({text{kg}}cdot {text{stroke}})times 0.00121,{text{kg}}=0.00121,{text{J}}/{text{stroke}}}

La potencia es 25 veces mayor ya que hay 25 golpes de trabajo/segundo

{displaystyle P=25times 0.00121=0.0303,{text{J}}/{text{s}};{text{or}};{text{W}}}

Si el motor utiliza varios cilindros con la misma cilindrada, el resultado se multiplicaría por el número de cilindros. Estos resultados son el producto de los valores de la energía interna que se supusieron para los cuatro estados del sistema al final de cada uno de los cuatro golpes (dos rotaciones). Fueron seleccionados solo con fines ilustrativos y obviamente son de poco valor. La sustitución de los valores reales de un motor real produciría resultados más cercanos a los del motor. Cuyos resultados serían más altos que el motor real ya que hay muchas suposiciones simplificadoras hechas en el análisis que pasan por alto las ineficiencias. Tales resultados sobrestimarían la potencia de salida.

Aumento de la potencia y la eficiencia

La diferencia entre las presiones y temperaturas de admisión y escape significa que se puede obtener un aumento en la eficiencia mediante el uso de un turbocompresor, eliminando del flujo de escape parte de la energía restante y transfiriéndola al flujo de admisión para aumentar la admisión. presión. Una turbina de gas puede extraer energía de trabajo útil de la corriente de escape y luego se puede usar para presurizar el aire de admisión. La presión y la temperatura de los gases de escape se reducirían a medida que se expanden a través de la turbina de gas y ese trabajo se aplica luego a la corriente de gas de admisión, aumentando su presión y temperatura. La transferencia de energía equivale a una mejora de la eficiencia y también se mejora la densidad de potencia resultante del motor. El aire de admisión generalmente se enfría para reducir su volumen, ya que el trabajo producido por carrera es una función directa de la cantidad de masa que ingresa al cilindro; el aire más denso producirá más trabajo por ciclo. Hablando en términos prácticos, la temperatura de la masa de aire de admisión también debe reducirse para evitar la ignición prematura en un motor de gasolina; por lo tanto, se utiliza un intercooler para extraer algo de energía en forma de calor y así reducir la temperatura de admisión. Tal esquema aumenta tanto la eficiencia como la potencia del motor.

La aplicación de un sobrealimentador accionado por el cigüeñal aumenta la potencia de salida (densidad de potencia), pero no aumenta la eficiencia, ya que utiliza parte del trabajo neto producido por el motor para presurizar el aire de admisión y no extrae la energía desperdiciada. asociado con el flujo de escape a alta temperatura y una presión al ambiente.

Contenido relacionado

Más resultados...

Ciclo oto

Procesos

Historia

Procesos

Proceso 0–1 carrera de admisión (sombra azul)

Proceso 1–2 carrera de compresión (B en los diagramas)

Fase de encendido del proceso 2–3 (C en los diagramas)

Proceso 3–4 carrera de expansión (D en los diagramas)

Proceso 4–1 rechazo de calor idealizado (A en los diagramas)

Proceso 1–0 carrera de escape

Análisis de ciclos

Poder

Aumento de la potencia y la eficiencia

Contenido relacionado

Eje

Laboratorio de tierra

TAT-10