Centroide

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Significa ("promedio") posición de todos los puntos en forma

Centroide de un triángulo

En matemáticas y física, el centroide, también conocido como centro geométrico o centro de figura, de una figura plana o figura sólida es la posición media aritmética de todos los puntos en la superficie de la figura. La misma definición se extiende a cualquier objeto en el espacio euclidiano n-dimensional.

En geometría, a menudo se asume una densidad de masa uniforme, en cuyo caso el baricentro o centro de masa coincide con el centroide. Informalmente, puede entenderse como el punto en el que un recorte de la forma (con una masa uniformemente distribuida) podría equilibrarse perfectamente en la punta de un alfiler.

En física, si se consideran las variaciones en la gravedad, un centro de gravedad se puede definir como la media ponderada de todos los puntos ponderados por su peso específico.

En geografía, el centroide de una proyección radial de una región de la superficie de la Tierra al nivel del mar es el centro geográfico de la región.

Historia

El término "centroide" es de acuñación reciente (1814). Se utiliza como sustituto de los términos más antiguos "centro de gravedad" y "centro de masa" cuando se deben enfatizar los aspectos puramente geométricos de ese punto. El término es peculiar del idioma inglés; los franceses, por ejemplo, usan "centre de gravité" en la mayoría de las ocasiones, y en otras se emplean términos de similar significado.

El centro de gravedad, como su nombre lo indica, es una noción que surgió en la mecánica, muy probablemente en relación con las actividades de construcción. No está claro cuándo apareció la idea por primera vez, ya que el concepto probablemente se le ocurrió a muchas personas individualmente con diferencias menores. No obstante, el centro de gravedad de las figuras fue ampliamente estudiado en la Antigüedad; Bossut le da crédito a Arquímedes (287-212 a. C.) por ser el primero en encontrar el centroide de las figuras planas, aunque nunca lo define. Se ha perdido un tratamiento de los centroides de los sólidos por parte de Arquímedes.

Es poco probable que Arquímedes aprendiera el teorema de que las medianas de un triángulo se encuentran en un punto, el centro de gravedad del triángulo, directamente de Euclides, ya que esta proposición no se encuentra en los Elementos. La primera afirmación explícita de esta proposición se debe a Garza de Alejandría (quizás el siglo I d. C.) y se encuentra en su Mecánica. Puede agregarse, de paso, que la proposición no se volvió común en los libros de texto sobre geometría plana hasta el siglo XIX.

Propiedades

El centroide geométrico de un objeto convexo siempre se encuentra en el objeto. Un objeto no convexo podría tener un centroide fuera de la figura misma. El centroide de un anillo o un cuenco, por ejemplo, se encuentra en el vacío central del objeto.

Si se define el centroide, es un punto fijo de todas las isometrías en su grupo de simetría. En particular, el centroide geométrico de un objeto se encuentra en la intersección de todos sus hiperplanos de simetría. El centroide de muchas figuras (polígono regular, poliedro regular, cilindro, rectángulo, rombo, círculo, esfera, elipse, elipsoide, superelipse, superelipsoide, etc.) puede determinarse únicamente por este principio.

En particular, el centroide de un paralelogramo es el punto de encuentro de sus dos diagonales. Esto no es cierto para otros cuadriláteros.

Por la misma razón, el centroide de un objeto con simetría de traslación no está definido (o se encuentra fuera del espacio que lo encierra), porque una traslación no tiene un punto fijo.

Ejemplos

El baricentro de un triángulo es la intersección de las tres medianas del triángulo (cada mediana conecta un vértice con el punto medio del lado opuesto).

Para conocer otras propiedades del centroide de un triángulo, consulte a continuación.

Ubicar

Método de la plomada

El centroide de una lámina plana uniformemente densa, como en la figura (a) a continuación, se puede determinar experimentalmente usando una plomada y un alfiler para encontrar el centro de masa coubicado de un cuerpo delgado de densidad uniforme que tiene la misma forma. El cuerpo está sostenido por el alfiler, insertado en un punto, fuera del presunto centroide de tal manera que puede girar libremente alrededor del alfiler; luego se deja caer la plomada del pasador (figura b). La posición de la plomada se traza en la superficie y el procedimiento se repite con el alfiler insertado en cualquier punto diferente (o varios puntos) fuera del centroide del objeto. El único punto de intersección de estas líneas será el baricentro (figura c). Siempre que el cuerpo tenga una densidad uniforme, todas las líneas hechas de esta manera incluirán el centroide y todas las líneas se cruzarán exactamente en el mismo lugar.


a)	b)	c)

Este método se puede extender (en teoría) a formas cóncavas donde el centroide puede estar fuera de la forma y virtualmente a sólidos (nuevamente, de densidad uniforme), donde el centroide puede estar dentro del cuerpo. Las posiciones (virtuales) de las plomadas deben registrarse por otros medios que no sean dibujándolas a lo largo de la forma.

Método de equilibrio

Para formas bidimensionales convexas, el centroide se puede encontrar equilibrando la forma con una forma más pequeña, como la parte superior de un cilindro angosto. El centroide se encuentra en algún lugar dentro del rango de contacto entre las dos formas (y exactamente en el punto donde la forma se equilibraría en un alfiler). En principio, se pueden usar cilindros progresivamente más estrechos para encontrar el centroide con precisión arbitraria. En la práctica, las corrientes de aire hacen que esto no sea factible. Sin embargo, al marcar el rango de superposición de múltiples balances, se puede lograr un nivel considerable de precisión.

De un conjunto finito de puntos

El centroide de un conjunto finito de $k$ puntos $mathbf {x} _{1},mathbf {x} _{2},ldotsmathbf {x} _{k}$ dentro $mathbb {R} ^{n}$ es

{displaystyle mathbf {C} ={frac {mathbf {x} _{1}+mathbf {x} _{2}+cdots +mathbf {x} _{k}}{k}}.}

Por descomposición geométrica

El centroide de una figura de avión $X$ se puede calcular dividiéndolo en un número finito de figuras más simples $X_{1},X_{2},dotsX_{n}$ , computando el centroide $C_{i}$ y zona $A_{i}$ de cada parte, y luego computar

{displaystyle C_{x}={frac {sum _{i}{C_{i}}_{x}A_{i}}{sum _{i}A_{i}}},C_{y}={frac {sum _{i}{C_{i}}_{y}A_{i}}{sum _{i}A_{i}}}}

Agujeros en la figura $X$ , superposiciones entre las partes, o partes que se extienden fuera de la figura se pueden manejar todos utilizando áreas negativas $A_{i}$ . Es decir, las medidas $A_{i}$ debe tomarse con signos positivos y negativos de tal manera que la suma de los signos $A_{i}$ para todas las partes que encierran un punto dado $p$ 1 si $p$ pertenece $X$ , y 0 de lo contrario.

Por ejemplo, la siguiente figura (a) se divide fácilmente en un cuadrado y un triángulo, ambos con área positiva; y un agujero circular, con área negativa (b).

a) Objeto 2D

b) Objeto descrito usando elementos más simples

c) Centros de elementos del objeto

El centroide de cada parte se puede encontrar en cualquier lista de centroides de formas simples (c). Entonces el centroide de la figura es el promedio ponderado de los tres puntos. La posición horizontal del centroide, desde el borde izquierdo de la figura es

{displaystyle x={frac {5times 10^{2}+13.33times {frac {1}{2}}10^{2}-3times pi 2.5^{2}}{10^{2}+{frac {1}{2}}10^{2}-pi 2.5^{2}}}approx 8.5{text{ units}}.}

La misma fórmula sostiene para cualquier objeto tridimensional, excepto que cada uno $A_{i}$ debe ser el volumen de $X_{i}$ en lugar de su área. También tiene para cualquier subconjunto de $mathbb {R} ^{d}$ , para cualquier dimensión $d$ , con las áreas sustituidas por $d$ - medidas dimensionales de las partes.

Por fórmula integral

El centroide de un subconjunto X de $mathbb {R} ^{n}$ también puede ser calculado por la integral

{displaystyle C={frac {int xg(x);dx}{int g(x);dx}}}

mathbb {R} ^{n}

gXXX

Otra fórmula para el centroide es

{displaystyle C_{k}={frac {int zS_{k}(z);dz}{int g(x);dx}}}

C_kkCS_kzXx_kzX

Para una figura plana, en particular, las coordenadas del baricentro son

{displaystyle C_{mathrm {x} }={frac {int xS_{mathrm {y} }(x);dx}{A}}}

{displaystyle C_{mathrm {y} }={frac {int yS_{mathrm {x} }(y);dy}{A}}}

donde A es el área de la figura X; S_y(x) es la longitud de la intersección de X con la línea vertical en la abscisa x; y S_x(y) es la cantidad análoga para los ejes intercambiados.

De una región delimitada

El centroide $({bar {x}},;{bar {y}})$ de una región atada por los gráficos de las funciones continuas $f$ y $g$ tales que $f(x)geq g(x)$ en el intervalo $[a,b]$ , $aleq xleq b$ , se da por

{displaystyle {bar {x}}={frac {1}{A}}int _{a}^{b}x[f(x)-g(x)];dx}

{displaystyle {bar {y}}={frac {1}{A}}int _{a}^{b}left[{frac {f(x)+g(x)}{2}}right][f(x)-g(x)];dx,}

Donde $A$ es la zona de la región (por ${textstyle int _{a}^{b}left[f(x)-g(x)right]dx}$ ).

Con una integral

Se puede usar una integral (un pariente del planímetro) para encontrar el centroide de un objeto de forma irregular con un límite suave (o suave por partes). El principio matemático involucrado es un caso especial del teorema de Green.

De un objeto en forma de L

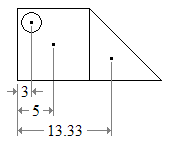
Este es un método para determinar el centroide de un objeto en forma de L.

Divide la forma en dos rectángulos, como se muestra en la figura 2. Encuentra los centroides de estos dos rectángulos dibujando las diagonales. Dibuja una línea que se une a los centroides. El centroide de la forma debe estar en esta línea AB.
Divide la forma en otros dos rectángulos, como se muestra en la higuera 3. Encuentra los centroides de estos dos rectángulos dibujando las diagonales. Dibuja una línea que se une a los centroides. El centroide de la forma L debe estar en esta línea CD.
Como el centroide de la forma debe estar a lo largo de AB y también a lo largo de CD, debe estar en la intersección de estas dos líneas, en O. El punto O podría estar dentro o fuera del objeto en forma de L.

De un triángulo

El centroide de un triángulo es el punto de intersección de sus medianas (las líneas que unen cada vértice con el punto medio del lado opuesto). El centroide divide cada una de las medianas en la relación 2:1, que es decir que se encuentra 1⁄3 de la distancia de cada lado al vértice opuesto (ver cifras a la derecha). Sus coordenadas cartesianas son los medios de las coordenadas de los tres vértices. Es decir, si los tres vértices son $L=(x_{L},y_{L}),$ $M=(x_{M},y_{M}),$ y $N=(x_{N},y_{N}),$ entonces el centroide (denotado C aquí pero más comúnmente denotado G en la geometría del triángulo)

{displaystyle C={frac {1}{3}}(L+M+N)=left({frac {1}{3}}(x_{L}+x_{M}+x_{N}),;;{frac {1}{3}}(y_{L}+y_{M}+y_{N})right).}

Por lo tanto, el centroide está en ${tfrac {1}{3}}:{tfrac {1}{3}}:{tfrac {1}{3}}$ en coordenadas baricéntricos.

En coordenadas trilineales, el centroide se puede expresar de cualquiera de estas formas equivalentes en términos de las longitudes de los lados a, b, c y los ángulos de los vértices L, M, N:

{displaystyle {begin{aligned}C&={frac {1}{a}}:{frac {1}{b}}:{frac {1}{c}}=bc:ca:ab=csc L:csc M:csc N\[6pt]&=cos L+cos Mcdot cos N:cos M+cos Ncdot cos L:cos N+cos Lcdot cos M\[6pt]&=sec L+sec Mcdot sec N:sec M+sec Ncdot sec L:sec N+sec Lcdot sec M.end{aligned}}}

El centroide también es el centro de masa físico si el triángulo está hecho de una hoja uniforme de material; o si toda la masa se concentra en los tres vértices y se reparte equitativamente entre ellos. Por otro lado, si la masa se distribuye a lo largo del perímetro del triángulo, con densidad lineal uniforme, entonces el centro de masa se encuentra en el centro de Spieker (el incentro del triángulo medial), lo que (en general) no coincidir con el centroide geométrico del triángulo completo.

El área del triángulo es 1,5 veces la longitud de cualquier lado multiplicada por la distancia perpendicular del lado al centroide.

El baricentro de un triángulo se encuentra en su línea de Euler entre su ortocentro H y su circuncentro O, exactamente dos veces más cerca de este último que del primero:

{displaystyle {overline {CH}}=2{overline {CO}}.}

Además, para el incentro I y el centro de nueve puntos N, tenemos

<math alttext="{displaystyle {begin{aligned}{overline {CH}}&=4{overline {CN}}\[5pt]{overline {CO}}&=2{overline {CN}}\[5pt]{overline {IC}}&<{overline {HC}}\[5pt]{overline {IH}}&<{overline {HC}}\[5pt]{overline {IC}}&CH̄ ̄ =4CN̄ ̄ CŌ ̄ =2CN̄ ̄ IC̄ ̄ .HC̄ ̄ IH̄ ̄ .HC̄ ̄ IC̄ ̄ .IŌ ̄ {fnK} {} {fn} {fn}} {}}} {fn} {fn} {}} {}} {fn}} {fn}} {fn}} {}} {fn}} {}} {}}} {}}} {}}}}} {}}}}} {}} {}}}}}}} {}}}}}}} {}}}}}}} {}}}}}}}}}} {}}}}}}}} {}}}}}}}} {}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}} {} {}}}}}}}}}}} {}}}}}}}}}}}}}}}} {}}}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}<img alt="{displaystyle {begin{aligned}{overline {CH}}&=4{overline {CN}}\[5pt]{overline {CO}}&=2{overline {CN}}\[5pt]{overline {IC}}&<{overline {HC}}\[5pt]{overline {IH}}&<{overline {HC}}\[5pt]{overline {IC}}&

Si G es el baricentro del triángulo ABC, entonces:

{displaystyle ({text{Area of }}triangle mathrm {ABG})=({text{Area of }}triangle mathrm {ACG})=({text{Area of }}triangle mathrm {BCG})={frac {1}{3}}({text{Area of }}triangle mathrm {ABC})}

Cualquiera de las tres medianas a través del centroide divide el área del triángulo por la mitad. Esto no es cierto para otras líneas a través del centroide; la desviación más grande de la división de áreas iguales ocurre cuando una línea a través del centroide es paralela a un lado del triángulo, creando un triángulo más pequeño y un trapezoide; en este caso el área del trapezoide es 5/9 del triángulo original.

Sea P cualquier punto en el plano de un triángulo con vértices A, B, y C y centroide G. Entonces la suma de las distancias al cuadrado de P desde los tres vértices excede la suma de las distancias al cuadrado del centroide G desde los vértices por tres veces la distancia al cuadrado entre P y G:

{displaystyle PA^{2}+PB^{2}+PC^{2}=GA^{2}+GB^{2}+GC^{2}+3PG^{2}.}

La suma de los cuadrados de los lados del triángulo es igual a tres veces la suma de las distancias al cuadrado del centroide desde los vértices:

{displaystyle AB^{2}+BC^{2}+CA^{2}=3(GA^{2}+GB^{2}+GC^{2}).}

El baricentro de un triángulo es el punto que maximiza el producto de las distancias dirigidas de un punto desde las líneas laterales del triángulo.

Sea ABC un triángulo, sea G su baricentro y sean D, E y F sean los puntos medios de BC, CA y AB, respectivamente. Para cualquier punto P en el plano de ABC entonces

{displaystyle PA+PB+PCleq 2(PD+PE+PF)+3PG.}

De un polígono

El centroide de un polígono cerrado que no se corta a sí mismo definido por n vértices (x₀,y₀), (x₁,y₁),..., (x_n−1,y_n−1) es el punto (C_x, C_y), donde

{displaystyle C_{mathrm {x} }={frac {1}{6A}}sum _{i=0}^{n-1}(x_{i}+x_{i+1})(x_{i} y_{i+1}-x_{i+1} y_{i}),}

{displaystyle C_{mathrm {y} }={frac {1}{6A}}sum _{i=0}^{n-1}(y_{i}+y_{i+1})(x_{i} y_{i+1}-x_{i+1} y_{i}),}

{displaystyle A={frac {1}{2}}sum _{i=0}^{n-1}(x_{i} y_{i+1}-x_{i+1} y_{i}).}

En estas fórmulas, se supone que los vértices se numeran en orden de su aparición a lo largo del perímetro del polígono; además, el vértice (x_n, Sí._n) se supone que es el mismo que (x₀, Sí.₀), que significa $i+1$ en el último caso debe bucle alrededor para $i = 0$ . (Si los puntos están numerados en el orden del reloj, el área A, computed as above, will be negative; however, the centroid coordinates will be correct even in this case.)

De un cono o pirámide

El centroide de un cono o pirámide se encuentra en el segmento de línea que conecta el vértice con el centroide de la base. Para un cono sólido o una pirámide, el centroide es 1/4 de la distancia desde la base hasta el vértice. Para un cono o pirámide que es solo una capa (hueco) sin base, el centroide es 1/3 de la distancia desde el plano base hasta el vértice.

De un tetraedro y símplex n-dimensional

Un tetraedro es un objeto en un espacio tridimensional que tiene cuatro triángulos como caras. Un segmento de recta que une un vértice de un tetraedro con el baricentro de la cara opuesta se llama mediana, y un segmento de recta que une los puntos medios de dos aristas opuestas se llama bimediana. Por lo tanto, hay cuatro medianas y tres bimedianas. Estos siete segmentos de línea se encuentran en el centroide del tetraedro. Las medianas se dividen por el baricentro en la razón 3:1. El baricentro de un tetraedro es el punto medio entre su punto Monge y el circuncentro (centro de la esfera circunscrita). Estos tres puntos definen la línea de Euler del tetraedro que es análoga a la línea de Euler de un triángulo.

Estos resultados se generalizan a cualquier n- simplex dimensional de la siguiente manera. Si el conjunto de vértices de un simplex es ${v_{0},ldotsv_{n}}$ , después considerando los vértices como vectores, el centroide es

{displaystyle C={frac {1}{n+1}}sum _{i=0}^{n}v_{i}.}

El centroide geométrico coincide con el centro de masa si la masa se distribuye uniformemente sobre todo el simplex, o se concentra en los vértices como n+1 masas iguales.

De un hemisferio

El centroide de un hemisferio sólido (es decir, la mitad de una bola sólida) divide el segmento de línea que conecta el centro de la esfera con el polo del hemisferio en una proporción de 3:5 (es decir, se encuentra a 3/8 del camino del centro al polo). El centroide de un hemisferio hueco (es decir, la mitad de una esfera hueca) divide por la mitad el segmento de línea que conecta el centro de la esfera con el polo del hemisferio.

Contenido relacionado

Más resultados...