Centralidad

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En teoría de grafos y análisis de redes, los indicadores de centralidad asignan números o clasificaciones a los nodos dentro de un gráfico correspondiente a su posición en la red. Las aplicaciones incluyen la identificación de la(s) persona(s) más influyente(s) en una red social, nodos de infraestructura clave en Internet o redes urbanas, súper propagadores de enfermedades y redes cerebrales. Los conceptos de centralidad se desarrollaron por primera vez en el análisis de redes sociales y muchos de los términos utilizados para medir la centralidad reflejan su origen sociológico.

Definición y caracterización de los índices de centralidad

Los índices de centralidad son respuestas a la pregunta "¿Qué caracteriza a un vértice importante?" La respuesta se da en términos de una función de valor real en los vértices de un gráfico, donde se espera que los valores producidos proporcionen una clasificación que identifique los nodos más importantes.

La palabra "importancia" tiene una gran cantidad de significados, lo que lleva a muchas definiciones diferentes de centralidad. Se han propuesto dos esquemas de categorización. La "importancia" puede concebirse en relación con un tipo de flujo o transferencia a través de la red. Esto permite clasificar las centralidades por el tipo de flujo que consideran importante. La "importancia" puede concebirse alternativamente como participación en la cohesión de la red. Esto permite clasificar las centralidades en función de cómo miden la cohesión. Ambos enfoques dividen las centralidades en distintas categorías. Otra conclusión es que una centralidad que es apropiada para una categoría a menudo "se equivocará" cuando se aplique a una categoría diferente.

Muchas medidas de centralidad, aunque no todas, cuentan efectivamente el número de caminos (también llamados paseos) de algún tipo que pasan por un vértice dado; las medidas difieren en cómo se definen y cuentan los paseos relevantes. Restringir la consideración a este grupo permite una taxonomía que coloca muchas centralidades en un espectro desde aquellas relacionadas con caminatas de longitud uno (centralidad de grado) hasta caminatas infinitas (centralidad de vector propio). Otras medidas de centralidad, como la centralidad de intermediación, se centran no solo en la conectividad general, sino también en ocupar posiciones que son fundamentales para la conectividad de la red.

Caracterización por flujos de red

Una red puede considerarse una descripción de los caminos a lo largo de los cuales fluye algo. Esto permite una caracterización basada en el tipo de flujo y el tipo de camino codificado por la centralidad. Un flujo puede basarse en transferencias, donde cada artículo indivisible va de un nodo a otro, como una entrega de paquetes que va del lugar de entrega a la casa del cliente. Un segundo caso es la duplicación en serie, en la que se replica un elemento para que tanto el origen como el destino lo tengan. Un ejemplo es la propagación de información a través de chismes, con la información siendo propagada de manera privada y con los nodos de origen y de destino siendo informados al final del proceso. El último caso es la duplicación paralela, con el elemento duplicado en varios enlaces al mismo tiempo,

Del mismo modo, el tipo de camino puede estar restringido a geodésicas (caminos más cortos), caminos (ningún vértice se visita más de una vez), senderos (los vértices se pueden visitar varias veces, ningún borde se recorre más de una vez) o paseos (vértices y los bordes se pueden visitar/atravesar varias veces).

Caracterización por estructura de paseo

Una clasificación alternativa puede derivarse de cómo se construye la centralidad. Esto nuevamente se divide en dos clases. Las centralidades son radiales o mediales. Las centralidades radiales cuentan los paseos que empiezan/terminan desde el vértice dado. Las centralidades de grado y valor propio son ejemplos de centralidades radiales, contando el número de caminatas de longitud uno o infinita. Las centralidades mediales cuentan los paseos que pasan por el vértice dado. El ejemplo canónico es la centralidad de intermediación de Freeman, el número de caminos más cortos que pasan por el vértice dado.

Asimismo, el conteo puede capturar el volumen o la duración de las caminatas. El volumen es el número total de caminatas del tipo dado. Los tres ejemplos del párrafo anterior entran en esta categoría. Longitud captura la distancia desde el vértice dado hasta los vértices restantes en el gráfico. La centralidad de cercanía, la distancia geodésica total desde un vértice dado a todos los demás vértices, es el ejemplo más conocido. Tenga en cuenta que esta clasificación es independiente del tipo de caminata contada (es decir, caminata, sendero, camino, geodésico).

Borgatti y Everett proponen que esta tipología proporciona información sobre la mejor manera de comparar las medidas de centralidad. Las centralidades colocadas en la misma casilla en esta clasificación 2×2 son lo suficientemente similares como para hacer alternativas plausibles; uno puede comparar razonablemente cuál es mejor para una aplicación dada. Las medidas de diferentes cajas, sin embargo, son categóricamente distintas. Cualquier evaluación de la aptitud relativa solo puede ocurrir dentro del contexto de predeterminar qué categoría es más aplicable, lo que hace que la comparación sea discutible.

Las centralidades de volumen radial existen en un espectro

La caracterización por estructura de paseo muestra que casi todas las centralidades de amplio uso son medidas de volumen radial. Estos codifican la creencia de que la centralidad de un vértice es una función de la centralidad de los vértices con los que está asociado. Las centralidades se distinguen en cómo se define la asociación.

Bonacich demostró que si la asociación se define en términos de caminatas, entonces se puede definir una familia de centralidades en función de la longitud de la caminata considerada. La centralidad de grado cuenta caminatas de longitud uno, mientras que la centralidad de valores propios cuenta caminatas de longitud infinita. Las definiciones alternativas de asociación también son razonables. La centralidad alfa permite que los vértices tengan una fuente de influencia externa. La centralidad del subgrafo de Estrada propone solo contar caminos cerrados (triángulos, cuadrados, etc.).

El corazón de tales medidas es la observación de que las potencias de la matriz de adyacencia del gráfico dan el número de caminatas de longitud dada por esa potencia. De manera similar, la matriz exponencial también está estrechamente relacionada con el número de caminatas de una longitud dada. Una transformación inicial de la matriz de adyacencia permite una definición diferente del tipo de caminata contada. Bajo cualquier enfoque, la centralidad de un vértice se puede expresar como una suma infinita, ya sea ${displaystyle sum_{k=0}^{infty}A_{R}^{k}beta^{k}}$

para potencias matriciales o ${displaystyle sum _{k=0}^{infty}{frac {(A_{R}beta)^{k}}{k!}}}$

para matrices exponenciales, donde

$k$ es la longitud de la caminata,
$ARKANSAS$ es la matriz de adyacencia transformada, y
$beta$ es un parámetro de descuento que asegura la convergencia de la suma.

La familia de medidas de Bonacich no transforma la matriz de adyacencia. La centralidad alfa reemplaza la matriz de adyacencia con su resolvente. La centralidad del subgrafo reemplaza la matriz de adyacencia con su rastro. Una conclusión sorprendente es que, independientemente de la transformación inicial de la matriz de adyacencia, todos estos enfoques tienen un comportamiento limitante común. A medida $beta$ que se acerca a cero, los índices convergen al grado de centralidad. A medida $beta$ que se acerca a su valor máximo, los índices convergen a la centralidad del valor propio.

Centralidad de la teoría de juegos

La característica común de la mayoría de las medidas estándar antes mencionadas es que evalúan la importancia de un nodo centrándose solo en el papel que desempeña un nodo por sí mismo. Sin embargo, en muchas aplicaciones tal enfoque es inadecuado debido a las sinergias que pueden ocurrir si el funcionamiento de los nodos se considera en grupos.

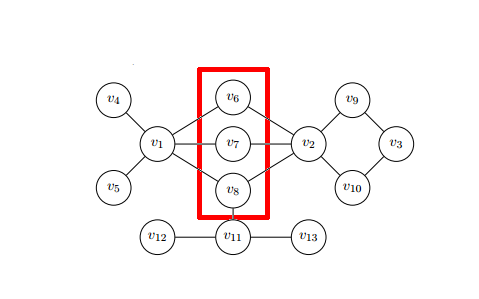
Ejemplo de centralidad de teoría de juegos

Por ejemplo, considere el problema de detener una epidemia. Mirando la imagen de arriba de la red, ¿qué nodos debemos vacunar? Según las medidas descritas anteriormente, queremos reconocer los ganglios que son los más importantes en la propagación de enfermedades. Los enfoques basados solo en centralidades, que se centran en las características individuales de los nodos, pueden no ser una buena idea. Los nodos en el cuadrado rojo, individualmente no pueden detener la propagación de la enfermedad, pero considerándolos como un grupo, vemos claramente que pueden detener la enfermedad si ha comenzado en los nodos $v_{1}$ , $v_4$ y $v_{5}$ . Las centralidades de la teoría de juegos intentan consultar los problemas y oportunidades descritos, utilizando herramientas de la teoría de juegos. El enfoque propuesto enutiliza el valor de Shapley. Debido a la dureza de la complejidad temporal del cálculo del valor de Shapley, la mayoría de los esfuerzos en este dominio se dirigen a implementar nuevos algoritmos y métodos que se basan en una topología peculiar de la red o un carácter especial del problema. Tal enfoque puede llevar a reducir la complejidad del tiempo de exponencial a polinomial.

De manera similar, la distribución de autoridad del concepto de solución () aplica el índice de poder de Shapley-Shubik, en lugar del valor de Shapley, para medir la influencia directa bilateral entre los jugadores. La distribución es de hecho un tipo de centralidad de vector propio. Se utiliza para clasificar objetos de big data en Hu (2020), como clasificar las universidades estadounidenses.

Limitaciones importantes

Los índices de centralidad tienen dos limitaciones importantes, una obvia y otra sutil. La limitación obvia es que una centralidad que es óptima para una aplicación a menudo es subóptima para una aplicación diferente. En efecto, si esto no fuera así, no necesitaríamos tantas centralidades diferentes. El gráfico de la cometa de Krackhardt proporciona una ilustración de este fenómeno, para el cual tres nociones diferentes de centralidad dan tres opciones diferentes del vértice más central.

La limitación más sutil es la falacia comúnmente sostenida de que la centralidad de los vértices indica la importancia relativa de los vértices. Los índices de centralidad están diseñados explícitamente para producir una clasificación que permita indicar los vértices más importantes. Esto lo hacen bien, bajo la limitación que acabamos de señalar. No están diseñados para medir la influencia de los nodos en general. Recientemente, los físicos de redes han comenzado a desarrollar métricas de influencia de nodos para abordar este problema.

El error es doble. En primer lugar, un ranking solo ordena los vértices por importancia, no cuantifica la diferencia de importancia entre los diferentes niveles del ranking. Esto puede mitigarse aplicando la centralización de Freeman a la medida de centralidad en cuestión, que proporciona una idea de la importancia de los nodos según las diferencias de sus puntajes de centralización. Además, la centralización de Freeman permite comparar varias redes comparando sus puntajes de centralización más altos. Este enfoque, sin embargo, rara vez se ve en la práctica.

En segundo lugar, las características que (correctamente) identifican los vértices más importantes en una red/aplicación dada no necesariamente se generalizan a los vértices restantes. Para la mayoría de los otros nodos de la red, las clasificaciones pueden no tener sentido. Esto explica por qué, por ejemplo, solo los primeros resultados de una búsqueda de imágenes de Google aparecen en un orden razonable. El pagerank es una medida muy inestable, que muestra reversiones de rango frecuentes después de pequeños ajustes del parámetro de salto.

Si bien el hecho de que los índices de centralidad no se generalicen al resto de la red puede parecer al principio contraintuitivo, se deriva directamente de las definiciones anteriores. Las redes complejas tienen una topología heterogénea. En la medida en que la medida óptima depende de la estructura de la red de los vértices más importantes, una medida óptima para tales vértices es subóptima para el resto de la red.

Grado de centralidad

Históricamente, el primero y conceptualmente más simple es el grado de centralidad, que se define como el número de enlaces que inciden en un nodo (es decir, el número de enlaces que tiene un nodo). El grado se puede interpretar en términos del riesgo inmediato de un nodo de atrapar cualquier cosa que fluya a través de la red (como un virus o alguna información). En el caso de una red dirigida (donde los lazos tienen dirección), generalmente definimos dos medidas separadas de centralidad de grado, a saber, grado de entrada y grado de salida. En consecuencia, el grado de entrada es un recuento del número de vínculos dirigidos al nodo y el grado de salida es el número de vínculos que el nodo dirige a otros. Cuando los lazos se asocian a algunos aspectos positivos como la amistad o la colaboración, el grado interior suele interpretarse como una forma de popularidad y el grado exterior como gregarismo.

El grado de centralidad de un vértice $v$ , para un grafo dado $G:=(V,E)$ con $|V|$ vértices y $|E|$ aristas, se define como $C_{D}(v)=grado(v)$

Calcular el grado de centralidad para todos los nodos en un gráfico toma $Theta(V^2)$ una representación de matriz de adyacencia densa del gráfico, y para los bordes toma $Theta(E)$ una representación de matriz dispersa.

La definición de centralidad a nivel de nodo se puede extender a todo el grafo, en cuyo caso estamos hablando de centralización de grafo. Sea $v*$ el nodo con mayor grado de centralidad en $GRAMO$ . Sea $X:=(Y,Z)$ el $|S|$ grafo conexo de nodos que maximiza la siguiente cantidad ( $y*$ siendo el nodo con mayor grado de centralidad en $X$ ): $H=sum_{{j=1}}^{{|Y|}}[C_{D}(y*)-C_{D}(y_{j})]$

En consecuencia, el grado de centralización del gráfico $GRAMO$ es el siguiente: ${displaystyle C_{D}(G)={frac {sum_i=1}^{|V|}[C_{D}(v*)-C_{D}(v_{i})] {H}}}$

El valor de $H$ se maximiza cuando el gráfico $X$ contiene un nodo central al que están conectados todos los demás nodos (un gráfico de estrella), y en este caso ${displaystyle H=(n-1)cdot ((n-1)-1)=n^{2}-3n+2.}$

Entonces, para cualquier gráfico ${ estilo de visualización G: = (V, E),}$ ${displaystyle C_{D}(G)={frac {sum_i=1}^{|V|}[C_{D}(v*)-C_{D}(v_{i})] }{|V|^{2}-3|V|+2}}}$

Además, una nueva medida global extensa para la centralidad del grado denominada Tendency to Make Hub (TMH) se define de la siguiente manera: ${displaystyle {text{TMH}}={frac {sum _{i=1}^{|V|}deg(v)^{2}}{sum _{i=1}^{ |V|}grado(v)}}}$

donde TMH aumenta por aparición de grado de centralidad en la red.

Cercanía centralidad

En un gráfico conectado, la centralidad de cercanía normalizada (o cercanía) de un nodo es la longitud promedio del camino más corto entre el nodo y todos los demás nodos en el gráfico. Por lo tanto, cuanto más central es un nodo, más cerca está de todos los demás nodos.

La cercanía fue definida por Alex Bavelas (1950) como el recíproco de la lejanía, es decir ${textstyle C_{B}(v)=(sum _{u}d(u,v))^{-1}}$ donde $d(u,v)$ está la distancia entre los vértices u y v. Sin embargo, cuando se habla de centralidad de cercanía, la gente suele referirse a su forma normalizada, dada por la fórmula anterior multiplicada por $N-1$ , donde $norte$ es el número de nodos en el gráfico ${displaystyle C(v)={frac {N-1}{sum _{u}d(u,v)}}.}$

Esta normalización permite comparaciones entre nodos de gráficos de diferentes tamaños. Para muchos gráficos, existe una fuerte correlación entre el inverso de la cercanía y el logaritmo de grado, donde es el grado del vértice v mientras que α y β son constantes para cada red. ${ estilo de visualización (C (v)) ^ {-1} aproximadamente - alfa ln (k_ {v}) + beta}$ ${displaystyle k_{v}}$

Tomar distancias desde o hacia todos los demás nodos es irrelevante en gráficos no dirigidos, mientras que puede producir resultados totalmente diferentes en gráficos dirigidos (por ejemplo, un sitio web puede tener una centralidad de cercanía alta del enlace saliente, pero una centralidad de cercanía baja de los enlaces entrantes).

Centralidad armónica

En un gráfico (no necesariamente conectado), la centralidad armónica invierte la suma y las operaciones recíprocas en la definición de centralidad de proximidad: ${displaystyle H(v)=sum_{u|uneq v}{frac {1}{d(u,v)}}}$

donde ${ estilo de visualización 1/d (u, v) = 0}$ si no hay camino de u a v. La centralidad armónica se puede normalizar dividiendo por $N-1$ , donde $norte$ es el número de nodos en el gráfico.

La centralidad armónica fue propuesta por Marchiori y Latora (2000) y luego de forma independiente por Dekker (2005), utilizando el nombre de "centralidad valorada", y por Rochat (2009).

Centralidad de intermediación

La intermediación es una medida de centralidad de un vértice dentro de un gráfico (también existe la intermediación de bordes, que no se analiza aquí). La centralidad de intermediación cuantifica el número de veces que un nodo actúa como puente a lo largo del camino más corto entre otros dos nodos. Linton Freeman lo introdujo como una medida para cuantificar el control de un humano sobre la comunicación entre otros humanos en una red social. En su concepción, los vértices que tienen una alta probabilidad de ocurrir en un camino más corto elegido al azar entre dos vértices elegidos al azar tienen una alta intermediación.

La intermediación de un vértice $v$ en un gráfico $G:=(V,E)$ con $V$ vértices se calcula de la siguiente manera:

Para cada par de vértices (s, t), calcule los caminos más cortos entre ellos.
Para cada par de vértices (s, t), determine la fracción de los caminos más cortos que pasan por el vértice en cuestión (aquí, el vértice v).
Sume esta fracción sobre todos los pares de vértices (s, t).

De manera más compacta, la intermediación se puede representar como: $C_B(v)= sum_{s neq v neq t in V}frac{sigma_{st}(v)}{sigma_{st}}$

donde $sigma_{st}$ es el número total de caminos más cortos de nodo $s$ a nodo $t$ y $sigma_{st}(v)$ es el número de esos caminos que pasan por $v$ . La intermediación se puede normalizar dividiendo el número de pares de vértices sin incluir v, que para gráficos dirigidos es $(n-1)(n-2)$ y para gráficos no dirigidos es $(n-1)(n-2)/2$ . Por ejemplo, en un gráfico estelar no dirigido, el vértice central (que está contenido en todos los caminos más cortos posibles) tendría una intermediación de $(n-1)(n-2)/2$ (1, si se normalizara) mientras que las hojas (que no están contenidas en caminos más cortos) tendrían una intermediación de 0.

Desde un aspecto de cálculo, las centralidades tanto de intermediación como de cercanía de todos los vértices en un gráfico implican calcular los caminos más cortos entre todos los pares de vértices en un gráfico, lo que requiere ${ estilo de visualización O (V ^ {3})}$ tiempo con el algoritmo de Floyd-Warshall. Sin embargo, en gráficos dispersos, el algoritmo de Johnson puede ser más eficiente y lleva $O(V^2 log V + VE)$ tiempo. En el caso de gráficos no ponderados, los cálculos se pueden realizar con el algoritmo de Brandes, que toma $O(VE)$ tiempo. Normalmente, estos algoritmos asumen que los gráficos no están dirigidos y están conectados con la posibilidad de bucles y múltiples aristas. Cuando se trata específicamente con gráficos de red, a menudo los gráficos no tienen bucles ni bordes múltiples para mantener relaciones simples (donde los bordes representan conexiones entre dos personas o vértices). En este caso, usar el algoritmo de Brandes dividirá las puntuaciones finales de centralidad por 2 para tener en cuenta que cada ruta más corta se cuenta dos veces.

Centralidad del vector propio

La centralidad del vector propio (también llamada centralidad propia) es una medida de la influencia de un nodo en una red. Asigna puntuaciones relativas a todos los nodos de la red basándose en el concepto de que las conexiones a los nodos con una puntuación alta contribuyen más a la puntuación del nodo en cuestión que las conexiones iguales a los nodos con una puntuación baja. El PageRank de Google y la centralidad de Katz son variantes de la centralidad del vector propio.

Uso de la matriz de adyacencia para encontrar la centralidad del vector propio

Para un grafo dado $G:=(V,E)$ con $|V|$ número de vértices, $A = (a_{v,t})$ sea la matriz de adyacencia, es decir, $a_{v,t} = 1$ si el vértice $v$ está vinculado al vértice $t$ , y en $a_{v,t} = 0$ caso contrario. La puntuación de centralidad relativa del vértice $v$ se puede definir como: $x_v = frac{1}{lambda} sum_{t in M(v)}x_t = frac{1}{lambda} sum_{t in G} a_{v,t}x_t$

donde $m(v)$ es un conjunto de vecinos de $v$ y $lambda$ es una constante. Con una pequeña reorganización, esto se puede reescribir en notación vectorial como la ecuación del vector propio $mathbf{Ax} = {lambda}mathbf{x}$

En general, habrá muchos valores propios diferentes $lambda$ para los que existe una solución de vector propio distinta de cero. Dado que las entradas en la matriz de adyacencia no son negativas, existe un único valor propio máximo, que es real y positivo, según el teorema de Perron-Frobenius. Este mayor valor propio da como resultado la medida de centralidad deseada. El $v^{th}$ componente del vector propio relacionado da la puntuación de centralidad relativa del vértice $v$ en la red. El vector propio solo se define hasta un factor común, por lo que solo las proporciones de las centralidades de los vértices están bien definidas. Para definir una puntuación absoluta, se debe normalizar el vector propio, por ejemplo, de modo que la suma de todos los vértices sea 1 o el número total de vértices n. La iteración de potencia es uno de los muchos algoritmos de valores propios que se pueden usar para encontrar este vector propio dominante. Además, esto se puede generalizar para que las entradas en A puedan ser números reales que representen las intensidades de conexión, como en una matriz estocástica.

Centralidad de Katz

La centralidad de Katz es una generalización de la centralidad de grado. La centralidad de grado mide el número de vecinos directos, y la centralidad de Katz mide el número de todos los nodos que se pueden conectar a través de un camino, mientras que las contribuciones de los nodos distantes se penalizan. Matemáticamente se define como $x_i = sum_{k=1}^{infin}sum_{j=1}^N alpha^k (A^k)_{ji}$

donde $alfa$ es un factor de atenuación en $(0,1)$ .

La centralidad de Katz puede verse como una variante de la centralidad del vector propio. Otra forma de centralidad de Katz es ${displaystyle x_{i}=alpha sum _{j=1}^{N}a_{ij}(x_{j}+1).}$

En comparación con la expresión de centralidad del vector propio, $x_{j}$ se reemplaza por ${ estilo de visualización x_ {j} + 1.}$

Se muestra que el vector propio principal (asociado con el valor propio más grande de $A$ , la matriz de adyacencia) es el límite de la centralidad de Katz cuando $alfa$ se aproxima ${ estilo de visualización { tfrac {1} { lambda}}}$ desde abajo.

Centralidad de PageRank

PageRank satisface la siguiente ecuación ${displaystyle x_{i}=alpha sum_{j}a_{ji}{frac {x_{j}}{L(j)}}+{frac {1-alpha }{N}},}$

dónde ${displaystyle L(j)=sum_{i}a_{ji}}$

es el número de vecinos del nodo $j$ (o el número de enlaces salientes en un gráfico dirigido). En comparación con la centralidad del vector propio y la centralidad de Katz, una diferencia importante es el factor de escala $L(j)$ . Otra diferencia entre PageRank y la centralidad del vector propio es que el vector PageRank es un vector propio de la izquierda (tenga en cuenta que el factor $a_{de}$ tiene los índices invertidos).

Centralidad de percolación

Existe una gran cantidad de medidas de centralidad para determinar la "importancia" de un solo nodo en una red compleja. Sin embargo, estas medidas cuantifican la importancia de un nodo en términos puramente topológicos, y el valor del nodo no depende de ningún modo del "estado" del nodo. Permanece constante independientemente de la dinámica de la red. Esto es cierto incluso para las medidas de intermediación ponderadas. Sin embargo, un nodo puede muy bien estar centralmente ubicado en términos de centralidad de intermediación u otra medida de centralidad, pero puede no estar 'centralmente' ubicado en el contexto de una red en la que hay filtración. La filtración de un 'contagio' ocurre en redes complejas en varios escenarios. Por ejemplo, la infección viral o bacteriana puede propagarse a través de las redes sociales de las personas, conocidas como redes de contacto. La propagación de enfermedades también se puede considerar en un nivel más alto de abstracción, contemplando una red de ciudades o centros de población conectados por carretera, ferrocarril o enlaces aéreos. Los virus informáticos pueden propagarse a través de las redes informáticas. Los rumores o noticias sobre ofertas y acuerdos comerciales también pueden difundirse a través de las redes sociales de las personas. En todos estos escenarios, un 'contagio' se propaga por los enlaces de una red compleja, alterando los 'estados' de los nodos a medida que se propaga, ya sea de manera recuperable o no. Por ejemplo, en un escenario epidemiológico, las personas pasan del estado 'susceptible' al estado 'infectado' a medida que se propaga la infección. Los estados que pueden tomar los nodos individuales en los ejemplos anteriores pueden ser binarios (como recibir/no recibir una noticia), discretos (susceptible/infectado/recuperado), o incluso continuo (como la proporción de personas infectadas en un pueblo), a medida que se propaga el contagio. La característica común en todos estos escenarios es que la propagación del contagio da como resultado el cambio de estado de los nodos en las redes. Con esto en mente, se propuso la centralidad de percolación (PC), que mide específicamente la importancia de los nodos en términos de ayudar a la percolación a través de la red. Esta medida fue propuesta por Piraveenan et al.

La centralidad de la filtración se define para un nodo dado, en un momento dado, como la proporción de 'caminos filtrados' que pasan por ese nodo. Una 'ruta filtrada' es la ruta más corta entre un par de nodos, donde el nodo de origen se filtra (p. ej., se infecta). El nodo de destino puede estar filtrado o no filtrado, o en un estado parcialmente filtrado. $PC^t(v)= frac{1}{N-2}sum_{s neq v neq r}frac{sigma_{sr}(v)}{sigma_{sr}}frac{ {x^t}_s}{{sum {[{x^t}_i}]}-{x^t}_v}$

donde $sigma_{sr}$ es el número total de caminos más cortos de nodo $s$ a nodo $r$ y $sigma_{sr}(v)$ es el número de esos caminos que pasan por $v$ . El estado de filtración del nodo $i$ en el momento $t$ se denota mediante ${x^t}_yo$ y dos casos especiales son cuando ${x^t}_i=0$ indica un estado sin filtración en el momento $t$ mientras ${x^t}_i=1$ que indica un estado totalmente filtrado en el momento $t$ . Los valores intermedios indican estados parcialmente filtrados (por ejemplo, en una red de municipios, este sería el porcentaje de personas infectadas en ese municipio).

Los pesos adjuntos a las rutas de percolación dependen de los niveles de percolación asignados a los nodos de origen, basados en la premisa de que cuanto más alto es el nivel de percolación de un nodo de origen, más importantes son las rutas que se originan en ese nodo. Los nodos que se encuentran en los caminos más cortos que se originan en nodos altamente filtrados son, por lo tanto, potencialmente más importantes para la filtración. La definición de PC también se puede ampliar para incluir también los pesos de los nodos de destino. Los cálculos de centralidad de percolación se ejecutan en el $EN M)$ tiempo con una implementación eficiente adoptada del algoritmo rápido de Brandes y si el cálculo debe tener en cuenta los pesos de los nodos objetivo, el tiempo en el peor de los casos es $O(N^{3})$ .

Centralidad entre camarillas

La centralidad entre camarillas de un solo nodo en un gráfico complejo determina la conectividad de un nodo con diferentes camarillas. Un nodo con alta conectividad cruzada facilita la propagación de información o enfermedad en un gráfico. Las camarillas son subgrafos en los que cada nodo está conectado a todos los demás nodos de la camarilla. La conectividad entre camarillas de un nodo $v$ para un grafo dado $G:=(V,E)$ con $|V|$ vértices y $|E|$ aristas, se define como $X(v)$ donde $X(v)$ es el número de camarillas a las que $v$ pertenece el vértice. Esta medida se utilizó en Everett y Borgatti, pero fue propuesta por primera vez en 1998, donde la llamaron centralidad de superposición de camarilla.

Centralización de hombre libre

La centralización de cualquier red es una medida de qué tan central es su nodo más central en relación con qué tan centrales son todos los demás nodos. Luego, las medidas de centralización (a) calculan la suma de las diferencias de centralidad entre el nodo más central de una red y todos los demás nodos; y (b) dividir esta cantidad por la suma de diferencias teóricamente mayor en cualquier red del mismo tamaño. Así, cada medida de centralidad puede tener su propia medida de centralización. Definido formalmente, si $C_x(p_i)$ es cualquier medida de centralidad del punto $i$ , si $C_x(p_*)$ es la mayor medida de este tipo en la red, y si: $max sum _{{i=1}}^{{N}}C_{x}(p_{*})-C_{x}(p_{i})$

es la mayor suma de diferencias en centralidad de puntos $C_{x}$ para cualquier gráfico con el mismo número de nodos, entonces la centralización de la red es: ${displaystyle C_{x}={frac {sum _{i=1}^{N}C_{x}(p_{*})-C_{x}(p_{i})}{max suma _{i=1}^{N}C_{x}(p_{*})-C_{x}(p_{i})}}.}$

El concepto se debe a Linton Freeman.

Medidas de centralidad basadas en la disimilitud

Para obtener mejores resultados en el ranking de los nodos de una red dada, se utilizan medidas de disimilitud (específicas de la teoría de clasificación y minería de datos) para enriquecer las medidas de centralidad en redes complejas. Esto se ilustra con la centralidad del vector propio, calculando la centralidad de cada nodo a través de la solución del problema del valor propio ${displaystyle Wmathbf {c} =lambda mathbf {c} }$

donde ${displaystyle W_{ij}=A_{ij}D_{ij}}$ (producto de coordenadas a coordenadas) y $D_{ij}$ es una matriz de disimilitud arbitraria, definida a través de una medida disimilitar, por ejemplo, disimilitud de Jaccard dada por ${displaystyle D_{ij}=1-{dfrac {|V^{+}(i)cap V^{+}(j)|}{|V^{+}(i)cup V^{ +}(j)|}}}$

Donde esta medida nos permite cuantificar la contribución topológica (por eso se llama centralidad de contribución) de cada nodo a la centralidad de un nodo dado, teniendo más peso/relevancia aquellos nodos con mayor disimilitud, ya que estos permiten al nodo dado acceso a nodos aquello a lo que ellos mismos no pueden acceder directamente.

Es de destacar que $W$ es no negativa porque $A$ y $D$ son matrices no negativas, por lo que podemos usar el teorema de Perron-Frobenius para asegurarnos de que el problema anterior tiene una solución única para λ = λ _max con c no negativa, lo que nos permite inferir la centralidad de cada nodo en la red. Por lo tanto, la centralidad del i-ésimo nodo es ${displaystyle c_{i}={dfrac {1}{n}}sum _{j=1}^{n}W_{ij}c_{j},,,,,,,i=1,cdots,n}$

donde $norte$ es el número de nodos en la red. Se probaron varias medidas de disimilitud y redes para obtener mejores resultados en los casos estudiados.

Contenido relacionado

Más resultados...