Célula Wigner-Seitz
El Celda Wigner-Seitz, nombrado por Eugene Wigner y Frederick Seitz, es una célula primitiva que se ha construido aplicando la descomposición de Voronoi a una celosía cristalina. Se utiliza en el estudio de materiales cristalinos en cristalografía.

La propiedad única de un cristal es que sus átomos están dispuestos en una matriz tridimensional regular llamada red. Todas las propiedades atribuidas a los materiales cristalinos provienen de esta estructura altamente ordenada. Tal estructura exhibe simetría traslacional discreta. Para modelar y estudiar un sistema periódico de este tipo, se necesita un "mango" describir la simetría y así sacar conclusiones sobre las propiedades materiales resultantes de esta simetría. La célula de Wigner-Seitz es un medio para lograrlo.
Una celda de Wigner-Seitz es un ejemplo de celda primitiva, que es una celda unitaria que contiene exactamente un punto de red. Para cualquier red dada, hay un número infinito de posibles celdas primitivas. Sin embargo, sólo hay una celda de Wigner-Seitz para cualquier red determinada. Es el lugar geométrico de los puntos en el espacio que están más cerca de ese punto de la red que de cualquiera de los otros puntos de la red.
Una celda de Wigner-Seitz, como cualquier celda primitiva, es un dominio fundamental para la simetría de traslación discreta de la red. La celda primitiva de la red recíproca en el espacio de momento se llama zona de Brillouin.
Descripción general
Fondo
El concepto de descomposición de Voronoi fue investigado por Peter Gustav Lejeune Dirichlet, lo que dio lugar al nombre dominio de Dirichlet. Se hicieron otras contribuciones de Evgraf Fedorov, (Paraleloedro de Fedorov), Georgy Voronoy (Poliedro de Voronoi) y Paul Niggli (Wirkungsbereich).
La aplicación para la física de materia condensada fue propuesta por primera vez por Eugene Wigner y Frederick Seitz en un papel de 1933, donde se utilizó para resolver la ecuación Schrödinger para electrones libres en sodio elemental. Se aproximaron a la forma de la célula Wigner-Seitz en sodio, que es un octaedro truncado, como esfera de igual volumen, y resolvieron la ecuación Schrödinger exactamente utilizando condiciones de límites periódicas, que requieren d↑ ↑ /dr=0{displaystyle dpsi /dr=0} en la superficie de la esfera. Un cálculo similar que también representaba la naturaleza no esférica de la célula Wigner-Seitz fue realizado más adelante por John C. Slater.
Solo hay cinco poliedros topológicamente distintos que mosaico el espacio tridimensional, ℝ3. Estos se conocen como paraleloedros. Son objeto de interés matemático, como en dimensiones superiores. Estos cinco paraleloedros se pueden utilizar para clasificar las redes tridimensionales utilizando el concepto de plano proyectivo, como lo sugieren John Horton Conway y Neil Sloane. Sin embargo, mientras que una clasificación topológica considera que cualquier transformación afín conduce a una clase idéntica, una clasificación más específica conduce a 24 clases distintas de poliedros voronoi con bordes paralelos que mosaico el espacio. Por ejemplo, el cuboide rectangular, el prisma cuadrado rectángulo y el cubo pertenecen a la misma clase topológica, pero se distinguen por diferentes proporciones de sus lados. Esta clasificación de los 24 tipos de poliedros voronoi para redes de Bravais fue establecida por primera vez por Boris Delaunay.
Definición
La celda de Wigner-Seitz alrededor de un punto de la red se define como el lugar geométrico de los puntos en el espacio que están más cerca de ese punto de la red que de cualquiera de los otros puntos de la red.
Se puede demostrar matemáticamente que una célula de Wigner-Seitz es una célula primitiva. Esto implica que la celda abarca todo el espacio directo sin dejar huecos ni agujeros, propiedad conocida como teselación.
Construyendo la celda
El concepto matemático general incorporado en una celda de Wigner-Seitz se llama más comúnmente celda de Voronoi, y la partición del plano en estas celdas para un conjunto dado de sitios puntuales se conoce como diagrama de Voronoi.

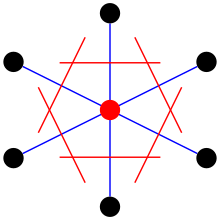
La célula puede ser elegida por primera vez eligiendo un punto de celo. Después de un punto es elegido, las líneas se dibujan a todos los puntos de celo cercanos. En el punto medio de cada línea, otra línea se dibuja normal a cada uno de los primeros conjuntos de líneas. El área más pequeña encerrada de esta manera se llama el Celda primitiva Wigner-Seitz.
Para una red tridimensional, los pasos son análogos, pero en el paso 2, en lugar de dibujar líneas perpendiculares, se dibujan planos perpendiculares en el punto medio de las líneas entre los puntos de la red.
Como en el caso de todas las celdas primitivas, toda el área o espacio dentro de la red puede ser llenado por celdas de Wigner-Seitz y no habrá espacios.
Los puntos de la red cercanos se examinan continuamente hasta que el área o volumen encerrado sea el área o volumen correcto para una celda primitiva. Alternativamente, si los vectores base de la red se reducen mediante reducción de red, solo es necesario utilizar un número determinado de puntos de red. En dos dimensiones, solo es necesario utilizar los puntos de la red que forman las 4 celdas unitarias que comparten un vértice con el origen. En tres dimensiones sólo es necesario utilizar los puntos de la red que forman las 8 celdas unitarias que comparten un vértice con el origen.
| Clase topológica (el afine equivalente paraleledro) | ||||||
|---|---|---|---|---|---|---|
| Truncado octaedro | Dodecaedro alargado | Rhombic dodecahedron | Prisma hexagonal | Cube | ||
| Bravais lattice | Primitivo cúbico | Cualquier | ||||
| Cobijo centrado en la cara | Cualquier | |||||
| Cobijo centrado en el cuerpo | Cualquier | |||||
| Hexagonal primitivo | Cualquier | |||||
| Primitive rhombohedral | 90^{circ }}" xmlns="http://www.w3.org/1998/Math/MathML">α α ■90∘ ∘ {displaystyle alpha >90^{circ } | <math alttext="{displaystyle alpha α α c)90∘ ∘ {displaystyle alpha<img alt="{displaystyle alpha | ||||
| Primitive tetragonal | Cualquier | |||||
| Tetragonal centrado en el cuerpo | <math alttext="{displaystyle c/ac/ac)2{displaystyle c/a meant{sqrt {2}}<img alt="{displaystyle c/a | {sqrt {2}}}" xmlns="http://www.w3.org/1998/Math/MathML">c/a■2{displaystyle c/a confidencial {2}} | ||||
| Orthorhombic primitivo | Cualquier | |||||
| Orthorhombic centrado en la base | Cualquier | |||||
| Ortomóbico centrado en la cara | Cualquier | |||||
| Orthorhombic centrado en el cuerpo | <math alttext="{displaystyle c^{2}c2c)a2+b2{displaystyle ¿Qué?<img alt="{displaystyle c^{2} | a^{2}+b^{2}}" xmlns="http://www.w3.org/1998/Math/MathML">c2■a2+b2{displaystyle c^{2} {2}+b^{2} | c2=a2+b2{displaystyle ¿Qué? | |||
| Primitivo monoclínico | Cualquier | |||||
| Monoclinico centrado en la base | <math alttext="{displaystyle aac)b{displaystyle a meantb}<img alt="{displaystyle a | b}" xmlns="http://www.w3.org/1998/Math/MathML">a■b{displaystyle a prendab} | b}" xmlns="http://www.w3.org/1998/Math/MathML">a■b{displaystyle a prendab} | |||
| b}" xmlns="http://www.w3.org/1998/Math/MathML">a■b{displaystyle a prendab} | a=b{displaystyle a=b} | |||||
| Triclínico primitivo | a→ → i⋅ ⋅ a→ → jل ل 0{displaystyle {vec {a}_{i}cdot {fnK} {fnMicrosoft}fnK} 0} i,j▪ ▪ {}1,2,3,4}{displaystyle i,jin {1,2,3,4} Donde iل ل j{displaystyle ineq j} | a→ → i⋅ ⋅ a→ → j=0{displaystyle {vec {a}_{i}cdot {fnK}=0} una vez | a→ → i⋅ ⋅ a→ → j=0=a→ → k⋅ ⋅ a→ → l{displaystyle {vec {fnK}cdot {fnMic} {a}_{j}=0={vec} {fnK}cdot {fnMic} {a}_{l} i,j,k,l▪ ▪ {}1,2,3,4}{displaystyle i,j,k,lin {1,2,3,4} Donde iل ل jل ل kل ل l{displaystyle ineq jneq kneq l} | |||
Trajes compuestos
Para redes compuestas (cristales que tienen más de un vector en su base), cada punto de la red representa múltiples átomos. Podemos dividir cada celda de Wigner-Seitz en subceldas mediante una mayor descomposición de Voronoi según el átomo más cercano, en lugar del punto de red más cercano. Por ejemplo, la estructura cristalina del diamante contiene una base de dos átomos. En el diamante, los átomos de carbono tienen enlaces tetraédricos sp3, pero dado que los tetraedros no ocupan el espacio, la descomposición de voronoi de la estructura cristalina del diamante es en realidad el panal tetraédrico truncado de triakis. Otro ejemplo es la aplicación de la descomposición de Voronoi a los átomos en las fases A15, que forma la aproximación poliédrica de la estructura Weaire-Phelan.
Simetría
La celda de Wigner-Seitz siempre tiene la misma simetría puntual que la red de Bravais subyacente. Por ejemplo, el cubo, el octaedro truncado y el dodecaedro rómbico tienen simetría puntual Oh, ya que las respectivas redes de Bravais utilizadas para generarlos pertenecen al sistema de red cúbica, que tiene Oh punto de simetría.
Zona Brillouin
En la práctica, la celda de Wigner-Seitz en sí rara vez se usa como descripción del espacio directo, donde generalmente se usan las celdas unitarias convencionales. Sin embargo, la misma descomposición es extremadamente importante cuando se aplica al espacio recíproco. La celda de Wigner-Seitz en el espacio recíproco se llama zona de Brillouin y contiene información sobre si un material será conductor, semiconductor o aislante.
Contenido relacionado
Julio (unidad)
Pascal (unidad)
Conjunto vacío

















