Celosía de Bravais

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Conjunto de puntos de geometría y cristalografía

En geometría y cristalografía, una red de Bravais, llamada así en honor a Auguste Bravais (1850), es una matriz infinita de puntos discretos generados por un conjunto de operaciones de traducción discretas descritas en un espacio tridimensional por

{displaystyle mathbf {R} =n_{1}mathbf {a} _{1}+n_{2}mathbf {a} _{2}+n_{3}mathbf {a} _{3},}

donde n_i son números enteros y a_i son vectores de traducción primitivos, o vectores primitivos, que se encuentran en diferentes direcciones (no necesariamente mutuamente perpendiculares) y abarcan la red. La elección de vectores primitivos para una determinada red de Bravais no es única. Un aspecto fundamental de cualquier red de Bravais es que, para cualquier elección de dirección, la red parece exactamente igual desde cada uno de los puntos discretos de la red cuando se mira en esa dirección elegida.

El concepto de red de Bravais se utiliza para definir formalmente una disposición cristalina y sus fronteras (finitas). Un cristal está formado por uno o más átomos, llamados base o motivo, en cada punto de la red. La base puede consistir en átomos, moléculas o cadenas de polímeros de materia sólida, y la red proporciona las ubicaciones de la base.

Dos redes de Bravais a menudo se consideran equivalentes si tienen grupos de simetría isomórficos. En este sentido, hay 5 posibles redes de Bravais en un espacio bidimensional y 14 posibles redes de Bravais en un espacio tridimensional. Los 14 posibles grupos de simetría de las redes de Bravais son 14 de los 230 grupos espaciales. En el contexto de la clasificación de grupos espaciales, las redes de Bravais también se denominan clases de Bravais, clases aritméticas de Bravais o bandadas de Bravais.

Unidad celular

En la cristalografía, existe el concepto de una célula unitaria que comprende el espacio entre puntos de celo adyacentes y cualquier átomo en ese espacio. Una célula unidad se define como un espacio que, cuando se traduce a través de un subconjunto de todos los vectores descritos por ${displaystyle mathbf {R} =n_{1}mathbf {a} _{1}+n_{2}mathbf {a} _{2}+n_{3}mathbf {a} _{3}}$ , llena el espacio de celosía sin superposición o vacíos. (Es decir, un espacio de celo es un múltiplo de una célula unidad.) Hay principalmente dos tipos de células unitarias: células de unidad primitivas y células de unidad convencionales. Una célula primitiva es el componente más pequeño de una celosía (o cristal) que, al apilarse junto con operaciones de traducción de celosía, reproduce toda la celosía (o cristal). Tenga en cuenta que las traducciones deben ser operaciones de traducción de celos que hacen que la celosía aparezca sin cambios después de la traducción. Si se permiten traducciones arbitrarias, uno podría hacer una célula primitiva la mitad del tamaño de la verdadera, y traducir dos veces más a menudo, como ejemplo. Otra manera de definir el tamaño de una célula primitiva que evita invocar las operaciones de traducción de celosía, es decir que la célula primitiva es el componente más pequeño posible de una celosía (o cristal) que se puede repetir para reproducir toda la celosía (o cristal), y que contiene exactamente un punto de celo. En cualquier definición, la célula primitiva se caracteriza por su pequeño tamaño. Hay claramente muchas opciones de la célula que pueden reproducir toda la celosía cuando se apilan (dos mitades de celo, por ejemplo), y el requisito de tamaño mínimo distingue la célula primitiva de todas estas otras unidades de repetición válidas. Si la celosía o el cristal es de 2 dimensiones, la célula primitiva tiene un área mínima; igualmente en 3 dimensiones la célula primitiva tiene un volumen mínimo. A pesar de este rígido requisito de tamaño mínimo, no hay una opción única de célula unidad primitiva. De hecho, todas las células cuyas fronteras son vectores de traducción primitiva serán células de unidad primitiva. El hecho de que no haya una elección única de vectores de traducción primitiva para una determinada celosía conduce a la multiplicidad de posibles células de unidad primitiva. Las células unitarias convencionales, por otro lado, no son necesariamente células de tamaño mínimo. Son elegidos puramente para comodidad y a menudo se utilizan para fines de ilustración. Se definen libremente.

Las celdas unitarias primitivas se definen como celdas unitarias con el volumen más pequeño para un cristal determinado. (Un cristal es una red y una base en cada punto de la red). Para tener el volumen de celda más pequeño, una celda unitaria primitiva debe contener (1) sólo un punto de la red y (2) la cantidad mínima de constituyentes básicos (por ejemplo, la cantidad mínima de constituyentes básicos). número de átomos en una base). Para el primer requisito, contar el número de puntos de la red en una celda unitaria es tal que, si un punto de la red es compartido por m celdas unitarias adyacentes alrededor de ese punto de la red, entonces el punto se cuenta como 1/ soy. Este último requisito es necesario ya que hay cristales que pueden describirse mediante más de una combinación de red y base. Por ejemplo, un cristal, visto como una red con un solo tipo de átomo ubicado en cada punto de la red (la forma básica más simple), también puede verse como una red con una base de dos átomos. En este caso, una celda unitaria primitiva es una celda unitaria que tiene solo un punto de red en la primera forma de describir el cristal para garantizar el volumen de celda unitaria más pequeño.

Puede haber más de una forma de elegir una celda primitiva para un cristal determinado y cada elección tendrá una forma de celda primitiva diferente, pero el volumen de la celda primitiva es el mismo para cada elección y cada elección tendrá la propiedad de que Se puede establecer una correspondencia uno a uno entre celdas unitarias primitivas y puntos de red discretos sobre la red asociada. Todas las celdas unitarias primitivas con diferentes formas para un cristal determinado tienen el mismo volumen por definición; Para un cristal dado, si n es la densidad de los puntos de la red en una red que garantiza la cantidad mínima de constituyentes básicos y v es el volumen de una celda primitiva elegida, entonces nv = 1, lo que da como resultado v = 1/n, por lo que cada celda primitiva tiene el mismo volumen de 1/n .

Entre todas las células primitivas posibles para un cristal dado, una célula primitiva obvia puede ser el paralelepípedo formado por un conjunto elegido de vectores de traducción primitiva. (De nuevo, estos vectores deben hacer una celosía con la cantidad mínima de constituyentes de base.) Es decir, el conjunto de todos los puntos ${displaystyle mathbf {r} =x_{1}mathbf {a} _{1}+x_{2}mathbf {a} _{2}+x_{3}mathbf {a} _{3}}$ Donde $<math alttext="{displaystyle 0leq x_{i}0≤ ≤ xic)1{displaystyle 0leq x_{i}traducido1}<img alt="{displaystyle 0leq x_{i}$ y ${displaystyle mathbf {a} _{i}}$ es el vector primitivo elegido. Esta célula primitiva no siempre muestra la simetría clara de un cristal dado. En este caso, a menudo se utiliza una célula unidad convencional que muestra fácilmente la simetría de cristal. El volumen de la célula unidad convencional será un integer-multiple del volumen de la célula unidad primitiva.

Origen del concepto

En dos dimensiones, cualquier red puede especificarse por la longitud de sus dos vectores de traslación primitivos y el ángulo entre ellos. Hay un número infinito de redes posibles que se pueden describir de esta manera. Se desea alguna forma de categorizar diferentes tipos de celosías. Una forma de hacerlo es reconocer que algunas redes tienen simetría inherente. Se pueden imponer condiciones sobre la longitud de los vectores de traducción primitivos y sobre el ángulo entre ellos para producir varias redes simétricas. Estas simetrías en sí mismas se clasifican en diferentes tipos, como grupos de puntos (que incluyen simetrías especulares, simetrías de inversión y simetrías de rotación) y simetrías traslacionales. Por lo tanto, las celosías se pueden clasificar según el grupo de puntos o la simetría traslacional que se les aplica.

En dos dimensiones, el grupo de puntos más básico corresponde a la invariancia rotacional bajo 2π y π, o simetría rotacional 1 y 2. En realidad, esto se aplica automáticamente a todas las redes 2D y es el grupo de puntos más general. Las redes contenidas en este grupo (técnicamente todas las redes, pero convencionalmente todas las redes que no caen en ninguno de los otros grupos de puntos) se denominan redes oblicuas. A partir de ahí, hay 4 combinaciones adicionales de grupos de puntos con elementos de traslación (o equivalentemente, 4 tipos de restricción en las longitudes/ángulos de los vectores de traslación primitivos) que corresponden a las 4 categorías de red restantes: cuadrado, hexagonal, rectangular y centrado. rectangular. Por tanto, en total hay 5 celosías de Bravais en 2 dimensiones.

Asimismo, en 3 dimensiones, existen 14 celosías de Bravais: 1 "papelera" categoría (triclínica) y 13 categorías más. Estos 14 tipos de redes se clasifican por sus grupos de puntos en 7 sistemas de redes (triclínico, monoclínico, ortorrómbico, tetragonal, cúbico, romboédrico y hexagonal).

En 2 dimensiones

En el espacio bidimensional hay 5 redes de Bravais, agrupadas en cuatro sistemas de redes, como se muestra en la siguiente tabla. Debajo de cada diagrama está el símbolo de Pearson para esa red de Bravais.

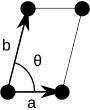
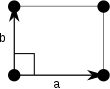
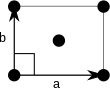
Nota: En los diagramas de celdas unitarias de la siguiente tabla, los puntos de la red se representan mediante círculos negros y las celdas unitarias se representan mediante paralelogramos (que pueden ser cuadrados o rectángulos) delineados en negro. Aunque cada una de las cuatro esquinas de cada paralelogramo se conecta a un punto de la red, técnicamente sólo uno de los cuatro puntos de la red pertenece a una celda unitaria determinada y cada uno de los otros tres puntos de la red pertenece a una de las celdas unitarias adyacentes. Esto se puede ver imaginando mover el paralelogramo de celda unitaria ligeramente hacia la izquierda y ligeramente hacia abajo mientras se dejan fijos todos los círculos negros de los puntos de la red.

Sistema de celos	Grupo de puntos (Notación de Schönflies)	5 Lattices de Bravais
Sistema de celos	Grupo de puntos (Notación de Schönflies)	Primitivo p)	Centered (c)
Monoclinica m)	C₂	Oblicua (mp)
Orthorhombic (o)	D₂	Rectangular (op)	Centro rectangular (oc)
Tetragonal (t)	D₄	Plaza (tp)
Hexagonal (h)	D₆	Hexagonal (hp)

Las celdas unitarias se especifican según las longitudes relativas de los bordes de las celdas (a y b) y el ángulo entre ellos (θ ). El área de la celda unitaria se puede calcular evaluando la norma ‖a × b‖, donde a y b son los vectores reticulares. Las propiedades de los sistemas reticulares se dan a continuación:

Sistema de celos	Zona	Distancias axiales (longitudes de borde)	Ángulo axial
Monoclinic	${displaystyle ab,sin theta }$
Orthorhombic	${displaystyle ab}$		Silencio = 90°
Tetragonal	${displaystyle a^{2}}$	a = b	Silencio = 90°
Hexagonal	${displaystyle {frac {sqrt {3}}{2}},a^{2}}$	a = b	Silencio = 120°

En 3 dimensiones

En el espacio tridimensional hay 14 redes de Bravais. Estos se obtienen combinando uno de los siete sistemas de celosía con uno de los tipos de centrado. Los tipos de centrado identifican las ubicaciones de los puntos de la red en la celda unitaria de la siguiente manera:

Primitivo (P): puntos de celo en las esquinas de las celdas solamente (a veces llamado simple)
Base-centrada (S: A, B, o C): puntos de celo en las esquinas de las celdas con un punto adicional en el centro de cada cara de un par de caras paralelas de la célula (a veces llamado centrado en el extremo)
Cuerpo-centrado (I): puntos de celo en las esquinas celulares, con un punto adicional en el centro de la célula
Face-centered (F): puntos de celo en las esquinas celulares, con un punto adicional en el centro de cada una de las caras de la célula

No todas las combinaciones de sistemas reticulares y tipos de centrado son necesarias para describir todas las retículas posibles, ya que se puede demostrar que varias de ellas son, de hecho, equivalentes entre sí. Por ejemplo, la red monoclínica I puede describirse como una red monoclínica C mediante una elección diferente de ejes cristalinos. De manera similar, todas las redes centradas en A o B pueden describirse mediante un centrado en C o en P. Esto reduce el número de combinaciones a 14 celosías Bravais convencionales, como se muestra en la siguiente tabla. Debajo de cada diagrama está el símbolo de Pearson para esa red de Bravais.

Nota: En los diagramas de celda unitaria de la siguiente tabla se muestran todos los puntos de la red en el límite de la celda (esquinas y caras); sin embargo, no todos estos puntos de la red pertenecen técnicamente a la celda unitaria dada. Esto se puede ver imaginando mover la celda unitaria ligeramente en la dirección negativa de cada eje mientras se mantienen fijos los puntos de la red. En términos generales, esto se puede considerar como mover la celda unitaria ligeramente hacia la izquierda, ligeramente hacia abajo y ligeramente fuera de la pantalla. Esto muestra que solo uno de los ocho puntos de la red de las esquinas (específicamente el frontal, izquierdo, inferior) pertenece a la celda unitaria dada (los otros siete puntos de la red pertenecen a celdas unitarias adyacentes). Además, sólo uno de los dos puntos de la red que se muestran en las caras superior e inferior de la columna Centrada en la base pertenece a la celda unitaria dada. Finalmente, sólo tres de los seis puntos de la red en las caras de la columna Centrado en la cara pertenecen a la celda unitaria dada.

Familia de cristal	Sistema de celos	Grupo de puntos (Notación de Schönflies)	14 Bravais lattices
Familia de cristal	Sistema de celos	Grupo de puntos (Notación de Schönflies)	Primitivo (P)	Base centrada (S)	Cuerpo centrado (I)	Face-centered (F)
Triclinic (a)		C_i	aP
Monoclinica m)		C_2h	mP	mS
Orthorhombic (o)		D_2h	oP	OS	o I	oF
Tetragonal (t)		D_4h	tP		tI
Hexagonal (h)	Rimboedral	D_3d	hR
Hexagonal (h)	Hexagonal	D_6h	hP
Cubic (c)		O_h	cP		cI	cF

Las celdas unitarias se especifican de acuerdo con seis parámetros de red que son las longitudes relativas de los bordes de las celdas (a, b, c) y los ángulos entre ellos (α, β, γ), donde α es el ángulo entre b y c, β es el ángulo entre a y c, y γ es el ángulo entre a y b. El volumen de la celda unitaria se puede calcular evaluando el producto triple a · (b × c) , donde a, b y c son los vectores reticulares. Las propiedades de los sistemas reticulares se dan a continuación:

Familia de cristal	Sistema de celos	Volumen	Distancias axiales (longitudes de borde)	Ángulos axiales	Ejemplos de correspondencia
Triclinic		${displaystyle abc{sqrt {1-cos ^{2}alpha -cos ^{2}beta -cos ^{2}gamma +2cos alpha cos beta cos gamma }}}$			K2Cr2O7, CuSO4·5H2O, H3BO3
Monoclinic		${displaystyle abc,sin beta }$		α = γ = 90°	Azufre monoclínico, Na2SO4·10H2O, PbCrO3
Orthorhombic		${displaystyle abc}$		α = β = γ = 90°	Azufre Rhombic, KNO3, BaSO4
Tetragonal		${displaystyle a^{2}c}$	a = b	α = β = γ = 90°	Lata blanca, SnO2, TiO2, CaSO4
Hexagonal	Rimboedral	${displaystyle a^{3}{sqrt {1-3cos ^{2}alpha +2cos ^{3}alpha }}}$	a = b = c	α = β = γ	Calcite (CaCO₃), canilla (HgS)
Hexagonal	Hexagonal	${displaystyle {frac {sqrt {3}}{2}},a^{2}c}$	a = b	α = β = 90°, γ = 120°	Grafito, ZnO, CdS
Cubic		${displaystyle a^{3}}$	a = b = c	α = β = γ = 90°	NaCl, mezcla de zinc, metal de cobre, KCl, Diamantes, Plata

Alguna información básica para los sistemas de celosías y celosías de Bravais en tres dimensiones se resume en el diagrama al principio de esta página. El polígono de siete lados (heptágono) y el número 7 en el centro indican los siete sistemas reticulares. Los heptágonos internos indican los ángulos de la red, los parámetros de la red, las redes de Bravais y las notaciones de Schöenflies para los respectivos sistemas de redes.

En 4 dimensiones

En cuatro dimensiones, hay 64 redes de Bravais. De ellos, 23 son primitivos y 41 están centrados. Diez redes de Bravais se dividen en pares enantiomórficos.

Contenido relacionado

Más resultados...