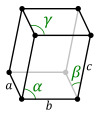
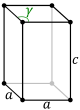
Celda unitaria

En geometría, biología, mineralogía y física del estado sólido, una celda unitaria es una unidad repetitiva formada por los vectores que abarcan los puntos de una red. A pesar de su sugerente nombre, la celda unitaria (a diferencia de un vector unitario, por ejemplo) no tiene necesariamente un tamaño unitario, ni siquiera un tamaño particular. Más bien, la celda primitiva es la analogía más cercana a un vector unitario, ya que tiene un tamaño determinado para una red dada y es el componente básico a partir del cual se construyen las celdas más grandes.

El concepto se usa particularmente para describir la estructura cristalina en dos y tres dimensiones, aunque tiene sentido en todas las dimensiones. Una red se puede caracterizar por la geometría de su celda unitaria, que es una sección del mosaico (un paralelogramo o un paralelepípedo) que genera todo el mosaico usando solo traslaciones.

Hay dos casos especiales de celda unitaria: la celda primitiva y la celda convencional. La celda primitiva es una celda unitaria correspondiente a un solo punto de red, es la celda unitaria más pequeña posible. En algunos casos, la simetría completa de una estructura cristalina no es obvia desde la celda primitiva, en cuyo caso se puede usar una celda convencional. Una celda convencional (que puede ser primitiva o no) es una celda unitaria con la simetría completa de la red y puede incluir más de un punto de red. Las celdas unitarias convencionales son paralelotopos en n dimensiones.

Célula primitiva

Una celda primitiva es una celda unitaria que contiene exactamente un punto reticular. En general, para las celdas unitarias, los puntos de red que comparten las celdas n se cuentan como 1/n de los puntos de red contenidos en cada una de esas celdas; así, por ejemplo, se considera que una celda unitaria primitiva en tres dimensiones que tiene puntos reticulares solo en sus ocho vértices contiene 1 /8 de cada uno de ellos. Una conceptualización alternativa es elegir consistentemente solo uno de los n puntos reticulares para que pertenezcan a la celda unitaria dada (por lo que los otros n-1 los puntos de red pertenecen a celdas unitarias adyacentes).

Los vectores de traducción primitivos a→₁, a→₂, a→₃ abarcan una celda de red de volumen más pequeño para una red tridimensional particular, y se utilizan para definir un vector de traducción de cristal

T→ → =u1a→ → 1+u2a→ → 2+u3a→ → 3,{displaystyle {vec}=u_{1}{vec} {fn} {fnK} {fnMicrosoft} {fnMicrosoft}} {fn}}} {fn}} {fn}} {fn}}}} {fn}fnfn}}}\fnfn}f}}fnfnf}}}}\\fn}}}\\\\\\\\\\fn}fn}}}}}}}}}}}\\\\\\\\\\\\\\\fn}}}}}}}}}}}}}}}\\\\\\\\\\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fn}}} {fn}}}} {fn}}}} {fn}}}}} {fnfn}}}}\\fn}}fn}}}\\fn}}}}}\\fn}}}}}}}}}}}}\\\\\\\\c}}}}}}}}}}}\\\\\\\\\\c}}}}}}}}\\\\\\\\\\c}}}}}}}}}}}}}\\\\\\\\\\c}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {a}_{3},}

donde u₁, u₂, u₃ son números enteros, cuya traducción deja la red invariable. Es decir, para un punto en la red r, la disposición de los puntos parece la misma desde r ′ = r + T→ a partir de r.

Dado que la celda primitiva está definida por los ejes primitivos (vectores) a→₁, a→₂, a→₃, el volumen V _p de la celda primitiva está dada por el paralelepípedo de los ejes anteriores como

Vp=Silencioa→ → 1⋅ ⋅ ()a→ → 2× × a→ → 3)Silencio.{displaystyle V_{mathrm}=left forever{vec} {a}_{1}cdot ({vec {a}_{2}times {vec {}_{3})right sobre la vida.}

Por lo general, las celdas primitivas en dos y tres dimensiones se eligen para tomar la forma de paralelogramos y paralelepípedos, con un átomo en cada esquina de la celda. Esta elección de celda primitiva no es única, pero el volumen de celdas primitivas siempre estará dado por la expresión anterior.

Célula de Wigner-Seitz

Además de las celdas primitivas paralelepipédicas, por cada red de Bravais existe otro tipo de celda primitiva llamada celda de Wigner-Seitz. En la celda de Wigner-Seitz, el punto de la red está en el centro de la celda y, para la mayoría de las redes de Bravais, la forma no es un paralelogramo o un paralelepípedo. Este es un tipo de célula de Voronoi. La celda de Wigner-Seitz de la red recíproca en el espacio de momento se denomina zona de Brillouin.

Célula convencional

Para cada red en particular, los cristalógrafos han elegido una celda convencional caso por caso en función de la conveniencia del cálculo. Estas celdas convencionales pueden tener puntos de celosía adicionales ubicados en el medio de las caras o el cuerpo de la celda unitaria. El número de puntos de la red, así como el volumen de la celda convencional, es un múltiplo entero (1, 2, 3 o 4) del de la celda primitiva.

Dos dimensiones

El paralelograma es la célula primitiva general para el avión.

Para cualquier red bidimensional, las celdas unitarias son paralelogramos, que en casos especiales pueden tener ángulos ortogonales, longitudes iguales o ambos. Cuatro de las cinco redes de Bravais bidimensionales se representan utilizando celdas primitivas convencionales, como se muestra a continuación.

Celda primitiva convencional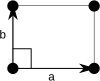
Nombre de la forma	Parallelograma	Rectángulo	Plaza	Rhombus
Bravais lattice	Oblicua primitiva	Primitive Rectangular	Plaza primitiva	Primitive Hexagonal

La red rectangular centrada también tiene una celda primitiva en forma de rombo, pero para permitir una fácil discriminación sobre la base de la simetría, se representa mediante una celda convencional que contiene dos puntos de red.

Celda primitiva
Nombre de la forma	Rhombus
Celda convencional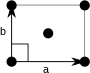
Bravais lattice	Centered Rectangular

Tres dimensiones

Un paralelo es una célula primitiva general para el espacio tridimensional.

Para cualquier red tridimensional, las celdas unitarias convencionales son paralelepípedos, que en casos especiales pueden tener ángulos ortogonales, longitudes iguales o ambos. Siete de los catorce retículos tridimensionales de Bravais se representan utilizando celdas primitivas convencionales, como se muestra a continuación.

Celda primitiva convencional
Nombre de la forma	Parallelepiped	Prisma rectangular oblicua	Cuboide rectangular	Cuboide cuadrado	Trigonal trapezohedron	Cube	Derecho prisma rhombic
Bravais lattice	Primitive Triclinic	Monoclinico primitivo	Orthorhombic primitivo	Tetragonal primitivo	Primitive Rhombohedral	Primitive Cubic	Primitive Hexagonal

Los otros siete retículos de Bravais (conocidos como retículos centrados) también tienen celdas primitivas en forma de paralelepípedo, pero para permitir una fácil discriminación sobre la base de la simetría, están representados por celdas convencionales que contienen más de un punto de celosía.

Celda primitiva
Nombre de la forma	prisma romábico oblicua	Derecho prisma rhombic
Celda convencional
Bravais lattice	Monoclinico centrado en la base	Orthorhombic centrado en la base	Orthorhombic centrado en el cuerpo	Orthorhombic centrado en la cara	Tetragonal centrado en el cuerpo	Cubic centrado en el cuerpo	Cubic centrado en la cara