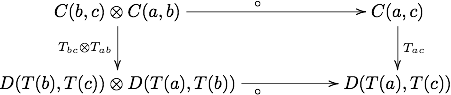Categoría enriquecida

En la teoría de categorías, una rama de las matemáticas, una categoría enriquecida generaliza la idea de una categoría al reemplazar los conjuntos de hom- bres con objetos de una categoría monoidal general. Está motivado por la observación de que, en muchas aplicaciones prácticas, el hom-set a menudo tiene una estructura adicional que debe respetarse, por ejemplo, la de ser un espacio vectorial de morfismos o un espacio topológico de morfismos. En una categoría enriquecida, el conjunto de morfismos (el conjunto hom) asociado con cada par de objetos se reemplaza por un objeto en alguna categoría monoidal fija de "objetos hom". Para emular la composición (asociativa) de los morfismos en una categoría ordinaria, la categoría-hom debe tener un medio para componer objetos-hom de manera asociativa: es decir, debe haber una operación binaria sobre los objetos que nos proporcione al menos la estructura de una categoría monoide, aunque en algunos contextos la operación también puede necesitar ser conmutativa y quizás también tener un adjunto derecho (es decir, hacer que la categoría sea monoide simétrica o incluso monoidal cerrada simétrica, respectivamente).

La teoría de categorías enriquecidas abarca, por lo tanto, dentro del mismo marco, una amplia variedad de estructuras que incluyen

• categorías ordinarias donde el hom-set lleva estructura adicional más allá de ser un conjunto. Es decir, hay operaciones en, o propiedades de morfismos que necesitan ser respetados por la composición (por ejemplo, la existencia de 2 células entre morfismos y composición horizontal de ellos en una 2-categoría, o la operación adicional sobre morfismos en una categoría abeliana)
• entidades de categoría-como que no tienen ninguna noción de morfismo individual pero cuyos hom-objetos tienen aspectos compositivos similares (por ejemplo, preordens donde la regla de composición asegura transitividad, o los espacios métricos de Lawvere, donde los hom-objetos son distancias numéricas y la regla de composición proporciona la desigualdad triángulo).

En el caso de que la categoría hom-objeto resulte ser la categoría de conjuntos con el producto cartesiano habitual, las definiciones de categoría enriquecida, funtor enriquecido, etc... se reducen a las definiciones originales de la teoría de categorías ordinarias.

Se dice que una categoría enriquecida con hom-objetos de la categoría monooidal M es una categoría enriquecida sobre M o una categoría enriquecida en M, o simplemente una categoría M. Debido a la preferencia de Mac Lane por la letra V al referirse a la categoría monoide, las categorías enriquecidas a veces también se denominan generalmente categorías V.

Definición

Sea (M, ⊗, I, α, λ, ρ) sea una categoría monoide. Luego, una categoría enriquecida C (alternativamente, en situaciones en las que la elección de la categoría monoide debe ser explícita, una categoría enriquecida sobre M , o M-categoría), consta de

• una clase ob()C) de objetos de C,
• un objeto C()a, b) de M para cada par de objetos a, b dentro C, utilizado para definir una flecha f:a→ → b{displaystyle f:arightarrow b) dentro C como una flecha f:I→ → C()a,b){displaystyle f:Irightarrow C(a,b)} dentro M,
• una flecha id_a: I → C()a, a) dentro M designando un identidad para cada objeto a dentro C, y
• una flecha °_abc: C()b, c⊗ C()a, b) → C()a, c) dentro M designando un composición para cada triple de objetos a, b, c dentro C, utilizado para definir la composición f:a→ → b{displaystyle f:arightarrow b) y g:b→ → c{displaystyle g:brightarrow c} dentro C como g∘ ∘ Cf=∘ ∘ abc()g⊗ ⊗ f){displaystyle gcirc _{textbf {C}f={circ }_{abc}(gotimes f)} junto con tres diagramas de conmutación, discutidos a continuación.

El primer diagrama expresa la asociatividad de la composición:

Es decir, el requisito de asociatividad ahora lo asume el asociador de la categoría monoide M.

Para el caso de que M sea la categoría de conjuntos y (⊗, I, α, λ, ρ) es la estructura monoide (×, {•}, …) dada por el producto cartesiano, el conjunto terminal de un solo punto y los isomorfismos canónicos que inducen, entonces cada C(a, b) es un conjunto cuyos elementos pueden considerarse como "morfismos individuales" de C, mientras que °, ahora una función, define cómo se componen los morfismos consecutivos. En este caso, cada ruta que conduce a C(a, d) en la primera corresponde a una de las dos formas de componer tres morfismos individuales consecutivos a → b → c → d, es decir, elementos de C(a, b) , C(b, c) y C(c, d). La conmutatividad del diagrama es entonces meramente la declaración de que ambos órdenes de composición dan el mismo resultado, exactamente como se requiere para las categorías ordinarias.

Lo que es nuevo aquí es que lo anterior expresa el requisito de asociatividad sin ninguna referencia explícita a los morfismos individuales en la categoría enriquecida C — nuevamente, estos diagramas son para morfismos en la categoría monoide M , y no en C, lo que hace que el concepto de asociatividad de la composición sea significativo en el caso general en el que los hom-objetos C(a, b) son abstractos, y C ni siquiera necesita tener ninguna noción del morfismo individual.

La noción de que una categoría ordinaria debe tener morfismos de identidad se reemplaza por los diagramas segundo y tercero, que expresan la identidad en términos de unitores izquierdo y derecho:

y

Volviendo al caso donde M es la categoría de conjuntos con producto cartesiano, los morfismos id_a: I → C(a, a) se convierten en funciones del conjunto de un punto I y debo entonces, para cualquier objeto dado a, identificar un elemento particular de cada conjunto C(a, a), algo que podemos considerar como el "morfismo de identidad para a en C ". La conmutatividad de los dos últimos diagramas es entonces la afirmación de que las composiciones (según lo definido por las funciones °) que involucran estos "morfismos de identidad individuales distinguidos en C" comportarse exactamente según las reglas de identidad para las categorías ordinarias.

Tenga en cuenta que hay varias nociones distintas de "identidad" siendo referenciado aquí:

• el objeto monoidal de identidad I de M, siendo una identidad para ⊗ sólo en el sentido monoide-teorético, e incluso entonces sólo hasta el isomorfismo canónico ()λ, ***).
• el Morfismo de identidad 1_{C()a, b)}: C()a, b) → C()a, b) que M tiene para cada uno de sus objetos por ser (al menos) una categoría ordinaria.
• el identidad enriquecida id_a: I → C()a, a) para cada objeto a dentro C, que es otra vez un morfismo M que, incluso en el caso C es considerados que tienen morfismos individuales propios, no es necesariamente identificar uno específico.

Ejemplos de categorías enriquecidas

• Las categorías ordinarias son categorías enriquecidas (Set, ×, {•}), la categoría de conjuntos con el producto cartesiano como la operación monoidal, como se señaló anteriormente.
• 2-Categorías son categorías enriquecidas Gato, la categoría de pequeñas categorías, con estructura monoidal que se da por el producto cartesiano. En este caso las 2 células entre morfismos a → b y la regla de la composición vertical que los relaciona corresponde a los morfismos de la categoría ordinaria C()a,b) y su propia regla de composición.
• Las categorías localmente pequeñas son categorías enriquecidas (SmSet, ×), la categoría de pequeños conjuntos con el producto cartesiano como la operación monoidal. (Una categoría localmente pequeña es uno cuyos hom-objetos son pequeños conjuntos.)
• Las categorías localmente finitas, por analogía, son categorías enriquecidas (FinSet, ×), la categoría de conjuntos finitos con el producto cartesiano como la operación monoidal.
• Si C es una categoría monoidal cerrada entonces C se enriquece en sí mismo.
• Los juegos preordenados son categorías enriquecidas sobre una determinada categoría monoidal, 2, que consiste en dos objetos y una sola flecha de no identidad entre ellos que podemos escribir como FALSE → TRUE, conjunción como la operación monoide, y TRUE como su identidad monoidal. Los hom-objetos 2()a,b) entonces simplemente negar o afirmar una relación binaria particular en el par dado de objetos (a,b); por el bien de tener notación más familiar podemos escribir esta relación como a ≤ b. La existencia de las composiciones e identidades necesarias para una categoría enriquecida sobre 2 traducir inmediatamente a los siguientes axiomas respectivamente

b ≤ c y a ≤ b ⇒ a ≤ c (transitividad)

TRUE ⇒ a ≤ a (reflexividad)

que no son más que los axiomas por ser un preorden. Y desde todos los diagramas en 2 Comute, este es el sole contenido de los axiomas de la categoría enriquecida para categorías enriquecidas 2.

• Los espacios métricos generalizados de William Lawvere, también conocidos como espacios pseudoquasimétricos, son categorías enriquecidas sobre los números reales no negativos extendidos R⁺, donde se le da la estructura de categoría ordinaria a través de la inversa de su orden habitual (es decir, existe un morfismo r → s Sip r ≥ s) y una estructura monoidal mediante adición (+) y cero (0). Los hom-objetos R⁺()a, b) son esencialmente distancias d(a,b), y la existencia de composición e identidad se traduce a

d(b,c) + d(a,b) ≥ d(a,c) (triángulo desigualdad)

0 ≥ d(a,a)

• Categorías con cero morfismos son categorías enriquecidas (Conjunto*, ∧), la categoría de conjuntos puntiagudos con producto destrozado como la operación monoidal; el punto especial de un hom-object Hom(A,B) corresponde al morfismo cero de A a B.
• La categoría Ab de los grupos abelianos y la categoría R-Mod de módulos sobre un anillo conmutativo, y la categoría Vect de espacios vectoriales sobre un campo dado se enriquecen sobre sí mismos, donde los morfismos heredan la estructura algebraica "puntura". En términos más generales, las categorías preadditivas se enriquecen (en inglés)Ab, ⊗) con el producto tensor como la operación monoidal (pensando grupos abelianos como Z-módulos).

Relación con funtores monoidales

Si hay un funtor monoide de una categoría monoidal M a una categoría monoide N, entonces cualquier categoría enriquecida sobre M puede reinterpretarse como categoría enriquecida sobre N. Toda categoría monoide M tiene un funtor monoide M(I, –) a la categoría de conjuntos, por lo que cualquier categoría enriquecida tiene una categoría ordinaria subyacente. En muchos ejemplos (como los anteriores), este funtor es fiel, por lo que una categoría enriquecida sobre M puede describirse como una categoría ordinaria con cierta estructura o propiedades adicionales.

Funtores enriquecidos

Un funtor enriquecido es la generalización apropiada de la noción de funtor a categorías enriquecidas. Los funtores enriquecidos son entonces mapas entre categorías enriquecidas que respetan la estructura enriquecida.

Si C y D son categorías M (es decir, categorías enriquecidas sobre la categoría monoide M), un funtor enriquecido con M T: C → D es un mapa que asigna a cada objeto de C un objeto de D y para cada par de objetos a y b en C proporciona un morfismo en M T_ab: C(a, b ) → D(T(a), T(b)) entre los hom-objetos de C y D (que son objetos en M), satisfaciendo versiones enriquecidas de los axiomas de un funtor, a saber, la preservación de la identidad y la composición.

Debido a que los hom-objetos no necesitan ser conjuntos en una categoría enriquecida, no se puede hablar de un morfismo particular. Ya no existe la noción de un morfismo de identidad, ni de una composición particular de dos morfismos. En cambio, los morfismos de la unidad a un hom-objeto se deben considerar como la selección de una identidad, y los morfismos del producto monoide se deben considerar como una composición. Los axiomas funcionales habituales se reemplazan con los diagramas conmutativos correspondientes que involucran estos morfismos.

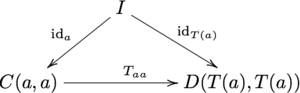
En detalle, se tiene que el diagrama

conmuta, lo que equivale a la ecuación

Taa∘ ∘ ida=idT()a),{displaystyle T_{aa}circ operatorname {id} ¿Qué?

donde I es el objeto unitario de M. Esto es análogo a la regla F(id_a) = id_{F(a )} para funtores ordinarios. Además, se exige que el diagrama

conmutar, que es análogo a la regla F(fg)=F(f)F(g) para funtores ordinarios.