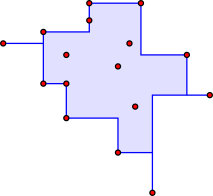
Casco convexo

Compartir Imprimir Citar

Convexo más pequeño que contiene un conjunto dado

El casco convexo del conjunto rojo es el conjunto de convexo azul y rojo.

En geometría, el casco convexo o envoltura convexa o cierre convexo de una forma es el conjunto convexo más pequeño que la contiene. La envolvente convexa se puede definir como la intersección de todos los conjuntos convexos que contienen un subconjunto dado de un espacio euclidiano o, de manera equivalente, como el conjunto de todas las combinaciones convexas de puntos en el subconjunto. Para un subconjunto acotado del avión, el casco convexo se puede visualizar como la forma encerrada por una banda elástica estirada alrededor del subconjunto.

Los cascos convexos de conjuntos abiertos están abiertos, y los cascos convexos de conjuntos compactos son compactos. Cada conjunto convexo compacto es el casco convexo de sus puntos extremos. El operador de casco convex es un ejemplo de un operador de cierre, y todos los antimatroides pueden ser representados aplicando este operador de cierre a conjuntos finitos de puntos. Los problemas algorítmicos de encontrar el casco convexo de un conjunto finito de puntos en el plano u otros espacios euclidianos de baja dimensión, y su doble problema de intersección de medio espacio, son problemas fundamentales de la geometría computacional. Ellos pueden ser resueltos en el tiempo $O(nlog n)$ para dos o tres conjuntos de puntos dimensionales, y en el tiempo coinciden con la peor complejidad de salida dada por el teorema de borde superior en dimensiones superiores.

Además de los conjuntos de puntos finitos, también se han estudiado cascos convexos para polígonos simples, movimiento browniano, curvas espaciales y epígrafes de funciones. Los cascos convexos tienen amplias aplicaciones en matemáticas, estadística, optimización combinatoria, economía, modelado geométrico y etología. Las estructuras relacionadas incluyen el casco convexo ortogonal, las capas convexas, la triangulación de Delaunay y el diagrama de Voronoi, y el cráneo convexo.

Definiciones

Hull de convexo de un conjunto de plano atado: banda de goma analogía

Un conjunto de puntos en un espacio Euclideano se define para ser convexo si contiene los segmentos de línea que conectan cada par de sus puntos. El casco convexo de un conjunto dado $X$ puede definirse como

El conjunto mínimo convexo (unique) que contiene $X$
La intersección de todos los conjuntos convexos que contienen $X$
El conjunto de todas las combinaciones convexas de puntos en $X$
La unión de todos los simplices con vértices en $X$

Para conjuntos atados en el plano Euclideano, no todos en una línea, el límite del casco convexo es la curva cerrada simple con perímetro mínimo que contiene $X$ . Uno puede imaginar estirar una banda de goma para que rodea todo el conjunto $S$ y luego la liberación, permitiendo que contraiga; cuando se hace taut, encierra el casco convexo de $S$ . Esta formulación no se generaliza inmediatamente a dimensiones superiores: para un conjunto finito de puntos en el espacio tridimensional, un barrio de un árbol de azotes de los puntos los encierra con área de superficie arbitrariamente pequeña, menor que la superficie del casco convexo. Sin embargo, en dimensiones superiores, las variantes del problema del obstáculo de encontrar una superficie mínima de energía sobre una forma determinada pueden tener el casco convexo como solución.

Para objetos en tres dimensiones, la primera definición establece que la cubierta convexa es el volumen delimitador convexo más pequeño posible de los objetos. La definición que usa intersecciones de conjuntos convexos puede extenderse a geometría no euclidiana, y la definición que usa combinaciones convexas puede extenderse de espacios euclidianos a espacios vectoriales reales arbitrarios o espacios afines; Los cascos convexos también pueden generalizarse de una manera más abstracta, a matroides orientados.

Equivalencia de definiciones

Hull 3D convex de nube de 120 puntos

No es obvio que la primera definición tenga sentido: por qué debe existir un conjunto mínimo convexo único que contenga un contenido mínimo $X$ , por cada $X$ ? Sin embargo, la segunda definición, la intersección de todos los conjuntos convexos que contienen $X$ , está bien definido. Es un subconjunto de cada otro conjunto convexo $Y$ que contiene $X$ , porque $Y$ se incluye entre los conjuntos que se intersectan. Así, es exactamente el conjunto mínimo convexo único que contiene $X$ . Por lo tanto, las dos primeras definiciones son equivalentes.

Cada conjunto convexo que contiene $X$ debe (por la suposición de que es convex) contener todas las combinaciones convexas de puntos en $X$ , por lo que el conjunto de todas las combinaciones convexas está contenido en la intersección de todos los conjuntos convexo que contienen $X$ . Por el contrario, el conjunto de todas las combinaciones convexas es en sí mismo un conjunto convexo que contiene $X$ , por lo que también contiene la intersección de todos los conjuntos convexo que contienen $X$ , y por lo tanto las definiciones segunda y tercera son equivalentes.

De hecho, según el teorema de Carathéodory, si $X$ es un subconjunto de un $d$ -dimensional Espacio euclidiano, cada combinación convexa de muchos puntos finitos de $X$ es también una combinación convexa de la mayoría $d+1$ puntos en $X$ . El conjunto de combinaciones convexas de un $(d+1)$ -tuple de puntos es un simplex; en el plano es un triángulo y en el espacio tridimensional es un tetraedro. Por lo tanto, cada combinación convexa de puntos $X$ pertenece a un simplex cuyos vértices pertenecen a $X$ , y las definiciones tercera y cuarta son equivalentes.

Cascos superior e inferior

En dos dimensiones, el casco convexo a veces se divide en dos partes, el casco superior y el casco inferior, que se extienden entre los puntos más a la izquierda y más a la derecha del casco. De manera más general, para cascos convexos en cualquier dimensión, uno puede dividir el límite del casco en puntos que miran hacia arriba (puntos para los cuales un rayo hacia arriba está separado del casco), puntos que miran hacia abajo y puntos extremos. Para cascos tridimensionales, las partes del límite que miran hacia arriba y hacia abajo forman discos topológicos.

Propiedades topológicas

Cascos cerrados y abiertos

El casco convexo cerrado de un conjunto es el cierre del casco convexo, y el casco convexo abierto es el interior (o en algunas fuentes el interior relativo) de el casco convexo.

El casco convexo cerrado $X$ es la intersección de todos los espacios cerrados que contienen $X$ . Si el casco convexo de $X$ ya es un conjunto cerrado (como sucede, por ejemplo, si $X$ es un conjunto finito o más generalmente un conjunto compacto), entonces es igual al casco convexo cerrado. Sin embargo, una intersección de medio espacio cerrado está cerrada, por lo que cuando un casco convexo no está cerrado no puede ser representado de esta manera.

Si el casco convexo abierto de un conjunto $X$ es $d$ -dimensional, entonces cada punto del casco pertenece a un casco convexo abierto de la mayoría $2d$ puntos de $X$ . Los conjuntos de vértices de un octaedro cuadrado, regular o superior-dimensional, proporcionan ejemplos donde exactamente $2d$ Se necesitan puntos.

Preservación de propiedades topológicas

La bruja de Agnesi. Los puntos sobre o sobre la curva roja proporcionan un ejemplo de un conjunto cerrado cuyo casco convexo está abierto (el medio plano superior abierto).

Topológicamente, la envolvente convexa de un conjunto abierto siempre es en sí misma abierta, y la envolvente convexa de un conjunto compacto siempre es en sí misma compacta. Sin embargo, existen conjuntos cerrados para los que el casco convexo no está cerrado. Por ejemplo, el conjunto cerrado

{displaystyle left{(x,y)mathop {bigg |} ygeq {frac {1}{1+x^{2}}}right}}

(el conjunto de puntos que se encuentran sobre o por encima de la bruja de Agnesi) tiene el semiplano superior abierto como su casco convexo.

La compacidad de las envolventes convexas de conjuntos compactos, en espacios euclidianos de dimensión finita, se generaliza mediante el teorema de Krein-Smulian, según el cual la envolvente convexa cerrada de un subconjunto débilmente compacto de un espacio de Banach (un subconjunto que es compacto bajo la topología débil) es débilmente compacto.

Puntos extremos

Un punto extremo de un conjunto convexo es un punto en el conjunto que no se encuentra en ningún segmento de línea abierto entre otros dos puntos del mismo conjunto. Para un casco convexo, cada punto extremo debe ser parte del conjunto dado, porque de lo contrario no se puede formar como una combinación convexa de puntos dados. De acuerdo con el teorema de Krein-Milman, todo conjunto compacto convexo en un espacio euclidiano (o más generalmente en un espacio vectorial topológico localmente convexo) es la envolvente convexa de sus puntos extremos. Sin embargo, esto puede no ser cierto para conjuntos convexos que no son compactos; por ejemplo, todo el plano euclidiano y la bola unitaria abierta son ambos convexos, pero ninguno tiene puntos extremos. La teoría de Choquet extiende esta teoría desde combinaciones convexas finitas de puntos extremos hasta combinaciones infinitas (integrales) en espacios más generales.

Propiedades geométricas y algebraicas

Operadora de cierre

(feminine)

El operador de casco convexo tiene las propiedades características de un operador de cierre:

Es extensiva, que significa que el casco convexo de cada conjunto $X$ es un superset de $X$ .
Es no disminución, lo que significa que, por cada dos conjuntos $X$ y $Y$ con $Xsubseteq Y$ , el casco convexo de $X$ es un subconjunto del casco convexo de $Y$ .
Es idempotente, que significa eso para cada $X$ , el casco convexo del casco convexo $X$ es el mismo que el casco convexo de $X$ .

Cuando se aplica a un conjunto finito de puntos, este es el operador de cierre de un antimatroid, el antimatroid de bombardeo del conjunto de puntos. Cada antimatroide se puede representar de esta manera mediante cascos convexos de puntos en un espacio euclidiano de dimensión suficientemente alta.

Suma de Minkowski

Las operaciones de construir la envolvente convexa y tomar la suma de Minkowski se conmutan entre sí, en el sentido de que la suma de Minkowski de envolventes convexas de conjuntos da el mismo resultado que la envolvente convexa de la suma de Minkowski de los mismos conjuntos. Esto proporciona un paso hacia el teorema de Shapley-Folkman que limita la distancia de una suma de Minkowski desde su casco convexo.

Dualidad proyectiva

La operación dual proyectiva para construir la envolvente convexa de un conjunto de puntos es construir la intersección de una familia de semiespacios cerrados que contienen el origen (o cualquier otro punto designado).

Casos especiales

Conjuntos de puntos finitos

Convex casco de puntos en el avión

El casco convexo de un punto finito ${displaystyle Ssubset mathbb {R} ^{d}}$ forma un polígono convexo cuando $d=2$ , o más generalmente un politopo convexo en $mathbb {R} ^{d}$ . Cada punto extremo del casco se llama un vértice, y (por el teorema Krein-Milman) cada polítopo convexo es el casco convexo de sus vértices. Es el polítopo convexo único cuyos vértices pertenecen a $S$ y que encierra todo $S$ . Para conjuntos de puntos en posición general, el casco convexo es un politopo simplicial.

De acuerdo con el teorema del borde superior, el número de caras del casco convexo de $n$ puntos en $d$ -dimensional El espacio de Euclide es $O(n^{lfloor d/2rfloor})$ . En particular, en dos y tres dimensiones el número de rostros es en la mayoría lineal $n$ .

Polígonos simples

Hull convexo (en azul y amarillo) de un polígono simple (en azul)

La cubierta convexa de un polígono simple encierra el polígono dado y se divide en regiones, una de las cuales es el polígono mismo. Las otras regiones, delimitadas por una cadena poligonal del polígono y un solo borde de casco convexo, se denominan bolsillos. Calcular la misma descomposición recursivamente para cada bolsillo forma una descripción jerárquica de un polígono dado llamado su árbol de diferencias convexas. Reflejar un bolsillo a través de su borde convexo del casco expande el polígono simple dado en un polígono con el mismo perímetro y un área más grande, y el teorema de Erdős-Nagy establece que este proceso de expansión eventualmente termina.

Movimiento browniano

La curva generada por el movimiento marroniano en el plano, en cualquier momento fijo, tiene probabilidad 1 de tener un casco convexo cuyo límite forma una curva continuamente diferenciable. Sin embargo, para cualquier ángulo $theta$ en el rango $<math alttext="{displaystyle pi /2<theta π π /2.Silencio Silencio .π π {displaystyle pi /2 = {theta } <img alt="{displaystyle pi /2<theta$ , habrá momentos durante el movimiento marroniano donde la partícula en movimiento toca el límite del casco convexo en un punto de ángulo $theta$ . La dimensión Hausdorff de este conjunto de tiempos excepcionales es (con alta probabilidad) ${displaystyle 1-pi /2theta }$ .

Curvas espaciales

Un oloide, el casco convexo de dos círculos en el espacio 3d

Para el casco convexo de una curva espacial o un conjunto finito de curvas espaciales en posición general en un espacio tridimensional, las partes del límite alejadas de las curvas son superficies regladas y desarrollables. Los ejemplos incluyen el oloide, el casco convexo de dos círculos en planos perpendiculares, cada uno pasando por el centro del otro, el sphericon, el casco convexo de dos semicírculos en planos perpendiculares con un centro común, y las formas D, el convexo formas obtenidas del teorema de unicidad de Alexandrov para una superficie formada al pegar dos conjuntos planos convexos de igual perímetro.

Funciones

El casco convexo o el sobre convexo inferior de una función $f$ en un espacio vectorial real es la función cuya epigrafía es el casco convexo inferior de la epígrafe de $f$ . Es la función de convex maximal única $f$ . La definición puede extenderse al casco convexo de un conjunto de funciones (obtenidos desde el casco convexo de la unión de sus epígrafes, o equivalentemente desde su mínimo punto de vista) y, en esta forma, es dual a la operación conjugada convexa.

Cálculo

En geometría computacional, se conocen varios algoritmos para calcular la envolvente convexa para un conjunto finito de puntos y para otros objetos geométricos. Calcular el casco convexo significa construir una representación inequívoca y eficiente de la forma convexa requerida. Las representaciones de salida que se han considerado para cascos convexos de conjuntos de puntos incluyen una lista de desigualdades lineales que describen las facetas del casco, un gráfico no dirigido de facetas y sus adyacencias, o la red de cara completa del casco. En dos dimensiones, puede ser suficiente enumerar los puntos que son vértices, en su orden cíclico alrededor del casco.

Para los cascos convexos en dos o tres dimensiones, la complejidad de los algoritmos correspondientes se calcula generalmente en términos de $n$ , el número de puntos de entrada, y $h$ , el número de puntos en el casco convexo, que puede ser significativamente menor que $n$ . Para los cascos de mayor dimensión, el número de caras de otras dimensiones también puede entrar en el análisis. Graham scan puede calcular el casco convexo de $n$ puntos en el avión a tiempo $O(nlog n)$ . Para puntos en dos y tres dimensiones, se conocen algoritmos más complicados sensibles a la salida que calculan el casco convexo en el tiempo $O(nlog h)$ . Estos incluyen el algoritmo de Chan y el algoritmo Kirkpatrick-Seidel. Para dimensiones $3}" xmlns="http://www.w3.org/1998/Math/MathML">d■3{displaystyle d espíritu3}3}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/58db34887c6f7dafa930e0a4f17834a8e14469df" style="vertical-align: -0.338ex; width:5.477ex; height:2.176ex;"/>$ , el tiempo para computar el casco convexo es $O(n^{lfloor d/2rfloor})$ , coincidiendo con la peor complejidad de salida del problema. El casco convexo de un simple polígono en el plano se puede construir en tiempo lineal.

Las estructuras de datos de casco convexo dinámico se pueden usar para realizar un seguimiento del casco convexo de un conjunto de puntos que experimentan inserciones y eliminaciones de puntos, y las estructuras de casco convexo cinético pueden realizar un seguimiento del casco convexo para puntos que se mueven continuamente. La construcción de cascos convexos también sirve como herramienta, un bloque de construcción para una serie de otros algoritmos geométricos computacionales, como el método de calibradores giratorios para calcular el ancho y el diámetro de un conjunto de puntos.

Estructuras relacionadas

Ortogonal convex hull

Muñeca convexa relativa

Se pueden definir varias otras formas a partir de un conjunto de puntos de forma similar al casco convexo, como el superconjunto mínimo con alguna propiedad, la intersección de todas las formas que contienen los puntos de una familia de formas dada, o la unión de todas las combinaciones de puntos para un determinado tipo de combinación. Por ejemplo:

El casco affine es el subespacio affine más pequeño de un espacio euclidiano que contiene un conjunto dado, o la unión de todas las combinaciones de puntos affine en el conjunto.
El casco lineal es el subespacio lineal más pequeño de un espacio vectorial que contiene un conjunto dado, o la unión de todas las combinaciones lineales de puntos en el conjunto.
El casco cónico o el casco positivo de un subconjunto de un espacio vectorial es el conjunto de todas las combinaciones positivas de puntos en el subconjunto.
El casco visual de un objeto tridimensional, con respecto a un conjunto de puntos de vista, consta de los puntos $p$ tal que cada rayo desde un punto de vista $p$ interseca el objeto. Equivalentemente es la intersección de los conos (no-convexo) generados por el contorno del objeto con respecto a cada punto de vista. Se utiliza en la reconstrucción 3D como la forma más grande que podría tener los mismos esquemas desde los puntos de vista dados.
El casco circular o alfa-hull de un subconjunto del plano es la intersección de todos los discos con un radio dado ${displaystyle 1/alpha }$ que contienen el subconjunto.
El casco convexo relativo de un subconjunto de un polígono simple bidimensional es la intersección de todos los supersets relativamente convexos, donde un conjunto dentro del mismo polígono es relativamente convexo si contiene la geodésica entre cualquiera de sus dos puntos.
El casco convexo ortogonal o el casco convexo rectilineal es la intersección de todos los supersets convexos ortogonales y conectados, donde un conjunto es convexo ortogonal si contiene todos los segmentos axis-paralelos entre pares de sus puntos.
El casco convexo ortogonal es un caso especial de una construcción mucho más general, el casco hiperconvex, que se puede considerar como el espacio métrico más pequeño que contiene los puntos de un espacio métrico dado.
El casco convexo holomorfo es una generalización de conceptos similares a complejos manifolds analíticos, obtenidos como una intersección de conjuntos subnivel de funciones holomorfas que contienen un conjunto dado.

La triangulación Delaunay de un conjunto de puntos y su doble, el diagrama Voronoi, están matemáticamente relacionados con los cascos convexos: la triangulación Delaunay de un punto establecido en $mathbb {R} ^{n}$ se puede ver como la proyección de un casco convexo en ${displaystyle mathbb {R} ^{n+1}.}$ Las formas alfa de un conjunto de puntos finitos dan a una familia anidada de objetos geométricos (no-convexo) que describen la forma de un punto fijado en diferentes niveles de detalle. Cada forma de alfa es la unión de algunas de las características de la triangulación Delaunay, seleccionada comparando su circunradius con el parámetro alpha. El punto se estableció forma un punto final de esta familia de formas, y su casco convexo forma el otro punto final. Las capas convexas de un conjunto de puntos son una familia anidada de polígonos convexos, la más externa de los cuales es el casco convexo, con las capas interiores construidas recursivamente desde los puntos que no son vértices del casco convexo.

El cráneo convexo de un polígono es el polígono convexo más grande contenido en su interior. Se puede encontrar en tiempo polinomial, pero el exponente del algoritmo es alto.

Aplicaciones

Los cascos convexos tienen amplias aplicaciones en muchos campos. Dentro de las matemáticas, los cascos convexos se utilizan para estudiar polinomios, valores propios de matrices y elementos unitarios, y varios teoremas en geometría discreta involucran cascos convexos. Se utilizan en estadísticas robustas como el contorno más externo de la profundidad de Tukey, son parte de la visualización de datos bidimensionales en diagramas de bolsa y definen conjuntos de riesgo de reglas de decisión aleatorias. Los cascos convexos de vectores indicadores de soluciones a problemas combinatorios son fundamentales para la optimización combinatoria y la combinatoria poliédrica. En economía, los cascos convexos se pueden utilizar para aplicar métodos de convexidad en economía a mercados no convexos. En el modelado geométrico, la propiedad del casco convexo de las curvas de Bézier ayuda a encontrar sus cruces, y los cascos convexos son parte de la medición de los cascos de los barcos. Y en el estudio del comportamiento animal, los cascos convexos se utilizan en una definición estándar del área de distribución.

Matemáticas

Partition of seven points into three subsets with intersecting convex hulls, guaranteed to exist for any seven points in the plano by Tverberg's theorem

Los polígonos de Newton de polinomios univariados y los politopos de Newton de polinomios multivariados son cascos convexos de puntos derivados de los exponentes de los términos del polinomio y se pueden utilizar para analizar el comportamiento asintótico del polinomio y las valoraciones de sus raíces. Los cascos convexos y los polinomios también se unen en el teorema de Gauss-Lucas, según el cual las raíces de la derivada de un polinomio se encuentran todas dentro del casco convexo de las raíces del polinomio.

En el análisis espectral, el rango numérico de una matriz normal es la envolvente convexa de sus valores propios. El teorema de Russo-Dye describe las envolventes convexas de elementos unitarios en un C*-álgebra. En geometría discreta, tanto el teorema de Radon como el de Tverberg se refieren a la existencia de particiones de conjuntos de puntos en subconjuntos con cascos convexos que se cruzan.

Las definiciones de un conjunto convexo que contiene segmentos de línea entre sus puntos, y de un casco convexo como la intersección de todos los superconjuntos convexos, se aplican tanto a los espacios hiperbólicos como a los espacios euclidianos. Sin embargo, en el espacio hiperbólico, también es posible considerar las envolventes convexas de conjuntos de puntos ideales, puntos que no pertenecen al espacio hiperbólico en sí, sino que se encuentran en el límite de un modelo de ese espacio. Los límites de los cascos convexos de los puntos ideales del espacio hiperbólico tridimensional son análogos a las superficies regladas en el espacio euclidiano, y sus propiedades métricas juegan un papel importante en la conjetura de geometrización en la topología de baja dimensión. Los cascos convexos hiperbólicos también se han utilizado como parte del cálculo de triangulaciones canónicas de variedades hiperbólicas y se han aplicado para determinar la equivalencia de nudos.

Vea también la sección sobre movimiento browniano para la aplicación de cascos convexos a este tema, y la sección sobre curvas espaciales para su aplicación a la teoría de superficies desarrollables.

Estadísticas

Un bagplot. La región a la sombra exterior es el casco convexo, y la región a la sombra interior es el contorno de profundidad del 50% Tukey.

En estadísticas robustas, el casco convexo proporciona uno de los componentes clave de un diagrama de bolsa, un método para visualizar la dispersión de puntos de muestra bidimensionales. Los contornos de la profundidad de Tukey forman una familia anidada de conjuntos convexos, con el casco convexo en la parte exterior, y la gráfica de bolsa también muestra otro polígono de esta familia anidada, el contorno de 50% de profundidad.

En la teoría de la decisión estadística, el conjunto de riesgo de una regla de decisión aleatoria es la envolvente convexa de los puntos de riesgo de sus reglas de decisión deterministas subyacentes.

Optimización combinatoria

En optimización combinatoria y combinatoria poliédrica, los objetos centrales de estudio son los cascos convexos de vectores indicadores de soluciones a un problema combinatorio. Si se pueden encontrar las facetas de estos politopos, describiendo los politopos como intersecciones de medios espacios, entonces se pueden usar algoritmos basados en programación lineal para encontrar soluciones óptimas. En la optimización multiobjetivo, también se utiliza un tipo diferente de casco convexo, el casco convexo de los vectores de peso de las soluciones. Uno puede maximizar cualquier combinación cuasiconvexa de pesos al encontrar y verificar cada vértice del casco convexo, a menudo de manera más eficiente que verificar todas las soluciones posibles.

Economía

En el modelo Arrow-Debreu de equilibrio económico general, se supone que los agentes tienen conjuntos presupuestarios convexos y preferencias convexas. Estos supuestos de convexidad en economía pueden usarse para probar la existencia de un equilibrio. Cuando los datos económicos reales no son convexos, se pueden hacer convexos tomando cascos convexos. El teorema de Shapley-Folkman se puede utilizar para demostrar que, para mercados grandes, esta aproximación es precisa y conduce a un "cuasi-equilibrio" para el mercado no convexo original.

Modelado geométrico

En el modelado geométrico, una de las propiedades clave de una curva de Bézier es que se encuentra dentro del casco convexo de sus puntos de control. Esta llamada "propiedad del casco convexo" se puede utilizar, por ejemplo, para detectar rápidamente las intersecciones de estas curvas.

En la geometría del diseño de embarcaciones y barcos, la circunferencia de la cadena es una medida del tamaño de una embarcación de vela, definida mediante el casco convexo de una sección transversal del casco de la embarcación. Se diferencia de la circunferencia de la piel, el perímetro de la sección transversal en sí, a excepción de los barcos y barcos que tienen un casco convexo.

Etología

El casco convexo se conoce comúnmente como el polígono convexo mínimo en etología, el estudio del comportamiento animal, donde es un enfoque clásico, aunque quizás simplista, para estimar el área de distribución de un animal en función de los puntos donde el animal ha sido observado. Los valores atípicos pueden hacer que el polígono convexo mínimo sea demasiado grande, lo que ha motivado enfoques relajados que contienen solo un subconjunto de las observaciones, por ejemplo, eligiendo una de las capas convexas que está cerca de un porcentaje objetivo de las muestras, o en el casco convexo local método mediante la combinación de cascos convexos de vecindades de puntos.

Física cuántica

En la física cuántica, el espacio de estado de cualquier sistema cuántico, el conjunto de todas las formas en que se puede preparar el sistema, es una envolvente convexa cuyos puntos extremos son operadores semidefinidos positivos conocidos como estados puros y cuyos puntos interiores se denominan estados mixtos.. El teorema de Schrödinger-HJW demuestra que, de hecho, cualquier estado mixto puede escribirse como una combinación convexa de estados puros de múltiples formas.

Termodinámica

Hull convexo de compuestos de magnesio-carbono. Mg₂C₃ se espera que sea inestable ya que está por encima del casco inferior.

Josiah Willard Gibbs (1873) identificó un casco convexo en termodinámica, aunque el artículo se publicó antes de que se llamara así al casco convexo. En un conjunto de energías de varias estequiometrías de un material, solo serán estables aquellas medidas en el casco convexo inferior. Al eliminar un punto del casco y luego calcular su distancia al casco, su distancia al nuevo casco representa el grado de estabilidad de la fase.

Historia

El casco inferior convexo de puntos en el plano aparece, en forma de polígono de Newton, en una carta de Isaac Newton a Henry Oldenburg en 1676. El término "casco convexo" aparece ya en la obra de Garrett Birkhoff (1935), y el término correspondiente en alemán aparece antes, por ejemplo, en la reseña de Hans Rademacher de Kőnig (1922). Otros términos, como "sobre convexo", también se utilizaron en este período de tiempo. En 1938, según Lloyd Dines, el término "casco convexo" se había convertido en estándar; Dines agrega que encuentra el término desafortunado, porque el significado coloquial de la palabra "casco" sugeriría que se refiere a la superficie de una forma, mientras que el casco convexo incluye el interior y no solo la superficie.

Te puede interesar
David hilbert
(leer más)
Te puede interesar
Sistema L
(leer más)
Te puede interesar
Producto directo
(leer más)
Más resultados...