Capacidad calorífica molar
La capacidad calorífica molar de una sustancia química es la cantidad de energía que se debe añadir, en forma de calor, a un mol de la sustancia para provocar un aumento de una unidad en su temperatura. Alternativamente, es la capacidad calorífica de una muestra de la sustancia dividida por la cantidad de sustancia de la muestra; o también la capacidad calorífica específica de la sustancia multiplicada por su masa molar. La unidad SI de capacidad calorífica molar es julio por kelvin por mol, J⋅K−1⋅mol−1.
Como el calor específico, la capacidad de calor molar medida de una sustancia, especialmente un gas, puede ser significativamente mayor cuando se permite que la muestra se expanda ya que se calienta (a presión constanteo isobaric) que cuando se calienta en un recipiente cerrado que evita la expansión (a volumen constanteo isocoric). La relación entre ambos, sin embargo, es la misma relación de capacidad de calor obtenida de las capacidades de calor específicas correspondientes.
Esta propiedad es más relevante en química, cuando las cantidades de sustancias a menudo se especifican en moles en lugar de en masa o volumen. La capacidad calorífica molar generalmente aumenta con la masa molar, a menudo varía con la temperatura y la presión y es diferente para cada estado de la materia. Por ejemplo, a presión atmosférica, la capacidad calorífica molar (isobárica) del agua justo por encima del punto de fusión es aproximadamente 76 J⋅K−1⋅mol−1, pero eso de hielo justo debajo de ese punto es aproximadamente 37,84 J⋅K−1⋅mol−1. Mientras la sustancia experimenta una transición de fase, como fusión o ebullición, su capacidad calorífica molar es técnicamente infinita, porque el calor cambia su estado en lugar de aumentar su temperatura. El concepto no es apropiado para sustancias cuya composición precisa se desconoce o cuya masa molar no está bien definida, como polímeros y oligómeros de tamaño molecular indeterminado.
Una propiedad estrechamente relacionada de una sustancia es la capacidad calorífica por mol de átomos, o capacidad calorífica átomo-molar, en la que se divide la capacidad calorífica de la muestra. por el número de moles de átomos en lugar de moles de moléculas. Entonces, por ejemplo, la capacidad calorífica atómica-molar del agua es 1/3 de su capacidad calorífica molar, es decir, 25,3 J⋅K−1⋅mol−1.
En contextos de química informal, la capacidad calorífica molar puede denominarse simplemente "capacidad calorífica" o "calor específico". Sin embargo, las normas internacionales ahora recomiendan que la "capacidad calorífica específica" Siempre haga referencia a capacidad por unidad de masa, para evitar posibles confusiones. Por lo tanto, para esta cantidad siempre se debe utilizar la palabra "molar", no "específica".
Definición
La capacidad calorífica molar de una sustancia, que puede denotarse por cm, es la capacidad calorífica C de una muestra de la sustancia, dividida por la cantidad (moles) n de la sustancia en la muestra:
- cm
donde Q es la cantidad de calor necesaria para elevar la temperatura de la muestra en ΔT. Obviamente, este parámetro no se puede calcular cuando n no se conoce o no se define.
Al igual que la capacidad calorífica de un objeto, la capacidad calorífica molar de una sustancia puede variar, a veces sustancialmente, dependiendo de la temperatura inicial T de la muestra y la presión P aplicado a él. Por lo tanto, debe considerarse una función cm(P,T) de esas dos variables.
Estos parámetros generalmente se especifican al dar la capacidad calorífica molar de una sustancia. Por ejemplo, "H2O: 75,338 J⋅K−1⋅mol−1 (25 °C, 101,325 kPa) " Cuando no se especifican, los valores publicados de la capacidad calorífica molar cm generalmente son válidos para algunas condiciones estándar de temperatura y presión.
Sin embargo, la dependencia de cm(P,T) de la temperatura y presión iniciales a menudo puede ser ignorado en contextos prácticos, p.e. cuando se trabaja en rangos estrechos de esas variables. En esos contextos, normalmente se puede omitir el calificador (P,T) y aproximar la capacidad calorífica molar mediante una constante cm. adecuado para esos rangos.
Dado que la capacidad calorífica molar de una sustancia es el calor específico c multiplicado por la masa molar de la sustancia M/N su valor numérico es generalmente menor que el del calor específico. La cera de parafina, por ejemplo, tiene un calor específico de aproximadamente 2500 J⋅K−1 ⋅kg−1 pero una capacidad calorífica molar de aproximadamente 600 J⋅ K−1⋅mol−1.
La capacidad calorífica molar es una prueba "intensiva" Propiedad de una sustancia, característica intrínseca que no depende del tamaño o forma de la cantidad considerada. (El calificativo "específico" delante de una propiedad extensiva a menudo indica una propiedad intensiva derivada de ella).
Variaciones
La inyección de energía térmica en una sustancia, además de elevar su temperatura, suele provocar un aumento de su volumen o de su presión, dependiendo de cómo esté confinada la muestra. La elección de este último influye en la capacidad calorífica molar medida, incluso para la misma presión inicial P y temperatura inicial T. Se utilizan ampliamente dos opciones particulares:
- Si la presión se mantiene constante (por ejemplo, a la presión atmosférica ambiental), y se permite ampliar la muestra, la expansión genera trabajo a medida que la fuerza de la presión desplaza el recinto. Ese trabajo debe provenir de la energía térmica proporcionada. Se dice que el valor obtenido es la capacidad de calor molar a presión constante (o isobaric), y es a menudo denotado cP,m, cp,m, cP,m, etc.
- Por otra parte, si se evita la expansión, por ejemplo por un recinto suficientemente rígido, o aumentando la presión externa para contrarrestar el interior, no se genera trabajo, y la energía térmica que hubiera entrado en él debe contribuir en cambio a la energía interna del objeto, incluyendo elevar su temperatura por una cantidad adicional. El valor obtenido de esta manera se dice que es la capacidad de calor molar a volumen constante (o isocoric) y denotado cV,m, cv,m, cv,m, etc.
El valor de cV,m es siempre menos que el valor cP,m. Esta diferencia es particularmente notable en los gases donde los valores bajo presión constante son generalmente 30% a 66,7% mayor que los que tienen volumen constante.
Todos los métodos para la medición del calor específico se aplican también a la capacidad de calor molar.
Unidades
La unidad SI de capacidad calorífica molar es julio por kelvin por mol (J/(K⋅mol), J/(K mol), J K−1 mol−1< /sup>, etc.). Dado que un incremento de temperatura de un grado Celsius es lo mismo que un incremento de un kelvin, es lo mismo que un julio por grado Celsius por mol (J/(°C⋅mol)).
En química, las cantidades de calor todavía se miden a menudo en calorías. De manera confusa, dos unidades con ese nombre, denominadas "cal" o "Cal", se han utilizado comúnmente para medir cantidades de calor:
- la "pequeña calorías" (o "gram-calorie", "cal") es 4.184 J, exactamente.
- La "grand calorías" (también "kilocalorie", "kilogram-calorie", o "calor de alimentos"; "kcal" o "Cal") es 1000 calorías pequeñas, es decir, 4184 J, exactamente.
Cuando el calor se mide en estas unidades, la unidad de calor específico es generalmente
- 1 cal/(°C⋅mol) ("pequeña calorías") = 4.184 J⋅K−1⋅mol−1
- 1 kcal/(°C⋅mol) ("gran calorías") = 4184 J⋅K−1⋅mol−1.
La capacidad calorífica molar de una sustancia tiene la misma dimensión que la capacidad calorífica de un objeto; es decir, L2⋅M⋅T−2⋅Θ−1, o M(L/T)2/Θ. (De hecho, es la capacidad calorífica del objeto la que consta de un número de Avogadro de moléculas de la sustancia). Por lo tanto, la unidad SI J⋅K−1⋅mol−1 equivale a kilogramo metro cuadrado por segundo cuadrado por kelvin (kg⋅m2⋅K−1⋅s−2).
Base física
Gases monoatómicos
La temperatura de una muestra de una sustancia refleja la energía cinética promedio de sus partículas constituyentes (atoms o moléculas) en relación con su centro de masa. La mecánica cuántica predice que, a temperatura ambiente y presiones ordinarias, un átomo aislado en un gas no puede almacenar ninguna cantidad significativa de energía excepto en forma de energía cinética. Por lo tanto, cuando un número determinado N de los átomos de un gas monatómico recibe una entrada Q de energía térmica, en un contenedor de volumen fijo, la energía cinética de cada átomo aumentará Q/NIndependientemente de la masa del átomo. Esta suposición es la base de la teoría de los gases ideales.
En otras palabras, esa teoría predice que la capacidad calorífica molar a volumen constante cV,m de todos los gases monoatómicos será el mismo; específicamente,
- cV,m = 3/2R
Donde R es la constante de gas ideal, alrededor de 8.31446 J⋅K−1⋅mol−1 (que es el producto de la constante Boltzmann kB y la constante de Avogadro). Y, de hecho, los valores experimentales cV,m para los gases nobles helio, neón, argón, krypton y xenón (a 1 atm y 25 °C) son todos 12.5 J⋅K−1⋅mol−1, que es 3/2R; aunque sus pesos atómicos oscilan entre 4 y 131.
La misma teoría predice que la capacidad calorífica molar de un gas monoatómico a presión constante será
- cP,m = cV,m + R = 5/2R
Esta predicción coincide con los valores experimentales, que, para el helio hasta el xenón, son 20,78, 20,79, 20,85, 20,95 y 21,01 J⋅K−1⋅mol−1, respectivamente; muy cerca del teórico 5/< span class="den">2R = 20,78 J⋅K−1⋅mol−1< /sup>.
Por lo tanto, el calor específico (por unidad de masa, no por mol) de un gas monoatómico será inversamente proporcional a su masa atómica relativa (adimensional) A. Es decir, aproximadamente,
- cV = (12470 J⋅K−1⋅kg−1)/A cP = (20786 J⋅K−1⋅kg−1)/A
Gases poliatómicos

Grados de libertad
Una molécula poliatómica (que consta de dos o más átomos unidos) puede almacenar energía térmica en otras formas además de su energía cinética. Estas formas incluyen la rotación de la molécula y la vibración de los átomos en relación con su centro de masa.
Estos grados de libertad adicionales contribuyen a la capacidad calorífica molar de la sustancia. Es decir, cuando se inyecta energía térmica en un gas con moléculas poliatómicas, sólo una parte se destinará a aumentar su energía cinética y, por tanto, la temperatura; el resto irá a esos otros grados de libertad. Así, para lograr el mismo aumento de temperatura, será necesario proporcionar más energía térmica a un mol de esa sustancia que a un mol de un gas monoatómico. Por lo tanto, las sustancias con un alto número de átomos por molécula, como el octano, pueden tener una capacidad calorífica muy grande por mol y, sin embargo, un calor específico relativamente pequeño (por unidad de masa).
Si la molécula pudiera describirse completamente usando la mecánica clásica, entonces el teorema de equipartición de energía podría usarse para predecir que cada grado de libertad tendría una energía promedio en la cantidad de 1/2kT, donde k es la constante de Boltzmann y T es la temperatura. Si el número de grados de libertad de la molécula es f, entonces cada molécula tendría, en promedio, una energía total igual a 1/2 fkT. Entonces la capacidad calorífica molar (a volumen constante) sería
- cV,m = 1/2f
donde R es la constante de los gases ideales. Según la relación de Mayer, la capacidad calorífica molar a presión constante sería
- cP,m = cV,m + R = 1/2f + R = 1/2(f + 2)R
Así, cada grado de libertad adicional contribuirá 1/2R a la capacidad calorífica molar del gas (ambos cV,m y cP,m).
En particular, cada molécula de un gas monoatómico tiene sólo f = 3 grados de libertad, es decir, los componentes de su vector de velocidad; por lo tanto cV,m = 3/2R y cP,m = 5/2R .
Modos de rotación de una molécula diatómica
Por ejemplo, la capacidad calorífica molar del nitrógeno N
2 a volumen constante es 20,6 J⋅K− 1⋅mol−1 (a 15 °C, 1 atm), que es 2,49 R. De la ecuación teórica cV,m = 1/2fR, se concluye que cada molécula tiene f = 5 grados de libertad. Estos resultan ser tres grados del vector velocidad de la molécula, más dos grados de su rotación alrededor de un eje que pasa por el centro de masa y es perpendicular a la línea de los dos átomos. Los grados de libertad debidos a traslaciones y rotaciones se denominan grados de libertad rígidos, ya que no implican ninguna deformación de la molécula.
Debido a esos dos grados de libertad adicionales, la capacidad calorífica molar cV,m de N< sup style="font-size:inherit;line-height:inherit;vertical-align:baseline">
2 (20,6 J⋅K−1⋅mol−1) es mayor que el de un gas monoatómico hipotético (12,5 J⋅K−1⋅mol−1) por un factor de < span class="num">5/3.
Grados de libertad congelados y activos
Según la mecánica clásica, una molécula diatómica como el nitrógeno debería tener más grados de libertad interna, correspondientes a la vibración de los dos átomos que estiran y comprimen el enlace entre ellos.
Para propósitos termodinámicos, cada dirección en la que un átomo puede vibrar independientemente en relación con el resto de la molécula introduce dos grados de libertad: uno asociado con la energía potencial proveniente de la distorsión de los enlaces y otro para la energía cinética del átomo. La moción de 39; En una molécula diatómica como N
2, solo hay una dirección para la vibración y los movimientos de los dos átomos deben ser opuestos pero iguales; entonces sólo hay dos grados de libertad vibratoria. Eso llevaría f a 7 y cV,m a 3,5 R.
La razón por la que estas vibraciones no absorben la fracción esperada de energía térmica aportada es la mecánica cuántica. Según esa teoría, la energía almacenada en cada grado de libertad debe aumentar o disminuir sólo en determinadas cantidades (cuantos). Por lo tanto, si la temperatura T del sistema no es lo suficientemente alta, la energía promedio que estaría disponible para algunos de los grados de libertad teóricos (kT/f ) puede ser inferior al cuanto mínimo correspondiente. Si la temperatura es lo suficientemente baja, ese puede ser el caso de prácticamente todas las moléculas. Entonces se dice que esos grados de libertad están "congelados". La capacidad calorífica molar del gas estará entonces determinada únicamente por la energía "activa". grados de libertad que, para la mayoría de las moléculas, pueden recibir suficiente energía para superar ese umbral cuántico.

Para cada grado de libertad, existe una temperatura crítica aproximada a la que se "se descongela" ("descongela") y se vuelve activo, pudiendo así retener energía térmica. Para los tres grados de libertad de traslación de las moléculas de un gas, esta temperatura crítica es extremadamente pequeña, por lo que se puede suponer que están siempre activas. Para los grados de libertad de rotación, la temperatura de descongelación suele ser de unas pocas decenas de kelvin (aunque con una molécula muy ligera como el hidrógeno, los niveles de energía de rotación estarán tan espaciados que la capacidad calorífica de rotación puede no "descongelarse" por completo). ; hasta que se alcancen temperaturas considerablemente más altas). Los modos de vibración de las moléculas diatómicas generalmente comienzan a activarse sólo muy por encima de la temperatura ambiente.
En el caso del nitrógeno, los grados de libertad de rotación ya están completamente activos a -173 °C (100 K, sólo 23 K por encima del punto de ebullición). Por otro lado, los modos de vibración sólo empiezan a activarse alrededor de 350 K (77 °C). Por lo tanto, la capacidad calorífica molar cP,m es casi constante en 29,1 J⋅K−1⋅mol−1 desde 100 K hasta aproximadamente 300 °C. Aproximadamente a esa temperatura, comienza a aumentar rápidamente y luego vuelve a disminuir. Es 35,5 J⋅K−1⋅mol−1 a 1500 °C, 36,9 a 2500 °C y 37,5 a 3500 °C. El último valor corresponde casi exactamente al valor previsto para f = 7.

La siguiente es una tabla de algunas capacidades caloríficas molares a presión constante cP,m de varios gases diatómicos a temperatura estándar (25 °C = 298 K), a 500 °C y a 5000 °C, y el número aparente de grados de libertad f* estimado mediante la fórmula f * = 2cP,m/R − 2 :
| 25 °C | 500 °C | 5000 °C | |||||
|---|---|---|---|---|---|---|---|
| Gas | cP,m J⋅K−1⋅mol−1 | f* | cP,m J⋅K−1⋅mol−1 | f* | cP,m J⋅K−1⋅mol−1 | f* | |
| H2 | 28.9 | 5.0 | 29.6 | 5.1 | 41.2 | 7.9 | No saturado. |
| CO | 29.1 | 5.0 | 31,7 | 5.6 | 38.1 | 7.2 | Saturado. |
| N2 | 29.1 | 5.0 | 31.3 | 5,5 | 38.0 | 7.1 | Saturado. |
| Cl2 | 34.0 | 6.2 | 37.0 | 6.9 | 39.6 | 7.5 | Max 41.3 a ~3700 C. |
| Br2 (vapour) | (*)36.4 | 6.8 | 37,5 | 7.0 | 39.2 | 7.4 | Max 41.6 en ~3000 C. |
(*) A 59 C (punto de ebullición)
La aproximación del oscilador armónico cuántico implica que el espaciado de los niveles de energía de los modos vibratorios es inversamente proporcional a la raíz cuadrada de la masa reducida de los átomos que componen la molécula diatómica. Este hecho explica por qué los modos vibratorios de moléculas más pesadas como Br
2 están activos a temperaturas más bajas. La capacidad calorífica molar de Br
2 a temperatura ambiente es consistente con f = 7 grados de libertad , el máximo para una molécula diatómica. A temperaturas suficientemente altas, todos los gases diatómicos se aproximan a este valor.
Modos rotacionales de átomos individuales
La mecánica cuántica también explica por qué el calor específico de los gases monoatómicos es bien predicho por la teoría de los gases ideales con el supuesto de que cada molécula es una masa puntual que tiene solo f = 3 grados de libertad de traslación. .
Según la mecánica clásica, dado que los átomos tienen un tamaño distinto de cero, también deberían tener tres grados de libertad de rotación, o f = 6 en total. Asimismo, la molécula de nitrógeno diatómico debería tener un modo de rotación adicional, es decir, alrededor de la línea de los dos átomos; y por lo tanto tenemos f = 6 también. En la visión clásica, cada uno de estos modos debería almacenar una parte igual de la energía térmica.
Sin embargo, según la mecánica cuántica, la diferencia de energía entre los estados de rotación permitidos (cuantizados) es inversamente proporcional al momento de inercia alrededor del eje de rotación correspondiente. Debido a que el momento de inercia de un solo átomo es extremadamente pequeño, la temperatura de activación de sus modos de rotación es extremadamente alta. Lo mismo se aplica al momento de inercia de una molécula diatómica (o poliatómica lineal) alrededor del eje internuclear, razón por la cual ese modo de rotación no está activo en general.
Por otro lado, los electrones y los núcleos pueden existir en estados excitados y, en algunos casos excepcionales, pueden estar activos incluso a temperatura ambiente, o incluso a temperaturas criogénicas.
Gases poliatómicos
El conjunto de todas las formas posibles de desplazar infinitamente los átomos n de una molécula de gas poliatómico es un espacio lineal de dimensión 3n, porque cada átomo puede desplazarse independientemente en cada una de las tres direcciones del eje ortogonal. Sin embargo, algunas de estas dimensiones son simplemente traslación de la molécula mediante un vector de desplazamiento infinitesimal, y otras son simplemente rotaciones rígidas de la misma en un ángulo infinitesimal alrededor de algún eje. Otros más pueden corresponder a la rotación relativa de dos partes de la molécula alrededor de un enlace simple que las conecta.
Los modos de deformación independientes (formas linealmente independientes de deformar realmente la molécula, que tensan sus enlaces) son sólo las dimensiones restantes de este espacio. Como en el caso de las moléculas diatómicas, cada uno de estos modos de deformación cuenta como dos grados de libertad vibratorios a efectos de almacenamiento de energía: uno para la energía potencial almacenada en los enlaces tensos y otro para la energía cinética extra de los átomos cuando vibran alrededor del cuerpo. Configuración en reposo de la molécula.
En particular, si la molécula es lineal (con todos los átomos en línea recta), solo tiene dos modos de rotación no triviales, ya que la rotación alrededor de su propio eje no desplaza ningún átomo. Por lo tanto, tiene 3n − 5 modos de deformación reales. El número de grados de libertad que almacenan energía es entonces f = 3 + 2 + 2(3n − 5) = 6n − 5 .
Por ejemplo, la molécula lineal de óxido nitroso N≡N=O (con n = 3) tiene 3n − 5 = 4 modos de deformación infinitesimales independientes. Dos de ellos pueden describirse como estirando uno de los enlaces mientras el otro conserva su longitud normal. Los otros dos se pueden identificar que la molécula se dobla en el átomo central, en las dos direcciones que son ortogonales a su eje. En cada modo, se debe suponer que los átomos se desplazan de modo que el centro de masa permanece estacionario y no hay rotación. La molécula entonces tiene f = 6n − 5 = 13 grados de libertad totales de almacenamiento de energía (3 traslacionales, 2 rotacionales, 8 vibratorios). A una temperatura suficientemente alta, su capacidad calorífica molar debería ser cP,m = 7,5 R = 62,63 J ⋅K−1⋅mol−1. Para cianógeno N≡C−C≡N y acetileno H−C≡C−H (n = 4) el mismo análisis arroja f = 19 y predice cP,m = 10,5 < i>R = 87,3 J⋅K−1⋅mol−1.
Una molécula con n átomos que es rígida y no lineal tiene 3 modos de traslación y 3 modos de rotación no triviales, por lo tanto, solo 3n − 6 modos de deformación. Por lo tanto, tiene f = 3 + 3 + 2(3n − 6) = 6n − 6 grados de libertad de absorción de energía (un menos que una molécula lineal con el mismo número de átomos). El agua H2O (n = 3) está doblada en su forma no -estado tenso, por lo tanto se predice que tendrá f = 12 grados de libertad. El metano CH4 (n = 5) es tridimensional y la fórmula predice f = 24.
Etano H3C−CH3 (n = 8) tiene 4 grados de libertad de rotación: dos alrededor de ejes que son perpendiculares al enlace central, y dos más porque cada grupo metilo puede girar independientemente alrededor de ese enlace, con resistencia insignificante. Por lo tanto, el número de modos de deformación independientes es 3n − 7, lo que da f = 3 + 4 + 2(3n − 7) = 6norte − 7 = 41.
La siguiente tabla muestra las capacidades caloríficas molares experimentales a presión constante cP,m de los gases poliatómicos anteriores a temperatura estándar (25 °C = 298 K), a 500 °C y a 5000 °C, y el número aparente de grados de libertad f* estimado mediante la fórmula f * = 2cP,m/R − 2 :
| 25 °C | 500 °C | 5000 °C | ||||||
|---|---|---|---|---|---|---|---|---|
| Gas | cP,m J⋅K−1⋅mol−1 | f* | cP,m J⋅K−1⋅mol−1 | f* | cP,m J⋅K−1⋅mol−1 | f* | f | Notas |
| NanceN=O | 38.6 | 7.3 | 51.8 | 10,5 | 62.0 | 12.9 | 13 | |
| NADOC–CADON | 56,7 | 11.6 | 72.3 | 15.4 | 86.7 | 18.9 | 19 | |
| H-CngelC-N | 44.0 | 8.6 | 63.2 | 13.2 | 92,9 | 20.3 | 19 | |
| H2O | — | — | 38.4 | 7.2 | 59,7 | 12.4 | 12 | |
| CH4 | 35,7 | 6.6 | 61.6 | 12.8 | 105.7 | 23.4 | 24 | |
| H3C-CH3 | 52,5 | 10.6 | 105.6 | 23.4 | 168,7 | (*)38.6 | 41 | |
(*) A 3000C
Calor específico de los sólidos
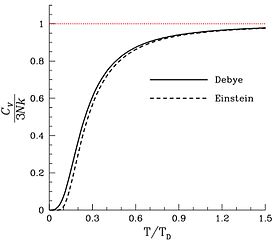
En la mayoría de los sólidos (pero no en todos), las moléculas tienen una posición y orientación media fija y, por lo tanto, los únicos grados de libertad disponibles son las vibraciones de los átomos. Por tanto, el calor específico es proporcional al número de átomos (no moléculas) por unidad de masa, que es la ley de Dulong-Petit. Otras contribuciones pueden provenir de los grados de libertad magnéticos en los sólidos, pero rara vez hacen contribuciones sustanciales. y electronico Dado que cada átomo del sólido aporta un modo de vibración independiente, el número de grados de libertad en n átomos es 6n. Por lo tanto, se espera que la capacidad calorífica de una muestra de una sustancia sólida sea 3RNa, o (24,94 J/K)N< sub>a, donde Na es el número de moles de átomos en la muestra, no moléculas. Dicho de otra manera, se espera que la capacidad calorífica átomo-molar de una sustancia sólida sea 3R = 24,94 J⋅K−1⋅mol −1, donde "amol" denota una cantidad del sólido que contiene el número de átomos de Avogadro.
De ello se deduce que, en los sólidos moleculares, la capacidad calorífica por mol de moléculas normalmente será cercana a 3nR, donde n es el número de átomos por molécula.
Así, n átomos de un sólido deberían, en principio, almacenar el doble de energía que n átomos de un gas monoatómico. Una forma de ver este resultado es observar que el gas monoatómico sólo puede almacenar energía como energía cinética de los átomos, mientras que el sólido también puede almacenarla como energía potencial de los enlaces tensados por las vibraciones. La capacidad calorífica átomo-molar de un gas poliatómico se acerca a la de un sólido a medida que aumenta el número n de átomos por molécula.
Como en el caso de los gases, algunos de los modos de vibración quedarán "congelados" a bajas temperaturas, especialmente en sólidos con átomos ligeros y fuertemente unidos, provocando que la capacidad calorífica átomo-molar sea menor que este límite teórico. De hecho, la capacidad calorífica átomo-molar (o específica) de una sustancia sólida tiende a cero a medida que la temperatura se acerca al cero absoluto.
Ley Dulong–Petit
Como predijo el análisis anterior, la capacidad calorífica por mol de átomos, en lugar de por mol de moléculas, resulta notablemente constante para todas las sustancias sólidas a altas temperaturas. Esta relación se observó empíricamente en 1819 y se denomina ley de Dulong-Petit, en honor a sus dos descubridores. Este descubrimiento fue un argumento importante en apoyo de la teoría atómica de la materia.
De hecho, para elementos químicos metálicos sólidos a temperatura ambiente, las capacidades caloríficas átomo-molar varían de aproximadamente 2,8 R a 3,4 R. Grandes excepciones en el extremo inferior involucran sólidos compuestos de átomos estrechamente unidos y de masa relativamente baja, como el berilio (2,0 R, sólo el 66% del valor teórico) y el diamante (0,735 ). R, sólo el 24%). Esas condiciones implican un mayor espaciamiento de energía vibratoria cuántica, por lo que muchos modos vibratorios están "congelados" en el tiempo. a temperatura ambiente. El hielo de agua cerca del punto de fusión también tiene una capacidad calorífica por átomo anormalmente baja (1,5 R, sólo el 50% del valor teórico).
En el extremo superior de las capacidades caloríficas posibles, la capacidad calorífica puede exceder R en cantidades modestas, debido a las contribuciones de las vibraciones anarmónicas en los sólidos y, a veces, a una contribución modesta de los electrones de conducción en los metales. Estos no son grados de libertad tratados en las teorías de Einstein o Debye.
Calor específico de elementos sólidos
Dado que la densidad aparente de un elemento químico sólido está fuertemente relacionada con su masa molar, existe una correlación inversa notable entre la densidad de un sólido y su capacidad calorífica específica en una proporción per- base de masa. Esto se debe a una tendencia muy aproximada de los átomos de la mayoría de los elementos a tener aproximadamente el mismo tamaño, a pesar de variaciones mucho más amplias en densidad y peso atómico. Estos dos factores (constancia del volumen atómico y constancia de la capacidad calorífica específica de un mol) dan como resultado una buena correlación entre el volumen de cualquier elemento químico sólido dado y su capacidad calorífica total.
Otra forma de expresar esto es que la capacidad calorífica específica del volumen (capacidad calorífica volumétrica) de los elementos sólidos es aproximadamente una constante. El volumen molar de los elementos sólidos es aproximadamente constante y (aún más confiablemente) también lo es la capacidad calorífica molar de la mayoría de las sustancias sólidas. Estos dos factores determinan la capacidad calorífica volumétrica, que como propiedad del volumen puede tener una consistencia sorprendente. Por ejemplo, el elemento uranio es un metal que tiene una densidad casi 36 veces mayor que la del metal litio, pero la capacidad calorífica específica del uranio en términos volumétricos (es decir, por volumen dado de metal) es sólo un 18% mayor que la del litio. #39;s.
Sin embargo, el volumen atómico promedio en los elementos sólidos no es del todo constante, por lo que existen desviaciones de este principio. Por ejemplo, el arsénico, que es sólo un 14,5% menos denso que el antimonio, tiene casi un 59% más de capacidad calorífica específica en términos de masa. En otras palabras; Aunque un lingote de arsénico es sólo un 17% más grande que uno de antimonio de la misma masa, absorbe alrededor de un 59% más de calor para un aumento de temperatura determinado. Las proporciones de capacidad calorífica de las dos sustancias siguen de cerca las proporciones de sus volúmenes molares (las proporciones de números de átomos en el mismo volumen de cada sustancia); la desviación de la correlación con volúmenes simples, en este caso, se debe a que los átomos de arsénico más ligeros están significativamente más empaquetados que los átomos de antimonio, en lugar de tener un tamaño similar. En otras palabras, átomos de tamaño similar harían que un mol de arsénico fuera un 63% más grande que un mol de antimonio, con una densidad correspondientemente menor, lo que permitiría que su volumen reflejara más fielmente su comportamiento de capacidad calorífica.
Efecto de las impurezas
A veces, pequeñas concentraciones de impurezas pueden afectar en gran medida el calor específico, por ejemplo en aleaciones ferromagnéticas semiconductoras.
Calor específico de los líquidos
Aún no se ha logrado una teoría general de la capacidad calorífica de los líquidos y sigue siendo un área activa de investigación. Durante mucho tiempo se pensó que la teoría de los fonones no podía explicar la capacidad calorífica de los líquidos, ya que los líquidos sólo contienen fonones longitudinales, pero no transversales, que en los sólidos son responsables de 2/3 de la capacidad calorífica. Sin embargo, los experimentos de dispersión de Brillouin con neutrones y rayos X, que confirman una intuición de Yakov Frenkel, han demostrado que los fonones transversales existen en los líquidos, aunque restringidos a frecuencias superiores a un umbral llamado frecuencia de Frenkel. Dado que la mayor parte de la energía está contenida en estos modos de alta frecuencia, una simple modificación del modelo de Debye es suficiente para producir una buena aproximación a las capacidades caloríficas experimentales de líquidos simples.
Debido a las altas energías de unión de los cristales, los efectos de la congelación en modo vibratorio se observan en sólidos con más frecuencia que en líquidos: por ejemplo, la capacidad calorífica del agua líquida es el doble que la del hielo casi a la misma temperatura, y nuevamente está cerca de la 3R por mol de átomos del máximo teórico de Dulong-Petit.
Los materiales amorfos pueden considerarse un tipo de líquido a temperaturas superiores a la temperatura de transición vítrea. Por debajo de la temperatura de transición vítrea, los materiales amorfos se encuentran en estado sólido (vítreo). El calor específico tiene discontinuidades características en la temperatura de transición vítrea que se deben a la ausencia en el estado vítreo de cúmulos de enlaces rotos (configuraciones) que se filtran y que sólo están presentes en la fase líquida. Por encima de la temperatura de transición vítrea, los grupos de percolación formados por enlaces rotos permiten una estructura más flexible y, por tanto, un mayor grado de libertad para el movimiento atómico, lo que da como resultado una mayor capacidad calorífica de los líquidos. Por debajo de la temperatura de transición vítrea no hay grupos extendidos de enlaces rotos y la capacidad calorífica es menor porque la estructura de estado sólido (vítreo) del material amorfo es más rígida. Las discontinuidades en la capacidad calorífica se utilizan normalmente para detectar la temperatura de transición vítrea donde un líquido sobreenfriado se transforma en vidrio.
Efecto de los enlaces de hidrógeno
Las moléculas polares que contienen hidrógeno, como el etanol, el amoníaco y el agua, tienen poderosos enlaces de hidrógeno intermoleculares cuando están en su fase líquida. Estos enlaces proporcionan otro lugar donde se puede almacenar calor como energía potencial de vibración, incluso a temperaturas comparativamente bajas. Los enlaces de hidrógeno explican el hecho de que el agua líquida almacena casi el límite teórico de 3R por mol de átomos, incluso a temperaturas relativamente bajas (es decir, cerca del punto de congelación del agua).
