Capa límite

La capa de límite alrededor de una mano humana, fotografía Schlieren. La capa de límite es la frontera verde brillante, más visible en la parte posterior de la mano (clic para imagen de alta resistencia).

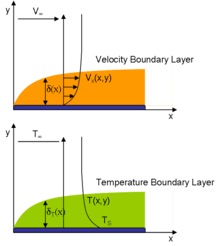
En física y mecánica de fluidos, una capa límite es la capa delgada de fluido en la vecindad inmediata de una superficie límite formada por el fluido que fluye a lo largo de la superficie. La interacción del fluido con la pared induce una condición de contorno sin deslizamiento (velocidad cero en la pared). Luego, la velocidad del flujo aumenta monótonamente por encima de la superficie hasta que vuelve a la velocidad del flujo total. La capa delgada que consiste en fluido cuya velocidad aún no ha vuelto a la velocidad de flujo a granel se denomina capa límite de velocidad.

El aire junto a un ser humano se calienta, lo que da como resultado un flujo de aire convectivo inducido por la gravedad, flujo de aire que da como resultado una capa límite térmica y de velocidad. Una brisa rompe la capa límite, y el cabello y la ropa la protegen, haciendo que el ser humano se sienta más fresco o más cálido. En el ala de un avión, la capa límite de velocidad es la parte del flujo cercana al ala, donde las fuerzas viscosas distorsionan el flujo no viscoso circundante. En la atmósfera terrestre, la capa límite atmosférica es la capa de aire (~ 1 km) cerca del suelo. Se ve afectado por la superficie; flujos de calor día-noche causados por el sol que calienta el suelo, la humedad o la transferencia de cantidad de movimiento hacia o desde la superficie.

Tipos de capa límite

Visualización de la capa liviana, mostrando transición de la condición laminar a la turbulenta

Las capas límite laminares se pueden clasificar libremente según su estructura y las circunstancias en las que se crean. La delgada capa de corte que se desarrolla en un cuerpo oscilante es un ejemplo de una capa límite de Stokes, mientras que la capa límite de Blasius se refiere a la conocida solución de similitud cerca de una placa plana adjunta que se mantiene en un flujo unidireccional que se aproxima y la capa límite de Falkner-Skan. una generalización del perfil de Blasius. Cuando un fluido gira y las fuerzas viscosas se equilibran mediante el efecto de Coriolis (en lugar de la inercia convectiva), se forma una capa de Ekman. En la teoría de la transferencia de calor, se produce una capa límite térmica. Una superficie puede tener múltiples tipos de capa límite simultáneamente.

La naturaleza viscosa del flujo de aire reduce las velocidades locales en una superficie y es responsable de la fricción de la piel. La capa de aire sobre la superficie del ala que se ralentiza o se detiene por la viscosidad, es la capa límite. Hay dos tipos diferentes de flujo de capa límite: laminar y turbulento.

Flujo laminar de la capa límite

El límite laminar es un flujo muy uniforme, mientras que la capa límite turbulenta contiene remolinos o "remolinos". El flujo laminar genera menos arrastre por fricción superficial que el flujo turbulento, pero es menos estable. El flujo de la capa límite sobre la superficie de un ala comienza como un flujo laminar suave. A medida que el flujo continúa retrocediendo desde el borde de ataque, la capa límite laminar aumenta de espesor.

Flujo turbulento de la capa límite

A cierta distancia del borde de ataque, el flujo laminar uniforme se descompone y pasa a ser un flujo turbulento. Desde el punto de vista de la resistencia aerodinámica, es aconsejable tener la transición de flujo laminar a turbulento lo más atrás posible del ala, o tener una gran parte de la superficie del ala dentro de la porción laminar de la capa límite. Sin embargo, el flujo laminar de baja energía tiende a romperse más repentinamente que la capa turbulenta.

El concepto de capa límite de Prandtl

Ludwig Prandtl

Perfil de velocidad de capa de límite laminar

La primera hipótesis sobre la capa límite aerodinámica fue Ludwig Prandtl en un artículo presentado el 12 de agosto de 1904 en el tercer Congreso Internacional de Matemáticos en Heidelberg, Alemania. Simplifica las ecuaciones del flujo de fluidos al dividir el campo de flujo en dos áreas: una dentro de la capa límite, dominada por la viscosidad y que crea la mayor parte del arrastre experimentado por el cuerpo límite; y uno fuera de la capa límite, donde la viscosidad puede despreciarse sin efectos significativos en la solución. Esto permite una solución de forma cerrada para el flujo en ambas áreas al realizar simplificaciones significativas de las ecuaciones completas de Navier-Stokes. La misma hipótesis es aplicable a otros fluidos (además del aire) con una viscosidad de moderada a baja, como el agua. En el caso de que haya una diferencia de temperatura entre la superficie y el fluido a granel, se encuentra que la mayor parte de la transferencia de calor hacia y desde un cuerpo tiene lugar en la vecindad de la capa límite de velocidad. Esto nuevamente permite que las ecuaciones se simplifiquen en el campo de flujo fuera de la capa límite. La distribución de la presión a lo largo de la capa límite en la dirección normal a la superficie (como un perfil aerodinámico) permanece relativamente constante en toda la capa límite y es la misma que en la superficie misma.

El grosor de la capa límite de velocidad normalmente se define como la distancia desde el cuerpo sólido hasta el punto en el que la velocidad del flujo viscoso es el 99 % de la velocidad de la corriente libre (la velocidad superficial de un flujo no viscoso). El espesor de desplazamiento es una definición alternativa que establece que la capa límite representa un déficit en el flujo másico en comparación con el flujo no viscoso con deslizamiento en la pared. Es la distancia que tendría que desplazarse la pared en el caso no viscoso para dar el mismo flujo de masa total que en el caso viscoso. La condición de no deslizamiento requiere que la velocidad del flujo en la superficie de un objeto sólido sea cero y que la temperatura del fluido sea igual a la temperatura de la superficie. La velocidad del flujo aumentará rápidamente dentro de la capa límite, regida por las ecuaciones de la capa límite, a continuación.

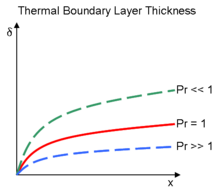
El espesor de la capa límite térmica es similar a la distancia desde el cuerpo a la que la temperatura es el 99 % de la temperatura de la corriente libre. La relación de los dos espesores se rige por el número de Prandtl. Si el número de Prandtl es 1, las dos capas límite tienen el mismo espesor. Si el número de Prandtl es mayor que 1, la capa límite térmica es más delgada que la capa límite de velocidad. Si el número de Prandtl es inferior a 1, que es el caso del aire en condiciones estándar, la capa límite térmica es más gruesa que la capa límite de velocidad.

En diseños de alto rendimiento, como planeadores y aviones comerciales, se presta mucha atención al control del comportamiento de la capa límite para minimizar la resistencia. Hay que considerar dos efectos. En primer lugar, la capa límite se suma al espesor efectivo del cuerpo, a través del espesor de desplazamiento, aumentando así la resistencia a la presión. En segundo lugar, las fuerzas de cizallamiento en la superficie del ala crean un arrastre por fricción superficial.

Con números de Reynolds altos, típicos de aviones de tamaño completo, es deseable tener una capa límite laminar. Esto da como resultado una menor fricción superficial debido al perfil de velocidad característico del flujo laminar. Sin embargo, la capa límite inevitablemente se espesa y se vuelve menos estable a medida que el flujo se desarrolla a lo largo del cuerpo, y eventualmente se vuelve turbulento, el proceso conocido como transición de la capa límite. Una forma de solucionar este problema es succionar la capa límite a través de una superficie porosa (ver Succión de la capa límite). Esto puede reducir la resistencia, pero generalmente no es práctico debido a su complejidad mecánica y la potencia requerida para mover el aire y eliminarlo. Las técnicas de flujo laminar natural (NLF) empujan la transición de la capa límite hacia atrás remodelando el perfil aerodinámico o el fuselaje para que su punto más grueso sea más hacia atrás y menos grueso. Esto reduce las velocidades en la parte delantera y se logra el mismo número de Reynolds con una mayor longitud.

Con números de Reynolds más bajos, como los que se observan con modelos de aviones, es relativamente fácil mantener el flujo laminar. Esto proporciona una baja fricción en la piel, lo cual es deseable. Sin embargo, el mismo perfil de velocidad que le da a la capa límite laminar su baja fricción superficial también hace que se vea gravemente afectada por gradientes de presión adversos. A medida que la presión comienza a recuperarse sobre la parte trasera de la cuerda del ala, una capa límite laminar tenderá a separarse de la superficie. Tal separación del flujo provoca un gran aumento en la resistencia a la presión, ya que aumenta en gran medida el tamaño efectivo de la sección del ala. En estos casos, puede ser ventajoso hacer que la capa límite entre en turbulencia deliberadamente en un punto anterior a la ubicación de la separación laminar, utilizando un turbulador. El perfil de velocidad más completo de la capa límite turbulenta le permite sostener el gradiente de presión adverso sin separarse. Por lo tanto, aunque aumenta la fricción superficial, disminuye la resistencia general. Este es el principio detrás de los hoyuelos en las pelotas de golf, así como en los generadores de vórtices en los aviones. También se han diseñado secciones de ala especiales que adaptan la recuperación de presión para reducir o incluso eliminar la separación laminar. Esto representa un compromiso óptimo entre el arrastre de presión de la separación del flujo y la fricción superficial de la turbulencia inducida.

Al usar semimodelos en túneles de viento, a veces se usa un peniche para reducir o eliminar el efecto de la capa límite.

Ecuaciones de capa límite

La deducción de las ecuaciones de la capa límite fue uno de los avances más importantes en dinámica de fluidos. Usando un análisis de orden de magnitud, las conocidas ecuaciones de Navier-Stokes que gobiernan el flujo de fluido viscoso se pueden simplificar en gran medida dentro de la capa límite. En particular, la característica de las ecuaciones diferenciales parciales (PDE) se vuelve parabólica, en lugar de la forma elíptica de las ecuaciones completas de Navier-Stokes. Esto simplifica enormemente la solución de las ecuaciones. Al hacer la aproximación de la capa límite, el flujo se divide en una parte no viscosa (que es fácil de resolver mediante varios métodos) y la capa límite, que se rige por una PDE más fácil de resolver. Las ecuaciones de continuidad y de Navier-Stokes para un flujo incompresible estacionario bidimensional en coordenadas cartesianas están dadas por

∂ ∂ u∂ ∂ x+∂ ∂ .. ∂ ∂ Sí.=0{displaystyle {partial u over partial x}+{partial upsilon over partial y}=0}

u∂ ∂ u∂ ∂ x+.. ∂ ∂ u∂ ∂ Sí.=− − 1*** *** ∂ ∂ p∂ ∂ x+.. ()∂ ∂ 2u∂ ∂ x2+∂ ∂ 2u∂ ∂ Sí.2){displaystyle u{partial u over partial x}+upsilon {partial u over partial y}=-{1 over rho }{partial pover partial x}+nu }left({2}u over partial x^{2}}}}{u}{2}{}{u}{}{}}{2}}{}}}}}}}{}{}}}{}{}}}{}{}}}}}}{}{}{}{}}}}}}{}{}}}}}}}}}}}}}}}}}}}}}}}}}}}}{}{}}}}}{}}}}}}}}}}}}}{}}}}}}}}}}}{}{}}}}}}}}}}}}}}}{}}}}}}}{}}}}}{}{}}}}}}}}}

u∂ ∂ .. ∂ ∂ x+.. ∂ ∂ .. ∂ ∂ Sí.=− − 1*** *** ∂ ∂ p∂ ∂ Sí.+.. ()∂ ∂ 2.. ∂ ∂ x2+∂ ∂ 2.. ∂ ∂ Sí.2){displaystyle u{partial upsilon over partial x}+upsilon {partial upsilon over partial y}=-{1 over rho }{partial p over partial y}+{nu }partial ^ {2}upsilon over}{2}{}{upcial2} {}{}{}{}{}{}{}{}{}{2}{}{}{partial}{}{}{}{}{}{}{}{}{}{}{}{}{partial}}}}}}}}{}{}{}}}}{}{}{}{}}}}}}}}}}}}}}{}{}{}}{}}}}}}{}}}}}}}}}}{}}}}}}}{}}}}}}{}}}}}{}{}}}}}{}{}

Donde u{displaystyle u} y .. {displaystyle upsilon } son los componentes de velocidad, *** *** {displaystyle rho } es la densidad, p{displaystyle p} es la presión, y .. {displaystyle nu } es la viscosidad cinemática del fluido en un punto.

La aproximación indica que, para un número suficientemente alto de Reynolds el flujo sobre una superficie puede dividirse en una región exterior de flujo invisivo no afectada por la viscosidad (la mayoría del flujo), y una región cercana a la superficie donde la viscosidad es importante (la capa de límite). Vamos u{displaystyle u} y .. {displaystyle upsilon } ser velocidades transversas y transversales, respectivamente, dentro de la capa de límites. Mediante el análisis de escala, se puede demostrar que las ecuaciones anteriores del movimiento reducen dentro de la capa de límites para convertirse

u∂ ∂ u∂ ∂ x+.. ∂ ∂ u∂ ∂ Sí.=− − 1*** *** ∂ ∂ p∂ ∂ x+.. ∂ ∂ 2u∂ ∂ Sí.2{displaystyle u{partial u over partial x}+upsilon {partial u over partial y}=-{1 over rho }{partial pover partial x}+nu }{2}u over partial y^{2}}}}}}} {displaystyle u{partial u{2}}}}}}}} {

1*** *** ∂ ∂ p∂ ∂ Sí.=0{displaystyle {1 over rho }{partial p over partial y}=0}

y si el fluido es incompresible (como lo son los líquidos en condiciones estándar):

∂ ∂ u∂ ∂ x+∂ ∂ .. ∂ ∂ Sí.=0{displaystyle {partial u over partial x}+{partial upsilon over partial y}=0}

El análisis de orden de magnitud asume la escala de longitud de la secuencia significativamente mayor que la escala de longitud transversal dentro de la capa de límite. Se sigue que las variaciones en las propiedades en la dirección de la secuencia son generalmente mucho más bajas que las de la pared dirección normal. Aplicar esto a la ecuación de continuidad muestra que .. {displaystyle upsilon }, la velocidad normal de la pared, es pequeña en comparación con u{displaystyle u} la velocidad de transmisión.

Desde la presión estática p{displaystyle p} es independiente de Sí.{displaystyle y}, entonces la presión en el borde de la capa de límite es la presión a lo largo de la capa de límite en una posición de secuencia dada. La presión externa puede obtenerse a través de una aplicación de la ecuación de Bernoulli. Vamos U{displaystyle U} ser la velocidad del fluido fuera de la capa de límite, donde u{displaystyle u} y U{displaystyle U} ambos son paralelos. Esto da lugar a la sustitución p{displaystyle p} el resultado siguiente

u∂ ∂ u∂ ∂ x+.. ∂ ∂ u∂ ∂ Sí.=UdUdx+.. ∂ ∂ 2u∂ ∂ Sí.2{displaystyle u{partial u over partial x}+upsilon {partial u over partial Y... {fn} {fn} {fn} {c}uover partial y^{2}}}

Para un flujo en el cual la presión estática p{displaystyle p} tampoco cambia en la dirección del flujo

dpdx=0{displaystyle {fnK}=0}

Así que... U{displaystyle U} permanece constante.

Por lo tanto, la ecuación de movimiento se simplifica para convertirse en

u∂ ∂ u∂ ∂ x+.. ∂ ∂ u∂ ∂ Sí.=.. ∂ ∂ 2u∂ ∂ Sí.2{displaystyle u{partial u over partial x}+upsilon {partial u over partial y}={nu }{partial ^{2}u over partial y^{2}}} {}}} {

Estas aproximaciones se utilizan en una variedad de problemas prácticos de flujo de interés científico y de ingeniería. El análisis anterior es para cualquier capa límite instantánea laminar o turbulenta, pero se usa principalmente en estudios de flujo laminar ya que el flujo medio es también el flujo instantáneo porque no hay fluctuaciones de velocidad presentes. Esta ecuación simplificada es una PDE parabólica y se puede resolver utilizando una solución de similitud a menudo denominada capa límite de Blasius.

Teorema de transposición de Prandtl

Prandtl observó que desde cualquier solución u()x,Sí.,t),v()x,Sí.,t){displaystyle u(x,y,t), v(x,y,t)} que satisface las ecuaciones de la capa fronteriza, solución más uAlternativa Alternativa ()x,Sí.,t),vAlternativa Alternativa ()x,Sí.,t){displaystyle u^{*}(x,y,t), v^{*}(x,y,t)}, que también está satisfaciendo las ecuaciones de capa de límites, se puede construir por escrito

uAlternativa Alternativa ()x,Sí.,t)=u()x,Sí.+f()x),t),vAlternativa Alternativa ()x,Sí.,t)=v()x,Sí.+f()x),t)− − f.()x)u()x,Sí.+f()x),t){displaystyle u^{*}(x,y,t)=u(x,y+f(x),t),quad v^{*}(x,y,t)=v(x,y+f(x),t)-f'(x)u(x,y+f(x),t)}

Donde f()x){displaystyle f(x)} es arbitrario. Puesto que la solución no es única desde la perspectiva matemática, a la solución puede agregar cualquiera de un conjunto infinito de funciones eigen como muestra Stewartson y Paul A. Libby.

Integral de cantidad de movimiento de Von Kármán

Von Kármán derivó la ecuación integral al integrar la ecuación de la capa límite a través de la capa límite en 1921. La ecuación es

τ τ w*** *** U2=1U2∂ ∂ ∂ ∂ t()Uδ δ 1)+∂ ∂ δ δ 2∂ ∂ x+2δ δ 2+δ δ 1U∂ ∂ U∂ ∂ x+vwU{displaystyle {fnMicroc {fnMicroc}tau ¿Qué? U^{2}={frac {1} {fn} {fn} {fnK} {f}} {f}} {fn}} {fn}} {fn}} {fn}} {fn}} {fn}}} {f}} {f}}} {f}}}} {f}}}} {f}}} {f} {f}}}} {f}}} {f}} {f} {f}} {f}} {f}}f}} {f} {f} {f} {f}}f}}}}}}}} {f} {f}}} {f} {f}}} {f}} {f} {f}} {f}f}f}f}}}}f}}}}}}}}f}f}}f}f}}}f}}}}}}}}}} ¿Por qué? {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} ###{frac {2delta _{2}+delta {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} x}+{frac {fnK}} {fnK}} {fnK}}}}} {f}}}}} {f}}}} {f}}}}}} {f}}}}}}}}}}} {f}}}}}}}}}} {f} {f}}}}}}} {f}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

dónde

τ τ w=μ μ ()∂ ∂ u∂ ∂ Sí.)Sí.=0,vw=v()x,0,t),δ δ 1=∫ ∫ 0JUEGO JUEGO ()1− − uU)dSí.,δ δ 2=∫ ∫ 0JUEGO JUEGO uU()1− − uU)dSí.{displaystyle tau _{w}=muleft({frac {partial u}{partial y}}right)_{y=0},quad v_{w}=v(x,0,t),quad delta ¿Qué? ¿Por qué? ¿Qué? ¿Qué?

τ τ w{displaystyle tau _{w} es el estrés de la pared, vw{displaystyle ¿Qué? es la velocidad de succión/inyección en la pared, δ δ 1{displaystyle delta ¿Qué? es el espesor del desplazamiento y δ δ 2{displaystyle delta _{2} es el espesor del impulso. Kármán-Pohlhausen La aproximación se deriva de esta ecuación.

Energía integral

La integral de energía fue derivada por Wieghardt.

2ε ε *** *** U3=1U∂ ∂ ∂ ∂ t()δ δ 1+δ δ 2)+2δ δ 2U2∂ ∂ U∂ ∂ t+1U3∂ ∂ ∂ ∂ x()U3δ δ 3)+vwU{displaystyle {frac {2varepsilon ♪♪ U^{3}={frac {0} {f} {f} {f} {f}} {f}} {f}} {f}} {f}} {f}}} {f}}} {f}}} {f}}} {f}}} {f}} {f}} {f}f}f}} {f} {f}}} {f}}}}} {f} {f} {f}} {f}f}}}}f} {f}f} {f} {f} {f} {f}f}f} {f}}f}f}f}f}f}f}f}f}}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f} _{1}+delta - ¿Qué? {fnK} {fnK} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {f}} {fnMicrosoft}} {f}} {fnMicrosoft}} {fnMicrosoft}}}} {f} {fnMicroc}}}} {f}}} {f}} {f}}}} {f}}}}}}}}}}}}}}}}}} {f} {f}f}f} {f} {f} {f} {f}f} {f}f}f}f}}f}f}f}f}f}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}}fn t}+{frac {1} {fn} {fnK}} {fnMicroc}} {fn}}} {f}} {f}}} {fn}}} {f}}} {fn}}}} {fn}}}} {fnMicroc}}}}}} {f}}}} {f} {f}} {f}}}}} {f}}}}}} {f}} {f} {f}} {f} {f}}} {f}}} {f} {f}}} {f}}} {f} {f} {f}}} {f}} {f} {f}}}}} {f}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}f}}}}}}}}} {partial }{partial ♪♪ _{3})+{frac {fnK}} {fnK}} {fnK}}}}} {f}}}}} {f}}}} {f}}}}}} {f}}}}}}}}}}} {f}}}}}}}}}} {f} {f}}}}}}} {f}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

dónde

ε ε =∫ ∫ 0JUEGO JUEGO μ μ ()∂ ∂ u∂ ∂ Sí.)2dSí.,δ δ 3=∫ ∫ 0JUEGO JUEGO uU()1− − u2U2)dSí.{displaystyle varepsilon =int _{0}{infty }mu left({frac {partial u}{partial y}}right)}{2}y,quad delta ¿Qué? ¿Qué? {U}left(1-{u^{2}}right),dy}

ε ε {displaystyle varepsilon } es la tasa de disipación de energía debido a la viscosidad a través de la capa fronteriza y δ δ 3{displaystyle delta ¿Qué? es el espesor de la energía.

Transformación de Von Mises

Para capas de límites estables bidimensionales, von Mises introdujo una transformación que toma x{displaystyle x} y ↑ ↑ {displaystyle psi }(función de corriente) como variables independientes en lugar de x{displaystyle x} y Sí.{displaystyle y} y utiliza una variable dependiente χ χ =U2− − u2{displaystyle chi =U^{2}-u^{2} en lugar de u{displaystyle u}. La ecuación de la capa de límites se convierte en

∂ ∂ χ χ ∂ ∂ x=.. U2− − χ χ ∂ ∂ 2χ χ ∂ ∂ ↑ ↑ 2{fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} chi }{partial #=nu {sqrt {fnMicroc {partial ^{2}chi}{chi}{partial psi ^{2}}}

Las variables originales se recuperan de

Sí.=∫ ∫ U2− − χ χ d↑ ↑ ,u=U2− − χ χ ,v=u∫ ∫ ∂ ∂ ∂ ∂ x()1u)d↑ ↑ .{displaystyle y=int {sqrt {U^{2}-chi },dpsiquad u={sqrt {U^{2}-chi }}quad v=uint {fnMicroc {fnMicrosoft Sans Serif} {fnMicroc {fnMicrosoft Sans Serif}dpsi.}

Esta transformación se extiende posteriormente a la capa límite compresible por von Kármán y HS Tsien.

La transformación de Crocco

Para una capa de límites compresibles estable, Luigi Crocco introdujo una transformación que toma x{displaystyle x} y u{displaystyle u} como variables independientes en lugar de x{displaystyle x} y Sí.{displaystyle y} y utiliza una variable dependiente τ τ =μ μ ∂ ∂ u/∂ ∂ Sí.{displaystyle tau =mu partial u/partial y}(estrés de la vista) en lugar de u{displaystyle u}. La ecuación de la capa de límite entonces se convierte

μ μ *** *** u∂ ∂ ∂ ∂ x()1τ τ )+∂ ∂ 2τ τ ∂ ∂ u2− − μ μ dpdx∂ ∂ ∂ ∂ u()1τ τ )=0,sidpdx=0,entoncesμ μ *** *** τ τ 2∂ ∂ τ τ ∂ ∂ x=1u∂ ∂ 2τ τ ∂ ∂ u2.{displaystyle {begin{aligned} {murho u{frac {partial }left({frac {1}{tau }right)+frac {partial ^{2}tau }{partial u^{2}}}}}}mu {fnMicroc} {fnMicroc} {fnMicroc}} {fnMicroc}} {f}} {fnMicroc}}} {fnMicroc}} {fnMicroc}} {f}}}} {f}}} {fnMicroc} {fnK} {f} {f} {fnh}}fnh}}=0,[5pt] âtext{if}{if}{frac {dp}}=0,{text{} {f} {f} {f} {f} {f} {c} {c} {c} {c}}}}} {c}}}}} {c}}} {c}} {c}}}}}} {c} {c}}}}} {c}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}}}} {f} {f}} {f}}}}} {f}f} {f} {f}f} {f}}f}}}}}}}}}}f} {f}f}}}}}}}}}}}}}}}}} {fnMicroc {}} {fnMicroc {partial }tau }{partial u^{2}}}}}end{aligned}}}}

La coordenada original se recupera de

Sí.=μ μ ∫ ∫ duτ τ .{displaystyle y=mu int {frac {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}} {fn}} {fn}}} {f}}} {fn}} {fnK}} {f}} {f}} {f}}}}} {fnf}}}} {tau}} {tau}}}}}}}}}}}}}} {tau}}}} {tau}}}} {tau}}}}} {tau} {tau}}}}} {tau}}}}}}}}}}}}}}}}}} {tau} {tau}} {tau}}} {tau}}} {tau}}}}}}}}}}}}}}} {tau}} {tau}}}}}}}}}}}}}}}}}}}}}}}} }}

Capas límite turbulentas

El tratamiento de las capas límite turbulentas es mucho más difícil debido a la variación de las propiedades del flujo que depende del tiempo. Una de las técnicas más utilizadas para abordar los flujos turbulentos es aplicar la descomposición de Reynolds. Aquí, las propiedades del flujo instantáneo se descomponen en un componente medio y fluctuante con la suposición de que la media del componente fluctuante es siempre cero. La aplicación de esta técnica a las ecuaciones de la capa límite proporciona las ecuaciones completas de la capa límite turbulenta que no se dan a menudo en la literatura:

∂ ∂ ū ̄ ∂ ∂ x+∂ ∂ v̄ ̄ ∂ ∂ Sí.=0{displaystyle {partial {overline {u}over partial x}+{partial {overline {v}over partial y}=0}} {b}}} {cH}} {cH}}}} {b}}}}}}}} {b}}}}}}}}}} {b}}}}} {

ū ̄ ∂ ∂ ū ̄ ∂ ∂ x+v̄ ̄ ∂ ∂ ū ̄ ∂ ∂ Sí.=− − 1*** *** ∂ ∂ p̄ ̄ ∂ ∂ x+.. ()∂ ∂ 2ū ̄ ∂ ∂ x2+∂ ∂ 2ū ̄ ∂ ∂ Sí.2)− − ∂ ∂ ∂ ∂ Sí.()u.v.̄ ̄ )− − ∂ ∂ ∂ ∂ x()u.2̄ ̄ ){displaystyle {overline {u}{partial {overline {u}} {f}} {f}} {fn}}} {fn}}}} {fnK}}}} {fnK}}}}}} {f}}}} {f}}}}}}}}}}}} {b9}}}}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {c} {c} {c}} {c} {c} {c} {c}c} {c}c} {c}c}cc} {c}}cccc}c}c}cc}c}cc}c}c}c}c}c}c}ccc}ccccccccc}c}c}c}ccc}c}cccc}cccccccc}c}ccc}c}c}ccc}ccc}cc}c}c}c

ū ̄ ∂ ∂ v̄ ̄ ∂ ∂ x+v̄ ̄ ∂ ∂ v̄ ̄ ∂ ∂ Sí.=− − 1*** *** ∂ ∂ p̄ ̄ ∂ ∂ Sí.+.. ()∂ ∂ 2v̄ ̄ ∂ ∂ x2+∂ ∂ 2v̄ ̄ ∂ ∂ Sí.2)− − ∂ ∂ ∂ ∂ x()u.v.̄ ̄ )− − ∂ ∂ ∂ ∂ Sí.()v.2̄ ̄ ){c} {c} {c} {c} {c} {c}}} {c}} {c} {c}} {c} {c}} {cc} {c}} {cc} {c} {c} {c}} {cccc}} {c}}} {ccccc}}}}cccccccccc}cc}ccccccccccccccc}ccc}cccccccccc}ccccccccc}c}ccc}c}cccc}cc}cccc}c}c

Utilizando un análisis similar de orden-de-magnitud, las ecuaciones anteriores se pueden reducir a términos de orden líderes. Al elegir escalas de longitud δ δ {displaystyle delta } para los cambios en la dirección transversal, y L{displaystyle L. para los cambios en la dirección de secuencia, con <math alttext="{displaystyle delta <δ δ ..L{displaystyle delta.<img alt="delta <, la ecuación x-momentum simplifica a:

ū ̄ ∂ ∂ ū ̄ ∂ ∂ x+v̄ ̄ ∂ ∂ ū ̄ ∂ ∂ Sí.=− − 1*** *** ∂ ∂ p̄ ̄ ∂ ∂ x− − ∂ ∂ ∂ ∂ Sí.()u.v.̄ ̄ ).{displaystyle {overline {u}{partial {overline {u}} {f}} {f}} {fn}}} {fn}}}} {fnK}}}} {fnK}}}}}} {f}}}} {f}}}}}}}}}}}} {b9}}}}} over partial x}+{overline {v}{partial {overline {u} over partial y}=-{1 over rho }{partial {overline {p}over partial x}-{frac {partial }{partial y}}} {overline {u'v'}}}}}}}} {over over over over over over over over }}}}}}}}}}}}}}}}}}}}}}}}} {

Esta ecuación no satisface la condición de no-slip en la pared. Al igual que Prandtl hizo por sus ecuaciones de capa de límites, se debe utilizar una nueva escala de longitud más pequeña para permitir que el término viscoso se convierta en orden líder en la ecuación de impulso. Por elegir <math alttext="{displaystyle eta <.. ..δ δ {displaystyleeta }<img alt="eta < como Sí.- escala, la ecuación de impulso de orden líder para esta "capa de límite interior" es dada por:

0=− − 1*** *** ∂ ∂ p̄ ̄ ∂ ∂ x+.. ∂ ∂ 2ū ̄ ∂ ∂ Sí.2− − ∂ ∂ ∂ ∂ Sí.()u.v.̄ ̄ ).{displaystyle 0=-{1 over rho }{partial {overline {p} over partial x}+{nu }{partial ^{2}{overline {u}over partial y^{2}}-{frac {partial }{partial y}}}} {overline {u'v'}}}}}}}}}}} {}}}}}}} {\\\\\\\\\\\\\\]}}}}}}}}}}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\p1p1p1p1p1p1\p1p1p1p1p1p1p

En el límite del número infinito de Reynolds, se puede demostrar que el término gradiente de presión no tiene efecto en la región interior de la capa de límite turbulento. La nueva "escala de longitud interna" .. {displaystyle eta } es una escala de longitud viscosa, y es de orden .. uAlternativa Alternativa {displaystyle {frac} }{u_{*}}}, con uAlternativa Alternativa {displaystyle U_{*} siendo la escala de velocidad de las fluctuaciones turbulentas, en este caso una velocidad de fricción.

A diferencia de las ecuaciones de la capa límite laminar, la presencia de dos regímenes gobernados por diferentes conjuntos de escalas de flujo (es decir, la escala interna y externa) ha hecho que encontrar una solución de similitud universal para la capa límite turbulenta sea difícil y controvertido. Para encontrar una solución de similitud que abarque ambas regiones del flujo, es necesario igualar asintóticamente las soluciones de ambas regiones del flujo. Dicho análisis producirá la llamada ley logarítmica o ley potencial.

También se han aplicado enfoques similares al análisis anterior para las capas límite térmicas, utilizando la ecuación de energía en flujos compresibles.

El mandato adicional u.v.̄ ̄ {displaystyle {fnMicrosoft Sans Serif}} en las ecuaciones de capa de límites turbulentos se conoce como el estrés de esquila Reynolds y es desconocido a priori. Por lo tanto, la solución de las ecuaciones de capas de límites turbulentos requiere el uso de un modelo de turbulencia, que tiene como objetivo expresar el estrés de esquila de Reynolds en términos de variables de flujo conocidas o derivados. La falta de precisión y generalidad de estos modelos es un obstáculo importante en la predicción exitosa de las propiedades de flujo turbulento en la dinámica de fluidos modernos.

Existe una capa de tensión constante en la región cercana a la pared. Debido a la amortiguación de las fluctuaciones de la velocidad vertical cerca de la pared, el término de tensión de Reynolds se volverá insignificante y encontramos que existe un perfil de velocidad lineal. Esto solo es cierto para la región de la pared muy cercana.

Transferencia de calor y masa

En 1928, el ingeniero francés André Lévêque observó que la transferencia de calor por convección en un fluido en movimiento se ve afectada únicamente por los valores de velocidad muy cercanos a la superficie. Para flujos de gran número de Prandtl, la transición de temperatura/masa desde la superficie hasta la temperatura de la corriente libre tiene lugar en una región muy delgada cerca de la superficie. Por lo tanto, las velocidades de los fluidos más importantes son aquellas dentro de esta región muy delgada en la que el cambio de velocidad puede considerarse lineal con la distancia normal desde la superficie. De esta manera, por

u()Sí.)=U[1− − ()Sí.− − h)2h2]=USí.h[2− − Sí.h],{displaystyle u(y)=Uleft[1-{frac {(y-h)}{h^{2}}}right]=U{frac {y} {h}left[2-{frac} {y} {h}right];,}

cuando Sí.→ → 0{displaystyle yrightarrow 0}, entonces

u()Sí.).. 2USí.h=Silencio Silencio Sí.,{displaystyle u(y)approx 2U{frac {y}=theta y,}

donde θ es la tangente de la parábola de Poiseuille que corta la pared. Aunque la solución de Lévêque era específica para la transferencia de calor en un flujo de Poiseuille, su conocimiento ayudó a otros científicos a encontrar una solución exacta al problema de la capa límite térmica. Schuh observó que en una capa límite, u es nuevamente una función lineal de y, pero que en este caso, la tangente de la pared es una función de x. Expresó esto con una versión modificada del perfil de Lévêque,

u()Sí.)=Silencio Silencio ()x)Sí..{displaystyle u(y)=theta (x)y.}

Esto resulta en una muy buena aproximación, incluso para abajo Pr{displaystyle Pr. números, así que solo metales líquidos con Pr{displaystyle Pr. mucho menos de 1 no se puede tratar de esta manera. En 1962, Kestin y Persen publicaron un documento en el que se describen soluciones para la transferencia de calor cuando la capa de límite térmico está contenida enteramente dentro de la capa de impulso y para diversas distribuciones de temperatura de la pared. Para el problema de una placa plana con un salto de temperatura x=x0{displaystyle x=x_{0}, proponen una sustitución que reduce la ecuación parabólica de la capa de límites térmicos a una ecuación diferencial ordinaria. La solución a esta ecuación, la temperatura en cualquier punto del fluido, se puede expresar como una función gamma incompleta. Schlichting propuso una sustitución equivalente que reduce la ecuación de capa de límite térmico a una ecuación diferencial ordinaria cuya solución es la misma función gamma incompleta.

Constantes de transferencia convectivas del análisis de la capa límite

Paul Richard Heinrich Blasius deriva una solución exacta a las ecuaciones de capas laminares anteriores. El espesor de la capa fronteriza δ δ {displaystyle delta } es una función del número Reynolds para el flujo laminar.

δ δ .. 5.0xRe{displaystyle delta approx 5.0{x over {sqrt {Re}}}

δ δ {displaystyle delta } = el espesor de la capa de límite: la región de flujo donde la velocidad es inferior al 99% de la velocidad de campo vJUEGO JUEGO {displaystyle v_{infty}; x{displaystyle x} es la posición a lo largo de la placa semi-infinita, y Re{displaystyle Re. es el número Reynolds dado por *** *** vJUEGO JUEGO x/μ μ {displaystyle rho v_{infty }x/mu } ()*** *** ={displaystyle rho =} densidad y μ μ ={displaystyle mu =} viscosidad dinámica).

La solución de Blasius utiliza condiciones de contorno en forma adimensional:

vx− − vSvJUEGO JUEGO − − vS=vxvJUEGO JUEGO =vSí.vJUEGO JUEGO =0{displaystyle {V_{x}-v_{S} over v_{infty }-v_{S}={v_{x} over v_{infty }={v_{y}=0}aSí.=0{displaystyle y=0}

vx− − vSvJUEGO JUEGO − − vS=vxvJUEGO JUEGO =1{displaystyle {V_{x}-v_{S} over v_{infty }-v_{S}={v_{x} over v_{infty }=1}aSí.=JUEGO JUEGO {displaystyle y=infty} y x=0{displaystyle x=0}

Velocity Boundary Layer (Top, naranja) y Temperature Boundary Layer (Bottom, verde) comparten una forma funcional debido a la similitud en el Momentum/Energy Balances y condiciones de límites.

Tenga en cuenta que en muchos casos, la condición límite no-deslizante sostiene que vS{displaystyle V_{S}, la velocidad del fluido en la superficie de la placa equivale a la velocidad de la placa en todos los lugares. Si el plato no se mueve, entonces vS=0{displaystyle V_{S}=0}. Se requiere una derivación mucho más complicada si se permite el deslizamiento de líquido.

De hecho, la solución de Blasius para el perfil de velocidad laminar en la capa límite sobre una placa semi-infinita se puede extender fácilmente para describir las capas límite térmica y de concentración para la transferencia de calor y masa, respectivamente. En lugar del balance de momento x diferencial (ecuación de movimiento), esto utiliza un balance de energía y masa derivado de manera similar:

Energía: vx∂ ∂ T∂ ∂ x+vSí.∂ ∂ T∂ ∂ Sí.=k*** *** Cp∂ ∂ 2T∂ ∂ Sí.2{displaystyle v_{x}{partial} T over partial x}+v_{y}{partial T over partial y}={k over rho C_{p}{2}T over partial y^{2}}

Misa: vx∂ ∂ cA∂ ∂ x+vSí.∂ ∂ cA∂ ∂ Sí.=DAB∂ ∂ 2cA∂ ∂ Sí.2{displaystyle v_{x}{partial} c_{A} over partial x}+v_{y}{partial c_{A} over partial y}=D_{AB}{2}c_{A} over partial y^{2}}

Para el equilibrio de impulso, viscosidad cinemática .. {displaystyle nu } puede ser considerado como el dinámica. En el balance energético esto es reemplazado por la difusividad térmica α α =k/*** *** CP{displaystyle alpha ={k/rho C_{P}, y por la difusión masiva DAB{displaystyle D_{AB} en el equilibrio de masas. En la difusividad térmica de una sustancia, k{displaystyle k} es su conductividad térmica, *** *** {displaystyle rho } es su densidad y CP{displaystyle C_{P} es su capacidad de calor. Subscript AB denota la difusividad de las especies A difusor en las especies B.

En el supuesto de que α α =DAB=.. {displaystyle alpha =D_{AB}=nu }, estas ecuaciones se vuelven equivalentes al equilibrio de impulso. Así, para el número Prandtl Pr=.. /α α =1{displaystyle Pr=nu /alpha =1} y número de Schmidt Sc=.. /DAB=1{displaystyle Sc=nu /D_{AB}=1} la solución Blasius se aplica directamente.

En consecuencia, esta derivación utiliza una forma relacionada de las condiciones de límites, reemplazando v{displaystyle v} con T{displaystyle T} o cA{displaystyle c_{A} (temperatura absoluta o concentración de especies A). El subscripto S denota una condición de superficie.

vx− − vSvJUEGO JUEGO − − vS=T− − TSTJUEGO JUEGO − − TS=cA− − cAScAJUEGO JUEGO − − cAS=0{displaystyle {V_{x}-v_{S} over v_{infty }-v_{S}={T-T_{S} over T_{infty {}-T_{S}={c_{A}-c_{AS} over c_{Ainfty }-c_{AS}=0}aSí.=0{displaystyle y=0}

vx− − vSvJUEGO JUEGO − − vS=T− − TSTJUEGO JUEGO − − TS=cA− − cAScAJUEGO JUEGO − − cAS=1{displaystyle {V_{x}-v_{S} over v_{infty }-v_{S}={T-T_{S} over T_{infty {}-T_{S}={c_{A}-c_{AS} over c_{Ainfty }-c_{AS}=1}aSí.=JUEGO JUEGO {displaystyle y=infty} y x=0{displaystyle x=0}

Usando la función aerodinámica, Blasius obtuvo la siguiente solución para el esfuerzo cortante en la superficie de la placa.

τ τ 0=()∂ ∂ vx∂ ∂ Sí.)Sí.=0=0.332vJUEGO JUEGO xRe1/2{displaystyle tau _{0}=left({partial v_{x} over partial y}right)_{y=0}=0.332{v_{infty }over x}Re^{1/2}}} {}} {}}}}} {f}}}}} {f}}}}}}}}}

Y a través de las condiciones de contorno, se sabe que

vx− − vSvJUEGO JUEGO − − vS=T− − TSTJUEGO JUEGO − − TS=cA− − cAScAJUEGO JUEGO − − cAS{displaystyle {V_{x}-v_{S} over v_{infty }-v_{S}={T-T_{S} over T_{infty {}-T_{S}={c_{A}-c_{AS} over c_{Ainfty }-c_{AS}}

Tenemos las siguientes relaciones para el flujo de calor/masa fuera de la superficie de la placa

()∂ ∂ T∂ ∂ Sí.)Sí.=0=0.332TJUEGO JUEGO − − TSxRe1/2{displaystyle left({partial T over partial y}right)_{y=0}=0.332{T_{infty }-T_{S} over x}Re^{1/2}

()∂ ∂ cA∂ ∂ Sí.)Sí.=0=0.332cAJUEGO JUEGO − − cASxRe1/2{displaystyle left({partial c_{A} over partial y}right)_{y=0}=0.332{c_{Ainfty }-c_{AS} over x}Re^{1/2}

Así que... Pr=Sc=1{displaystyle Pr=Sc=1}

δ δ =δ δ T=δ δ c=5.0xRe{displaystyle delta =delta ¿Qué? ¿Por qué?

Donde δ δ T,δ δ c{displaystyle delta _{T},delta ¿Qué? son las regiones de flujo donde T{displaystyle T} y cA{displaystyle c_{A} son menos del 99% de sus valores de campo lejano.

Debido a que el número Prandtl de un líquido en particular no es a menudo unidad, el ingeniero alemán E. Polhausen que trabajó con Ludwig Prandtl intentó extender empíricamente estas ecuaciones para solicitar Prل ل 1{displaystyle Prneq 1}. Sus resultados se pueden aplicar Sc{displaystyle Sc. también. Encontró que para Prandtl número mayor de 0.6, el espesor de la capa de límite térmico fue dado aproximadamente por:

Parcela que muestra el grosor relativo en la capa de límite térmico frente a la capa de límites de la velocidad (en rojo) para varios números de Prandtl. Para Pr=1{displaystyle Pr=1}Los dos son iguales.

δ δ δ δ T=Pr1/3{displaystyle {delta over delta ¿Qué?por lo tantoδ δ δ δ c=Sc1/3{displaystyle {delta over delta - Sí.

A partir de esta solución, es posible caracterizar las constantes de transferencia de masa/calor por convección en función de la región del flujo de la capa límite. La ley de conducción de Fourier y la ley de enfriamiento de Newton se combinan con el término de flujo derivado anteriormente y el espesor de la capa límite.

qA=− − k()∂ ∂ T∂ ∂ Sí.)Sí.=0=hx()TS− − TJUEGO JUEGO ){displaystyle {q over A}=-kleft({partial T over partial y}right)_{y=0}=h_{x}(T_{S}-T_{infty })}

hx=0.332kxRex1/2Pr1/3{displaystyle h_{x}=0.332{k over x}Re_{x}{1/2}Pr^{1/3}

Esto da la constante convectiva local hx{displaystyle h_{x} en un punto en el plano semiinfinito. Integrar sobre la longitud de la placa da un promedio

hL=0.664kxReL1/2Pr1/3{displaystyle h_{L}=0.664{k over x}Re_{L}{1/2}Pr^{1/3}

Siguiendo la derivación con términos de transferencia masiva (k{displaystyle k} = constante de transferencia de masa convectiva, DAB{displaystyle D_{AB} = difusividad de las especies A en las especies B, Sc=.. /DAB{displaystyle Sc=nu /D_{AB}), se obtienen las siguientes soluciones:

kx.=0.332DABxRex1/2Sc1/3{displaystyle k'_{x}=0.332{D_{AB} over x}Re_{x}{1/2}Sc^{1/3}

kL.=0.664DABxReL1/2Sc1/3{displaystyle k'_{L}=0.664{D_{AB} over x}Re_{L}{1/2}Sc^{1/3}

Estas soluciones se aplican a flujo laminar con un número de Prandtl/Schmidt superior a 0,6.

Arquitectura naval

Muchos de los principios que se aplican a las aeronaves también se aplican a los barcos, submarinos y plataformas marinas.

Para los barcos, a diferencia de los aviones, se trata de flujos incompresibles, donde el cambio en la densidad del agua es insignificante (un aumento de presión cercano a 1000kPa conduce a un cambio de solo 2-3 kg/m³). Este campo de la dinámica de fluidos se llama hidrodinámica. Un ingeniero de barcos diseña primero para la hidrodinámica y solo después para la fuerza. El desarrollo, la ruptura y la separación de la capa límite se vuelven críticos debido a que la alta viscosidad del agua produce altos esfuerzos de cizallamiento.

Turbina de capa límite

Este efecto se aprovechó en la turbina Tesla, patentada por Nikola Tesla en 1913. Se la conoce como turbina sin álabes porque utiliza el efecto de capa límite y no un fluido que incide sobre los álabes como en una turbina convencional. Las turbinas de capa límite también se conocen como turbina de tipo cohesión, turbina sin álabes y turbina de capa Prandtl (después de Ludwig Prandtl).

Predicción del espesor de la capa límite transitoria en un cilindro mediante análisis dimensional

Mediante el uso de las ecuaciones de fuerza transitorias y viscosas para un flujo cilíndrico se puede predecir el espesor de capa de límite transitorio encontrando el número de Womersley (Nw{displaystyle No.).

Fuerza transitoria = *** *** vw{displaystyle rho vw}

Fuerza viscosa = μ μ vδ δ 12{displaystyle {mu v over delta ¿Qué?

Haciéndolos iguales entre sí da:

*** *** vw=μ μ vδ δ 12{displaystyle rho vw={mu v over delta ¿Qué?

Resolviendo para delta da:

δ δ 1=μ μ *** *** w=vw{displaystyle delta ¿Por qué?

En forma adimensional:

Lδ δ 1=Lwv=Nw{displaystyle {L over delta ¿Qué? L{sqrt {w over over - Sí.

Donde Nw{displaystyle No. = Número de Womersley; *** *** {displaystyle rho } = densidad; v{displaystyle v} = velocidad; w={displaystyle w=? δ δ 1{displaystyle delta ¿Qué? = longitud de la capa fronteriza transitoria; μ μ {displaystyle mu } = viscosidad; L{displaystyle L. = longitud característica.

Predicción de las condiciones de flujo convectivo en la capa límite de un cilindro mediante análisis dimensional

Mediante el uso de las ecuaciones de fuerza convectivas y viscosas en la capa de límites para un flujo cilíndrico puede predecir las condiciones de flujo convectivas en la capa de límite encontrando el número de Reynolds sin dimensión (Re{displaystyle Re.).

Fuerza preventiva: *** *** v2L{displaystyle rho v^{2} over L}

Fuerza viscosa: μ μ vδ δ 22{displaystyle {mu v over delta ¿Qué?

Haciéndolos iguales entre sí da:

*** *** v2L=μ μ vδ δ 22{displaystyle {rho v^{2} over L}={mu v over delta ¿Qué?

Resolviendo para delta da:

δ δ 2=μ μ L*** *** v{displaystyle delta ¿Qué? L over rho v}}

En forma adimensional:

Lδ δ 2=*** *** vLμ μ =Re{displaystyle {L over delta {fnK}={sqrt {rho vL over mu - Sí.

Donde Re{displaystyle Re. = Número de Reynolds; *** *** {displaystyle rho } = densidad; v{displaystyle v} = velocidad; δ δ 2{displaystyle delta _{2} = longitud de la capa fronteriza convectiva; μ μ {displaystyle mu } = viscosidad; L{displaystyle L. = longitud característica.

Ingesta de capa límite

La ingestión de la capa límite promete un aumento en la eficiencia del combustible de la aeronave con un propulsor montado en la popa que ingiere la capa límite del fuselaje lento y reactiva la estela para reducir la resistencia y mejorar la eficiencia de la propulsión. Para operar en un flujo de aire distorsionado, el ventilador es más pesado y su eficiencia se reduce, y su integración es un desafío. Se utiliza en conceptos como el Aurora D8 o el Nova de la agencia de investigación francesa Onera, ahorrando un 5% en crucero al ingerir el 40% de la capa límite del fuselaje.

Airbus presentó el concepto Nautilius en el congreso ICAS en septiembre de 2018: Para ingerir toda la capa límite del fuselaje, mientras se minimiza la distorsión del flujo azimutal, el fuselaje se divide en dos ejes con ventiladores con relación de derivación de 13-18:1. Las eficiencias de propulsión son de hasta un 90 %, como los rotores abiertos que giran en sentido contrario con motores más pequeños, livianos, menos complejos y ruidosos. Podría reducir el consumo de combustible en más de un 10 % en comparación con un motor habitual con una relación de derivación de 15:1 debajo del ala.