Campo vectorial solenoide
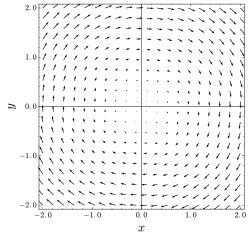
En cálculo vectorial, un campo vectorial solenoide (también conocido como campo vectorial incompresible, un campo vectorial sin divergencia o un campo transversal campo vectorial) es un campo vectorial v con divergencia cero en todos los puntos del campo:
Propiedades
El teorema de divergencia da una definición integral equivalente de un campo solenoidal; es decir, que para cualquier superficie cerrada, el flujo total neto a través de la superficie debe ser cero:
Donde dS{displaystyle dmathbf {S} es el exterior normal a cada elemento de superficie.
El teorema fundamental del cálculo vectorial establece que cualquier campo vectorial se puede expresar como la suma de un campo irrotacional y uno solenoidal. La condición de divergencia cero se cumple siempre que un campo vectorial v tiene solo un componente de potencial vectorial, porque la definición del potencial vectorial A es:
Etimología
Solenoide tiene su origen en la palabra griega para solenoide, que es σωληνοειδές (sōlēnoeidēs) que significa en forma de tubería, de σωλην (sōlēn) o tubería.
Ejemplos
- El campo magnético B (ver la ley de Gauss para el magnetismo)
- El campo de velocidad de un flujo de fluido incompresible
- El campo de vorticidad
- El campo eléctrico E en regiones neutrales*** *** e=0{displaystyle rho _{e}=0});
- La densidad actual J donde la densidad de carga es invariable, ∂ ∂ *** *** e∂ ∂ t=0{textstyle {frac {partial rho {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} t}=0}.
- El potencial vectorial magnético A en calibre Coulomb
Contenido relacionado
Julio (unidad)
Pascal (unidad)
Conjunto vacío








