Campo eléctrico

Un campo eléctrico (a veces campo E) es el campo físico que rodea partículas cargadas eléctricamente y ejerce fuerza sobre todas las demás partículas cargadas en el campo, ya sea atrayendo o repeliéndolos. También se refiere al campo físico de un sistema de partículas cargadas. Los campos eléctricos se originan a partir de cargas eléctricas y corrientes eléctricas variables en el tiempo. Los campos eléctricos y los campos magnéticos son manifestaciones del campo electromagnético, una de las cuatro interacciones fundamentales (también llamadas fuerzas) de la naturaleza.

Los campos eléctricos son importantes en muchas áreas de la física y se explotan en la tecnología eléctrica. En física y química atómica, por ejemplo, el campo eléctrico es la fuerza de atracción que mantiene unidos el núcleo atómico y los electrones en los átomos. También es la fuerza responsable del enlace químico entre átomos que dan como resultado moléculas.

El campo eléctrico se define como un campo vectorial que asocia a cada punto del espacio la fuerza electrostática (Coulombio) por unidad de carga ejercida sobre una carga de prueba positiva infinitesimal en reposo en ese punto. La unidad derivada del SI para el campo eléctrico es el voltio por metro (V/m), que es igual al newton por coulomb (N/C).

Descripción

Campo eléctrico de un punto positivo carga eléctrica suspendida sobre una hoja infinita de material conductor. El campo está representado por líneas de campo eléctrico, líneas que siguen la dirección del campo eléctrico en el espacio.

El campo eléctrico se define en cada punto del espacio como la fuerza por unidad de carga que experimentaría una carga de prueba positiva mínimamente pequeña si se mantuviera estacionaria en ese punto. Como el campo eléctrico se define en términos de fuerza, y la fuerza es un vector (es decir, tiene tanto magnitud como dirección), se deduce que un campo eléctrico es un campo vectorial. Los campos que se pueden definir de esta manera a veces se denominan campos de fuerza. El campo eléctrico actúa entre dos cargas de manera similar a como actúa el campo gravitatorio entre dos masas, ya que ambas obedecen una ley del inverso del cuadrado con la distancia. Esta es la base de la ley de Coulomb, que establece que, para cargas estacionarias, el campo eléctrico varía con la fuente de carga y varía inversamente con el cuadrado de la distancia desde la fuente. Esto significa que si la carga de la fuente se duplicara, el campo eléctrico se duplicaría, y si te alejas el doble de la fuente, el campo en ese punto sería solo una cuarta parte de su fuerza original.

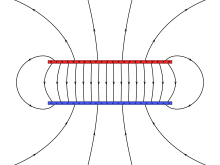
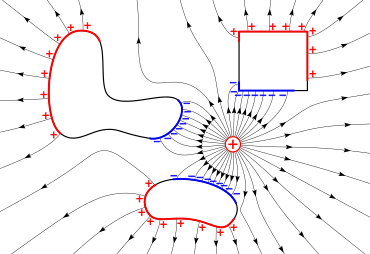
El campo eléctrico se puede visualizar con un conjunto de líneas cuya dirección en cada punto es la misma que la del campo, un concepto introducido por Michael Faraday, cuyo término 'líneas de fuerza' todavía se usa a veces. Esta ilustración tiene la propiedad útil de que la intensidad del campo es proporcional a la densidad de las líneas. Las líneas de campo debidas a cargas estacionarias tienen varias propiedades importantes, entre ellas, que siempre se originan en cargas positivas y terminan en cargas negativas, ingresan a todos los buenos conductores en ángulo recto y nunca se cruzan ni se cierran sobre sí mismas. Las líneas de campo son un concepto representativo; el campo en realidad impregna todo el espacio intermedio entre las líneas. Se pueden dibujar más o menos líneas dependiendo de la precisión con la que se desee representar el campo. El estudio de los campos eléctricos creados por cargas estacionarias se llama electrostática.

La ley de Faraday describe la relación entre un campo magnético variable en el tiempo y el campo eléctrico. Una forma de enunciar la ley de Faraday es que la curvatura del campo eléctrico es igual a la derivada temporal negativa del campo magnético. En ausencia de un campo magnético que varíe con el tiempo, el campo eléctrico se denomina conservativo (es decir, sin rotaciones). Esto implica que hay dos tipos de campos eléctricos: campos electrostáticos y campos que surgen de campos magnéticos variables en el tiempo. Si bien la naturaleza libre de ondulaciones del campo eléctrico estático permite un tratamiento más simple mediante la electrostática, los campos magnéticos variables en el tiempo generalmente se tratan como un componente de un campo electromagnético unificado. El estudio de los campos magnéticos y eléctricos variables en el tiempo se denomina electrodinámica.

Formulación matemática

Los campos eléctricos son causados por cargas eléctricas, descritas por la ley de Gauss, y campos magnéticos variables en el tiempo, descritos por la ley de inducción de Faraday. Juntas, estas leyes son suficientes para definir el comportamiento del campo eléctrico. Sin embargo, dado que el campo magnético se describe como una función del campo eléctrico, las ecuaciones de ambos campos están acopladas y juntas forman las ecuaciones de Maxwell que describen ambos campos como una función de cargas y corrientes.

Evidencia de un campo eléctrico: cacahuetes de estirofoam aferrados a la piel de un gato debido a la electricidad estática. El efecto triboeléctrico causa una carga electrostática para acumularse en la piel debido a los movimientos del gato. El campo eléctrico de la carga causa polarización de las moléculas del estirofoam debido a la inducción electrostática, resultando en una pequeña atracción de las piezas de plástico ligero a la piel cargada. Este efecto es también la causa de la fijación estática en la ropa.

Electrostática

En el caso especial de un estado estable (cargas estacionarias y corrientes), el efecto inductivo Maxwell-Faraday desaparece. Las dos ecuaciones resultantes (la ley de Gauss) ${displaystyle nabla cdot mathbf {E} ={frac {rho }{varepsilon ♪♪$ y la ley de Faraday sin plazo de inducción ${displaystyle nabla times mathbf {E} =0}$), tomados juntos, son equivalentes a la ley de Coulomb, que establece que una partícula con carga eléctrica ${displaystyle q_{1}$ en posición ${displaystyle mathbf {x} ¿Qué?$ ejerce una fuerza sobre una partícula con carga ${displaystyle q_{0}$ en posición ${displaystyle mathbf {x} ¿Qué?$ de:

$${displaystyle mathbf {F} ={frac {1}{4pi} varepsilon ¿Qué? {q_{1}{0} {c} {cH00}-cH00} {cH00}}} {f}} {f} {fn}}}} {f} {fn9} {f}}}}} {f}}}}} {f}}} {fnH0}} {f}}} {f} {f}}}}} {f}}}}}}}}} {f}}}} {f} {f} {f} {f}}}}}}}}}}}}}} {f} {f}}}}}} {f}}}}}} {f}} {f}} {f}}}} {f}}}} {f}}}}}}f}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}} }_{1,0},}$$

${fnMicrosoft Sans Serif} }_{1,0}$

${displaystyle mathbf {x} ¿Qué?$

${displaystyle mathbf {x} ¿Qué?$

Note que ${displaystyle varepsilon ¿Qué?$, la autorización eléctrica de vacío, debe ser sustituida con ${displaystyle varepsilon }$, permiso, cuando los cargos están en medios no vacíos. Cuando los cargos ${displaystyle q_{0}$ y ${displaystyle q_{1}$ tienen el mismo signo de que esta fuerza es positiva, dirigida lejos de la otra carga, indicando que las partículas se repelen. Cuando los cargos tienen signos a diferencia de que la fuerza es negativa, indicando que las partículas atraen. Para que sea fácil calcular la fuerza Coulomb en cualquier cargo a la posición ${displaystyle mathbf {x} ¿Qué?$ esta expresión se puede dividir por ${displaystyle q_{0}$ dejar una expresión que sólo depende de la otra carga (la fuente cargo)

$${displaystyle mathbf {E} (mathbf {x} _{0}={frac {mathbf {F} {fnK} {fnMicroc} {1}{4pi varepsilon ¿Qué? {fnK} {f}} {fnMitbf {f}}} {f}} {f}} {f}}} {fn} {f}}} {f}} {f}}} {f}} {f}}}}} {f}}}} {f}f}}}}} { }_{1,0}$$

${displaystyle mathbf {x} ¿Qué?$

${displaystyle q_{1}$

${displaystyle mathbf {x} ¿Qué?$

${displaystyle mathbf {x} ¿Qué?$

${displaystyle mathbf {x} ¿Qué?$

La fuerza Coulomb a cargo de magnitud ${displaystyle q}$ en cualquier punto del espacio es igual al producto de la carga y el campo eléctrico en ese punto

$${displaystyle mathbf {F} =qmathbf {E}$$

Principio de superposición

Debido a la linealidad de las ecuaciones de Maxwell, los campos eléctricos satisfacen el principio de superposición, que establece que el campo eléctrico total, en un momento, debido a una colección de cargos es igual a la suma vectorial de los campos eléctricos en ese momento debido a los cargos individuales. Este principio es útil para calcular el campo creado por múltiples cargos de punto. Si hay cargos ${displaystyle q_{1},q_{2},dotsq_{n}$ están estacionarios en el espacio en puntos ${displaystyle mathbf {x} _{1},mathbf {x} _{2},dotsmathbf {x} _{n}}$, en ausencia de corrientes, el principio de superposición dice que el campo resultante es la suma de los campos generados por cada partícula como se describe en la ley de Coulomb:

$${displaystyle {begin{aligned}mathbf {fnMicrosoft Sans Serif} {fnMicrosoft} {f} {cHFF} {cHFF} {f}} {cH0} {cH00} {cH00} {cH00} {cH00} {cH00}} {cH00} {cH0} {cH0} {cH00}} {cH00} {cH00}}} {cH00}}}} {c}}} {cH00} {cH00} {cH00} {cH00}} {cH00}}}}}}}} {c}}}}} {cH00} {cH00} {cH00} {cH00}} {cH00}cH00}}} {cH00} {cH00} {cH00} {ccH00}}}}}}}}}}}}}}} }_{1}+{1 over 4pi varepsilon _{0}{q_{2} over (mathbf {x} _{2}-mathbf {x})}{2} {hat {mathbf {r} }_{2}+{1 over 4pi varepsilon _{0}{q_{3} over (mathbf {x} _{3}-mathbf {x})}{2}{hat {mathbf {r} }_{3}+cdots \[2pt] varepsilon - Sí. ################################################################################################################################################################################################################################################################ }_{k}end{aligned}}$$

${displaystyle mathbf {hat {fnK}}$

${displaystyle mathbf {x} _{k}$

${displaystyle mathbf {x}$

Distribuciones continuas de carga

El principio de superposición permite el cálculo del campo eléctrico debido a una distribución continua de carga ${displaystyle rho (mathbf {x})}$ (donde) ${displaystyle rho }$ es la densidad de carga en coulombs por metro cúbico). Al considerar el cargo ${displaystyle rho (mathbf {x}dV}$ en cada pequeño volumen del espacio ${displaystyle dV}$ punto ${displaystyle mathbf {x}$ como una carga de punto, el campo eléctrico resultante, ${displaystyle dmathbf {E}$, al punto ${displaystyle mathbf {x}$ puede calcularse

$${f} {f} {f}} {f}} {f}} {f}} {f}} {f}} {f}} {f}} {f}}} {f}} {f} {f}} {f}}} {f} {f}}} {f}}}} {f}}}} {f} {f}}} {f}}}} {f}}f}}}}} {f} {f} {f}}}}} {f} {f} {f}} {f}}}}}}}}}} {f}}}}}} {f}} {f}} {f}}}}}}}}}} {f}}}}}}}}}}} {f}}}} {f}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}$$

${displaystyle {hat {fnMithbf {}}}} {f}}} {f}}} {f}}}}$

${displaystyle mathbf {x}$

${displaystyle mathbf {x}$

${displaystyle V}$

$${displaystyle mathbf {E} (mathbf {x}={frac {1}{4pi varepsilon _{0}}}iiint _{V},{rho (mathbf {x} ')d V.$$

${displaystyle sigma (mathbf {x})}$

${displaystyle sigma }$

$${displaystyle mathbf {E} (mathbf {x}={frac {1}{4pi varepsilon _{0}}iint ¿Por qué? A over (mathbf {x} '-mathbf {x} {2}{hat {mathbf {r}}}}$$

${displaystyle lambda (mathbf {x})}$

${displaystyle lambda }$

$${displaystyle mathbf {E} (mathbf {x}={frac {1}{4pi varepsilon _{0}}}int _{P},{lambda (mathbf {x} ')d L over (mathbf {x} '-mathbf {x} {2}{hat {mathbf {r}}}}$$

Potencial eléctrico

Si un sistema es estático, de tal manera que los campos magnéticos no están variando tiempo, entonces por la ley de Faraday, el campo eléctrico es libre de rizos. En este caso, se puede definir un potencial eléctrico, es decir, una función ${displaystyle Phi }$ tales que ${displaystyle mathbf {E} =-nabla Phi }$. Esto es análogo al potencial gravitatorio. La diferencia entre el potencial eléctrico en dos puntos en el espacio se llama la diferencia potencial (o tensión) entre los dos puntos.

En general, sin embargo, el campo eléctrico no puede describirse independientemente del campo magnético. Dado el potencial vectorial magnético, A, definido de modo que ${displaystyle mathbf {B} =nabla times mathbf {A}$, uno todavía puede definir un potencial eléctrico ${displaystyle Phi }$ tal que:

$${displaystyle mathbf {E} =-nabla Phi -{frac {partial mathbf {A} {fn} {fnK}}} {fn}} {fn}} {fn}} {fn}}} {fn}}}}} {f}}}} {fn}}}}}} {f}}}}}}}}} {$$

${displaystyle nabla Phi }$

${displaystyle {frac {partial mathbf {A} {fn} {fnK}}} {fn}} {fn}} {fn}} {fn}}} {fn}}}}} {f}}}} {fn}}}}}} {f}}}}}}}}} {$

La ley de inducción de Faraday se puede recuperar tomando el rizo de esa ecuación

$${displaystyle nabla times mathbf {E} =-{frac {partial (nabla times mathbf {A})}{partial t}=-{frac {partial mathbf {B}{partial t}}$$

Representación de carga continua vs. discreta

Las ecuaciones del electromagnetismo se describen mejor en una descripción continua. Sin embargo, los cargos a veces se describen mejor como puntos discretos; por ejemplo, algunos modelos pueden describir los electrones como fuentes puntuales donde la densidad de carga es infinita en una sección infinitesimal del espacio.

Un cargo ${displaystyle q}$ situado en ${displaystyle mathbf {r} ¿Qué?$ se puede describir matemáticamente como una densidad de carga ${displaystyle rho (mathbf {r})=qdelta (mathbf {r} -mathbf {r} _{0})}$, donde se utiliza la función Dirac delta (en tres dimensiones). Por el contrario, una distribución de carga puede ser aproximada por muchos cargos de puntos pequeños.

Campos electrostáticos

Ilustración del campo eléctrico que rodea una carga positiva (rojo) y negativa (azul)

Los campos electrostáticos son campos eléctricos que no cambian con el tiempo. Dichos campos están presentes cuando los sistemas de materia cargada están estacionarios o cuando las corrientes eléctricas no cambian. En ese caso, la ley de Coulomb describe completamente el campo.

Paralelos entre campos electrostáticos y gravitacionales

La ley de Coulomb, que describe la interacción de las cargas eléctricas:

$${displaystyle mathbf {F} =qleft({frac {Q}{4pi varepsilon ¿Qué? Oh, Dios mío.$$

$${displaystyle mathbf {F} =mleft(-GM{frac {mathbf {hat {r} } {fnMitbf {r} {fn}}derecha)=mmathbf {g}$$

${textstyle mathbf {hat {r} # Mathbf {frac {r} {fnh00}$

Esto sugiere similitudes entre el campo eléctrico E y el campo gravitacional g, o sus potenciales asociados. A la masa a veces se le llama "carga gravitacional".

Las fuerzas electrostática y gravitacional son centrales, conservativas y obedecen a la ley del inverso del cuadrado.

Campos uniformes

Ilustración del campo eléctrico entre dos placas conductivas paralelas de tamaño finito (conocido como condensador de placa paralela). En medio de las placas, lejos de cualquier borde, el campo eléctrico es muy uniforme.

Un campo uniforme es aquel en el que el campo eléctrico es constante en todos los puntos. Se puede aproximar colocando dos placas conductoras paralelas entre sí y manteniendo un voltaje (diferencia de potencial) entre ellas; es solo una aproximación debido a los efectos de contorno (cerca del borde de los planos, el campo eléctrico se distorsiona porque el plano no continúa). Suponiendo planos infinitos, la magnitud del campo eléctrico E es:

$${displaystyle E=-{frac {Delta V}{d}}}$$

Campos electrodinámicos

El campo eléctrico (líneas con flechas) de un cargo (+) induce cargas superficiales ()rojo y azul áreas) en objetos metálicos debido a la inducción electrostática.

Los campos electrodinámicos son campos eléctricos que cambian con el tiempo, por ejemplo cuando los cargos están en movimiento. En este caso, se produce un campo magnético de acuerdo con la ley de Ampère (con la adición de Maxwell), que, junto con otras ecuaciones de Maxwell, define el campo magnético, ${displaystyle mathbf {B}$, en términos de su rizo:

$${displaystyle nabla times mathbf {B} =mu _{0}left(mathbf) {J} +varepsilon ¿Por qué?$$

${displaystyle mathbf {J}$

${displaystyle mu _{0}}$

${displaystyle varepsilon ¿Qué?$

Es decir, tanto las corrientes eléctricas (es decir, cargas en movimiento uniforme) como la derivada temporal (parcial) del campo eléctrico contribuyen directamente al campo magnético. Además, la ecuación de Maxwell-Faraday establece

$${displaystyle nabla times mathbf {E} =-{frac {partial mathbf {B} {fnMicrosoft Sans Serif}$$

$${displaystyle mathbf {F} =qmathbf {E} +qmathbf {v} times mathbf {B}$$

Energía en el campo eléctrico

La energía total por unidad de volumen almacenada por el campo electromagnético es

$${displaystyle u_{text{EM}={frac {varepsilon }{2} {E} Silencio. {1}{2mu - Hola.$$

${displaystyle mu }$

Como los campos E y B están acoplados, Sería engañoso dividir esta expresión en "eléctrico" y "magnético" contribuciones. En particular, un campo electrostático en cualquier marco de referencia dado en general se transforma en un campo con un componente magnético en un marco en movimiento relativo. En consecuencia, descomponer el campo electromagnético en un componente eléctrico y magnético es específico del marco, y de manera similar para la energía asociada.

La energía total U_EM almacenada en el campo electromagnético en un volumen dado V es

$${displaystyle U_{text{EM}={2}int ¿Qué? Silencio. {1}{mu} - Hola.$$

El campo de desplazamiento eléctrico

Ecuación definitiva de campos vectoriales

En presencia de materia, es útil extender la noción de campo eléctrico a tres campos vectoriales:

$${displaystyle mathbf {D} = 'varepsilon ♪♪Mathbf {E} +mathbf {P}$$

Relación constitutiva

Los campos E y D están relacionados por la permitividad del material, ε.

Para materiales lineales, homogéneos e isotrópicos, E y D son proporcionales y constantes en toda la región, no hay dependencia de la posición:

$${displaystyle mathbf {D} (mathbf {r})=varepsilon mathbf {E} (mathbf {r})}$$

Para materiales no homogéneos, existe una dependencia de posición en todo el material:

$${displaystyle mathbf {D} (mathbf {r})=varepsilon (mathbf {r})mathbf {E} (mathbf {r})}$$

Para materiales anisotrópicos, los campos E y D son no son paralelos, por lo que E y D están relacionados por el tensor de permitividad (un campo tensor de segundo orden), en forma de componentes:

$${displaystyle D_{i}=varepsilon ¿Qué?$$

Para medios no lineales, E y D no son proporcionales. Los materiales pueden tener diferentes grados de linealidad, homogeneidad e isotropía.

Efectos relativistas sobre el campo eléctrico

Carga puntual en movimiento uniforme

La invariancia de la forma de las ecuaciones de Maxwell bajo la transformación de Lorentz se puede utilizar para derivar el campo eléctrico de una carga puntual en movimiento uniforme. La carga de una partícula se considera marco invariante, como lo respalda la evidencia experimental. Alternativamente, el campo eléctrico de cargas puntuales que se mueven uniformemente se puede derivar de la transformación de Lorentz de cuatro fuerzas experimentada por cargas de prueba en el marco de reposo de la fuente dada por la ley de Coulomb y asignando campo eléctrico y campo magnético por su definición dada por la forma de la fuerza de Lorentz. Sin embargo, la siguiente ecuación solo es aplicable cuando no hay aceleración involucrada en la historia de la partícula donde se puede considerar la ley de Coulomb o se pueden usar argumentos de simetría para resolver las ecuaciones de Maxwell de una manera simple. Por lo tanto, el campo eléctrico de una carga puntual que se mueve uniformemente viene dado por:

$${displaystyle mathbf {E} ={frac {q}{4piepsilon ¿Qué? mathbf {r}$$

${displaystyle q}$

${displaystyle mathbf {r}$

${displaystyle beta }$

${displaystyle theta }$

${displaystyle mathbf {r}$

La ecuación anterior se reduce a la dada por la ley de Coulomb para velocidades no relativistas de la carga puntual. La simetría esférica no se satisface debido a la ruptura de la simetría en el problema mediante la especificación de la dirección de la velocidad para el cálculo del campo. Para ilustrar esto, las líneas de campo de cargas en movimiento a veces se representan como líneas radiales desigualmente espaciadas que aparecerían igualmente espaciadas en un marco de referencia de movimiento conjunto.

Propagación de perturbaciones en campos eléctricos

La teoría especial de la relatividad impone el principio de localidad, que requiere que la causa y el efecto sean eventos separados en el tiempo donde la eficacia causal no viaja más rápido que la velocidad de la luz. Se encuentra que las leyes de Maxwell confirman este punto de vista, ya que las soluciones generales de los campos se dan en términos de tiempo retardado, lo que indica que las perturbaciones electromagnéticas viajan a la velocidad de la luz. El tiempo avanzado, que también proporciona una solución para la ley de Maxwell, se ignora como una solución no física.

Un ejemplo ilustrativo que muestra la radiación bremsstrahlung: Líneas de campo y módulo del campo eléctrico generado por una carga (negativa) se mueven primero a una velocidad constante y luego se detienen rápidamente para mostrar la onda electromagnética generada y propagación de perturbaciones en el campo electromagnético.

Para el movimiento de una partícula cargada, considerando por ejemplo el caso de una partícula en movimiento con el campo eléctrico descrito arriba llegando a una parada abrupta, los campos eléctricos en los puntos alejados de ella no vuelven inmediatamente al dado clásicamente para una carga estacionaria. Al detenerse, el campo alrededor de los puntos estacionarios comienza a volver al estado esperado y este efecto se propaga hacia el exterior a la velocidad de la luz, mientras que las líneas de campo eléctrico más alejadas continuarán apuntando radialmente hacia una supuesta carga en movimiento. Esta partícula virtual nunca estará fuera del rango de propagación de la perturbación en el campo electromagnético, ya que las partículas cargadas están restringidas para tener velocidades más lentas que la de la luz, lo que hace imposible construir una superficie gaussiana en esta región que viole Gauss' ley. Otra dificultad técnica que respalda esto es que las partículas cargadas que viajan más rápido que o igual a la velocidad de la luz ya no tienen un tiempo de retardo único. Dado que las líneas de campo eléctrico son continuas, se genera un pulso electromagnético de radiación que se conecta en el límite de esta perturbación y viaja hacia el exterior a la velocidad de la luz. En general, cualquier carga puntual que se acelera irradia ondas electromagnéticas; sin embargo, es posible que no se produzca una aceleración en un sistema de cargas.

Carga puntual que se mueve arbitrariamente

Para cargas puntuales que se mueven arbitrariamente, la propagación de campos potenciales como los campos de calibre de Lorenz a la velocidad de la luz debe tenerse en cuenta mediante el uso del potencial de Liénard-Wiechert. Dado que los potenciales satisfacen las ecuaciones de Maxwell, los campos derivados de la carga puntual también satisfacen las ecuaciones de Maxwell. El campo eléctrico se expresa como:

$${displaystyle mathbf {E} (mathbf {r}mathbf {t}={frac {1}{4pi varepsilon _{0}}}left({frac {q(mathbf { n} {} {}} {}}}}} {m}}}m} {m}} {m} {m}}}}}}}}m} {m} {m}m}m} {m}m} {m}m} {m}m}m}m} {m}m}}m} {m}m} {m}m}m}m}m}m}m} {m}m} {m}m}m}m} {f}}fn}m}s0}m} {f}m} {m}f}}m}}} ¿Qué? ¿Por qué? - Hola. - Mathbf. - ¿Qué? {qmathbf {n} - ¿Por qué? ¿Qué? {beta}_ {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fn}} {bign}} {c(1-mathbf {n} ¿Por qué? - Hola. - Mathbf. ¿Qué?$$

${displaystyle q}$

${textstyle {}}$

${textstyle {r}_{s}(t)}$

${fnK} {fn} {fnh00}}$

${fnMicrosoft {fnMicrosoft} - Sí.$

${textstyle gamma (t)}$

${displaystyle ¿Qué? - Mathbf {r} - Hola.$

La singularidad de la solución ${textstyle {}}$ para dar ${displaystyle mathbf {t}$, ${displaystyle mathbf {r}$ y ${displaystyle r_{s}(t)}$ es válido para partículas cargadas que se mueven más lento que la velocidad de la luz. Se sabe que la radiación electromagnética de las cargas de aceleración es causada por el término dependiente de aceleración en el campo eléctrico del cual se obtiene corrección relativista para la fórmula Larmor.

Hay otro conjunto de soluciones para la ecuación de Maxwell de la misma forma pero para el tiempo avanzado ${textstyle {}$ en lugar de retraso dado como solución de:

${displaystyle ################################################################################################################################################################################################################################################################ - Mathbf {r} ¿Qué?$

Dado que la interpretación física de esto indica que el campo eléctrico en un punto está gobernado por el estado de la partícula en un momento futuro, se considera una solución no física y, por lo tanto, se desprecia. Sin embargo, ha habido teorías que exploran las soluciones temporales avanzadas de las ecuaciones de Maxwell, como la teoría absorbente de Feynman Wheeler.

La ecuación anterior, aunque es coherente con la de las cargas puntuales que se mueven uniformemente, así como con su límite no relativista, no está corregida por los efectos de la mecánica cuántica.

Algunos valores comunes de campo eléctrico

• Cable infinito con densidad de carga uniforme ${displaystyle lambda }$ tiene campo eléctrico a distancia ${displaystyle x}$ de ella como ${displaystyle {frac {2Klambda } {x} {hat {x}} {fn} {fn}} {fn}} {fn}} {fn}}} {fn}}} {fn}} {fn}}}} {fn}}} {f}}} {f}}}}} {f}}}}} {f}}}} {f}}}}}}} {f}}} {f}} {f}}}}} {f}}}} {f}}}} {f}}}}} {f}}} {f}}}}}}}}} {f}}}}}} {f}} {f} {f} {f}}} {f}}}} {f}}}}}}} {f}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$
• Superficie infinitamente grande con densidad de carga ${displaystyle sigma }$ tiene campo eléctrico a distancia ${displaystyle x}$ de ella como ${displaystyle {frac {sigma }{2epsilon {fnK} {fnK}} {fnK}} {fnK}}}} {fn}} {fn}}} {fn}} {fn}}}}} {fn}}} {fn}}}}}}} {f}}}}} {fnf}}}}}}} {f}}} {f}}}}}}}}}}}} {f}}}}}}}}}}}}}}} {f}}}}} {f}}}} {f}}}}}}}}}}}}}}}} {f}}}}}} {f}}}} {f}}}}}}} {f}}}}} {f}}} {f}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$
• Cilindro infinitamente largo con densidad de carga uniforme ${displaystyle lambda }$ que se carga a lo largo de la unidad del cilindro tiene campo eléctrico a una distancia ${displaystyle x}$ de ella como ${displaystyle {frac {2Klambda } {x} {hat {x}} {fn} {fn}} {fn}} {fn}} {fn}}} {fn}}} {fn}} {fn}}}} {fn}}} {f}}} {f}}}}} {f}}}}} {f}}}} {f}}}}}}} {f}}} {f}} {f}}}}} {f}}}} {f}}}} {f}}}}} {f}}} {f}}}}}}}}} {f}}}}}} {f}} {f} {f} {f}}} {f}}}} {f}}}}}}} {f}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$ mientras que ${displaystyle 0}$ por todas partes dentro del cilindro
• Esfera de radio de carga uniforme ${displaystyle R.$, densidad de carga de volumen ${displaystyle rho }$ y cargo total ${displaystyle Q}$ tiene campo eléctrico a distancia ${displaystyle x}$ de ella como ${displaystyle {frac {KQ}{x}}{hat {x}} {f}} {f}} {f}} {f}}}}} {f}}}} {f}}}}}} {f}}}}$ mientras el campo eléctrico en un punto ${displaystyle {vec}}$ interior esfera desde su centro es dada por ${displaystyle {frac {fnK} {fnK}} {fn}} {fn}} {fn}}} {fn}}}} {fn}}}} {fn}}}}}}}} {f}}}}} {f}}}}} {f}}}}}}}}}}}}$
• Esfera de radio de carga uniforme ${displaystyle R.$, densidad de carga superficial ${displaystyle sigma }$ y cargo total ${displaystyle Q}$ tiene campo eléctrico a distancia ${displaystyle x}$ de ella como ${displaystyle {frac {KQ}{x}}{hat {x}} {f}} {f}} {f}} {f}}}}} {f}}}} {f}}}}}} {f}}}}$ mientras que el campo eléctrico dentro es ${displaystyle 0}$
• Campo eléctrico infinitamente cerca de una superficie conductora en equilibrio electrostático con densidad de carga ${displaystyle sigma }$ en ese punto ${displaystyle {frac {sigma }{epsilon {fnK} {fnK}} {fnK}} {fnK}}}} {fn}} {fn}}} {fn}} {fn}}}}} {fn}}} {fn}}}}}}} {f}}}}} {fnf}}}}}}} {f}}} {f}}}}}}}}}}}} {f}}}}}}}}}}}}}}} {f}}}}} {f}}}} {f}}}}}}}}}}}}}}}} {f}}}}}} {f}}}} {f}}}}}}} {f}}}}} {f}}} {f}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$
• Anillo de carga uniforme con cargo total ${displaystyle Q}$ tiene campo eléctrico a distancia ${displaystyle x}$ a lo largo de su eje ${displaystyle {frac {KQx}{2}+x^{2}}{3/2}}{hat {x}}}}}} {f}}} {f}}}} {f}}}} {f}}}}} {f}}}} {f}}}$'
• Disco de radio de carga uniforme ${displaystyle R.$ y densidad de carga ${displaystyle sigma }$ tiene campo eléctrico a distancia ${displaystyle x}$ a lo largo de su eje ${displaystyle {frac {sigma }{2epsilon ¿Qué? {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}$
• Campo eléctrico debido a la dipole del momento de la dipole ${displaystyle {vec}}$ a distancia ${displaystyle x}$ desde su centro a lo largo del plano ecuatorial se da como ${displaystyle - ¿Qué? {}} {x^{3}}} {}}}} {c}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}}}}} {c}}}}}}} {c}}}}} {c}}}}}}}}} {c}}}}}}}} {}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {$ y lo mismo a lo largo de la línea axial se aproxima a ${fnMicroc {fnMicroc} {}} {x^{3}}} {}}}} {c}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}}}}} {c}}}}}}} {c}}} {}}}}}}}}}} {c}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {$ para ${displaystyle x}$ mucho más grande que la distancia entre dipoles. La mayor generalización es dada por la expansión multipole.