Camino euleriano

En teoría de grafos, un camino euleriano (o camino euleriano) es un sendero en un grafo finito que visita cada borde exactamente una vez (lo que permite volver a visitar los vértices). De manera similar, un circuito euleriano o ciclo euleriano es un sendero euleriano que comienza y termina en el mismo vértice. Fueron discutidos por primera vez por Leonhard Euler mientras resolvía el famoso problema de los Siete Puentes de Königsberg en 1736. El problema se puede plantear matemáticamente así:

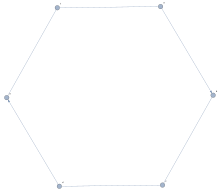
Dado el gráfico en la imagen, ¿es posible construir un camino (o un ciclo; es decir, un camino que comienza y termina en el mismo vértice) que visita cada borde exactamente una vez?

Euler demostró que una condición necesaria para la existencia de circuitos eulerianos es que todos los vértices del grafo tengan un grado par, y afirmó sin pruebas que los grafos conectados con todos los vértices de grado par tienen un circuito euleriano. La primera prueba completa de esta última afirmación fue publicada póstumamente en 1873 por Carl Hierholzer. Esto se conoce como Teorema de Euler:

Un gráfico conectado tiene un ciclo Euler si y sólo si cada vértice tiene grado.

El término gráfico euleriano tiene dos significados comunes en la teoría de grafos. Un significado es un gráfico con un circuito euleriano y el otro es un gráfico con cada vértice de grado par. Estas definiciones coinciden para gráficos conectados.

Para la existencia de senderos eulerianos es necesario que cero o dos vértices tengan grado impar; esto significa que el gráfico de Königsberg no es euleriano. Si no hay vértices de grado impar, todos los caminos eulerianos son circuitos. Si hay exactamente dos vértices de grado impar, todos los senderos eulerianos comienzan en uno de ellos y terminan en el otro. Un grafo que tiene un camino euleriano pero no un circuito euleriano se llama semi-Euleriano.

Definición

Un sendero euleriano, o camino de Euler, en un gráfico no dirigido es un recorrido que utiliza cada borde exactamente una vez. Si tal recorrido existe, el gráfico se llama transitable o semi-eulerian.

Un ciclo euleriano, también llamado circuito euleriano o giro de Euler, en un grafo no dirigido es un ciclo que utiliza cada arista exactamente una vez.. Si tal ciclo existe, el gráfico se llama Eulerian o unicursal. El término "gráfico euleriano" A veces también se usa en un sentido más débil para denotar un gráfico donde cada vértice tiene un grado par. Para gráficos finitos conectados, las dos definiciones son equivalentes, mientras que un gráfico posiblemente no conectado es euleriano en el sentido más débil si y sólo si cada componente conectado tiene un ciclo euleriano.

Did you mean:

For directed graphs, "path" has to be replaced with directed path and n#34;cycle" with directed cycle.

La definición y las propiedades de los senderos, ciclos y gráficos eulerianos también son válidas para multigrafos.

Una orientación euleriana de un grafo no dirigido G es una asignación de una dirección a cada arista de G tal que, en cada vértice v, el grado de entrada de v es igual al grado de salida de v. Tal orientación existe para cualquier gráfico no dirigido en el que cada vértice tenga un grado par, y se puede encontrar construyendo un recorrido de Euler en cada componente conectado de G y luego orientando los bordes de acuerdo con el recorrido. Cada orientación euleriana de un grafo conexo es una orientación fuerte, una orientación que hace que el grafo dirigido resultante sea fuertemente conexo.

Propiedades

• Un gráfico no dirigido tiene un ciclo eurístico si y sólo si cada vértice tiene grado, y todos sus vértices con grado no cero pertenecen a un único componente conectado.
• Un gráfico no dirigido se puede descomponer en ciclos de disyunción de bordes si y sólo si todos sus vértices tienen incluso grado. Por lo tanto, un gráfico tiene un ciclo Eulerian si y sólo si se puede descomponer en ciclos de disjoint de bordes y sus vértices no de grado pertenecen a un único componente conectado.
• Un gráfico no redirigido tiene un sendero Eulerian si y sólo si exactamente cero o dos vértices tienen un grado extraño, y todos sus vértices con un grado no cero pertenecen a un solo componente conectado
• Un gráfico dirigido tiene un ciclo eurístico si y sólo si cada vértice tiene igual en grado y grado, y todos sus vértices con grado no cero pertenecen a un solo componente fuertemente conectado. Equivalentemente, un gráfico dirigido tiene un ciclo eulerio si y sólo si se puede descomponer en ciclos dirigidos de disjoint de borde y todos sus vértices con grado no cero pertenecen a un solo componente fuertemente conectado.
• Un gráfico dirigido tiene una ruta euleria si y sólo si en la mayoría de un vértice tiene (sin derecho) = 1, en la mayoría de un vértice tiene (en grados) = 1, cada otro vértice tiene igual en grado y fuera de acuerdo, y todos sus vértices con grado no cero pertenecen a un solo componente conectado del gráfico no dirigido subyacente.

Construcción de senderos y circuitos eulerianos

Did you mean:

Fleury 's algorithm

El

algoritmo de Fleury es un algoritmo elegante pero ineficiente que data de 1883. Considere un gráfico que se sabe que tiene todas las aristas en el mismo componente y como máximo dos vértices de grado impar. El algoritmo comienza en un vértice de grado impar o, si el gráfico no tiene ninguno, comienza con un vértice elegido arbitrariamente. En cada paso, elige el siguiente borde en la ruta para que sea uno cuya eliminación no desconectaría el gráfico, a menos que no exista tal borde, en cuyo caso elige el borde restante que queda en el vértice actual. Luego se mueve al otro punto final de ese borde y lo elimina. Al final del algoritmo no quedan aristas, y la secuencia de la que se eligieron las aristas forma un ciclo euleriano si el gráfico no tiene vértices de grado impar, o un sendero euleriano si hay exactamente dos vértices de grado impar.

Mientras que Gráfico traversal en el algoritmo de Fleury es lineal en el número de bordes, es decir. O()SilencioESilencio){displaystyle O(viviendas)}, también necesitamos tener en cuenta la complejidad de detectar puentes. Si vamos a reequilibrar el algoritmo lineal de Tarjan después de la eliminación de cada borde, el algoritmo de Fleury tendrá una complejidad de tiempo O()SilencioESilencio2){displaystyle O {}. Un algoritmo dinámico de búsqueda de puentes de Thorup (2000) permite mejorarlo O()SilencioESilencio⋅ ⋅ log3⁡ ⁡ SilencioESilencio⋅ ⋅ log⁡ ⁡ log⁡ ⁡ SilencioESilencio){displaystyle O(Principe a la muertecdot log ^{3}Sobrevivircdot logloglog ANTERIOR, pero esto sigue siendo significativamente más lento que algoritmos alternativos.

Did you mean:

Hierholzer 's algorithm

Did you mean:

Hierholzer 's 1873 paper provides a different method for finding Euler cycles that is more efficient than Fleury 's algorithm:

• Elija cualquier vértice inicial v, y seguir un rastro de bordes de ese vértice hasta volver a v. No es posible quedar atrapado en cualquier vértice que no sea v, porque el grado de todos los vértices asegura que, cuando el sendero entra en otro vértice w debe haber un borde que no se usa w. El recorrido formado de esta manera es un recorrido cerrado, pero no puede cubrir todos los vértices y bordes del gráfico inicial.
• Mientras exista un vértice u que pertenece a la gira actual pero que tiene bordes adyacentes no parte de la gira, iniciar otro sendero desde u, siguiendo bordes no utilizados hasta volver a u, y unirse a la gira formada de esta manera a la gira anterior.
• Dado que suponemos que el gráfico original está conectado, repetir el paso anterior agotará todos los bordes del gráfico.

Mediante el uso de una estructura de datos como una lista doblemente vinculada para mantener el conjunto de bordes no utilizados incidente a cada vértice, para mantener la lista de vértices en el recorrido actual que tienen bordes no utilizados, y para mantener el tour en sí mismo, las operaciones individuales del algoritmo (descubriendo bordes no utilizados saliendo de cada vértice, encontrando un nuevo vértice inicial para un tour, y conectando dos tours que comparten un vértice) cada vez lineal O()SilencioESilencio){displaystyle O(viviendas)}.

Este algoritmo también puede ser implementado con una deque. Debido a que sólo es posible quedarse atascado cuando el deque representa un recorrido cerrado, uno debe girar el deque al quitar los bordes de la cola y añadirlos a la cabeza hasta que se descomponen, y luego continuar hasta que todos los bordes sean contados. Esto también toma tiempo lineal, ya que el número de rotaciones realizadas nunca es mayor que SilencioESilencio{displaystyle Silencioso (intuitivamente, cualquier borde "malo" se mueve a la cabeza, mientras que los bordes frescos se añaden a la cola)

Contando circuitos eulerianos

Problemas de complejidad

El número de circuitos eulerianos en dígrafos se puede calcular utilizando el llamado teorema BEST, que lleva el nombre de De Bruijn, van Aardenne-Ehrenfest, Smith y Tutte. La fórmula establece que el número de circuitos eulerianos en un dígrafo es el producto de ciertos factoriales de grado y el número de arborescencias enraizadas. Este último se puede calcular como un determinante, mediante el teorema del árbol matricial, dando un algoritmo de tiempo polinomial.

El teorema BEST se expresa por primera vez en esta forma en una "nota agregada en la prueba" al artículo de Aardenne-Ehrenfest y de Bruijn (1951). La prueba original era biyectiva y generalizaba las secuencias de De Bruijn. Es una variación de un resultado anterior de Smith y Tutte (1941).

Contar el número de circuitos eulerianos en gráficos no dirigidos es mucho más difícil. Se sabe que este problema es #P-completo. En una dirección positiva, se cree que un enfoque de Monte Carlo de cadena de Markov, a través de las transformaciones de Kotzig (introducidas por Anton Kotzig en 1968) proporciona una aproximación clara para el número de circuitos eulerianos en un gráfico, aunque como sin embargo, no hay prueba de este hecho (incluso para gráficas de grado acotado).

Casos especiales

McKay y Robinson (1995) determinaron una fórmula asintótica para el número de circuitos eulerianos en los gráficos completos:

ec⁡ ⁡ ()Kn)=2()n+1)2π π 12e− − n22+1112n()n− − 2)()n+1)2()1+O()n− − 12+ε ε )).{displaystyle operatorname {ec}=2^{frac {(n+1)}}pi ^{frac {1}{2}}e^{frac} {frac} {frac}} {fnf}} {f}} {fnf}} {fnfnf}f}}fnf}}}f}}}}}}}f}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fnf}fnf}}fnf}fnfnf}f}f}fnfnfnfnfnfnfnfnfnfn}}}}}}}} {-n^{2}{2}}{2} {bigl {11}}n^{frac {(n-2)}{2}}{bigl (}1+O(n^{-{-frac {1}{2}+epsilon }){bigr)}}}}

Más tarde, M.I. Isaev (2009) para gráficos bipartitos completos:

ec⁡ ⁡ ()Kn,n)=()n2− − 1)!2n2n2− − n+12π π − − n+12nn− − 1()1+O()n− − 12+ε ε )).{displaystyle operatorname {ec} (K_{n,n})=left({frac} ¡No! {1} {2}}pi ^{-n+{frac} {1}{2}}n^{n-1}{bigl (}1+O(n^{-{frac {1}{2}}+epsilon }){bigr)}} {bigr]}

Aplicaciones

Los rastros eulerianos se utilizan en bioinformática para reconstruir la secuencia de ADN a partir de sus fragmentos. También se utilizan en el diseño de circuitos CMOS para encontrar el orden óptimo de las puertas lógicas. Existen algunos algoritmos para procesar árboles que se basan en un recorrido de Euler por el árbol (donde cada borde se trata como un par de arcos). Las secuencias de De Bruijn se pueden construir como senderos eulerianos de gráficos de De Bruijn.

En gráficos infinitos

En un gráfico infinito, el concepto correspondiente a un sendero euleriano o ciclo euleriano es una línea euleriana, un sendero doblemente infinito que cubre todos los bordes del gráfico. No es suficiente para la existencia de tal sendero que el grafo esté conexo y que todos los grados de los vértices sean pares; por ejemplo, el gráfico infinito de Cayley que se muestra, con todos los grados de vértice iguales a cuatro, no tiene línea euleriana. Las gráficas infinitas que contienen líneas eulerianas fueron caracterizadas por Erdõs, Grünwald & Weiszfeld (1936). Para que un grafo o multigrafo infinito G tenga una recta euleriana, es necesario y suficiente que se cumplan todas las condiciones siguientes:

• G está conectado.
• G tiene conjuntos contables de vértices y bordes.
• G no tiene vértices de (finito) grado extraño.
• Eliminación de cualquier subgrafo finito S desde G hojas en la mayoría de dos componentes conectados infinitos en el gráfico restante, y si S tiene incluso grado en cada uno de sus vértices y luego la eliminación S deja exactamente un componente conectado infinito.

Gráficos eulerianos no dirigidos

Euler estableció una condición necesaria para que un grafo finito sea euleriano, ya que todos los vértices deben tener grados pares. Hierholzer demostró que esta es una condición suficiente en un artículo publicado en 1873. Esto lleva a la siguiente afirmación necesaria y suficiente sobre lo que debe tener un grafo finito para ser euleriano: Un grafo finito conexo no dirigido es euleriano si y sólo si cada vértice de G tiene incluso grado.

Veblen demostró el siguiente resultado en 1912: Un grafo conexo no dirigido es euleriano si y sólo si es la unión disjunta de algunos ciclos.

Hierholzer desarrolló un algoritmo de tiempo lineal para construir un recorrido euleriano en un gráfico no dirigido.

Gráficos eulerianos dirigidos

Es posible tener un gráfico dirigido que tenga todos los grados pares pero que no sea euleriano. Dado que un circuito euleriano sale de un vértice el mismo número de veces que entra en ese vértice, una condición necesaria para que exista un circuito euleriano es que los grados de entrada y salida sean iguales en cada vértice. Evidentemente, la conectividad también es necesaria. König demostró que estas condiciones también son suficientes. Es decir, un grafo dirigido es euleriano si y sólo si está conexo y los grados de entrada y salida son iguales en cada vértice.

Did you mean:

In this theorem it doesn't matter whether "connected#34; means "weakly connected#34; or "strongly connected" since they are equivalent for Eulerian graphs.

Did you mean:

Hierholzer 's linear time algorithm for constructing an Eulerian tour is also applicable to directed graphs.

Gráficos eulerianos mixtos

Si un gráfico mixto solo tiene grados pares, no se garantiza que sea un gráfico euleriano. Esto significa que la uniformidad es una condición necesaria pero no suficiente para que una gráfica mixta sea euleriana. Si un gráfico mixto es par y simétrico, se garantiza que será simétrico. Esto significa que la uniformidad y la simetría son condiciones necesarias para que una gráfica mixta sea euleriana. Sin embargo, esta no es una condición necesaria y suficiente, porque es posible construir una gráfica par y no simétrica que siga siendo euleriana.

Ford y Fulkerson demostraron en 1962 en su libro Flujos en redes una condición necesaria y suficiente para que un grafo sea euleriano, es decir, que cada vértice debe ser par y satisfacer la condición de equilibrio. Para cada subconjunto de vértices S, la diferencia entre el número de arcos que salen de S y entran en S debe ser menor o igual al número de aristas incidentes con S. Esta es la condición del conjunto equilibrado. Una gráfica mixta y fuertemente conexa es euleriana si y sólo si G es par y equilibrado.

El proceso de comprobar si un grafo mixto es euleriano es más difícil que comprobar si un gráfico dirigido o no dirigido es euleriano porque la condición del conjunto equilibrado concierne a todos los subconjuntos posibles de vértices.