Calorimetría

El primer mundo ice-calorimeter, utilizado en el invierno de 1782–83, por Antoine Lavoisier y Pierre-Simon Laplace, para determinar el calor involucrado en varios cambios químicos; cálculos que se basaron en el descubrimiento previo de Joseph Black del calor latente. Estos experimentos marcan la base de la termoquímica.

Snellen cámara de calorías directas, Universidad de Ottawa.

Carrito metabólico de calorías indirectos que mide la absorción de oxígeno y la producción de CO2 de un sujeto que respira espontáneamente (método de dilución con capucha de canopy).

En química y termodinámica, calorimetría (del latín calor 'heat', y griego μέτρον (metron) 'medir') es la ciencia o el acto de medir los cambios en las variables de estado de un cuerpo con el propósito de derivar la transferencia de calor asociada con los cambios de su estado debido, por ejemplo, a reacciones químicas, cambios físicos o transiciones de fase bajo restricciones específicas. La calorimetría se realiza con un calorímetro. Se dice que el médico y científico escocés Joseph Black, quien fue el primero en reconocer la distinción entre calor y temperatura, es el fundador de la ciencia de la calorimetría.

La calorimetría indirecta calcula el calor que producen los organismos vivos midiendo su producción de dióxido de carbono y nitrógeno residual (frecuentemente amoníaco en los organismos acuáticos o urea en los terrestres), o a partir de su consumo de oxígeno. Lavoisier señaló en 1780 que la producción de calor se puede predecir a partir del consumo de oxígeno de esta manera, utilizando regresión múltiple. La teoría del balance energético dinámico explica por qué este procedimiento es correcto. El calor generado por los organismos vivos también puede medirse mediante calorimetría directa, en la que todo el organismo se coloca dentro del calorímetro para la medición.

Un instrumento moderno ampliamente utilizado es el calorímetro diferencial de barrido, un dispositivo que permite obtener datos térmicos en pequeñas cantidades de material. Implica calentar la muestra a una velocidad controlada y registrar el flujo de calor hacia o desde la muestra.

Cálculo calorimétrico clásico del calor

Casos con ecuación de estado diferenciable para un cuerpo de un componente

Cálculo clásico básico con respecto al volumen

La calorimetría requiere que un material de referencia que cambia de temperatura tenga propiedades térmicas constitutivas definidas conocidas. La regla clásica, reconocida por Clausius y Kelvin, es que la presión ejercida por el material calorimétrico está total y rápidamente determinada únicamente por su temperatura y volumen; esta regla es para cambios que no implican un cambio de fase, como el derretimiento del hielo. Hay muchos materiales que no cumplen con esta regla, y para ellos, la fórmula actual de la calorimetría clásica no proporciona una explicación adecuada. Aquí se supone que la regla clásica se cumple para el material calorimétrico que se utiliza, y las proposiciones se escriben matemáticamente:

La respuesta térmica del material calimétrico es completamente descrita por su presión ${displaystyle p}$ como valor de su función constitutiva ${displaystyle p(V,T)}$ de sólo el volumen ${displaystyle V.$ y la temperatura ${displaystyle T.$. Todos los incrementos están aquí obligados a ser muy pequeños. Este cálculo se refiere a un dominio del volumen y la temperatura del cuerpo en el que no se produce ningún cambio de fase, y sólo hay una fase presente. Un supuesto importante aquí es la continuidad de las relaciones de propiedad. Se necesita un análisis diferente para el cambio de fase

Cuando un pequeño aumento de calor se gana por un cuerpo calimétrico, con pequeños incrementos, ${displaystyle delta V}$ de su volumen, y ${displaystyle delta T.$ de su temperatura, el aumento de calor, ${displaystyle delta Q }$, ganado por el cuerpo de material calimétrico, es dado por

${displaystyle delta Q =C_{T} {(V,T),delta V,+,C_{(T)}(V,T),delta T}$

dónde

${fnMicrosoft Sans Serif}$ denota el calor latente con respecto al volumen, del material calorimétrico a temperatura controlada constante ${displaystyle T}$. La presión del entorno sobre el material se ajusta instrumentalmente para imponer un cambio de volumen elegido, con volumen inicial ${displaystyle V.$. Para determinar este calor latente, el cambio de volumen es efectivamente la cantidad instrumentalmente variada. Este calor latente no es uno de los ampliamente utilizados, pero es de interés teórico o conceptual.

${fnMicrosoft Sans Serif}$ denota la capacidad de calor, del material calorimétrico al volumen constante fijo ${displaystyle V.$, mientras que la presión del material se permite variar libremente, con temperatura inicial ${displaystyle T.$. La temperatura se ve obligada a cambiar por exposición a un baño de calor adecuado. Es costumbre escribir ${fnMicrosoft Sans Serif}$ simplemente ${displaystyle C_{V}(V,T) }$, o incluso más brevemente ${displaystyle C_{V}$. Este calor latente es uno de los dos ampliamente utilizados.

El calor latente con respecto al volumen es el calor requerido para el aumento de unidad en volumen a temperatura constante. Se puede decir que está "medido a lo largo de un isotro", y la presión que ejerce el material puede variar libremente, según su ley constitutiva ${displaystyle p=p(V,T)}$. Para un material dado, puede tener un signo positivo o negativo o excepcionalmente puede ser cero, y esto puede depender de la temperatura, como lo hace para el agua alrededor de 4 C. El concepto de calor latente con respecto al volumen fue quizás primero reconocido por Joseph Black en 1762. También se utiliza el término "calor latente de expansión". El calor latente con respecto al volumen también se puede llamar la "energía latente con respecto al volumen". Para todos estos usos de 'calor latente', una terminología más sistemática utiliza 'capacidad de calor latente'.

La capacidad calorífica a volumen constante es el calor requerido por unidad de incremento de temperatura a volumen constante. Se puede decir que se 'medida a lo largo de una isocora' y, de nuevo, se permite que la presión que ejerce el material varíe libremente. Siempre tiene signo positivo. Esto significa que para un aumento en la temperatura de un cuerpo sin cambio de su volumen, se le debe suministrar calor. Esto es consistente con la experiencia común.

Cuantidades como ${displaystyle delta Q }$ a veces se llaman 'diferencias curvas', porque se miden a lo largo de las curvas en los ${displaystyle (V,T)}$ superficie.

Teoría clásica de calorimetría de volumen constante (isocorica)

La calorimetría de volumen constante es una calorimetría realizada a un volumen constante. Esto implica el uso de un calorímetro de volumen constante. El calor todavía se mide por el principio de calorimetría mencionado anteriormente.

Esto significa que en un calórico construido adecuadamente, llamado calórico bomba, el aumento del volumen ${displaystyle delta V}$ puede ser hecho para desaparecer, ${displaystyle delta V=0}$. Para calorías de volumen constante:

${displaystyle delta Q=C_{V}delta T.$

dónde

${displaystyle delta T.$ denota el aumento en temperatura y

${displaystyle C_{V}$ denota la capacidad de calor en volumen constante.

Cálculo clásico del calor con respecto a la presión

De la regla anterior de cálculo del calor con respecto al volumen, se sigue una con respecto a la presión.

En un proceso de pequeños incrementos, ${displaystyle delta p }$ de su presión, y ${displaystyle delta T.$ de su temperatura, el aumento de calor, ${displaystyle delta Q }$, ganado por el cuerpo de material calimétrico, es dado por

${displaystyle delta Q =C_{T} {p)}(p,T),delta p,+,C_{p}{(T)}(p,T),delta T}$

dónde

${fnMicrosoft Sans Serif}$ denota el calor latente con respecto a la presión, del material calimétrico a temperatura constante, mientras que el volumen y la presión del cuerpo se permiten variar libremente, a presión ${displaystyle p}$ y temperatura ${displaystyle T.$;

${fnMicrosoft Sans Serif}$ denota la capacidad de calor, del material calorimétrico a presión constante, mientras que la temperatura y el volumen del cuerpo se permiten variar libremente, a presión ${displaystyle p}$ y temperatura ${displaystyle T.$. Es costumbre escribir ${fnMicrosoft Sans Serif}$ simplemente ${displaystyle C_{p}(p,T)}$, o incluso más brevemente ${displaystyle C_{p}$.

Las nuevas cantidades aquí están relacionadas con las anteriores:

${displaystyle C_{T}{(p)}(p,T)={frac {C_{T}{(V)} {left.{rac {fnMicrosoft Sans Serif}}$

${displaystyle C_{p}{(T)}(p,T)=C_{(T)}(V,T)-C_{T}{(V)}(V,T){frac {left.{cfrac {partial p}{partial T}}}right_{(V,T)} {left.{c}{c}{c]}{c}{c}{c}{c}{c}{c}{c}{c]}{c}{c]}{c}{c}}{c]}{c}}}}}}{c}{c}{c]}{c}}}}}}}}}}}{c}{c}}{c}}}}}}}}}}}{c}}}}}}}}}}}}}}}}{c}}}{c}}}}}}}}} {fnMicrosoft Sans Serif}}$

dónde

${displaystyle left.{frac {partial p}{partial V}right sobre la vida_{(V,T)}}$ denota el derivado parcial de ${displaystyle p(V,T)}$ con respecto a ${displaystyle V.$ evaluados para ${displaystyle (V,T)}$

y

${displaystyle left.{frac {partial p}}right habit_{(V,T)}}$ denota el derivado parcial de ${displaystyle p(V,T)}$ con respecto a ${displaystyle T.$ evaluados para ${displaystyle (V,T)}$.

Los calores latentes ${fnMicrosoft Sans Serif}$ y ${fnMicrosoft Sans Serif}$ son siempre de signo opuesto.

Es común referirse a la relación de calores específicos como

${displaystyle gamma (V,T)={frac {C_{p} {(p,T)}{C_{V}{(T)}}}} {c]}$ a menudo sólo escrito como ${displaystyle gamma ={frac {C_{p} {C_{V}}}$.

Calorimetría a través del cambio de fase, la ecuación de estado muestra una discontinuidad de salto

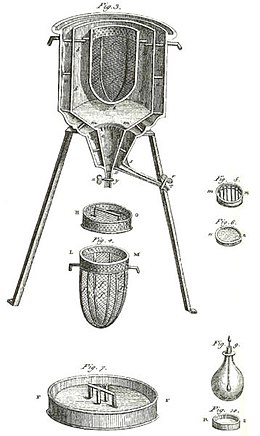
Un calorímetro antiguo fue el utilizado por Laplace y Lavoisier, como se muestra en la figura anterior. Trabajó a temperatura constante ya presión atmosférica. El calor latente involucrado no era entonces un calor latente con respecto al volumen o con respecto a la presión, como en la explicación anterior para la calorimetría sin cambio de fase. El calor latente involucrado en este calorímetro fue con respecto al cambio de fase, que ocurre naturalmente a temperatura constante. Este tipo de calorímetro funcionaba midiendo la masa de agua producida por el derretimiento del hielo, que es un cambio de fase.

Acumulación de calefacción

Para un proceso temporal de calentamiento del material calorimétrico, definido por una progresión articular continua ${displaystyle P(t_{1},t_{2}$ de ${displaystyle V(t)}$ y ${displaystyle T(t)}$, comenzando a tiempo ${displaystyle.$ y terminando a tiempo ${displaystyle.$, se puede calcular una cantidad acumulada de calor entregado, ${displaystyle Delta Q(P(t_{1},t_{2}),}$. Este cálculo se hace por la integración matemática a lo largo de la progresión con respecto al tiempo. Esto se debe a que los incrementos de calor son 'aditivos'; pero esto no significa que el calor es una cantidad conservadora. La idea de que el calor era una cantidad conservadora fue inventada por Lavoisier, y se llama la "teoría calórica"; a mediados del siglo XIX fue reconocida como errónea. Escrito con el símbolo ${displaystyle Delta }$, la cantidad ${displaystyle Delta Q(P(t_{1},t_{2}),}$ no se limita en absoluto a ser un aumento con valores muy pequeños; esto es en contraste con ${displaystyle delta Q }$.

Uno puede escribir

${displaystyle Delta Q(P(t_{1},t_{2})$

${displaystyle =int _{P(t_{1},t_{2}{dot {Q}(t)dt}$

${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft ] {fnMicrosoft ] {f} {f} {fnMicrosoft ]} {fnMicrosoft ]} {f} {fnMicrosoft ] {fnMicrosoft ]} {f} {fnMicrosoft ] {fnMicrosoft ]} {f} {f} {fnMicrosoft ] {fnMicrosoft ] {f}fnMicrosoft ] {fnMicrosoft ]fnMicrosoft ] {f} {fnMicrosoft ]fnMicrosoft ]fnMicrosoft ]fnMicrosoft ]} {fn$.

Esta expresión utiliza cantidades tales como ${fnMicrosoft Sans Serif}$ que se definen en la sección abajo encabezada 'Aspectos matemáticos de las reglas anteriores'.

Aspectos matemáticos de las reglas anteriores

El uso de cantidades "muy pequeñas" como ${displaystyle delta Q }$ está relacionado con el requisito físico de la cantidad ${displaystyle p(V,T)}$ para ser "definido en forma psiquiátrica" por ${displaystyle V.$ y ${displaystyle T.$; tal determinación rapida se refiere a un proceso físico. Estas cantidades 'muy pequeñas' se utilizan en el enfoque Leibniz del cálculo infinitesimal. El enfoque de Newton utiliza 'fluxions' en su lugar, como ${displaystyle {dot {}(t)=left.{frac {dV} {dt} 'justo de la vida_{t}$, lo que hace más obvio que ${displaystyle p(V,T)}$ debe ser "determinado en forma psiquiátrica".

En términos de fluxiones, la primera regla de cálculo anterior se puede escribir

$[displaystyle {dot {}(t) =C_{T}(V,T),{dot {}(t),+,C_{(T)}(V,T),{ dot {}(t)}(t)}$

dónde

${displaystyle t}$ denota el tiempo

${fnMicrosoft Sans Serif}$ denota la tasa de tiempo de calefacción del material calorimétrico a la vez ${displaystyle t}$

${fnMicrosoft Sans Serif}$ denota la velocidad de cambio del volumen del material calimétrico a la vez ${displaystyle t}$

${fnMicrosoft Sans Serif}$ denota la velocidad de cambio de temperatura del material calimétrico.

El aumento ${displaystyle delta Q }$ y la fluxión ${fnMicrosoft Sans Serif}$ se obtienen por un tiempo determinado ${displaystyle t}$ que determina los valores de las cantidades a la derecha de las reglas anteriores. Pero esta no es una razón para esperar que debe existir una función matemática ${displaystyle Q(V,T)}$. Por esta razón, el aumento ${displaystyle delta Q }$ se dice que es un 'diferencial imperfecto' o un 'diferencial inexacto'. Algunos libros indican esto por escrito ${displaystyle q }$ en lugar de ${displaystyle delta Q }$. Además, la notación đQ se utiliza en algunos libros. La preocupación por esto puede llevar a un error.

La cantidad ${displaystyle Delta Q(P(t_{1},t_{2})$ se dice correctamente que es un funcional de la progresión conjunta continua ${displaystyle P(t_{1},t_{2}$ de ${displaystyle V(t)}$ y ${displaystyle T(t)}$, pero, en la definición matemática de una función, ${displaystyle Delta Q(P(t_{1},t_{2})$ no es una función ${displaystyle (V,T)}$. Aunque la fluxión ${fnMicrosoft Sans Serif}$ se define aquí como una función del tiempo ${displaystyle t}$, los símbolos ${displaystyle Q$ y ${displaystyle Q(V,T)}$ respectivamente estar solo no se definen aquí.

Alcance físico de las reglas de calorimetría anteriores

Las reglas anteriores se refieren únicamente a materiales calorimétricos adecuados. Los términos 'rápidamente' y 'muy pequeño' requieren una verificación física empírica del dominio de validez de las reglas anteriores.

Las reglas anteriores para el cálculo del calor pertenecen a la calorimetría pura. No hacen referencia a la termodinámica y en su mayoría se entendieron antes del advenimiento de la termodinámica. Son la base de la 'termo' contribución a la termodinámica. La 'dinámica' la contribución se basa en la idea de trabajo, que no se utiliza en las reglas de cálculo anteriores.

Coeficientes convenientemente medidos experimentalmente

Empíricamente, es conveniente medir las propiedades de los materiales calorimétricos bajo condiciones controladas experimentalmente.

Aumento de presión a volumen constante

Para mediciones a un volumen controlado experimentalmente, se puede usar la suposición, mencionada anteriormente, de que la presión del cuerpo del material calorimétrico se puede expresar como una función de su volumen y temperatura.

Para la medición a un volumen constante controlado experimentalmente, el coeficiente isocórico de aumento de presión con la temperatura se define mediante

${displaystyle alpha _{V}(V,T) {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {cfrac {fnMicrosoft Sans Serif}$

Expansión a presión constante

Para mediciones a presión controlada experimentalmente, se supone que el volumen ${displaystyle V.$ del cuerpo de material calimétrico se puede expresar como una función ${displaystyle V(T,p)}$ de su temperatura ${displaystyle T.$ y presión ${displaystyle p}$. Esta suposición está relacionada con, pero no es la misma que, la suposición anterior utilizada que la presión del cuerpo de material calimétrico se conoce como una función de su volumen y temperatura; el comportamiento anómalo de los materiales puede afectar esta relación.

La cantidad que se mide convenientemente a presión constante controlada experimentalmente, el coeficiente de expansión de volumen isobárico, se define por

${displaystyle beta _{p}(T,p) ={frac {1}{V(T,p)}}{left.{cfrac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}$

Compresibilidad a temperatura constante

Para mediciones a temperatura controlada experimentalmente, se vuelve a suponer que el volumen ${displaystyle V.$ del cuerpo de material calimétrico se puede expresar como una función ${displaystyle V(T,p)}$ de su temperatura ${displaystyle T.$ y presión ${displaystyle p}$, con los mismos provisos que se mencionan anteriormente.

La cantidad que se mide convenientemente a temperatura constante controlada experimentalmente, la compresibilidad isotérmica, se define por

${displaystyle kappa _{T}(T,p) {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}$

Relación entre magnitudes calorimétricas clásicas

Suponiendo que la regla ${displaystyle p=p(V,T)}$ es conocido, uno puede derivar la función de ${fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} p}{partial T}$ que se utiliza arriba en el cálculo de calor clásico con respecto a la presión. Esta función se puede encontrar experimentalmente desde los coeficientes ${displaystyle beta _{p}(T,p) }$ y ${displaystyle kappa _{T}(T,p) }$ a través de la relación matemáticamente deducible

${fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} p}{partial T}={frac {beta _{p} {kappa _{T}}}$.

Conexión entre calorimetría y termodinámica

La termodinámica se desarrolló gradualmente durante la primera mitad del siglo XIX, basándose en la teoría de la calorimetría anterior que se había desarrollado antes y en otros descubrimientos. Según Gislason y Craig (2005): "La mayoría de los datos termodinámicos provienen de la calorimetría..." Según Kondepudi (2008): "La calorimetría es ampliamente utilizada en los laboratorios actuales."

En términos de termodinámica, la energía interna ${displaystyle U$ del material calimétrico se puede considerar como el valor de una función ${displaystyle U(V,T)}$ de ${displaystyle (V,T)}$, con derivados parciales ${fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} ¿Qué?$ y ${fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} ¿Qué?$.

Entonces se puede demostrar que se puede escribir una versión termodinámica de las reglas calorimétricas anteriores:

${displaystyle delta Q =left[p(V,T),+,left.{frac {partial U}{partial V}}right sobre la vida_{(V,T)}right],delta V,+,left. T}$

con

${displaystyle C_{T}{(V)}(V,T)=p(V,T),+,left.{frac {partial U}{partial V}}right eterna_{(V,T)} }$

y

${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}$.

Una vez más, en términos de termodinámica, la energía interna ${displaystyle U$ del material calimétrico puede a veces, dependiendo del material calimétrico, ser considerado como el valor de una función ${displaystyle U(p,T)}$ de ${displaystyle (p,T)}$, con derivados parciales ${displaystyle {frac {partial U}{partial p}$ y ${fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} ¿Qué?$, y con ${displaystyle V.$ ser expresible como el valor de una función ${displaystyle V(p,T)}$ de ${displaystyle (p,T)}$, con derivados parciales ${fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} V}{partial p}$ y ${fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} V. T}$.

Entonces, según Adkins (1975), se puede demostrar que se puede escribir una versión termodinámica adicional de las reglas calorimétricas anteriores:

${displaystyle delta ¿Qué?$

con

${displaystyle C_{T}{(p)}(p,T)=left.{frac {partial U}{partial p}}}right imper_{(p,T)},+,pleft.{frac {partial V}{partial p}}}{(p,T)} }$

y

${displaystyle C_{p} {p,T)=left.{frac {partial U}{partial T}}}right imper_{(p,T)},+,pleft.{frac {partial V}{partial T}}}}}justo, t)}$.

Más allá del hecho calimétrico señalado arriba que los calores latentes ${fnMicrosoft Sans Serif}$ y ${fnMicrosoft Sans Serif}$ son siempre de signo opuesto, se puede mostrar, utilizando el concepto termodinámico del trabajo, que también

${displaystyle C_{T} {V,T),left.{frac {partial p}{partial T}}right imper_{(V,T)}geq 0,}$

Especial interés de la termodinámica en calorimetría: los segmentos isotérmicos de un ciclo de Carnot

La calorimetría tiene un beneficio especial para la termodinámica. Habla del calor absorbido o emitido en el segmento isotérmico de un ciclo de Carnot.

Un ciclo de Carnot es un tipo especial de proceso cíclico que afecta a un cuerpo compuesto de material adecuado para su uso en un motor térmico. Tal material es del tipo considerado en calorimetría, como se señaló anteriormente, que ejerce una presión que se determina muy rápidamente solo por la temperatura y el volumen. Se dice que tal cuerpo cambia reversiblemente. Un ciclo de Carnot consta de cuatro etapas o segmentos sucesivos:

(1) un cambio en el volumen de un volumen ${displaystyle V_{a}$ a un volumen ${displaystyle V_{b}$ a temperatura constante ${displaystyle T^{+}$ para incurrir en un flujo de calor en el cuerpo (conocido como un cambio isotérmico)

2) un cambio de volumen ${displaystyle V_{b}$ a un volumen ${displaystyle V_{c}$ a una temperatura variable tal como no incurre ningún flujo de calor (conocido como un cambio adiabático)

(3) otro cambio isotérmico del volumen ${displaystyle V_{c}$ a un volumen ${displaystyle V_{d}$ a temperatura constante ${displaystyle T^{-}$ tales como incurrir en un flujo o calor fuera del cuerpo y tal como prepararse precisamente para el siguiente cambio

(4) otro cambio adiabático del volumen ${displaystyle V_{d}$ volver a ${displaystyle V_{a}$ tal como devolver el cuerpo a su temperatura inicial ${displaystyle T^{+}$.

En el segmento isotérmico (1), el calor que fluye hacia el cuerpo viene dado por

${displaystyle Delta Q(V_{a},V_{b};T^{+}) ,=,,,,,,, ¿Qué?$

y en el segmento isotérmico (3) el calor que sale del cuerpo viene dado por

${displaystyle -Delta Q(V_{c},V_{d};T^{-}),=,-int ¿Qué?$.

Debido a que los segmentos (2) y (4) son adiabáticas, no fluye calor dentro ni fuera del cuerpo durante ellos y, en consecuencia, el calor neto suministrado al cuerpo durante el ciclo viene dado por

${displaystyle Delta Q(V_{a},V_{b};T^{+};V_{c},V_{d};T^{-}),=, Delta Q(V_{a},V_{b};T^{+}),+, Delta Q(V_{c},V_{d};T^{-}),=,int ¿Por qué? ¿Qué?$.

Esta cantidad es utilizada por la termodinámica y se relaciona de manera especial con el trabajo neto realizado por el cuerpo durante el ciclo de Carnot. El cambio neto de la energía interna del cuerpo durante el ciclo de Carnot, ${displaystyle Delta U(V_{a},V_{b};T^{+};V_{c},V_{d};T^{-}) }$, es igual a cero, porque el material del cuerpo de trabajo tiene las propiedades especiales señaladas anteriormente.

Especial interés de la calorimetría en termodinámica: relaciones entre magnitudes calorimétricas clásicas

Relación del calor latente con respecto al volumen y la ecuación de estado

La cantidad ${fnMicrosoft Sans Serif}$, el calor latente con respecto al volumen, pertenece a la calorías clásica. Cuenta la ocurrencia de transferencia de energía por trabajo en un proceso en el que también se transfiere calor; la cantidad, sin embargo, se consideró antes de que la relación entre el calor y las transferencias de trabajo se aclarara por la invención de la termodinámica. A la luz de la termodinámica, la cantidad calimétrica clásica se revela estando estrechamente vinculada a la ecuación de estado del material calimétrico ${displaystyle p=p(V,T)}$. Siempre que la temperatura ${displaystyle T,}$ se mide en la escala absoluta termodinámica, la relación se expresa en la fórmula

${displaystyle C_{T}{(V)}(V,T)=Tleft.{frac {partial p}{partial T}}right imper_{(V,T)}$.

Diferencia de calores específicos

La termodinámica avanzada proporciona la relación

${displaystyle C_{p}(p,T)-C_{V}=left[p(V,T),+,left.{frac {partial U}{partial V}right _{,T}}derecho.$.

A partir de esto, un razonamiento matemático y termodinámico adicional lleva a otra relación entre cantidades calorimétricas clásicas. La diferencia de calores específicos está dada por

${displaystyle C_{p}(p,T)-C_{V}(V,T)={frac {TV,beta _{p}{2}(T,p)}{kappa _{T} {T}}}}}} {}}}}} {f}$.

Práctica calorimetría de volumen constante (calorimetría de bomba) para estudios termodinámicos

La calorimetría de volumen constante es una calorimetría realizada a un volumen constante. Esto implica el uso de un calorímetro de volumen constante.

No se realiza trabajo en calorimetría de volumen constante, por lo que el calor medido es igual al cambio en la energía interna del sistema. Se supone que la capacidad calorífica a volumen constante es independiente de la temperatura.

El calor se mide por el principio de la calorimetría.

${displaystyle q=C_{V}Delta T=Delta U,}$

dónde

ΔU es el cambio en la energía interna,

ΔT es el cambio de temperatura y

C_V es la capacidad de calor en volumen constante.

En calorimetría de volumen constante la presión no se mantiene constante. Si hay una diferencia de presión entre los estados inicial y final, el calor medido necesita un ajuste para proporcionar el cambio de entalpía. Uno entonces tiene

${displaystyle Delta H=Delta U+Delta (PV)= Delta U+VDelta P,}$

dónde

ΔH es el cambio en la enthalpy y

V es el volumen inmutable de la cámara de muestra.

Libros

• Adkins, C.J. (1975). Equilibrium Thermodynamics, segunda edición, McGraw-Hill, Londres, ISBN 0-07-084057-1.
• Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics, New York, ISBN 0-88318-797-3.
• Bryan, G.H. (1907). Termodinámica. Un tratado introductorio que se ocupa principalmente de los primeros principios y sus aplicaciones directasB.G. Tuebner, Leipzig.
• Callen, H.B. (1960/1985). La termodinámica y una introducción a la termoestadística, segunda edición, Wiley, Nueva York, ISBN 981-253-185-8.
• Crawford, F.H. (1963). Calor, termodinámica y Física Estadística, Rupert Hart-Davis, Londres, Harcourt, Brace, & World.
• Guggenheim, E.A. (1949/1967). Termodinámica. Tratamiento avanzado para los químicos y los físicos, North-Holland, Amsterdam.
• Iribarne, J.V., Godson, W.L. (1973/1981), Termodinámica atmosférica, segunda edición, D. Reidel, Kluwer Academic Publishers, Dordrecht, ISBN 90-277-1296-4.
• Kondepudi, D. (2008). Introducción a la termodinámica modernaWiley, Chichester, ISBN 978-0-470-01598-8.
• Landsberg, P.T. (1978). Termodinámica y Mecánica Estadística, Oxford University Press, Oxford, ISBN 0-19-851142-6.
• Lewis, G.N., Randall, M. (1923/1961). Termodinámica, segunda edición revisada por K.S Pitzer, L. Brewer, McGraw-Hill, Nueva York.
• Maxwell, J.C. (1872). Teoría de Calor, tercera edición, Longmans, Green y Co., Londres.
• Partington, J.R. (1949). Un tratado avanzado sobre la química física, Volumen 1, Principios fundamentales. Las propiedades de los gasesLongmans, Green y Co., Londres.
• Planck, M. (1923/1926). Treatise on Thermodynamics, tercera edición en inglés traducida por A. Ogg de la séptima edición alemana, Longmans, Green & Co., Londres.
• Truesdell, C., Bharatha, S. (1977). Los conceptos y la lógica de la termodinámica clásica como Teoría de los motores de calor, Rigorously Construido sobre la Fundación Laid por S. Carnot y F. Reech, Springer, Nueva York, ISBN 0-387-07971-8.