Cálculo multivariable

Cálculo multivariable (también conocido como cálculo multivariado) es la extensión del cálculo en una variable al cálculo con funciones de varias variables: la diferenciación e integración de funciones que involucran múltiples variables (multivariadas), en lugar de solo una.

El cálculo multivariable puede considerarse una parte elemental del cálculo avanzado. Para cálculo avanzado, consulte cálculo en el espacio euclidiano. El caso especial del cálculo en el espacio tridimensional suele denominarse cálculo vectorial.

Operaciones típicas

Límites y continuidad

Un estudio de los límites y la continuidad en el cálculo multivariable produce muchos resultados contrarios a la intuición que no se demuestran mediante funciones de una sola variable. Por ejemplo, hay funciones escalares de dos variables con puntos en su dominio que dan límites diferentes cuando se abordan por caminos diferentes. Por ejemplo, la función.

${displaystyle f(x,y)={frac {fnK}} {fnK}}}$

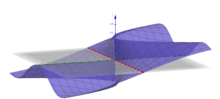
enfoques cero cuando el punto ${displaystyle (0,0)}$ se aborda en línea a través del origen (${displaystyle y=kx}$). Sin embargo, cuando se aborda el origen a lo largo de una parabola ${displaystyle y=pm x^{2}$, el valor de la función tiene un límite ${displaystyle pm 1/2}$. Dado que tomar diferentes caminos hacia el mismo punto produce diferentes valores límite, no existe un límite general allí.

La continuidad en cada argumento no es suficiente para continuidad multivariada también se puede ver desde el siguiente ejemplo. En particular, para una función de valor real con dos parámetros de valor real, ${displaystyle f(x,y)}$, continuidad de ${displaystyle f}$ dentro ${displaystyle x}$ fija ${displaystyle y}$ y continuidad de ${displaystyle f}$ dentro ${displaystyle y}$ fija ${displaystyle x}$ no implica la continuidad de ${displaystyle f}$.

Considere

${displaystyle f(x,y)={begin{cases}{frac {y}{x}-y limit {text{if}quad 0leq y Seguido 0leq 1\\\\\\\\\\\\\\\\\\\\\\\\\cH00}\\fn}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn}}\fn}}}}}}}}}}}}}}}}}\\\\\\\\\\\\\ {x}{y}}-x limit {text{if}quad 0leq x Secundy111-x limitada{if}quad 0sec=y$