Calculador escalonado

El calculador escalonado o calculadora Leibniz fue una calculadora mecánica inventada por el matemático alemán Gottfried Wilhelm Leibniz alrededor de 1672 y terminada en 1694. El nombre proviene de la traducción del Término alemán para su mecanismo operativo, Staffelwalze, que significa "tambor escalonado". Fue la primera calculadora que podía realizar las cuatro operaciones aritméticas básicas.

Sin embargo, su intrincado engranaje de precisión estaba algo más allá de la tecnología de fabricación de la época; Los problemas mecánicos, además de un defecto de diseño en el mecanismo de transporte, impidieron que las máquinas funcionaran de manera confiable.

Se construyeron dos prototipos; hoy sólo sobrevive uno en la Biblioteca Nacional de Baja Sajonia (Niedersächsische Landesbibliothek) en Hannover, Alemania. Se exhiben varias réplicas posteriores, como la del Deutsches Museum de Múnich. A pesar de los defectos mecánicos del calculador escalonado, sugirió posibilidades a los futuros constructores de calculadoras. El mecanismo operativo, inventado por Leibniz, llamado cilindro escalonado o rueda de Leibniz, se utilizó en muchas máquinas calculadoras durante 200 años, y hasta la década de 1970 con la calculadora manual Curta.

Descripción

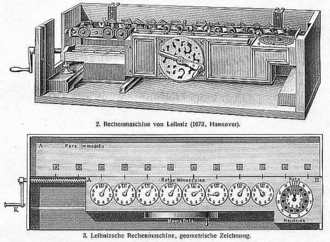
El calculador escalonado se basó en un mecanismo de engranajes que inventó Leibniz y que ahora se llama rueda de Leibniz. No está claro cuántas variantes diferentes de la calculadora se fabricaron. Algunas fuentes, como el dibujo de la derecha, muestran una versión de 12 dígitos. Esta sección describe el prototipo de 16 dígitos que se conserva en Hannover.

La máquina mide unos 67 cm (26 pulgadas) de largo, está hecha de latón pulido y acero y está montada en una caja de roble. Consta de dos partes paralelas adjuntas: un acumulador, que puede considerarse como un registro acumulador que se encuentra en arquitecturas de conjuntos de instrucciones de procesadores más antiguos, una sección en la parte posterior, que puede contener 16 dígitos decimales, y una sección de entrada de 8 dígitos para El frente. La sección de entrada tiene 8 diales con perillas para configurar el número de operando, un dial similar a un teléfono a la derecha para configurar el dígito multiplicador y una manivela en el frente para realizar el cálculo. El resultado aparece en las 16 ventanas de la sección del acumulador trasero. La sección de entrada está montada sobre rieles y se puede mover a lo largo de la sección del acumulador con una manivela en el extremo izquierdo que hace girar un engranaje helicoidal, para cambiar la alineación de los dígitos del operando con los dígitos del acumulador. También hay un indicador de acarreo de decenas y un control para poner la máquina a cero. La máquina puede:

• añadir o restar un número de 8 dígitos a/desde un número de 16 dígitos,
• multiplicar dos números de 8 dígitos para obtener un resultado de 16 dígitos,
• dividir un número de 16 dígitos por un divisor de 8 dígitos.

La suma o resta se realiza en un solo paso, con un giro de manivela. La multiplicación y la división se realizan dígito por dígito en los dígitos del multiplicador o divisor, en un procedimiento equivalente a los procedimientos familiares de multiplicación y división larga que se enseñan en la escuela. Las secuencias de estas operaciones se pueden realizar en el número del acumulador; por ejemplo, puede calcular raíces mediante una serie de divisiones y sumas.

Historia

Leibniz tuvo la idea de una máquina calculadora en 1672 en París, a partir de un podómetro. Más tarde conoció la máquina de Blaise Pascal cuando leyó los Pensamientos de Pascal. Se concentró en expandir el mecanismo de Pascal para que pudiera multiplicarse y dividirse. Presentó un modelo de madera a la Royal Society de Londres el 1 de febrero de 1673 y recibió mucho apoyo. En una carta del 26 de marzo de 1673 a Johann Friedrich, donde mencionaba la presentación en Londres, Leibniz describió el propósito de la "máquina aritmética" como hacer cálculos "leicht, geschwind, gewiß" [sic], es decir, fácil, rápido y confiable. Leibniz también añadió que, en teoría, los números calculados podrían ser tan grandes como se deseara, si se ajustara el tamaño de la máquina; cita: "eine zahl von einer ganzen Reihe Ziphern, sie sey so lang sie wolle (nach proporcional der größe der Machine)" [sic]. En inglés: "un número que consta de toda una serie de cifras, siempre que sea (en proporción al tamaño de la máquina)". Su primera máquina preliminar de latón se construyó entre 1674 y 1685. La llamada máquina más antigua se construyó entre 1686 y 1694. La "máquina más joven", la máquina superviviente, se construyó entre 1690 y 1720.

En 1775, la 'máquina más joven' Fue enviado a la Universidad de Göttingen para su reparación y quedó olvidado hasta 1876, cuando un equipo de trabajadores lo encontró en el ático de un edificio universitario en Göttingen. Fue devuelto a Hannover en 1880. De 1894 a 1896, Artur Burkhardt, fundador de una importante empresa de calculadoras alemana, lo restauró y desde entonces se conserva en la biblioteca Gottfried Wilhelm Leibniz.

Operación

La máquina realiza multiplicaciones por sumas repetidas y divisiones por restas repetidas. La operación básica que se realiza es sumar (o restar) el número del operando al registro del acumulador, tantas veces como se desee (para restar, se gira la manivela de operación en la dirección opuesta). El número de sumas (o restas) se controla mediante el dial multiplicador. Funciona como un dial de teléfono, con diez agujeros en su circunferencia numerados del 0 al 9. Para multiplicar por un solo dígito, del 0 al 9, se inserta un lápiz con forma de perilla en el orificio correspondiente del dial y se gira la manivela. El dial multiplicador gira en el sentido de las agujas del reloj y la máquina realiza una suma por cada orificio, hasta que el lápiz toca un tope en la parte superior del dial. El resultado aparece en las ventanas del acumulador. Las restas repetidas se hacen de manera similar, excepto que el dial multiplicador gira en la dirección opuesta, por lo que se usa un segundo conjunto de dígitos, en rojo. Para realizar una única suma o resta, el multiplicador simplemente se establece en uno.

Para multiplicar por números mayores a 9:

1. La multiplicación se establece en los diales operandos.
2. El primer dígito (menos significativo) del multiplicador se establece en la esfera del multiplicador como arriba, y la manivela se convierte, multiplicando el operand por ese dígito y poniendo el resultado en el acumulador.
3. La sección de entrada se desplaza un dígito a la izquierda con la manivela final.
4. El siguiente dígito del multiplicador se establece en el dial multiplicador, y la manivela se vuelve a girar, multiplicando el operado por ese dígito y agregando el resultado al acumulador.
5. Los dos pasos anteriores se repiten para cada dígito multiplicador. Al final, el resultado aparece en las ventanas acumuladoras.

De esta forma se puede multiplicar el operando por un número tan grande como se desee, aunque el resultado está limitado por la capacidad del acumulador.

Para dividir por un divisor de varios dígitos, se utiliza este proceso:

1. El dividendo se establece en el acumulador, y el divisor se establece en los diales operandos.
2. La sección de entrada se mueve con la manivela final hasta que los dígitos izquierdos de los dos números se alinean.
3. La manivela de operación se gira y el divisor se resta del acumulador repetidamente hasta que el dígito de la mano izquierda (más significativo) del resultado es 0.si muestra cualquier otro número, es decir, el resto. El número que muestra el dial multiplicador es entonces el primer dígito del cociente.
4. La sección de entrada se cambia a la derecha un dígito.
5. Los dos pasos anteriores se repiten para obtener cada dígito del cociente, hasta que el carruaje de entrada llegue al extremo derecho del acumulador.

Se puede ver que estos procedimientos son solo versiones mecanizadas de división y multiplicación largas.