Bucle de sincronización de fase

AjustarCompartirImprimirCitar

Sistema de control electrónico

Loop de fase analógica más simple

Un bucle de bloqueo de fase o bucle de bloqueo de fase (PLL) es un sistema de control que genera una señal de salida cuya fase está relacionada con la fase de una señal de entrada. Hay varios tipos diferentes; el más simple es un circuito electrónico que consta de un oscilador de frecuencia variable y un detector de fase en un circuito de retroalimentación. La frecuencia y la fase del oscilador se controlan proporcionalmente mediante un voltaje aplicado, de ahí el término oscilador controlado por voltaje (VCO). El oscilador genera una señal periódica de una frecuencia específica, y el detector de fase compara la fase de esa señal con la fase de la señal periódica de entrada, para ajustar el oscilador para mantener las fases coincidentes.

Mantener la fase de entrada y salida al unísono también implica mantener las mismas frecuencias de entrada y salida. En consecuencia, además de sincronizar las señales, un bucle de enganche de fase puede rastrear una frecuencia de entrada o puede generar una frecuencia que sea un múltiplo de la frecuencia de entrada. Estas propiedades se utilizan para la sincronización del reloj de la computadora, la demodulación y la síntesis de frecuencia.

Los bucles de enganche de fase se emplean ampliamente en radio, telecomunicaciones, computadoras y otras aplicaciones electrónicas. Se pueden usar para demodular una señal, recuperar una señal de un canal de comunicación ruidoso, generar una frecuencia estable en múltiplos de una frecuencia de entrada (síntesis de frecuencia) o distribuir pulsos de reloj cronometrados con precisión en circuitos lógicos digitales como microprocesadores. Dado que un solo circuito integrado ahora puede proporcionar un bloque de construcción de bucle de bloqueo de fase completo, la técnica se usa ampliamente en dispositivos electrónicos modernos, con frecuencias de salida desde una fracción de hercio hasta muchos gigahercios.

Historia

El físico holandés Christiaan Huygens observó la sincronización espontánea de relojes de péndulo débilmente acoplados ya en 1673. A principios del siglo XIX, Lord Rayleigh observó la sincronización de tubos de órgano y diapasones débilmente acoplados. En 1919, W. H. Eccles y J. H. Vincent descubrieron que dos osciladores electrónicos que habían sido sintonizados para oscilar a frecuencias ligeramente diferentes pero que estaban acoplados a un circuito resonante pronto oscilarían a la misma frecuencia. La sincronización automática de osciladores electrónicos fue descrita en 1923 por Edward Victor Appleton.

En 1925, David Robertson, primer profesor de ingeniería eléctrica en la Universidad de Bristol, introdujo el bloqueo de fase en el diseño de su reloj para controlar el sonido de la campana Great George en el nuevo Wills Memorial Building. El reloj de Robertson incorporaba un dispositivo electromecánico que podía variar la velocidad de oscilación del péndulo y derivaba señales de corrección de un circuito que comparaba la fase del péndulo con la de un pulso telegráfico entrante desde el Observatorio de Greenwich cada mañana a las 10:00 GMT. Además de incluir equivalentes de cada elemento de un PLL electrónico moderno, el sistema de Robertson se destacó porque su detector de fase era una implementación lógica de relé del detector de fase/frecuencia que no se vio en los circuitos electrónicos hasta la década de 1970.

El trabajo de Robertson es anterior a la investigación de lo que más tarde se denominó bucle de bloqueo de fase en 1932, cuando los investigadores británicos desarrollaron una alternativa al receptor superheterodino de Edwin Armstrong, el homodino o receptor de conversión directa. En el sistema homodino o sincrodino, se sintonizó un oscilador local a la frecuencia de entrada deseada y se multiplicó con la señal de entrada. La señal de salida resultante incluía la información de modulación original. La intención era desarrollar un circuito receptor alternativo que requiriera menos circuitos sintonizados que el receptor superheterodino. Dado que el oscilador local cambiaría rápidamente de frecuencia, se aplicó una señal de corrección automática al oscilador, manteniéndolo en la misma fase y frecuencia de la señal deseada. La técnica fue descrita en 1932, en un artículo de Henri de Bellescize, en la revista francesa L'Onde Électrique.

En los receptores de televisión analógicos desde al menos finales de la década de 1930, los circuitos de barrido horizontal y vertical de bucle de sincronización de fase están sincronizados con los pulsos de sincronización en la señal de transmisión.

ON Semiconductor HC4046A

En 1969, Signetics introdujo una línea de circuitos integrados monolíticos de bajo costo como el NE565, que eran sistemas completos de bucle de bloqueo de fase en un chip, y las aplicaciones de la técnica se multiplicaron. Unos años más tarde, RCA presentó el "CD4046" CMOS Micropower Phase-Locked Loop, que también se convirtió en un popular bloque de construcción de circuitos integrados.

Estructura y función

Los mecanismos de bucle de enganche de fase se pueden implementar como circuitos analógicos o digitales. Ambas implementaciones utilizan la misma estructura básica. Los circuitos PLL analógicos incluyen cuatro elementos básicos:

Detector de fase
Filtro de paso bajo
oscilador controlado por tensión
Vía de retroalimentación, que puede incluir un separador de frecuencia

Variaciones

Hay varias variaciones de PLL. Algunos términos que se utilizan son "bucle de bloqueo de fase analógico" (APLL), también conocido como bucle de bloqueo de fase lineal" (LPLL), "bucle de enganche de fase digital" (DPLL), "bucle de enganche de fase completamente digital" (ADPLL) y "bucle de bloqueo de fase de software" (SPLL).

PLL analógica o lineal (APLL): El detector de fase es un multiplicador analógico. El filtro de bucle es activo o pasivo. Utiliza un oscilador controlado por tensión (VCO). APLL se dice que es un Tipo II si su filtro de bucle tiene función de transferencia con exactamente un poste en el origen (ver también la conjetura de Egan en el rango de pull-in del tipo II APLL).
PLL digital (DPLL): Un PLL analógico con un detector de fase digital (como XOR, JK afilado, detector de frecuencias de fase). Puede tener divisor digital en el bucle.
Todos los PLL digitales (ADPLL): Detector de fase, filtro y oscilador son digitales. Utiliza un oscilador controlado numéricamente (NCO).
Software PLL (SPLL): Los bloques funcionales son implementados por software en lugar de hardware especializado.
PLL de carga (CP-PLL): CP-PLL es una modificación de bucles bloqueados por fase con detector de frecuencias de fase y señales de onda cuadrada. Vea también la conjetura de Gardner en CP-PLL.

Parámetros de rendimiento

Escribe y orden.
Rangos de frecuencia: rango de sujeción (rango de seguimiento), rango de acceso (rango de captura, rango de adquisición), rango de bloqueo. Vea también el problema de Gardner en el rango de bloqueo, la conjetura de Egan en el rango de entrada de tipo II APLL.
Loop bandwidth: Definir la velocidad del circuito de control.
Respuesta transitoria: Como overshoot y ajustar el tiempo a cierta precisión (como 50 ppm).
Errores Steady-state: Como el error de fase o tiempo restante.
Pureza del espectro de salida: Como bandas laterales generadas a partir de una cierta onda de voltaje VCO.
Racionalidad: Definido por la energía del ruido en una determinada banda de frecuencia (como 10 kHz offset de portador). Altamente dependiente del ruido de fase VCO, ancho de banda PLL, etc.
Parámetros generales: tales como consumo de energía, rango de tensión de suministro, amplitud de salida, etc.

Aplicaciones

Los bucles de sincronización de fase se utilizan ampliamente para fines de sincronización; en comunicaciones espaciales para demodulación coherente y extensión de umbral, sincronización de bits y sincronización de símbolos. Los bucles de enganche de fase también se pueden utilizar para demodular señales moduladas en frecuencia. En los transmisores de radio, se utiliza un PLL para sintetizar nuevas frecuencias que son un múltiplo de una frecuencia de referencia, con la misma estabilidad que la frecuencia de referencia.

Otras aplicaciones incluyen:

Demodulación de la modulación de frecuencia (FM): Si PLL está bloqueado a una señal FM, el VCO rastrea la frecuencia instantánea de la señal de entrada. El voltaje de error filtrado que controla la VCO y mantiene bloqueo con la señal de entrada es demodulado salida FM. Las características de transferencia VCO determinan la linealidad de los demodulados. Dado que el VCO utilizado en un circuito integrado PLL es altamente lineal, es posible realizar demoduladores FM altamente lineales.
Demodulation of frequency-shift keying (FSK): En la comunicación de datos digitales y periféricos informáticos, los datos binarios se transmiten mediante una frecuencia de portador que se desplaza entre dos frecuencias preestablecidas.
Recuperación de pequeñas señales que de otro modo se perderían en el ruido (amplificador de bloqueo para rastrear la frecuencia de referencia)
Recuperación de la información del tiempo del reloj de un flujo de datos como desde una unidad de disco
Multiplicadores de bloqueo en microprocesadores que permiten que los elementos del procesador interno funcionen más rápido que las conexiones externas, manteniendo relaciones de tiempo precisas
Demodulación de módems y otras señales de tono para telecomunicaciones y control remoto.
DSP de señales de vídeo; los bucles bloqueados por fase también se utilizan para sincronizar fase y frecuencia a la señal de vídeo analógica de entrada para que pueda ser muestreado y procesado digitalmente
Microscopía de fuerza atómica en modo de modulación de frecuencia, para detectar cambios de la frecuencia de resonancia del cantilever debido a interacciones de punta-superficie
Motor DC

Recuperación de reloj

Algunos flujos de datos, especialmente los flujos de datos en serie de alta velocidad (como el flujo de datos sin procesar del cabezal magnético de una unidad de disco), se envían sin un reloj que los acompañe. El receptor genera un reloj a partir de una referencia de frecuencia aproximada y luego se alinea en fase con las transiciones en el flujo de datos con un PLL. Este proceso se conoce como recuperación de reloj. Para que este esquema funcione, el flujo de datos debe tener una transición con la frecuencia suficiente para corregir cualquier desviación en el oscilador del PLL. Por lo general, se utiliza algún tipo de código de línea, como la codificación 8b/10b, para establecer un límite superior rígido en el tiempo máximo entre transiciones.

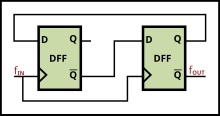
Enderezar

Si se envía un reloj en paralelo con los datos, ese reloj se puede usar para muestrear los datos. Debido a que el reloj debe recibirse y amplificarse antes de que pueda controlar los flip-flops que muestrean los datos, habrá un retardo finito y dependiente del proceso, la temperatura y el voltaje entre el borde del reloj detectado y la ventana de datos recibidos. Este retraso limita la frecuencia con la que se pueden enviar los datos. Una forma de eliminar este retraso es incluir un PLL de desviación en el lado de recepción, de modo que el reloj en cada flip-flop de datos coincida en fase con el reloj recibido. En ese tipo de aplicación, se utiliza con frecuencia una forma especial de PLL llamada bucle de bloqueo de retardo (DLL).

Generación de reloj

Muchos sistemas electrónicos incluyen procesadores de varios tipos que funcionan a cientos de megahercios a gigahercios, muy por encima de las frecuencias prácticas de los osciladores de cristal. Por lo general, los relojes suministrados a estos procesadores provienen de PLL generadores de reloj, que multiplican un reloj de referencia de frecuencia más baja (generalmente 50 o 100 MHz) hasta la frecuencia operativa del procesador. El factor de multiplicación puede ser bastante grande en los casos en que la frecuencia de funcionamiento es de varios gigahercios y el cristal de referencia es solo de decenas o cientos de megahercios.

Espectro ensanchado

Todos los sistemas electrónicos emiten energía de radiofrecuencia no deseada. Varias agencias reguladoras (como la FCC en los Estados Unidos) ponen límites a la energía emitida y cualquier interferencia causada por ella. El ruido emitido generalmente aparece en picos espectrales agudos (generalmente en la frecuencia operativa del dispositivo y algunos armónicos). Un diseñador de sistemas puede usar un PLL de espectro ensanchado para reducir la interferencia con receptores de alto Q al distribuir la energía en una porción más grande del espectro. Por ejemplo, al cambiar la frecuencia operativa hacia arriba y hacia abajo en una pequeña cantidad (alrededor del 1 %), un dispositivo que funciona a cientos de megahercios puede distribuir su interferencia de manera uniforme en unos pocos megahercios de espectro, lo que reduce drásticamente la cantidad de ruido que se ve en la transmisión. Canales de radio FM, que tienen un ancho de banda de varias decenas de kilohercios.

Distribución del reloj

Normalmente, el reloj de referencia ingresa al chip e impulsa un bucle de bloqueo de fase (PLL), que luego impulsa la distribución del reloj del sistema. La distribución del reloj suele estar equilibrada para que el reloj llegue a todos los puntos finales simultáneamente. Uno de esos puntos finales es la entrada de retroalimentación del PLL. La función del PLL es comparar el reloj distribuido con el reloj de referencia entrante y variar la fase y la frecuencia de su salida hasta que los relojes de referencia y de realimentación coincidan en fase y frecuencia.

Los PLL son omnipresentes: sintonizan relojes en sistemas de varios pies de ancho, así como relojes en pequeñas porciones de chips individuales. A veces, es posible que el reloj de referencia no sea realmente un reloj puro, sino un flujo de datos con suficientes transiciones para que el PLL pueda recuperar un reloj normal de ese flujo. A veces, el reloj de referencia tiene la misma frecuencia que el reloj impulsado a través de la distribución del reloj, otras veces, el reloj distribuido puede ser un múltiplo racional de la referencia.

Detección de AM

Se puede usar un PLL para demodular sincrónicamente señales moduladas en amplitud (AM). El PLL recupera la fase y la frecuencia de la portadora de la señal AM entrante. La fase recuperada en el VCO difiere de la del portador en 90°, por lo que se cambia de fase para que coincida y luego se alimenta a un multiplicador. La salida del multiplicador contiene tanto la suma como la diferencia de las señales de frecuencia, y la salida demodulada se obtiene mediante filtrado de paso bajo. Dado que el PLL responde solo a las frecuencias portadoras que están muy cerca de la salida del VCO, un detector PLL AM exhibe un alto grado de selectividad e inmunidad al ruido que no es posible con los demoduladores AM de tipo pico convencionales. Sin embargo, el bucle puede perder el enganche cuando las señales de AM tienen una profundidad de modulación del 100 %.

Reducción de fluctuaciones y ruido

Una propiedad deseable de todos los PLL es que los bordes del reloj de referencia y de retroalimentación estén muy alineados. La diferencia promedio en el tiempo entre las fases de las dos señales cuando el PLL ha logrado el bloqueo se denomina desplazamiento de fase estática (también llamado error de fase de estado estable). La variación entre estas fases se denomina seguimiento de fluctuaciones. Idealmente, la compensación de fase estática debería ser cero y la fluctuación de seguimiento debería ser lo más baja posible.

El ruido de fase es otro tipo de fluctuación que se observa en los PLL y lo provoca el propio oscilador y los elementos utilizados en el circuito de control de frecuencia del oscilador. Se sabe que algunas tecnologías funcionan mejor que otras en este sentido. Los mejores PLL digitales se construyen con elementos lógicos acoplados por emisor (ECL), a expensas de un alto consumo de energía. Para mantener bajo el ruido de fase en los circuitos PLL, es mejor evitar saturar las familias lógicas como la lógica transistor-transistor (TTL) o CMOS.

Otra propiedad deseable de todos los PLL es que la fase y la frecuencia del reloj generado no se vean afectadas por cambios rápidos en los voltajes de las líneas de suministro de energía y tierra, así como el voltaje del sustrato en el que se fabrican los circuitos PLL.. Esto se denomina rechazo del ruido del sustrato y del suministro. Cuanto mayor sea el rechazo de ruido, mejor.

Para mejorar aún más el ruido de fase de la salida, se puede emplear un oscilador bloqueado por inyección siguiendo el VCO en el PLL.

Síntesis de frecuencia

En los sistemas de comunicación inalámbrica digital (GSM, CDMA, etc.), los PLL se utilizan para proporcionar la conversión ascendente del oscilador local durante la transmisión y la conversión descendente durante la recepción. En la mayoría de los teléfonos celulares, esta función se ha integrado en gran medida en un solo circuito integrado para reducir el costo y el tamaño del teléfono. Sin embargo, debido al alto rendimiento requerido de los terminales de las estaciones base, los circuitos de transmisión y recepción se construyen con componentes discretos para lograr los niveles de rendimiento requeridos. Los módulos de oscilador local GSM generalmente se construyen con un circuito integrado de sintetizador de frecuencia y VCO de resonador discreto.

Diagrama de bloques

Esquema de bloque de un bucle bloqueado por fase

El diagrama de bloques que se muestra en la figura muestra una señal de entrada, F_I, que se utiliza para generar una salida, F_O. La señal de entrada a menudo se denomina señal de referencia (también abreviada como F_REF).

En la entrada, un detector de fase (que se muestra como los bloques Detector de frecuencia de fase y Bomba de carga en la figura) compara dos señales de entrada y produce una señal de error que es proporcional a su diferencia de fase. Luego, la señal de error se filtra en paso bajo y se usa para impulsar un VCO que crea una fase de salida. La salida se alimenta a través de un divisor opcional de regreso a la entrada del sistema, lo que produce un bucle de retroalimentación negativa. Si la fase de salida se desvía, la señal de error aumentará, impulsando la fase VCO en la dirección opuesta para reducir el error. Por lo tanto, la fase de salida está bloqueada en la fase de la entrada.

Los bucles de bloqueo de fase analógicos generalmente se construyen con un detector de fase analógico, un filtro de paso bajo y un VCO colocados en una configuración de retroalimentación negativa. Un bucle bloqueado de fase digital utiliza un detector de fase digital; también puede tener un divisor en la ruta de retroalimentación o en la ruta de referencia, o en ambos, para hacer que la frecuencia de la señal de salida del PLL sea un múltiplo racional de la frecuencia de referencia. También se puede crear un múltiplo no entero de la frecuencia de referencia reemplazando el simple contador de división por N en la ruta de retroalimentación con un contador de deglución de pulso programable. Esta técnica generalmente se denomina sintetizador de N fraccional o PLL de N fraccional.

El oscilador genera una señal de salida periódica. Suponga que inicialmente el oscilador tiene casi la misma frecuencia que la señal de referencia. Si la fase del oscilador cae detrás de la de referencia, el detector de fase cambia el voltaje de control del oscilador para que se acelere. Asimismo, si la fase se adelanta a la referencia, el detector de fase cambia el voltaje de control para reducir la velocidad del oscilador. Dado que inicialmente el oscilador puede estar lejos de la frecuencia de referencia, los detectores de fase prácticos también pueden responder a las diferencias de frecuencia, para aumentar el rango de bloqueo de las entradas permitidas. Dependiendo de la aplicación, ya sea la salida del oscilador controlado o la señal de control al oscilador, proporciona la salida útil del sistema PLL.

Elementos

Detector de fase

Un detector de fase (PD) genera un voltaje, que representa la diferencia de fase entre dos señales. En un PLL, las dos entradas del detector de fase son la entrada de referencia y la retroalimentación del VCO. El voltaje de salida de PD se usa para controlar el VCO de modo que la diferencia de fase entre las dos entradas se mantenga constante, lo que lo convierte en un sistema de retroalimentación negativa.

Diferentes tipos de detectores de fase tienen diferentes características de rendimiento.

Por ejemplo, el mezclador de frecuencia produce armónicos que agregan complejidad en aplicaciones donde la pureza espectral de la señal del VCO es importante. Las bandas laterales no deseadas (espurias) resultantes, también llamadas "espolones de referencia" puede dominar los requisitos del filtro y reducir el rango de captura muy por debajo o aumentar el tiempo de bloqueo más allá de los requisitos. En estas aplicaciones se utilizan los detectores de fase digitales más complejos que no tienen un componente de derivación de referencia tan severo en su salida. Además, cuando está bloqueado, la diferencia de fase de estado estable en las entradas que usan este tipo de detector de fase es de cerca de 90 grados.

En las aplicaciones PLL, con frecuencia se requiere saber cuándo el bucle está fuera de bloqueo. Los detectores digitales de frecuencia de fase más complejos suelen tener una salida que permite una indicación fiable de una condición de desbloqueo.

Una puerta XOR se usa a menudo para PLL digitales como un detector de fase efectivo pero simple. También se puede usar en un sentido analógico con solo una ligera modificación en el circuito.

Filtro

El bloque comúnmente llamado filtro de bucle PLL (generalmente un filtro de paso bajo) generalmente tiene dos funciones distintas.

La función principal es determinar la dinámica del bucle, también llamada estabilidad. Así es como el lazo responde a las perturbaciones, como cambios en la frecuencia de referencia, cambios en el divisor de retroalimentación o en el arranque. Las consideraciones comunes son el rango en el que el bucle puede lograr el bloqueo (rango de entrada, rango de bloqueo o rango de captura), la rapidez con que el bucle logra el bloqueo (tiempo de bloqueo, tiempo de bloqueo o tiempo de estabilización) y el comportamiento de amortiguación. Dependiendo de la aplicación, esto puede requerir uno o más de los siguientes: una proporción simple (ganancia o atenuación), una integral (filtro de paso bajo) y/o derivada (filtro de paso alto). Los parámetros de bucle comúnmente examinados para esto son el margen de ganancia y el margen de fase del bucle. Para diseñar esta función se utilizan conceptos comunes en la teoría de control, incluido el controlador PID.

La segunda consideración común es limitar la cantidad de energía de frecuencia de referencia (ondulación) que aparece en la salida del detector de fase que luego se aplica a la entrada de control del VCO. Esta frecuencia modula el VCO y produce bandas laterales de FM comúnmente llamadas "espuelas de referencia".

El diseño de este bloque puede estar dominado por cualquiera de estas consideraciones, o puede ser un proceso complejo que haga malabarismos con las interacciones de los dos. Las compensaciones típicas son: aumentar el ancho de banda generalmente degrada la estabilidad o demasiada amortiguación para una mejor estabilidad reducirá la velocidad y aumentará el tiempo de estabilización. A menudo también se ve afectado el ruido de fase.

Oscilador

Todos los bucles de bloqueo de fase emplean un elemento oscilador con capacidad de frecuencia variable. Puede ser un VCO analógico controlado por circuitos analógicos en el caso de un APLL o controlado digitalmente mediante el uso de un convertidor de digital a analógico, como es el caso de algunos diseños de DPLL. En los ADPLL se utilizan osciladores digitales puros, como un oscilador controlado numéricamente.

Ruta de retroalimentación y divisor opcional

Un ejemplo de divisor digital (por 4) para uso en la ruta de retroalimentación de un PLL multiplicador

Los PLL pueden incluir un divisor entre el oscilador y la entrada de retroalimentación al detector de fase para producir un sintetizador de frecuencia. Un divisor programable es particularmente útil en aplicaciones de transmisores de radio y para el reloj de la computadora, ya que se puede producir una gran cantidad de frecuencias a partir de un solo oscilador de referencia estable, preciso y controlado por cristal de cuarzo (que era costoso antes de que la síntesis hidrotermal a escala comercial proporcionara un oscilador sintético barato). cuarzo).

Algunos PLL también incluyen un divider entre el reloj de referencia y la entrada de referencia al detector de fases. Si el divider en el camino de retroalimentación se divide por $N$ y el divider de entrada de referencia por $M$ , permite al PLL multiplicar la frecuencia de referencia por $N/M$ . Puede parecer más sencillo alimentar al PLL con menor frecuencia, pero en algunos casos la frecuencia de referencia puede ser limitada por otros problemas, y luego el divider de referencia es útil.

La multiplicación de frecuencia también se puede lograr bloqueando la salida del VCO al N armónico de la señal de referencia. En lugar de un simple detector de fase, el diseño utiliza un mezclador armónico (mezclador de muestreo). El mezclador de armónicos convierte la señal de referencia en un tren de impulsos rico en armónicos. La salida del VCO tiene un ajuste grueso para estar cerca de uno de esos armónicos. En consecuencia, la salida deseada del mezclador de armónicos (que representa la diferencia entre el armónico N y la salida del VCO) cae dentro de la banda de paso del filtro de bucle.

También debe tenerse en cuenta que la retroalimentación no se limita a un divisor de frecuencia. Este elemento puede ser otros elementos como un multiplicador de frecuencia o un mezclador. El multiplicador hará que la salida del VCO sea un submúltiplo (en lugar de un múltiplo) de la frecuencia de referencia. Un mezclador puede traducir la frecuencia de VCO por un desplazamiento fijo. También puede ser una combinación de estos. Un ejemplo es un divisor que sigue a un mezclador; esto permite que el divisor funcione a una frecuencia mucho más baja que el VCO sin pérdida de ganancia de bucle.

Modelado

Modelo de dominio de tiempo de APLL

Las ecuaciones que rigen un bucle bloqueado por fases con un multiplicador analógico como el detector de fases y el filtro lineal pueden derivarse de la siguiente manera. Que la entrada al detector de fase sea $f_{1}(theta _{1}(t))$ y la producción de la VCO $f_{2}(theta _{2}(t))$ con fases $theta _{1}(t)$ y $theta _{2}(t)$ . Funciones ${displaystyle f_{1}(theta)}$ y $f_{2}(theta)$ describir ondas de señales. Luego la salida del detector de fases $varphi (t)$ es dado por

{displaystyle varphi (t)=f_{1}(theta _{1}(t))f_{2}(theta _{2}(t))}

La frecuencia VCO generalmente se toma como función de la entrada VCO $g(t)$ como

{displaystyle {dot {theta }}_{2}(t)=omega _{2}(t)=omega _{text{free}}+g_{v}g(t),}

Donde $g_v$ es sensibilidad de la VCO y es expresado en Hz / V; ${displaystyle omega _{text{free}}}$ es una frecuencia de gestión libre de VCO.

El filtro de bucle se puede describir mediante un sistema de ecuaciones diferenciales lineales

{displaystyle {begin{array}{rcl}{dot {x}}&=&Ax+bvarphi (t),\g(t)&=&c^{*}x,end{array}}quad x(0)=x_{0},}

Donde $varphi (t)$ es una entrada del filtro, $g(t)$ es una salida del filtro, $A$ es $n$ -por- $n$ matriz $xin {mathbb {C}}^{n},quad bin {mathbb {R}}^{n},quad cin {mathbb {C}}^{n},quad$ . $x_{0}in {mathbb {C}}^{n}$ representa un estado inicial el filtro. El símbolo estrella es una transposición conyugal.

Por lo tanto, el siguiente sistema describe PLL

{displaystyle {begin{array}{rcl}{dot {x}}&=&Ax+bf_{1}(theta _{1}(t))f_{2}(theta _{2}(t)),\{dot {theta }}_{2}&=&omega _{text{free}}+g_{v}(c^{*}x)\end{array}}quad x(0)=x_{0},quad theta _{2}(0)=theta _{0}.}

Donde $theta _{0}$ es un cambio de fase inicial.

Modelo de dominio de fase de APLL

Considere la entrada de PLL $f_{1}(theta _{1}(t))$ y salida VCO $f_{2}(theta _{2}(t))$ son señales de alta frecuencia. Entonces para cualquier diferente a la pieza $2pi$ - Funciones experimentales $f_{1}(theta)$ y $f_{2}(theta)$ hay una función $varphi (theta)$ tal que el producto $G(t)$ Filtro

{begin{array}{rcl}{dot x}&=&Ax+bvarphi (theta _{1}(t)-theta _{2}(t)),\G(t)&=&c^{{*}}x,end{array}}quad x(0)=x_{0},

en el dominio de fase es asintoticamente igual (la diferencia $G(t)-g(t)$ es pequeño con respecto a las frecuencias) a la salida del filtro en el modelo de dominio del tiempo. Esta función $varphi (theta)$ es una característica del detector de fases.

Denote by $theta _{{Delta }}(t)$ la diferencia de fase

theta _{{Delta }}=theta _{1}(t)-theta _{2}(t).

Entonces el siguiente sistema dinámico describe el comportamiento de PLL

{begin{array}{rcl}{dot x}&=&Ax+bvarphi (theta _{{Delta }}),\{dot theta }_{{Delta }}&=&omega _{{Delta }}-g_{v}(c^{{*}}x).\end{array}}quad x(0)=x_{0},quad theta _{{Delta }}(0)=theta _{{1}}(0)-theta _{2}(0).

Aquí. ${displaystyle omega _{Delta }=omega _{1}-omega _{text{free}}}$ ; $omega _{1}$ es la frecuencia de un oscilador de referencia (suponemos que ${displaystyle omega _{text{free}}}$ es constante).

Ejemplo

Considere las señales sinusoidales

f_{1}(theta _{1}(t))=A_{1}sin(theta _{1}(t)),quad f_{2}(theta _{2}(t))=A_{2}cos(theta _{2}(t))

y un circuito RC simple de un polo como filtro. El modelo en el dominio del tiempo toma la forma

{displaystyle {begin{aligned}{dot {x}}&=-{frac {1}{RC}}x+{frac {1}{RC}}A_{1}A_{2}sin(theta _{1}(t))cos(theta _{2}(t)),\[6pt]{dot {theta }}_{2}&=omega _{text{free}}+g_{v}(c^{*}x)end{aligned}}}

Las características de PD para estas señales son iguales a

varphi (theta _{1}-theta _{2})={frac {A_{1}A_{2}}{2}}sin(theta _{1}-theta _{2})

Por lo tanto, el modelo de dominio de fase toma la forma

{begin{aligned}{dot x}&=-{frac {1}{RC}}x+{frac {1}{RC}}{frac {A_{1}A_{2}}{2}}sin(theta _{{Delta }}),\[6pt]{dot theta }_{{Delta }}&=omega _{{Delta }}-g_{v}(c^{{*}}x).end{aligned}}

Este sistema de ecuaciones es equivalente a la ecuación del péndulo matemático

{begin{aligned}x&={frac {{dot theta }_{2}-omega _{2}}{g_{v}c^{*}}}={frac {omega _{1}-{dot theta }_{{Delta }}-omega _{2}}{g_{v}c^{*}}},\[6pt]{dot x}&={frac {{ddot theta }_{2}}{g_{v}c^{*}}},\[6pt]theta _{1}&=omega _{1}t+Psi\[6pt]theta _{{Delta }}&=theta _{1}-theta _{2},\[6pt]{dot theta }_{{Delta }}&={dot theta }_{1}-{dot theta }_{2}=omega _{1}-{dot theta }_{2},\[6pt]&{frac {1}{g_{v}c^{*}}}{ddot theta }_{{Delta }}-{frac {1}{g_{v}c^{*}RC}}{dot theta }_{{Delta }}-{frac {A_{1}A_{2}}{2RC}}sin theta _{{Delta }}={frac {omega _{2}-omega _{1}}{g_{v}c^{*}RC}}.end{aligned}}

Modelo de dominio de fase linealizado

Los bucles de bloqueo de fase también se pueden analizar como sistemas de control aplicando la transformada de Laplace. La respuesta del bucle se puede escribir como

{frac {theta _{o}}{theta _{i}}}={frac {K_{p}K_{v}F(s)}{s+K_{p}K_{v}F(s)}}

Dónde

$theta _{o}$ es la fase de salida en radians
$theta _{i}$ es la fase de entrada en radians
$K_{p}$ es la ganancia del detector de fases en voltios por radio
$K_{v}$ es la ganancia VCO en radianos por voltio segundo
$F(s)$ es la función de transferencia de filtro de bucle (indimensionable)

Las características del bucle se pueden controlar insertando diferentes tipos de filtros de bucle. El filtro más simple es un circuito RC de un polo. La función de transferencia de bucle en este caso es

F(s)={frac {1}{1+sRC}}

La respuesta del bucle se convierte en:

{frac {theta _{o}}{theta _{i}}}={frac {{frac {K_{p}K_{v}}{RC}}}{s^{2}+{frac {s}{RC}}+{frac {K_{p}K_{v}}{RC}}}}

Esta es la forma de un oscilador armónico clásico. El denominador se puede relacionar con el de un sistema de segundo orden:

s^{2}+2szeta omega _{n}+omega _{n}^{2}

Donde $zeta$ es el factor de amortiguación y $omega _{n}$ es la frecuencia natural del bucle.

Para el filtro RC de un polo,

omega _{n}={sqrt {{frac {K_{p}K_{v}}{RC}}}}

zeta ={frac {1}{2{sqrt {K_{p}K_{v}RC}}}}

La frecuencia natural del bucle es una medida del tiempo de respuesta del bucle, y el factor de amortiguamiento es una medida del sobreimpulso y el zumbido. Idealmente, la frecuencia natural debería ser alta y el factor de amortiguamiento debería estar cerca de 0,707 (amortiguamiento crítico). Con un filtro de un solo polo, no es posible controlar la frecuencia del bucle y el factor de amortiguamiento de forma independiente. Para el caso de amortiguamiento crítico,

RC={frac {1}{2K_{p}K_{v}}}

omega _{c}=K_{p}K_{v}{sqrt {2}}

Un filtro un poco más efectivo, el filtro de adelanto-retardo incluye un polo y un cero. Esto se puede realizar con dos resistencias y un condensador. La función de transferencia para este filtro es

F(s)={frac {1+sCR_{2}}{1+sC(R_{1}+R_{2})}}

Este filtro tiene dos constantes de tiempo

tau _{1}=C(R_{1}+R_{2})

tau _{2}=CR_{2}

Sustituyendo lo anterior se obtiene la siguiente frecuencia natural y factor de amortiguamiento

omega _{n}={sqrt {{frac {K_{p}K_{v}}{tau _{1}}}}}

zeta ={frac {1}{2omega _{n}tau _{1}}}+{frac {omega _{n}tau _{2}}{2}}

Los componentes del filtro de bucle se pueden calcular de forma independiente para una frecuencia natural y un factor de amortiguamiento dados

tau _{1}={frac {K_{p}K_{v}}{omega _{n}^{2}}}

tau _{2}={frac {2zeta }{omega _{n}}}-{frac {1}{K_{p}K_{v}}}

El diseño del filtro de bucle del mundo real puede ser mucho más complejo, p. utilizando filtros de orden superior para reducir varios tipos o fuentes de ruido de fase. (Vea la referencia de D Banerjee a continuación)

Implementación de un bucle de sincronización de fase digital en el software

Los bucles de bloqueo de fase digital se pueden implementar en hardware, utilizando circuitos integrados como un CMOS 4046. Sin embargo, dado que los microcontroladores son cada vez más rápidos, puede tener sentido implementar un bucle de bloqueo de fase en el software para aplicaciones que no requieren bloqueo de señales. en el rango de MHz o más rápido, como controlar con precisión las velocidades del motor. La implementación del software tiene varias ventajas, incluida la fácil personalización del bucle de retroalimentación, incluido el cambio de la relación de multiplicación o división entre la señal que se rastrea y el oscilador de salida. Además, una implementación de software es útil para comprender y experimentar. En MATLAB se presenta un ejemplo de bucle de enganche de fase implementado mediante un detector de frecuencia de fase, ya que este tipo de detector de fase es robusto y fácil de implementar.

% Este ejemplo está escrito en MATLAB% Variables inicialesvcofreq = ceros()1, numiterations);ervec = ceros()1, numiterations);% Realizar un seguimiento de los últimos estados de referencia, señal y señal de errorqsig = 0; qref = 0; Iref = 0; Isig = 0; lersig = 0;ph = 0;freq = 0;% Constantes de filtros de bucle (proporcional y derivativo)% Potencias actuales de dos para facilitar la multiplicación por turnosprop = 1 / 128;deriv = 64;para es = 1:numiterations % Simular un oscilador local usando un contador de 16 bits ph = mod()ph + planta baja()freq / 2 ^ 16), 2 ^ 16); ref = ph . 32768; % Obtener el siguiente valor digital (0 o 1) de la señal para rastrear Sig = tracksig()es); % Implementar el detector de frecuencias de fase rst = ~ ()qsig " qref); % Reiniciar el "flip-flop" de la frecuencia de fase % detector cuando ambas señales y referencias son altas qsig = ()qsig Silencio ()Sig " ~ Isig) " rst; % Trigger señal flip-flop y el borde líder de la señal qref = ()qref Silencio ()ref " ~ Iref) " rst; % Trigger referencia flip-flop en el borde líder de referencia Iref = ref; Isig = Sig; % Guarde estos valores para la próxima iteración (para detección de bordes) ersig = qref - qsig; % Computa la señal de error (si la frecuencia debe aumentar o disminuir) % La señal de error es dada por una o la otra señal de flop % Implementar un filtro post-cero por entrada proporcional y derivada a frecuencia filtered_ersig = ersig + ()ersig - lersig) * deriv; % Mantenga la señal de error para la salida proporcional lersig = ersig; % Integrar la frecuencia VCO utilizando la señal de error freq = freq - 2 ^ 16 * filtered_ersig * prop; % La frecuencia se rastrea como una fracción binaria de punto fijo % Almacene la frecuencia VCO actual vcofreq()1, es) = freq / 2 ^ 16; % Guarde la señal de error para mostrar si la señal o referencia es mayor frecuencia ervec()1, es) = ersig;final

En este ejemplo, se asume que una matriz tracksig contiene una señal de referencia para ser rastreada. El oscilador se implementa mediante un contador, y el bit más significativo del contador indica el estado de encendido/apagado del oscilador. Este código simula los dos flip-flops tipo D que componen un comparador de frecuencia de fase. Cuando la referencia o la señal tienen un borde positivo, el flip-flop correspondiente cambia a nivel alto. Una vez que tanto la referencia como la señal son altas, ambos flip-flops se restablecen. Qué flip-flop es alto determina en ese instante si la referencia o la señal se adelanta a la otra. La señal de error es la diferencia entre estos dos valores de flip-flop. El filtro polo-cero se implementa sumando la señal de error y su derivada a la señal de error filtrada. Este a su vez se integra para encontrar la frecuencia del oscilador.

En la práctica, es probable que se inserten otras operaciones en la retroalimentación de este bucle de bloqueo de fase. Por ejemplo, si el bucle de bloqueo de fase implementara un multiplicador de frecuencia, la señal del oscilador podría dividirse en frecuencia antes de compararla con la señal de referencia.

Analogías prácticas

Analogía de la carrera de automóviles

Como analogía de un PLL, considere una carrera entre dos autos. Uno representa la frecuencia de entrada, el otro la frecuencia del oscilador controlado por voltaje (VCO) de salida del PLL. Cada vuelta corresponde a un ciclo completo. El número de vueltas por hora (una velocidad) corresponde a la frecuencia. La separación de los coches (una distancia) corresponde a la diferencia de fase entre las dos señales oscilantes.

Durante la mayor parte de la carrera, cada auto está solo y libre para adelantar al otro y darle una vuelta al otro. Esto es análogo al PLL en un estado desbloqueado.

Sin embargo, si hay un accidente, se levanta una bandera amarilla de precaución. Esto significa que ninguno de los autos de carrera puede adelantar y adelantar al otro auto. Los dos autos de carrera representan la frecuencia de entrada y salida del PLL en un estado bloqueado. Cada piloto medirá la diferencia de fase (una fracción de la distancia alrededor de la vuelta) entre ellos y el otro auto de carreras. Si el conductor trasero está demasiado lejos, aumentará su velocidad para cerrar la brecha. Si están demasiado cerca del otro automóvil, el conductor reducirá la velocidad. El resultado es que ambos autos de carrera circularán por la pista al unísono con una diferencia de fase fija (o una distancia constante) entre ellos. Dado que ningún automóvil puede dar una vuelta al otro, los automóviles dan la misma cantidad de vueltas en un período de tiempo determinado. Por lo tanto, la frecuencia de las dos señales es la misma.

Analogía del reloj

La fase puede ser proporcional al tiempo, por lo que una diferencia de fase puede ser una diferencia de tiempo. Los relojes están, con diversos grados de precisión, sincronizados en fase (bloqueados en el tiempo) con un reloj guía.

Dejado solo, cada reloj marcará el tiempo a ritmos ligeramente diferentes. Un reloj de pared, por ejemplo, podría adelantarse unos segundos por hora en comparación con el reloj de referencia del NIST. Con el tiempo, esa diferencia horaria sería sustancial.

Para mantener el reloj de pared sincronizado con el reloj de referencia, cada semana el propietario compara la hora de su reloj de pared con un reloj más preciso (una comparación de fase) y reinicia su reloj. Si se deja solo, el reloj de pared seguirá divergiendo del reloj de referencia al mismo ritmo de unos pocos segundos por hora.

Algunos relojes tienen un ajuste de tiempo (un control rápido-lento). Cuando el propietario comparó la hora de su reloj de pared con la hora de referencia, notó que su reloj iba demasiado rápido. En consecuencia, el propietario podría ajustar el tiempo un poco para que el reloj funcione un poco más lento (frecuencia). Si las cosas salen bien, su reloj será más preciso que antes. A lo largo de una serie de ajustes semanales, la noción de un segundo del reloj de pared coincidiría con el tiempo de referencia (bloqueado tanto en frecuencia como en fase dentro de la estabilidad del reloj de pared).

En 1921 se utilizó una versión electromecánica temprana de un bucle sincronizado en fase en el reloj Shortt-Synchronome.

Contenido relacionado

Más resultados...