Bucle costas

A Loop de Costas es un circuito basado en el lazo bloqueado por fase (PLL) que se utiliza para la recuperación de frecuencias de portador de señales de modulación de carrier suprimido (por ejemplo, señales de transmisión suprimidas de banda doble) y señales de modulación de fase (por ejemplo BPSK, QPSK). Fue inventado por John P. Costas en General Electric en la década de 1950. Su invención fue descrita como "un profundo efecto en las comunicaciones digitales modernas". La aplicación primaria de los bucles Costas está en receptores inalámbricos. Su ventaja sobre otros detectores basados en PLL es que en pequeñas desviaciones el voltaje de error del bucle Costas es pecado⁡ ⁡ ()2()Silencio Silencio i− − Silencio Silencio f)){displaystyle sin(2(theta _{i}-theta _{f})} en comparación con pecado⁡ ⁡ ()Silencio Silencio i− − Silencio Silencio f){displaystyle sin(theta _{i}-theta _{f}) }. Esto se traduce en duplicar la sensibilidad y también hace que el bucle de Costas sea único y adecuado para el seguimiento de los transportistas de turno Doppler, especialmente en los receptores OFDM y GPS.

Implementación clásica

El bucle de Costas trabajando en el estado cerrado.

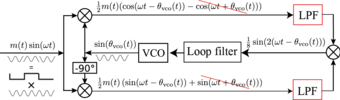
En la implementación clásica de un bucle de Costas, un oscilador controlado por voltaje (VCO) local proporciona salidas en cuadratura, una para cada uno de los dos detectores de fase, por ejemplo,, detectores de producto. La misma fase de la señal de entrada también se aplica a ambos detectores de fase y la salida de cada detector de fase pasa a través de un filtro de paso bajo. Las salidas de estos filtros de paso bajo son entradas a otro detector de fase, cuya salida pasa a través de un filtro de reducción de ruido antes de usarse para controlar el oscilador controlado por voltaje. La respuesta general del bucle está controlada por los dos filtros de paso bajo individuales que preceden al tercer detector de fase, mientras que el tercer filtro de paso bajo cumple una función trivial en términos de ganancia y margen de fase.

La figura anterior de un bucle de Costas se dibuja debajo del "bloqueado" estado, donde la frecuencia del VCO y la frecuencia de la portadora entrante se han vuelto iguales debido al proceso de bucle de Costas. La figura no representa el "desbloqueado" Expresar.

Modelos matemáticos

En el dominio del tiempo

Modelo de dominio del tiempo de BPSK Costas

En el caso más simple m2()t)=1{displaystyle m^{2}(t)=1}. Por lo tanto, m2()t)=1{displaystyle m^{2}(t)=1} no afecta la entrada del filtro de reducción de ruido. Las señales del oscilador (VCO) controlado por el portador y el voltaje son oscilaciones periódicas fref,vco()Silencio Silencio ref,vco()t)){displaystyle f_{ref,vco}(theta _{ref,vco}(t)} con frecuencias altas Silencio Silencio Í Í ref,vco()t){displaystyle { dot {theta }_{ref,vco}(t)}. El bloque ⨂ ⨂ {displaystyle bigotimes } es un multiplicador analógico.

Un filtro lineal se puede describir matemáticamente mediante un sistema de ecuaciones diferenciales lineales:

xÍ Í =Ax+bud()t),uLF=cAlternativa Alternativa x.{displaystyle {begin{ll}{ll}{dot {x}=Ax+bu_{d}(t), sensibleu_{LF}=c^{*}x.end{array}}

Donde A{displaystyle A} es una matriz constante, x()t){displaystyle x(t)} es un vector de estado del filtro, b{displaystyle b} y c{displaystyle c} son vectores constantes.

Por lo general, se supone que el modelo de un VCO es lineal:

Silencio Silencio Í Í vco()t)=⋅ ⋅ vcofree+KvcouLF()t),t▪ ▪ [0,T],{displaystyle {begin{ll}{dot {theta }_{vco}(t)=omega ¿Por qué?

Donde ⋅ ⋅ vcofree{displaystyle omega _{vco}{free}} es la frecuencia de funcionamiento libre de la VCO y Kvco{displaystyle K_{vco} es el factor de ganancia VCO. Asimismo, es posible considerar varios modelos no lineales de VCO.

Supongamos que la frecuencia del generador maestro es constante Silencio Silencio Í Í ref()t)↑ ↑ ⋅ ⋅ ref.{displaystyle { dot {theta }_{ref}(t)equiv omega _{ref}Ecuación del VCO y ecuación del rendimiento del filtro

xÍ Í =Ax+bfref()Silencio Silencio ref()t))fvco()Silencio Silencio vco()t)),Silencio Silencio Í Í vco=⋅ ⋅ vcofree+KvcocAlternativa Alternativa x.{displaystyle {begin{ll}{ll}{dot {x}=Ax+bf_{ref}(theta _{ref}(t))f_{vco}(theta _{vco}(t)), limit{dot {theta }_{vco}=omega ¿Qué?

El sistema no es autónomo y es bastante complicado de investigar.

En el dominio de frecuencia de fase

Modelo de dominio de frecuencia de fase equivalente de Costas

Entrada VCO para el modelo de dominio de frecuencias de fases del bucle Costas

En el caso más simple, cuando

fref()Silencio Silencio ref()t))=#⁡ ⁡ ()⋅ ⋅ reft),fvco()Silencio Silencio vco()t))=pecado⁡ ⁡ ()Silencio Silencio vco()t))fref()Silencio Silencio ref()t))2fvco()Silencio Silencio vco()t))fvco()Silencio Silencio vco()t)− − π π 2)=− − 18()2pecado⁡ ⁡ ()2Silencio Silencio vco()t))+pecado⁡ ⁡ ()2Silencio Silencio vco()t)− − 2⋅ ⋅ reft)+pecado⁡ ⁡ ()2Silencio Silencio vco()t)+2⋅ ⋅ reft)){fnK} {f} {f} {f}} {f}f} {f}}}f}} {big}} {f}} {f}f} {f} {f}}f}}} {f} {f}f}}f}}}f}f}} {f}}}}} {f} {f}}}}}f}}}}}f} {f}}f}}}}}}}}}}}}}}} {f} {f} {f}f}f} {f}}}}}}f}}}}}}}}}}}}}}}}}}}}}}}}}f}f}f}f}f}f}}}f} {f}f} {f}f}}f} {f}}f}}}}}}}}} {1}{8}}{Big (}2sin(2theta _{vco}(t))+sin(2theta _{vco}(t)-2omega _{ref}t)+sin(2theta _{vco}(t)+2omega _{ref}t){Big}}}} {} {}{}{} {}{}{}{}}}}}{}{}}}{}{}{}}{}}}}{}{}{}}}{}{}{}{}{}{}}}}}}}}{}{}}}}}{}{}{}{8} {8} {}}}}}}}}{}}}}{}{}}}{}{}{} {}{}{}}}{}{}}}}}{}{}{}}{}{}{}}}}}{}}}}}}}{}}}}}}}}}}

La suposición de ingeniería estándar es que el filtro elimina la frecuencia superior de la banda lateral de la entrada pero deja la banda lateral inferior sin cambio. Así se supone que la entrada VCO es φ φ ()Silencio Silencio ref()t)− − Silencio Silencio vco()t))=18pecado⁡ ⁡ ()2⋅ ⋅ reft− − 2Silencio Silencio vco()t)).{displaystyle varphi (theta _{ref}(t)-theta _{vco}(t)={frac {1}{8}}sin(2omega _{ref}t-2theta _{vco}(t)). } Esto hace que un bucle de Costas sea equivalente a un bucle bloqueado por fase con característica del detector de fases φ φ ()Silencio Silencio ){displaystyle varphi (theta)} correspondiente a las ondas particulares fref()Silencio Silencio ){displaystyle f_{ref}(theta)} y fvco()Silencio Silencio ){displaystyle f_{vco}(theta)} de las señales de entrada y VCO. Se puede probar que las salidas de filtro en los dominios de tiempo y frecuencia de fase son casi iguales.

Así es posible estudiar el sistema autónomo más simple de ecuaciones diferenciales

xÍ Í =Ax+bφ φ ()Δ Δ Silencio Silencio ),Δ Δ Silencio Silencio Í Í =⋅ ⋅ vcofree− − ⋅ ⋅ ref+KvcocAlternativa Alternativa x,Δ Δ Silencio Silencio =Silencio Silencio vco− − Silencio Silencio ref.{displaystyle {begin{aligned}{dot {x} limit=Ax+bvarphi (Delta theta),\Delta {dot {theta] ♪♪♪ ################################################################################################################################################################################################################################################################ ¿Qué? Delta theta " ¿Qué?.

El método de promediación de Krylov-Bogoliubov permite demostrar que las soluciones de ecuaciones no autónomas y autónomas son cercanas bajo algunos supuestos. Por lo tanto, el diagrama de bloques del bucle de Costas en el dominio del tiempo se puede cambiar asintóticamente al diagrama de bloques en el nivel de las relaciones de fase-frecuencia.

La transición al análisis de un modelo dinámico autónomo del bucle de Costas (en lugar del modelo no autónomo) permite superar las dificultades relacionadas con el modelado del bucle de Costas en el dominio del tiempo, donde se tiene que observar simultáneamente una escala de tiempo muy rápida de las señales de entrada y una escala de tiempo lenta de la fase de la señal. Esta idea hace posible calcular las características principales de rendimiento: rangos de retención, extracción y bloqueo.

Adquisición de frecuencia

Loop Costas antes de la sincronización

Loop de Costas después de la sincronización

Transbordador y señales VCO antes de la sincronización

Entrada VCO durante la sincronización

Transmisores y señales VCO después de la sincronización

El bucle clásico de Costas trabajará para que la diferencia de fase entre la portadora y el VCO se convierta en un valor pequeño, idealmente cero. La pequeña diferencia de fase implica que se ha logrado el bloqueo de frecuencia.

Bucle QPSK Costas

El bucle clásico de Costas se puede adaptar a la modulación QPSK para velocidades de datos más altas.

QPSK clásico Loop de Costas

La señal QPSK de entrada es la siguiente

m1()t)#⁡ ⁡ ()⋅ ⋅ reft)+m2()t)pecado⁡ ⁡ ()⋅ ⋅ reft),m1()t)=± ± 1,m2()t)=± ± 1.{displaystyle m_{1}(t)cos left(omega _{text{ref}tright)+m_{2}(t)sin left(omega _{text{ref}tright),m_{1}(t)=pm 1,m_{2}(t)=pm 1.}

Las entradas de los filtros de paso bajo LPF1 y LPF2 son

φ φ 1()t)=#⁡ ⁡ ()Silencio Silencio vco)()m1()t)#⁡ ⁡ ()⋅ ⋅ reft)+m2()t)pecado⁡ ⁡ ()⋅ ⋅ reft)),φ φ 2()t)=pecado⁡ ⁡ ()Silencio Silencio vco)()m1()t)#⁡ ⁡ ()⋅ ⋅ reft)+m2()t)pecado⁡ ⁡ ()⋅ ⋅ reft)).{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {f} {f} {f}f}f} {f}f}f}f}fnunciof}f}p]

Después de la sincronización, los productos de LPF1 Q()t){displaystyle Q(t)} y LPF2 I()t){displaystyle I(t)} se utilizan para obtener datos demodulados (m1()t){displaystyle m_{1}(t)} y m2()t){displaystyle m_{2}(t)}). Para ajustar la frecuencia de la VCO a la frecuencia de referencia, señales Q()t){displaystyle Q(t)} y I()t){displaystyle I(t)} se limitan y se multiplican:

ud()t)=I()t)Sgn⁡ ⁡ ()Q()t))− − Q()t)Sgn⁡ ⁡ ()I()t)).{displaystyle u_{d}(t)=I(t)operatorname {sgn}(Q(t))-Q(t)operatorname {sgn}(I(t)). }

Entonces la señal ud()t){displaystyle u_{d}(t)} es filtrado por el filtro de bucle y forma la señal de ajuste para el VCO uLF()t){displaystyle u_{text{LF}(t)}, similar al bucle BPSK Costas. Así, QPSK Costas se puede describir por un sistema de ecuaciones diferenciales ordinarias:

xÍ Í 1=ALPFx1+bLPFφ φ 1()t),xÍ Í 2=ALPFx2+bLPFφ φ 2()t),xÍ Í =ALFx+bLF()cLPFAlternativa Alternativa x1Sgn⁡ ⁡ ()cLPFAlternativa Alternativa x2)− − cLPFAlternativa Alternativa x2Sgn⁡ ⁡ ()cLPFAlternativa Alternativa x1)),Silencio Silencio Í Í vco=⋅ ⋅ vcogratis+KVCO()cLFAlternativa Alternativa x+hLF()cLPFAlternativa Alternativa x1Sgn⁡ ⁡ ()cLPFAlternativa Alternativa x2)− − cLPFAlternativa Alternativa x2Sgn⁡ ⁡ ()cLPFAlternativa Alternativa x1))).{displaystyle {begin{aligned}{dot} {x}_{1}===A_{text{LPF}}x_{1}+b_{text{LPF}varphi _{1}(t),\{dot {x}_{2}==A_{text{LPF}}x_{2}+b_{text{LPF}varphi _{2}(t),\{dot {x}} {f} {f} {f} {f}} {big} {big} {big} {f} {f}}f}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fn {fnK} {fnMicrosoft Sans Serif} {fnK}} {fnK} {fnK} {f} {fn}fn}fnfnK} {fnK} {fnK}}} {fnK}}}big)}\\fnKfnKfnKfnKfnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnunc_c_fnun}c_fn ################################################################################################################################################################################################################################################################ ¿Por qué? Big (}c_{text{LF}}{*}x+h_{text{LF}{big (}c_{text{LPF}}}{*}x_{1}operatorname [sgn}(c_{text{LPF}}{*}x_{2})-c_{text{LPF}}^{*}x_{2}operatorname {sgn}(c_{text{LPF}^{*}x_{1}}){big)}{big)}{ Grande.

Aquí. ALPF,bLPF,cLPF{displaystyle A_{text{LPF},b_{text{LPF},c_{text{LPF}} son parámetros de LPF1 y LPF2 y ALF,bLF,cLF,hLF{displaystyle ¿Qué? son parámetros del filtro de bucle.