Bogosort

En informática, bogosort (también conocido como clasificación por permutación, clasificación estúpida, clasificación lenta o bozosort) es un algoritmo de clasificación basado en la generar y probar el paradigma. La función genera sucesivamente permutaciones de su entrada hasta que encuentra una ordenada. No se considera útil para ordenar, pero puede usarse con fines educativos, para contrastarlo con algoritmos más eficientes.

Existen dos versiones de este algoritmo: una versión determinista que enumera todas las permutaciones hasta que encuentra una ordenada y una versión aleatoria que permuta aleatoriamente su entrada. Una analogía para el funcionamiento de la última versión es clasificar una baraja de cartas arrojándola al aire, recogiendo las cartas al azar y repitiendo el proceso hasta que se clasifique la baraja. Su nombre es un acrónimo de las palabras bogus y sort.

Descripción del algoritmo

La siguiente es una descripción del algoritmo aleatorio en pseudocódigo:

mientras no Entendido.
shuffle(deck)

Aquí está el pseudocódigo anterior reescrito en Python 3:

desde al azar importación shuffledef is_sorted()datos) - bool: ""Determine si los datos están ordenados."" retorno Todos()a . b para a, b dentro Cierre()datos, datos[1])def bogosort()datos) - lista: ""Los datos de la rifa hasta que estén ordenados."" mientras no is_sorted()datos): shuffle()datos) retorno datos

Este código asume que data es un simple, mutable, estructura de datos similar a una matriz, como el list—cuyos elementos se pueden comparar sin problemas.

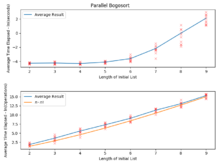
Tiempo de ejecución y terminación

Tiempo de ejecución experimental de bogosort

Si todos los elementos a ordenar son distintos, el número esperado de comparaciones realizadas en el caso promedio por bogosort aleatorio es asintóticamente equivalente a (e − 1)n!, y el número esperado de intercambios en el caso promedio es igual a (n − 1)n!. La cantidad esperada de intercambios crece más rápido que la cantidad esperada de comparaciones, porque si los elementos no están en orden, esto generalmente se descubrirá después de unas pocas comparaciones, sin importar cuántos elementos haya; pero el trabajo de barajar la colección es proporcional a su tamaño. En el peor de los casos, el número de comparaciones e intercambios es ilimitado, por la misma razón por la que una moneda lanzada al aire puede dar cara cualquier número de veces seguidas.

El mejor caso ocurre si la lista dada ya está ordenada; en este caso, el número esperado de comparaciones es n − 1 y no se realizan intercambios.

Para cualquier colección de tamaño fijo, el tiempo de ejecución esperado del algoritmo es finito por la misma razón que se cumple el teorema del mono infinito: existe cierta probabilidad de obtener la permutación correcta, por lo que, dado un número ilimitado de intentos, será casi seguro que eventualmente será elegido.

Algoritmos relacionados

Gorosort

es un algoritmo de clasificación introducido en el 2011 Google Code Jam. Mientras la lista no esté en orden, un subconjunto de todos los elementos es permutado al azar. Si este subconjunto es elegido óptimamente cada vez que se realiza esto, el valor esperado del número total de veces que se necesita realizar esta operación es igual al número de elementos mal colocados.

Bogobogosort

es un algoritmo que fue diseñado para no tener éxito antes de la muerte de calor del universo en cualquier lista sizable. Funciona llamándose recursivamente con copias más pequeñas y más pequeñas del comienzo de la lista para ver si están ordenados. El caso base es un único elemento, que siempre está clasificado. Para otros casos, compara el último elemento con el elemento máximo de los elementos anteriores de la lista. Si el último elemento es mayor o igual, comprueba si el pedido de la copia coincide con la versión anterior, y si es así regresa. De lo contrario, rehúsa la copia actual de la lista y reinicia su cheque recurrente.

Bozosort

es otro algoritmo de clasificación basado en números aleatorios. Si la lista no está en orden, escoge dos elementos al azar y los intercambia, entonces comprueba si la lista está clasificada. El análisis de tiempo de funcionamiento de un bozosort es más difícil, pero algunas estimaciones se encuentran en el análisis de H. Gruber de algoritmos de clasificación "perversamente horribles" aleatorizados. O()n! es el caso promedio esperado.

Worstsort

es un algoritmo de clasificación pessimal que está garantizado para completar en tiempo finito; sin embargo, su eficiencia puede ser arbitrariamente mala, dependiendo de su configuración. El peor algoritmo basado en un algoritmo de clasificación mala, badsort. El algoritmo de badsort acepta dos parámetros: L, que es la lista a ser ordenados, y k, que es una profundidad de recursión. A nivel de recursión k = 0, badsort simplemente utiliza un algoritmo de clasificación común, como el "Bucksort", para ordenar sus entradas y devolver la lista ordenada. Es decir, badsort(L, 0) = grupo de burbujasL). Por lo tanto, la complejidad del tiempo de badsort es O()n²) si k = 0. Sin embargo, para cualquier k ■ 0, badsort(L, k) primero genera P, la lista de todas las permutaciones de L. Entonces, badsort calcula badsort(P, k −1), y devuelve el primer elemento de la orden P. Para hacer peor realmente pesimal, k puede asignarse al valor de una función creciente computable, como f:: N→ → N{displaystyle fcolon mathbb {N} to mathbb {N} (por ejemplo. f()n) A()n, n), donde A es la función de Ackermann). Ergo, para ordenar una lista arbitrariamente mal, se ejecutaría peor surL, f) = mal sur(L, f(longitud(L)), donde longitud(L) es el número de elementos en L. El algoritmo resultante tiene complejidad Ω Ω ()()n!()f()n)))2){textstyle Omega left(left(n!^{(f(n)}right)^{2}right)}, donde n!()m)=()...... ()()n!)!)!...... )!{displaystyle n!^{(m)}=(dotso ((n!)!dotso)!} = factorial de n iterated m veces. Este algoritmo se puede hacer tan ineficiente como uno desea escogiendo una función de crecimiento lo suficientemente rápida f.

Slowsort

es un algoritmo de clasificación humorística diferente que emplea una estrategia de división y conquista errónea para lograr una complejidad masiva.

Quantum Bogosort

es un algoritmo hipotético de clasificación basado en bogosort, creado como un en el juego entre los científicos de la computadora. El algoritmo genera una permutación aleatoria de su entrada usando una fuente cuántica de entropía, comprueba si la lista está ordenada, y, si no lo es, destruye el universo. Suponiendo que la interpretación de muchos mundos tenga, el uso de este algoritmo resultará en al menos un universo sobreviviente donde la entrada fue arreglada con éxito O()n) tiempo.

Milagro

es un algoritmo de clasificación que comprueba si la matriz está ordenada hasta que se produce un milagro. Revise continuamente el array hasta que se ordene, nunca cambie el orden del array. Debido a que el orden nunca se altera, el algoritmo tiene una complejidad hipotética del tiempo O()JUEGO), pero todavía puede ordenar a través de eventos tales como milagros o malestares de un solo evento. Se debe tener especial cuidado en la implementación de este algoritmo ya que los compiladores optimizadores pueden simplemente transformarlo en un bucle de tiempo (verdad).