Bobina de helmholtz

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Dos dispositivos de bobina circular que crea un campo magnético homogéneo

Una bobina de Helmholtz es un dispositivo para producir una región de campo magnético casi uniforme, que lleva el nombre del físico alemán Hermann von Helmholtz. Consta de dos electroimanes colocados en el mismo eje, que transportan una corriente eléctrica igual en la misma dirección. Además de crear campos magnéticos, las bobinas de Helmholtz también se utilizan en aparatos científicos para cancelar campos magnéticos externos, como el campo magnético de la Tierra.

Cuando el par de dos electromagnéticos de una bobina de Helmholtz transporta una corriente eléctrica igual en dirección opuesta, se conoce como bobina anti-Helmholtz, lo que crea una región de gradiente de campo magnético casi uniforme, y se utiliza para crear trampas magnéticas para experimentos de física atómica.

Descripción

Un par de Helmholtz consta de dos bobinas magnéticas circulares idénticas que se colocan simétricamente a lo largo de un eje común, uno a cada lado del área experimental, y separado por una distancia ${displaystyle h}$ igual al radio ${displaystyle R}$ de la bobina. Cada bobina lleva una corriente eléctrica igual en la misma dirección.

Ajuste ${displaystyle h=R}$ , que es lo que define un par de Helmholtz, minimiza la no universalidad del campo en el centro de las bobinas, en el sentido de establecer ${displaystyle partial ^{2}B/partial x^{2}=0}$ (que significa que el primer derivado no cero es ${displaystyle partial ^{4}B/partial x^{4}}$ como se explica a continuación), pero deja aproximadamente 7% de variación en la fuerza de campo entre el centro y los planos de las bobinas. Un valor ligeramente mayor ${displaystyle h}$ reduce la diferencia en el campo entre el centro y los planos de las bobinas, a expensas de empeorar la uniformidad del campo en la región cerca del centro, medida por ${displaystyle partial ^{2}B/partial x^{2}}$ .

Cuando un par de bobinas de Helmholtz llevan una corriente eléctrica igual en la dirección opuesta, crean una región de gradiente de campo magnético casi uniforme. Esto se conoce como bobina anti-Helmholtz, y se utiliza para crear trampas magnéticas para experimentos de física atómica.

En algunas aplicaciones, se utiliza una bobina de Helmholtz para cancelar el campo magnético de la Tierra, produciendo una región con una intensidad de campo magnético mucho más cercana a cero.

Matemáticas

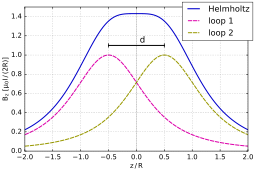
El cálculo del campo magnético exacto en cualquier punto del espacio es matemáticamente complejo e implica el estudio de las funciones de Bessel. Las cosas son más simples a lo largo del eje del coil-pair, y es conveniente pensar en la expansión de la serie Taylor de la fuerza de campo como una función de ${displaystyle x}$ , la distancia desde el punto central del coil-pair a lo largo del eje. Por simetría, los términos de orden extraño en la expansión son cero. Diseñando las bobinas para que el origen ${displaystyle x=0}$ es un punto de inflexión para la fuerza de campo debido a cada bobina por separado, se puede garantizar que el orden ${displaystyle x^{2}}$ term is also cero, and hence the leading non-constant term is of order ${displaystyle x^{4}}$ . El punto de inflexión para una bobina simple se encuentra a lo largo del eje de la bobina a una distancia ${displaystyle R/2}$ desde su centro. Así las ubicaciones para las dos bobinas son ${displaystyle x=pm R/2}$ .

El cálculo que se detalla a continuación proporciona el valor exacto del campo magnético en el punto central. Si el radio es R, el número de vueltas en cada bobina es n y la corriente a través de las bobinas es I, entonces el campo magnético B en el punto medio entre las bobinas estará dado por

{displaystyle B={left({frac {4}{5}}right)}^{3/2}{frac {mu _{0}nI}{R}},}

Donde ${displaystyle mu _{0}}$ es la permeabilidad del espacio libre () ${displaystyle 4pi times 10^{-7}{text{ T}}cdot {text{m/A}}}$ ).

Derivación

Comience con la fórmula para el campo en el eje debido a un bucle de un solo cable que a su vez se deriva de la ley de Biot-Savart:

{displaystyle B_{1}(x)={frac {mu _{0}IR^{2}}{2(R^{2}+x^{2})^{3/2}}}=xi (x){frac {mu _{0}I}{2R}}.}

Aquí

{displaystyle mu _{0};}

= constante de permeabilidad =

{displaystyle 4pi times 10^{-7}{text{ T}}cdot {text{m/A}}=1.257times 10^{-6}{text{ T}}cdot {text{m/A}},}

{displaystyle I;}

= corriente de bobina, en amperios,

{displaystyle R;}

= radio de bobina, en metros,

{displaystyle x;}

= distancia de la bobina, en el eje, a punto, en metros,

{displaystyle xi (x)=[1+(x/R)^{2}]^{-3/2};}

es el coeficiente de distancia dependiente, sin dimensiones.

Las bobinas de Helmholtz constan de n vueltas de cable, por lo que la corriente equivalente en una bobina de una vuelta es n veces la corriente I en la bobina n-vuelta. Al sustituir nI por I en la fórmula anterior se obtiene el campo para una bobina de n vuelta:

{displaystyle B_{1}(x)=xi (x){frac {mu _{0}nI}{2R}}.}

Para ${displaystyle xll R}$ , el coeficiente distancia ${displaystyle xi (x)=[1+(x/R)^{2})]^{-3/2};}$ se puede ampliar en la serie Taylor como:

${displaystyle xi (x)=1-{frac {3}{2}}(x/R)^{2}+{mathcal {O}}((x/R)^{4}).}$

En un par de Helmholtz, las dos bobinas están ubicadas en ${displaystyle x=pm R/2}$ , así que la fuerza del campo B en cualquier ${displaystyle x}$ sería:

{displaystyle {begin{aligned}B(x)&={frac {mu _{0}nI}{2R}}left[xi (x-R/2)+xi (x+R/2)right]&={frac {mu _{0}nI}{2R}}left([1+(x/R-1/2)^{2}]^{-3/2}+[1+(x/R+1/2)^{2}]^{-3/2}right)end{aligned}}}

Los puntos cerca del centro (medio camino entre las dos bobinas) tienen ${displaystyle xll R}$ , y la serie Taylor ${displaystyle xi (x-R/2)+xi (x+R/2)}$ es:

${displaystyle (16{sqrt {5}})/25-(x/R)^{4}(2304{sqrt {5}})/3125+{mathcal {O}}((x/R)^{6})approx 1.43-1.65(x/R)^{4}+{mathcal {O}}((x/R)^{6})}$ .

En un par anti-Helmholtz, la fuerza de campo B en cualquier ${displaystyle x}$ sería:

{displaystyle {begin{aligned}B(x)&={frac {mu _{0}nI}{2R}}left[xi (x-R/2)-xi (x+R/2)right]&={frac {mu _{0}nI}{2R}}left([1+(x/R-1/2)^{2}]^{-3/2}-[1+(x/R+1/2)^{2}]^{-3/2}right)end{aligned}}}

Los puntos cerca del centro (medio camino entre las dos bobinas) tienen ${displaystyle xll R}$ , y la serie Taylor ${displaystyle xi (x-R/2)-xi (x+R/2)}$ es:

${displaystyle (x/R)(96{sqrt {5}})/125-(x/R)^{3}(512{sqrt {5}})/625+{mathcal {O}}((x/R)^{5})approx 1.72(x/R)-1.83(x/R)^{3}+{mathcal {O}}((x/R)^{5})}$ .

Campo magnético variable en el tiempo

La mayoría de las bobinas de Helmholtz utilizan corriente continua (directa) para producir un campo magnético estático. Muchas aplicaciones y experimentos requieren un campo magnético variable en el tiempo. Estas aplicaciones incluyen pruebas de susceptibilidad a campos magnéticos, experimentos científicos y estudios biomédicos (la interacción entre el campo magnético y el tejido vivo). Los campos magnéticos requeridos suelen ser pulsantes o de onda sinusoidal continua. El rango de frecuencia del campo magnético puede variar desde cerca de CC (0 Hz) hasta muchos kilohercios o incluso megahercios (MHz). Se necesita un controlador de bobina de Helmholtz de CA para generar el campo magnético variable en el tiempo requerido. El controlador del amplificador de forma de onda debe poder generar una corriente alterna alta para producir el campo magnético.

Tensión y corriente del controlador

${displaystyle I=left({frac {5}{4}}right)^{3/2}left({frac {BR}{mu _{0}n}}right)}$

Utilice la ecuación anterior en la sección de matemáticas para calcular la corriente de la bobina para un campo magnético deseado, $B .$

Donde ${displaystyle mu _{0}}$ es la permeabilidad del espacio libre o ${displaystyle 4pi times 10^{-7}{text{ T}}cdot {text{m/A}}=1.257times 10^{-6}{text{ T}}cdot {text{m/A}},}$

${displaystyle I;}$ = corriente de bobina, en amperios,

${displaystyle R;}$ = radio de bobina, en metros,

n = número de vueltas en cada bobina.

Utilizando un generador de función y un controlador amplificador de onda de alta corriente para generar campo magnético Helmholtz de alta frecuencia

Luego calcule el voltaje requerido del amplificador del controlador de bobina de Helmholtz:

{displaystyle V=I{sqrt {{bigl [}omega {bigl (}L_{1}+L_{2}{bigr)}{bigr ]}^{2}+{bigl (}R_{1}+R_{2}{bigr)}^{2}}}}

dónde

$I$ es la corriente pico,
$\cdot$ es la frecuencia angular o $\cdot = 2 πf$ ,
$L 1$ y $L 2$ son las inductancias de las dos bobinas Helmholtz, y
$R 1$ y $R 2$ son las resistencias de las dos bobinas.

Serie resonante de alta frecuencia

Generar un campo magnético estático es relativamente fácil; la fuerza del campo es proporcional a la corriente. Generar un campo magnético de alta frecuencia es más difícil. Las bobinas son inductores, y su impedancia aumenta proporcionalmente con frecuencia. Para proporcionar la misma intensidad de campo al doble de la frecuencia requiere el doble de tensión a través de la bobina. En lugar de conducir directamente la bobina con un alto voltaje, se puede utilizar un circuito resonante de serie para proporcionar el alto voltaje. Un condensador de serie se añade en serie con las bobinas. La capacitancia es elegida para resonar la bobina a la frecuencia deseada. Sólo quedan las bobinas de resistencia parasitaria. Este método sólo funciona en frecuencias cercanas a la frecuencia resonante; para generar el campo en otras frecuencias requiere diferentes capacitores. La frecuencia de resonancia de la bobina Helmholtz, ${displaystyle f_{0}}$ , y el valor capacitor, C, se dan a continuación.

{displaystyle f_{0}={frac {1}{2pi {sqrt {left(L_{1}+L_{2}right)C}}}}}

{displaystyle C={frac {1}{left(2pi f_{0}right)^{2}left(L_{1}+L_{2}right)}}}

Bobinas de Maxwell

Para mejorar la uniformidad del campo en el espacio dentro de las bobinas, se pueden añadir bobinas adicionales alrededor del exterior. James Clerk Maxwell mostró en 1873 que una tercera bobina de mayor diámetro situada a mitad de camino entre las dos bobinas de Helmholtz con la distancia de la bobina aumentó del radio de bobina ${displaystyle R}$ a ${displaystyle {sqrt {3}}R}$ puede reducir la varianza del campo en el eje a cero hasta el sexto derivado de la posición. Esto se llama a veces una bobina Maxwell.

Contenido relacionado

Más resultados...