Bloqueo de cardán

Bloqueo de cardán es la pérdida de un grado de libertad en un mecanismo tridimensional de tres cardanes que ocurre cuando los ejes de dos de los tres cardanes se conducen a una configuración paralela, &# 34;bloqueo" el sistema en rotación en un espacio bidimensional degenerado.

El término cardán-bloqueo puede ser engañoso en el sentido de que ninguno de los cardanes individuales está realmente restringido. Los tres cardanes aún pueden girar libremente sobre sus respectivos ejes de suspensión. Sin embargo, debido a la orientación paralela de dos de los gimbals' ejes no hay cardán disponible para acomodar la rotación alrededor de un eje, dejando el objeto suspendido efectivamente bloqueado (es decir, incapaz de rotar) alrededor de ese eje.

Gimbals

Un cardán es un anillo que está suspendido para que pueda girar sobre un eje. Los cardanes generalmente se anidan uno dentro de otro para adaptarse a la rotación sobre múltiples ejes.

Aparecen en giroscopios y en unidades de medida de inercia para permitir que la orientación del cardán interno permanezca fija mientras que la suspensión del cardán externo asume cualquier orientación. En las brújulas y los mecanismos de almacenamiento de energía del volante de inercia, permiten que los objetos permanezcan en posición vertical. Se utilizan para orientar los propulsores de los cohetes.

Algunos sistemas de coordenadas en matemáticas se comportan como si se usaran cardanes reales para medir los ángulos, especialmente los ángulos de Euler.

Para los casos de tres cardanes anidados o menos, el bloqueo del cardán inevitablemente ocurre en algún punto del sistema debido a las propiedades de los espacios de cobertura.

En ingeniería

Mientras que solo dos orientaciones específicas producen un bloqueo de cardán exacto, los cardanes mecánicos prácticos encuentran dificultades cerca de esas orientaciones. Cuando un conjunto de cardanes está cerca de la configuración bloqueada, las pequeñas rotaciones de la plataforma del cardán requieren grandes movimientos de los cardanes circundantes. Aunque la relación es infinita solo en el punto de bloqueo del cardán, los límites prácticos de velocidad y aceleración de los cardanes, debido a la inercia (resultante de la masa de cada anillo del cardán), la fricción del cojinete, la resistencia al flujo de aire u otro fluido que rodea el los cardanes (si no están en el vacío) y otros factores físicos y de ingeniería limitan el movimiento de la plataforma cerca de ese punto.

En dos dimensiones

El bloqueo de cardán puede ocurrir en sistemas de cardán con dos grados de libertad, como un teodolito con rotaciones sobre un acimut y elevación en dos dimensiones. Estos sistemas pueden bloquear el cardán en el cenit y el nadir, porque en esos puntos el azimut no está bien definido y la rotación en la dirección del azimut no cambia la dirección a la que apunta el teodolito.

Considere el seguimiento de un helicóptero que vuela hacia el teodolito desde el horizonte. El teodolito es un telescopio montado en un trípode para que pueda moverse en azimut y elevación para rastrear el helicóptero. El helicóptero vuela hacia el teodolito y es seguido por el telescopio en elevación y azimut. El helicóptero vuela inmediatamente por encima del trípode (es decir, está en el cenit) cuando cambia de dirección y vuela a 90 grados de su rumbo anterior. El telescopio no puede seguir esta maniobra sin un salto discontinuo en una o ambas orientaciones del cardán. No hay un movimiento continuo que le permita seguir al objetivo. Está en bloqueo de cardán. Entonces, hay una infinidad de direcciones alrededor del cenit para las cuales el telescopio no puede seguir continuamente todos los movimientos de un objetivo. Tenga en cuenta que incluso si el helicóptero no pasa por el cenit, sino solo cerca del cenit, de modo que no se produzca el bloqueo del cardán, el sistema aún debe moverse excepcionalmente rápido para seguirlo, ya que pasa rápidamente de un rumbo al otro. Cuanto más cerca del cenit esté el punto más cercano, más rápido se debe hacer esto, y si realmente pasa por el cenit, el límite de estos "cada vez más rápido" los movimientos se vuelven infinitamente rápidos, es decir, discontinuos.

Para recuperarse del bloqueo del cardán, el usuario tiene que dar la vuelta al cenit, explícitamente: reducir la elevación, cambiar el azimut para que coincida con el azimut del objetivo y luego cambiar la elevación para que coincida con el objetivo.

Matemáticamente, esto corresponde al hecho de que las coordenadas esféricas no definen un gráfico de coordenadas en la esfera en el cenit y el nadir. Alternativamente, el mapa correspondiente T²→S² del toroide T² a la esfera S² (dada por el punto con azimut y elevación dados) no es un mapa de cobertura en estos puntos.

En tres dimensiones

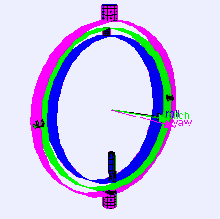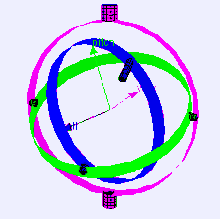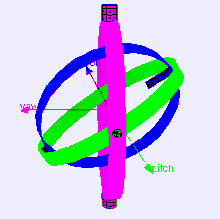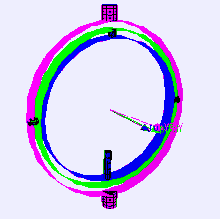
Considere el caso de una plataforma de detección de nivel en un avión que vuela hacia el norte con sus tres ejes cardánicos mutuamente perpendiculares (es decir, ángulos de balanceo, cabeceo y guiñada cada cero). Si la aeronave se inclina hacia arriba 90 grados, el cardán del eje de guiñada de la aeronave y la plataforma se vuelve paralelo al cardán del eje de balanceo, y los cambios en la guiñada ya no se pueden compensar.

Soluciones

Este problema se puede solucionar mediante el uso de un cuarto cardán, accionado activamente por un motor para mantener un gran ángulo entre los ejes del cardán de balanceo y guiñada. Otra solución es girar uno o más cardanes a una posición arbitraria cuando se detecta el bloqueo del cardán y así restablecer el dispositivo.

La práctica moderna es evitar por completo el uso de cardanes. En el contexto de los sistemas de navegación inercial, eso se puede hacer montando los sensores inerciales directamente en la carrocería del vehículo (esto se denomina sistema strapdown) e integrando digitalmente la rotación y la aceleración detectadas utilizando métodos de cuaterniones para derivar la orientación y la velocidad del vehículo. Otra forma de reemplazar cardanes es usar cojinetes de fluido o una cámara de flotación.

En el Apolo 11

Ocurrió un conocido incidente de bloqueo de cardán en la misión lunar del Apolo 11. En esta nave espacial, se utilizó un conjunto de cardanes en una unidad de medida inercial (IMU). Los ingenieros estaban al tanto del problema del bloqueo del cardán, pero se negaron a usar un cuarto cardán. Parte del razonamiento detrás de esta decisión se desprende de la siguiente cita:

Las ventajas de la ginebra redundante parecen estar superadas por la simplicidad del equipo, las ventajas del tamaño y la correspondiente fiabilidad implícita de la unidad directa de tres grados de libertad.

—David Hoag, Apollo Lunar Surface Journal

Prefirieron una solución alternativa usando un indicador que se activaría cuando estuviera cerca de los 85 grados de inclinación.

Cerca de ese punto, en un bucle de estabilización cerrado, los motores de par pueden teóricamente ser ordenados para voltear el gimbal 180 grados instantáneamente. En su lugar, en el LM, el ordenador lanzó una advertencia de "cerradura gigante" a 70 grados y congeló el IMU a 85 grados

—Paul Fjeld, Apollo Lunar Surface Journal

En lugar de intentar impulsar los cardanes más rápido de lo que podían, el sistema simplemente se dio por vencido y congeló la plataforma. Desde este punto, la nave espacial tendría que alejarse manualmente de la posición de bloqueo del cardán y la plataforma tendría que realinearse manualmente usando las estrellas como referencia.

Después de que el Módulo Lunar aterrizara, Mike Collins, a bordo del Módulo de Comando, bromeó: "¿Qué tal si me envías un cuarto cardán para Navidad?".

Robótica

En robótica, el bloqueo de cardán se conoce comúnmente como "giro de muñeca", debido al uso de una "muñeca de triple giro" en brazos robóticos, donde los tres ejes de la muñeca, que controlan la guiñada, el cabeceo y el balanceo, pasan por un punto común.

Un ejemplo de giro de muñeca, también llamado singularidad de muñeca, es cuando la ruta por la que se desplaza el robot hace que el primer y el tercer eje de la muñeca del robot se alineen. El segundo eje de la muñeca luego intenta girar 180° en tiempo cero para mantener la orientación del efector final. El resultado de una singularidad puede ser bastante dramático y puede tener efectos adversos en el brazo del robot, el efector final y el proceso.

La importancia de evitar las singularidades en la robótica ha llevado al Estándar Nacional Estadounidense para Robots Industriales y Sistemas de Robots – Requisitos de Seguridad a definirlo como "una condición causada por la alineación colineal de dos o más ejes del robot que resulta en un robot impredecible movimiento y velocidades".

En matemáticas aplicadas

El problema del bloqueo del cardán aparece cuando se usan ángulos de Euler en matemáticas aplicadas; los desarrolladores de programas informáticos en 3D, como el modelado en 3D, los sistemas de navegación integrados y los videojuegos, deben tener cuidado de evitarlo.

En lenguaje formal, el bloqueo de cardán se produce porque el mapa de Euler se inclina hacia las rotaciones (topológicamente, desde el 3-torus T³ hasta el espacio proyectivo real RP³, que es el mismo que el espacio de rotaciones para cuerpos rígidos tridimensionales, formalmente llamado SO(3)) no es un homeomorfismo local en cada punto y, por lo tanto, en algunos puntos el rango (grados de libertad) debe caer por debajo de 3, momento en el que se produce el bloqueo del cardán. Los ángulos de Euler proporcionan un medio para dar una descripción numérica de cualquier rotación en el espacio tridimensional utilizando tres números, pero no solo esta descripción no es única, sino que hay algunos puntos en los que no se pueden realizar todos los cambios en el espacio objetivo (rotaciones). por un cambio en el espacio fuente (ángulos de Euler). Esta es una restricción topológica: no hay un mapa de cobertura desde el toroide tridimensional hasta el espacio proyectivo real tridimensional; el único mapa de cobertura (no trivial) es de 3 esferas, como en el uso de cuaterniones.

Para hacer una comparación, todas las traducciones se pueden describir utilizando tres números x{displaystyle x}, Sí.{displaystyle y}, y z{displaystyle z}, como la sucesión de tres movimientos lineales consecutivos a lo largo de tres ejes perpendiculares X{displaystyle X}, Y{displaystyle Sí. y Z{displaystyle Z} ejes. Lo mismo es cierto para las rotaciones: todas las rotaciones se pueden describir utilizando tres números α α {displaystyle alpha }, β β {displaystyle beta }, y γ γ {displaystyle gamma }, como la sucesión de tres movimientos rotacionales alrededor de tres ejes perpendiculares uno a otro. Esta similitud entre coordenadas lineales y coordenadas angulares hace que los ángulos de Euler sean muy intuitivos, pero por desgracia sufren del problema de bloqueo gimbal.

Pérdida de un grado de libertad con ángulos de Euler

Una rotación en el espacio 3D se puede representar numéricamente con matrices de varias maneras. Una de estas representaciones es:

R=[1000#⁡ ⁡ α α − − pecado⁡ ⁡ α α 0pecado⁡ ⁡ α α #⁡ ⁡ α α ][#⁡ ⁡ β β 0pecado⁡ ⁡ β β 010− − pecado⁡ ⁡ β β 0#⁡ ⁡ β β ][#⁡ ⁡ γ γ − − pecado⁡ ⁡ γ γ 0pecado⁡ ⁡ γ γ #⁡ ⁡ γ γ 0001]{fnMicrosoft Sans {fnMicrosoft Sans Serif} {fnMicrosoft Sans {cH0cH0ccH0cH0cH0cH0cH00cH00cH00cH00cH00cH00cH00cH0cH00cH0cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH0cH00cH00cH00cH00 {}}

Un ejemplo que vale la pena examinar ocurre cuando β β =π π 2{displaystyle beta ={tfrac ♪ } {2}}. Saber que #⁡ ⁡ π π 2=0{displaystyle cos {tfrac ♪ } {2}=0} y pecado⁡ ⁡ π π 2=1{displaystyle sin {tfrac ♪ } {2}=1}, la expresión anterior se hace igual a:

R=[1000#⁡ ⁡ α α − − pecado⁡ ⁡ α α 0pecado⁡ ⁡ α α #⁡ ⁡ α α ][001010− − 100][#⁡ ⁡ γ γ − − pecado⁡ ⁡ γ γ 0pecado⁡ ⁡ γ γ #⁡ ⁡ γ γ 0001]{displaystyle {begin{aligned}Riéndose={begin{bmatrix}1 coincide0 âTMacos alpha 'sin alpha \0 simultáneamentesin alpha >cos alpha end{bmatrix}{begin{bmatrix}0 ventaja1 rest1\1 recur0end{bmatrix}}{begin{bmatrix}cos gamma &sin gamma &0\\pegamma {}}

Realizando la multiplicación de matrices:

R=[001pecado⁡ ⁡ α α #⁡ ⁡ α α 0− − #⁡ ⁡ α α pecado⁡ ⁡ α α 0][#⁡ ⁡ γ γ − − pecado⁡ ⁡ γ γ 0pecado⁡ ⁡ γ γ #⁡ ⁡ γ γ 0001]=[001pecado⁡ ⁡ α α #⁡ ⁡ γ γ +#⁡ ⁡ α α pecado⁡ ⁡ γ γ − − pecado⁡ ⁡ α α pecado⁡ ⁡ γ γ +#⁡ ⁡ α α #⁡ ⁡ γ γ 0− − #⁡ ⁡ α α #⁡ ⁡ γ γ +pecado⁡ ⁡ α α pecado⁡ ⁡ γ γ #⁡ ⁡ α α pecado⁡ ⁡ γ γ +pecado⁡ ⁡ α α #⁡ ⁡ γ γ 0]{beplaystyle {begin{aligned}Riéndose={begin{bmatrix}0 limitado1\sin alpha &cos alpha &0-cos alpha &sin alpha &0end{bmatrix}{begin{bmatrix}cos gamma >singamma {begin{bmatrix}0 âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa0 âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa â alpha cos gamma +cos alpha sin gamma &sin alpha gamma +cos alpha cos gamma &0\-cos alpha cos gamma +sin alphasin gamma > alpha gamma +sin alpha gaendmma &0end {bmatrix}

Y finalmente usando las fórmulas trigonométricas:

R=[001pecado⁡ ⁡ ()α α +γ γ )#⁡ ⁡ ()α α +γ γ )0− − #⁡ ⁡ ()α α +γ γ )pecado⁡ ⁡ ()α α +γ γ )0]{displaystyle {begin{aligned}Riéndose={begin{bmatrix}0 sensible01\sin(alpha +gamma) implicacos(alpha +gamma) implica0-cos(alpha +gamma)}endal

Cambiar los valores de α α {displaystyle alpha } y γ γ {displaystyle gamma } en la matriz anterior tiene los mismos efectos: el ángulo de rotación α α +γ γ {displaystyle alpha +gamma } cambios, pero el eje de rotación permanece en el Z{displaystyle Z} dirección: la última columna y la primera fila en la matriz no cambiará. La única solución para α α {displaystyle alpha } y γ γ {displaystyle gamma } recuperar diferentes roles es cambiar β β {displaystyle beta }.

Es posible imaginar un avión rotado por los ángulos Euler mencionados anteriormente utilizando los X-Y-Z convención. En este caso, el primer ángulo - α α {displaystyle alpha } es el lanzamiento. Yaw está listo para π π 2{\fnMicroc {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\\fnMicrosoft {\\\fnMicrosoft {\\fnMicrosoft {\\\\\\\fnMicrosoft {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ } {2}} y la rotación final - por γ γ {displaystyle gamma } - es otra vez el lanzamiento del avión. Debido al bloqueo gimbal, ha perdido uno de los grados de libertad - en este caso la capacidad de rodar.

También es posible elegir otra convención para representar una rotación con una matriz usando ángulos de Euler que la convención X-Y-Z anterior, y también elegir otros intervalos de variación para los ángulos, pero al final hay siempre al menos un valor para el que se pierde un grado de libertad.

The gimbal lock problem does not make Euler angles "invalid#34; (they always serve as a well-defined coordinate system), but it makes them suited for some practical applications.

Representación de orientación alternativa

La causa del bloqueo del cardán es la representación de la orientación en los cálculos como tres rotaciones axiales basadas en ángulos de Euler. Por lo tanto, una posible solución es representar la orientación de alguna otra manera. Esto podría ser como una matriz de rotación, un cuaternión (ver cuaterniones y rotación espacial) o una representación de orientación similar que trata la orientación como un valor en lugar de tres valores separados y relacionados. Dada tal representación, el usuario almacena la orientación como un valor. Para cuantificar los cambios angulares producidos por una transformación, el cambio de orientación se expresa como una rotación del eje/ángulo delta. La orientación resultante debe volver a normalizarse para evitar la acumulación de errores de coma flotante en transformaciones sucesivas. Para matrices, volver a normalizar el resultado requiere convertir la matriz en su representación ortonormal más cercana. Para los cuaterniones, la renormalización requiere realizar la normalización de cuaterniones.