Bipirámide hexagonal
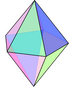
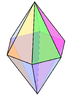
Una bipirámide hexagonal es un poliedro formado por dos pirámides hexagonales unidas por sus bases. El sólido resultante tiene 12 caras triangulares, 8 vértices y 18 aristas. Las 12 caras son triángulos isósceles idénticos.
Aunque es transitivo de caras, no es un sólido platónico porque algunos vértices tienen cuatro caras que se juntan y otros tienen seis caras, y no es un sólido de Johnson porque sus caras no pueden ser triángulos equiláteros; 6 triángulos equiláteros formarían un vértice plano.
Es una de un conjunto infinito de bipirámides. Al tener doce caras, es un tipo de dodecaedro, aunque ese nombre suele asociarse a la forma poliédrica regular de caras pentagonales.
La bipirámide hexagonal tiene un plano de simetría (que es horizontal en la figura de la derecha) donde se unen las bases de las dos pirámides. Este plano es un hexágono regular. También hay seis planos de simetría que atraviesan los dos ápices. Estos planos son rómbicos y forman ángulos de 30° entre sí, perpendiculares al plano horizontal.
Imágenes
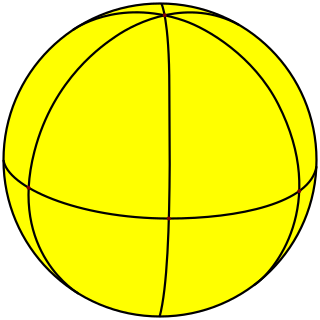
Se puede dibujar como un mosaico sobre una esfera que también representa los dominios fundamentales de la simetría diédrica [3,2], *322:
Poliedros relacionados
La bipirámide hexagonal, dt{2,6}, puede estar en secuencia truncada, tdt{2,6} y alternada (desairada), sdt{2,6}:
La bipirámide hexagonal, dt{2,6}, puede ser en secuencia rectificada, rdt{2,6}, truncada, trdt{2,6} y alternada (desairada), srdt{ 2,6}:
| Uniform hexagonal dihedral spherical polyhedra | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Simetría: [6,2], (*622) | [6,2]+, (622) | [6,2]+], (2*3) | ||||||||||||
 |  | |  |  |  |  |  |  | ||||||
    | | | | | | |   | | ||||||
| {6,2} | t{6,2} | r{6,2} | t{2,6} | {2,6} | rr{6,2} | tr{6,2} | sr{6,2} | S{2,6} | ||||||
| Duals to uniforms | ||||||||||||||
|  | |  | | |  |  |  | ||||||
| V62 | V122 | V62 | V4.4.6 | V26 | V4.4.6 | V4.4.12 | V3.3.3.6 | V3.3.3.3 | ||||||
Es el primer polihedra en una secuencia definida por la configuración facial V4.6.2n. Este grupo es especial para tener todo el número de bordes por vértice y formar planos de bisección a través de la polihedra y líneas infinitas en el plano, y continuar en el plano hiperbólico para cualquier n≥ ≥ 7.{displaystyle ngeq 7.}
Con un número par de caras en cada vértice, estos poliedros y mosaicos se pueden mostrar alternando dos colores para que todas las caras adyacentes tengan colores diferentes.
Cada cara en estos dominios también corresponde al dominio fundamental de un grupo de simetría con espejos de orden 2,3,n en cada vértice de la cara del triángulo.
| *n32 mutación de simetría de los revestimientos omnímicos: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n32 [n,3] | Spherical | Euclid. | Hiperb compacto. | Paraco. | Hiperbólico no consumado | |||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3] | *∞32 [∞,3] | [12i,3] | [9i,3] | [6i,3] | [3i,3] | |
| Gráficos | |  |  |  |  |  |  |  |  |  |  |  |
| Config. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6. | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duales | |  |  |  |  |  |  |  |  |  |  |  |
| Config. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6. | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
| Bipyramid Nombre | Digonal bipyramid | Bipyramid triangular | Bipyramid cuadrado | Bipirámide pentagonal | Bipirámide hexagonal | ... | Bipyramid Apeirogonal |
|---|---|---|---|---|---|---|---|
| Polyhedron imagen |  |  |  |  | ... | ||
| Tilo esférico imagen |  |  |  |  |  | Planeamiento imagen |  |
| Config facial. | V2.4.4 | V3.4.4 | V4.4.4 | V5.4.4 | V6.4.4 | ... | V dieta.4.4 |
| Coxeter diagrama |  |  |  |  | | ... |  |