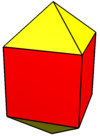
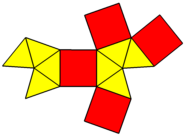
Bipirámide cuadrada alargada

En geometría, la bipirámide cuadrada alargada (u octaedro alargado) es uno de los sólidos de Johnson (J₁₅). Como sugiere el nombre, se puede construir alargando un octaedro insertando un cubo entre sus mitades congruentes. También se puede ver como 4 lunes (cuadrados con triángulos en lados opuestos) unidos entre sí con cuadrados con cuadrados y triángulos con triángulos.

Se le ha llamado cubo de lápiz o cubo de lápiz de 12 caras debido a su forma.

Un sólido de Johnson es uno de los 92 poliedros estrictamente convexos que se componen de caras de polígonos regulares pero que no son poliedros uniformes (es decir, no son sólidos platónicos, sólidos de Arquímedes, prismas o antiprismas). Fueron nombrados por Norman Johnson, quien enumeró estos poliedros por primera vez en 1966.

Un cristal de circón es un ejemplo de bipirámide cuadrada alargada.

Fórmulas

Las siguientes fórmulas para el volumen (${\displaystyle V}$), superficie (${\displaystyle A}$) y altura (${\displaystyle H.$) se puede utilizar si todas las caras son regulares, con longitud de borde ${\displaystyle L.$:

${\displaystyle V=L^{3}\cdot \left(1+{\frac {\sqrt {2}{3}\right)\approx L^{3}\cdot 1.471404521}$

${\displaystyle A=L^{2}\cdot \left(4+2{\sqrt {3}\right)\approx L^{2}\cdot 7.464101615}$

${\displaystyle H=L\cdot \left(1+{\sqrt {2}\right)\approx L\cdot 2.414213562}$

Poliedro dual

El dual de la bipirámide cuadrada alargada se llama bifrustum cuadrado y tiene 10 caras: 8 trapezoidales y 2 cuadradas.

Bipyramid cuadrado alargado	Net of dual

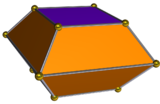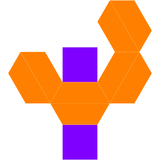Poliedros y panales relacionados

Un tipo especial de bipirámide cuadrada alargada sin todas las caras regulares permite una autoteselación del espacio euclidiano. Los triángulos de esta bipirámide cuadrada alargada no son regulares; tienen bordes en la proporción 2:√3:√3.

Se puede considerar una fase de transición entre los panales dodecaédricos cúbicos y rómbicos. Aquí las celdas están coloreadas de blanco, rojo y azul según su orientación en el espacio. Las tapas de las pirámides cuadradas tienen caras de triángulos isósceles acortadas, y seis de estas pirámides se unen para formar un cubo. El dual de este panal se compone de dos tipos de octaedros (octaedros regulares y antiprismas triangulares), formados por la superposición de octaedros en los cuboctaedros del panal cúbico rectificado. Ambos panales tienen una simetría de [[4,3,4]].

Las secciones transversales del panal, a través de los centros de las celdas, producen un mosaico cuadrado achaflanado, con hexágonos horizontales y verticales aplanados, y cuadrados en los poliedros perpendiculares.

Honeycomb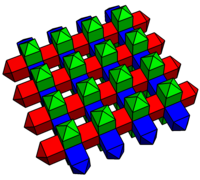

Medio panalb

Tejas cuadradas

Con caras regulares, la bipirámide cuadrada alargada puede formar un mosaico de espacio con tetraedros y octaedros. (Los octaedros se pueden descomponer aún más en pirámides cuadradas). Este panal puede considerarse una versión alargada del panal tetraédrico-octaédrico.