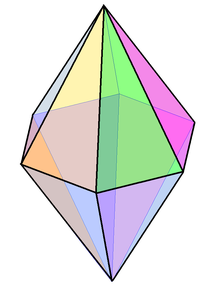
Bipirámide

Conjunto de doble-uniform n- bipirámides pasadas
Ejemplo: dual-uniform bipirámide hexagonaln = 6)
Tipo	dual-uniform en el sentido de poliedro semiregular dual-semiregular
Coxeter diagrama
Símbolo Schläfli	{} + {}n}
Caras	2n triángulos isosceles congruentes
Edges	3n
Vertices	2 + n
Configuración facial	V4.4.n
Grupo de Symmetry	Dnh, [n,2], (*n22), orden 4n
Grupo de rotación	Dn, [n,2]+, (n22), orden 2n
Poliedro dual	(convex) el prisma n-gonal uniforme
Propiedades	convex, cara-transitiva, vertices regulares
Cifras netas	Ejemplo: red de bipirámide pentagonal (n = 5)

A (simétrica) n-gonal bipirámide o dipirámide es un poliedro formado al unir una pirámide n-gonal y su imagen especular de base a base. Una bipirámide n-gonal tiene 2n caras triangulares, 3n aristas y 2 + n vértices.

La "n-gonal" en el nombre de una bipirámide no se refiere a una cara sino a la base del polígono interno, que se encuentra en el plano del espejo que conecta las dos mitades de la pirámide. (Si fuera una cara, cada uno de sus bordes conectaría tres caras en lugar de dos).

"Regular", bipirámides derechas

Una "regular" bipirámide tiene una base poligonal regular. Por lo general, se da a entender que también es una bipirámide derecha.

Una bipirámide derecha tiene sus dos vértices derecha arriba y derecha debajo del centro o del baricentro de la base de su polígono.

Un "regular" derecha (simétrica) bipirámide n-gonal tiene el símbolo de Schläfli { } + {n}.

Una bipirámide derecha (simétrica) tiene el símbolo de Schläfli { } + P, para la base del polígono P.

El "regular" la bipirámide n-gonal con vértices regulares es la dual de la n-prisma uniforme gonal (por lo tanto a la derecha), y tiene caras triangulares isósceles congruentes.

Un "regular" derecha (simétrica) la bipirámide n-gonal se puede proyectar en una esfera o globo como un "regular" derecha (simétrica) n-gonal bipirámide esférica: n líneas de longitud igualmente espaciadas que van de polo a polo, y una línea ecuatorial que las biseca.

"Regular" derecha (simétrica) n- bipirámides pasadas:

Nombre bipyramid	Bipyramid digonal	Bipirámide triangular (Véase: J12)	Bipyramid cuadrado (Véase: O)	Bipirámide pentagonal (Véase: J13)	Bipirámide hexagonal	Bipirámide heptagonal	Bipirámide octogonal	Bipyramid enneagonal	Bipyramid Decagonal	...	Bipyramid Apeirogonal
Imagen de poliedro										...
Imagen de revestimiento esférico										Imagen de azulado plano
Config facial.	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...	V dieta.4.4
Coxeter diagrama										...

Bipirámides de triángulos equiláteros

Solo tres tipos de bipirámides pueden tener todas las aristas de la misma longitud (lo que implica que todas las caras son triángulos equiláteros y, por lo tanto, la bipirámide es un deltaedro): la "regular" bipirámides rectas (simétricas) triangulares, tetragonales y pentagonales. La bipirámide tetragonal o cuadrada con aristas de igual longitud, u octaedro regular, cuenta entre los sólidos platónicos; las bipirámides triangulares y pentagonales con aristas de la misma longitud cuentan entre los sólidos de Johnson (J₁₂ y J₁₃ ).

Bipirámides triángulo equilátero:

"Regular" derecha (simétrica) nombre bipyramid	Bipirámid Trigonal o Triangular J12	Bipirámide Tetragonal o cuadrado (Octaedro regional) O	Bipirámide pentagonal J13
Imagen bipyramid

Simetría caleidoscópica

Un "regular" derecho (simétrico) n-bipirámide bigonal tiene grupo de simetría diédrica D_nh, de orden 4n, excepto en el caso de un regular octaedro, que tiene el grupo de simetría octaédrica más grande O_h, de orden 48, que tiene tres versiones de D_4h como subgrupos. El grupo de rotación es D_n, de orden 2n, excepto en el caso de un octaedro regular, que tiene el grupo de rotación mayor O, de orden 24, que tiene tres versiones de D₄ como subgrupos.

Nota: Cada "regular" la bipirámide derecha (simétrica) n-gonal tiene el mismo grupo de simetría (diédrica) que el uniforme dual n-bipirámide bigonal, para n ≠ 4.

Las 4n caras triangulares de un "regular" derecha (simétrica) 2n-gonal bipirámide, proyectada como la 4n caras triangulares esféricas de un "regular" derecha (simétrica) 2n-gonal esférica bipirámide, representan los dominios fundamentales de simetría diédrica en tres dimensiones: D_nh, [n,2], (*n22), de orden 4 n. Estos dominios se pueden mostrar como triángulos esféricos de colores alternativos:

• a través de un plano de reflexión a través de bordes cocíclicos, dominios de imagen espejo están en diferentes colores (isometría indirecta);
• sobre una n- el doble o el 2- eje de rotación múltiple a través de vértices opuestos, un dominio y su imagen están en el mismo color (isometría directa).

Una bipirámide n-gonal (simétrica) puede verse como el Kleetope de la "correspondiente" Diedro n-gonal.

Dominios fundamentales de simetría dihedral en tres dimensiones:

Simmetría Dihedral	D1h	D2h	D3h	D4h	D5h	D6h	...	Dnh
Imagen de dominios fundamentales							...
Coxeter diagrama							...

Volumen

Volumen de una bipirámide (simétrica):

V=23Bh,{displaystyle V={frac {2}}Bh,}

Esto funciona para cualquier forma de la base y para cualquier ubicación de los ápices, siempre que h se mida como la distancia perpendicular desde el plano base a cualquier vértice. Por eso:

Volumen de una bipirámide (simétrica) cuya base es un polígono regular n lados con longitud del lado s y cuya altura es h :

V=n6hs2cot⁡ ⁡ π π n.{displaystyle V={frac {fn}}hs^{2}cot {fnfn} {fn} {fn} {fn} {fn} {fn} {fn}} {fn} {fn} {fn} {fn}}hs}hs} {fn} {fn} {f}f}f}}}}}}}}hs}f}hs}hs}hs}hs}hs} {f} {f}f}f}hs}hs}f} {fn}f}f}f}f}f}f}f}fn}f}fn}f}fn}f}f}f}fn}f}f}f}fn}fn}fn}fn}f}fn}f}fn}f}f}f } {n}}

Oblique bipyramids

Las bipirámides no derechas se denominan bipirámides oblicuas.

Bipirámides cóncavas

Una bipirámide cóncava tiene una base poligonal cóncava.

Ejemplo: cóncava (simétrica) bipirámide tetragonal (n = 4) (*)

(*) Su base no tiene un centro evidente; pero si sus vértices están derecho arriba y derecho debajo del centroide de su base, entonces es una bipirámide derecha. De todos modos, es un octaedro cóncavo.

Bipirámides derechas asimétricas/invertidas

Una bipirámide derecha asimétrica une dos pirámides derechas con bases congruentes pero alturas desiguales, de base a base.

Una bipirámide derecha invertida une dos pirámides derechas con bases congruentes pero alturas desiguales, base con base, pero del mismo lado de su base común.

El dual de una bipirámide n-gonal asimétrica/invertida es un n-truncado gonal.

Un "regular" n-bipirámide bigonal asimétrica/invertida tiene un grupo de simetría C_{n v}, de orden 2n.

Ejemplos: bipirámides hexagonales derecha "regulares" asimétricas/invertidas (n = 6):

Asimétrica	Invertidos

Bipirámides del triángulo escaleno

Ejemplo: bipirámide ditetragonal2n = 2×4)

Un "isotoxal" derecha (simétrica) di-n-gonal bipirámide es una bipirámide derecha (simétrica) 2n-gonal con una Base poligonal plana isotoxal: sus 2n vértices basales son coplanares, pero se alternan en dos radios.

Todas sus caras son triángulos escalenos congruentes y es isoédrico. Puede verse como otro tipo de derecho "simétrico" escalenoedro di-n-gonal, con base de polígono plano isotoxal.

Un "isotoxal" derecha (simétrica) bipirámide di-n-gonal tiene n ejes de rotación dobles a través de vértices basales opuestos, n planos de reflexión a través de bordes apicales opuestos, un Eje de rotación n-fold a través de los ápices, un plano de reflexión a través de la base y un n-plegar el eje de rotación-reflexión a través de los ápices, representando el grupo de simetría D_nh, [n,2], (*22n), de orden 4n . (La reflexión sobre el plano base corresponde a la reflexión-rotación 0°. Si n es par, entonces hay una simetría de inversión sobre el centro, correspondiente a la rotación-reflexión 180°).

Ejemplo con 2n = 2×3:

Una bipirámide "isotoxal" derecha (simétrica) ditrigonal tiene tres planos verticales similares de simetría, intersectando en una (vertical) 3- eje de rotación múltiple; perpendicular a ellos es un cuarto plano de simetría (horizontal); en la intersección de los tres planos verticales con el plano horizontal son tres similares (horizontal) 2- ejes de rotación múltiple; no hay centro de simetría de inversión, pero hay un centro de simetría: el punto de intersección de los cuatro ejes.

Ejemplo con 2n = 2×4:

Una bipirámide ditetragonal "isotoxal" derecha (simétrica) tiene cuatro planos verticales de simetría de dos tipos, intersectando en una (vertical) 4- eje de rotación múltiple; perpendicular a ellos es un quinto plano de simetría (horizontal); en la intersección de los cuatro planos verticales con el plano horizontal son cuatro (horizontal) 2- ejes de rotación múltiple de dos tipos, cada perpendicular a un plano de simetría; dos planos verticales bisecan los ángulos entre dos ejes horizontales; y hay un centro de simetría de inversión.

Nota: como máximo para dos valores particulares de z_A = |z_A'|, las caras de tal bipirámide triangular escaleno pueden ser isósceles.

Ejemplo doble:

• La bipirámide con isotoxal 2×2- vértices base:

U = (1,0,0), U = 1,0,0), V = 0,2,0), V = (0,−2,0),

y con apices simétricos "derecha":

A = (0,0,1), A = (0,0,1),

tiene sus caras isosceles. De hecho:

longitudes de borde apical superior:

AU = AU = 2,{displaystyle {sqrt {2}}

AV = AV = 5;{displaystyle {sqrt {5}}}

Longitud del borde base:

UV = VU = U′V = V′ = 5;{displaystyle {sqrt {5}}}

longitudes inferiores de los bordes apicales = arriba.

• La bipirámide con los mismos vértices base, pero con apices simétricos "derecha":

A = (0,0,2), A = (0,0,2),

también tiene sus rostros isosceles. De hecho:

longitudes de borde apical superior:

AU = AU = 5,{displaystyle {sqrt {}}}

AV = AV = 22;{displaystyle {sqrt {2}}

longitud de borde base = anterior = 5;{displaystyle {sqrt {5}}}

longitudes inferiores de los bordes apicales = arriba.

En cristalografía, "isotoxal" derecho (simétrico) "didigonal" (*) (8 caras), ditrigonal (12 caras), ditetragonal ( 16 caras) y bipirámides dihexagonales (24 caras) existen.

Ejemplos de bipirámides rhombic

(*) Las bipirámides geométricas di-n-gonales más pequeñas tienen ocho caras y son topológicamente idénticas al octaedro regular. En este caso (2n = 2×2):
un "isotoxal" derecho (simétrico) "didigonal" bipirámide se llama bipirámide rómbica, aunque todas sus caras son triángulos escalenos, porque su base poligonal plana es un rombo.

Escalenoedros

Ejemplo: báscula ditrigonal (escaldo)2n = 2×3)

Un "regular" derecho "simétrico" di-n-gonal escalenoedro está definido por una base regular 2n-gon en zigzag, dos simétricos ápices derecha arriba y derecha debajo del centro de la base, y caras triangulares que conectan cada borde basal con cada vértice.

Tiene dos ápices y 2n vértices basales, 4n caras y 6n aristas; es topológicamente idéntica a una bipirámide 2n-gonal, pero su 2n los vértices basales se alternan en dos anillos por encima y por debajo del centro.

Todas sus caras son triángulos escalenos congruentes y es isoédrico. Puede verse como otro tipo de derecho "simétrico" Bipirámide di-n-gonal, con una base de polígono regular oblicua en zigzag.

Un "regular" derecho "simétrico" el escalenoedro di-n-gonal tiene n ejes de rotación dobles a través de los bordes medios basales opuestos, n planos de reflexión a través de los bordes apicales opuestos, un n-eje de rotación de pliegues a través de los ápices, y un 2 n-plegar el eje de rotación-reflexión a través de los ápices (sobre los cuales 1n rotaciones- las reflexiones preservan globalmente el sólido), representando el grupo de simetría D_nv = D_nd, [2⁺,2n], (2*n), de orden 4n. (Si n es impar, entonces hay una simetría de inversión sobre el centro, correspondiente a 180° rotación-reflexión.)

Ejemplo con 2n = 2×3:

Un escama ditrigonal "regular" derecho "simétrico" tiene tres planos verticales similares de simetría inclinados unos a otros 60° e intersección en un (vertical) 3- eje de rotación múltiple, tres horizontales similares 2- ejes de rotación múltiple, cada perpendicular a un plano de simetría, un centro de simetría de inversión, y una vertical 6- eje de reflexión de rotación.

Ejemplo con 2n = 2×2:

Un escalanoedro "regular" derecho "simétrico" "didigonal" tiene sólo una vertical y dos horizontales 2- ejes de rotación dobles, dos planos verticales de simetría, que bisectan los ángulos entre el par horizontal de ejes, y un vertical 4- eje de rotación-reflexión múltiple; no tiene centro de simetría de inversión.

Ejemplos de defenoides y de un 8- faced scalenohedron

Nota: como máximo para dos valores particulares de z_A = |z_A'|, las caras de tal edro escaleno pueden ser isósceles.

Ejemplo doble:

• El escronoedro con zigzag regular 2×2- vértices base:

U = (3,0,2), U ' = (−3,0,2), V = (0,3,-2), V ' = (0,−3,2),

y con apices simétricos "derecha":

A = (0,0,3), A ' = (0,0,3),

tiene sus caras isosceles. De hecho:

longitudes de borde apical superior:

AU = AU' = 10,{displaystyle {sqrt {}}}

AV = AV' = 34;{displaystyle {sqrt {34}}}

Longitud del borde base:

UV = VU = U'V' = V'U = 34;{displaystyle {sqrt {34}}}

longitudes inferiores de los bordes apicales = Las superiores.

• El escronoedro con los mismos vértices base, pero con apices simétricos "derecha":

A = 0,0,7), A ' = (0,0,7),

también tiene sus rostros isosceles. De hecho:

longitudes de borde apical superior:

AU = AU' = 34,{displaystyle {sqrt {34}}

AV = AV' = 310;{displaystyle {sqrt {}}}

longitud de borde base = anterior = 34;{displaystyle {sqrt {34}}}

longitudes inferiores de los bordes apicales = Las superiores.

En cristalografía, "regular" derecho "simétrico" "digonal" (8 caras) y ditrigonales (12 caras) existen escalenoedros.

Los escalenoedros geométricos más pequeños tienen ocho caras y son topológicamente idénticos al octaedro regular. En este caso (2n = 2×2), en cristalografía, un "regular" derecho "simétrico" "digonal" El escalenoedro de 8 caras se llama escalenoedro tetragonal.

Enfoquémonos temporalmente en el "regular" derecho "simétrico" Escalenoedros de 8 caras con h = r, es decir, z_A = |z_A'| = x_U = |x_U'| = y_V = |y_V'|. Sus dos vértices se pueden representar como A = (0,0,1), A' = (0,0,− 1), y sus cuatro vértices basales como U = (1,0,z), U&# 39; = (−1,0,z), V = (0,1,−z), V' = (0,−1,−z), donde z es un parámetro entre 0 y 1.
En z = 0, es un octaedro regular; en z = 1, tiene cuatro pares de caras coplanares, y fusionarlas en cuatro triángulos isósceles congruentes lo convierte en un disfenoide; para z > 1, es cóncavo.

Ejemplo: variaciones geométricas con "regular" derecha "simétrica" 8-Besnohedra cara:

z = 0,1	z = 0,25 dólares	z = 0,5	z = 0,95	z = 1,5

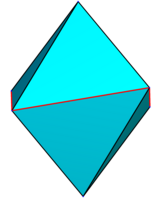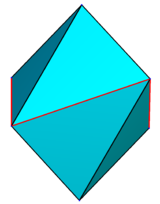Nota: si la base 2n-gon es isotoxal in-out y zigzag sesgada, entonces no todas las caras del "isotoxal" derecho "simétrico" escalenoedro son congruentes.

Ejemplo con cinco longitudes de borde diferentes:

El escronoedro con el skew isotoxal en zigzag 2×2- vértices base:

U = (1,0,1), U = (−1,0,1), V = (0,2,−1), V = (0,−2,1),

y con apices simétricos "derecha":

A = (0,0,3), A = (0,0,3),

tiene caras superiores escalinatas congruentes, y caras inferiores congruentes, pero no todas sus caras son congruentes. De hecho:

longitudes de borde apical superior:

AU = AU = 5,{displaystyle {sqrt {}}}

AV = AV = 25;{displaystyle {sqrt {5}}}

Longitud del borde base:

UV = VU = U′V = V′ = 3;

longitudes inferiores de los bordes apicales:

A′U = A′U = 17,{displaystyle {sqrt {17}}

A′V = A′V = 22.{displaystyle {sqrt {2}}

Nota: para algunos valores particulares de z_A = |z_A'|, la mitad de las caras de tal edro escaleno pueden ser isósceles o equilátero.

Ejemplo con tres longitudes de borde diferentes:

El escronoedro con el skew isotoxal en zigzag 2×2- vértices base:

U = (3,0,2), U ' = (−3,0,2), V = (0,65{displaystyle {sqrt {65}}, - 2), V ' = (0,−65{displaystyle {sqrt {65}}, - 2),

y con apices simétricos "derecha":

A = 0,0,7), A ' = (0,0,7),

tiene caras superiores escamas congruentes, y rostros inferiores equiláteros congruentes; por lo tanto no todas sus caras son congruentes. De hecho:

longitudes de borde apical superior:

AU = AU' = 34,{displaystyle {sqrt {34}}

AV = AV' = 146;{displaystyle {sqrt {146}}

Longitud del borde base:

UV = VU = U'V' = V'U = 310;{displaystyle {sqrt {}}}

longitud del borde apical inferior:

A'U = A'U = 310,{displaystyle {sqrt {}}}

A'V = A'V = 310.{displaystyle {sqrt {}}

"Normal" bipirámides estrella

Una bipirámide de estrella que se corta a sí misma o tiene una base de polígono de estrella.

Un "regular" bipirámide estrella simétrica derecha está definida por una base de polígono estrella regular, dos ápices simétricos derecha arriba y derecha debajo del centro de la base y, por lo tanto, caras triangulares simétricas uno a uno que conectan cada borde basal con cada vértice.

A y#34;normal " la bipirámide estrella simétrica derecha tiene caras triangulares isósceles congruentes y es icosaédrica.

Nota: como máximo para un valor particular de z_A = |z_A'|, las caras de un "regular" la bipirámide estrella puede ser equilátera.

A p/q-bipyramid tiene el diagrama de Coxeter .

Ejemplos de bipirámides de estrella simétrica derecha "regular":

Base de polígono estrella	5/2-gon	7/2-gon	7/3-gon	8/3-gon	9/2-gon	9/4-gon
Imagen bipyramid estrella
Coxeter diagrama

Ejemplos de bipirámides de estrella simétrica derecha "regular":

Base de polígono estrella	10/3-gon	11/2-gon	11/3-gon	11/4-gon	11/5-gon	12/5-gon
Imagen bipyramid estrella
Coxeter diagrama

Bipirámides estrella triángulo escaleno

Un "isotoxal" simétrica derecha 2p/q-gonal estrella bipirámide está definida por una estrella 2p/q-gon base, dos ápices simétricos derecho arriba y derecho debajo del centro de la base, y, por lo tanto, caras triangulares simétricas uno a uno que conectan cada borde basal con cada vértice.

Un "isotoxal" La bipirámide estrella simétrica derecha 2p/q-gonal tiene caras triangulares escalenas congruentes y es isoédrica. Se puede ver como otro tipo de una 2p/q-gonal derecha "simétrica" escalenoedro estelar, con base isotoxal de polígono estelar in-out.

Nota: como máximo para dos valores particulares de z_A = |z_A'|, las caras de tal bipirámide de estrella triangular escaleno pueden ser isósceles.

Ejemplo de un simétrico derecho "isotoxal" 2p/q- la bipirámide estrella pasada:

Base de polígono estrella	Isotoxal in-out 8/3-gon
Imagen bipyramid del triángulo de escalene

Escalenoedros estelares

Un "regular" derecho "simétrico" 2p/q La estrella escalenoedro -gonal está definida por una estrella 2p/q-gon base, dos ápices simétricos derecha arriba y derecha debajo del centro de la base, y caras triangulares que conectan cada borde basal con cada vértice.

Un "regular" derecho "simétrico" El escalenoedro estrella 2p/q-gonal tiene caras triangulares escalenas congruentes y es isoédrico. Puede verse como otro tipo de derecho "simétrico" Bipirámide de estrella 2p/q-gonales, con una base de polígono de estrella oblicua en zigzag regular.

Nota: como máximo para dos valores particulares de z_A = |z_A'|, las caras de tal estrella escalenoedro pueden ser isósceles.

Ejemplo de un "simétrico" derecho "regular" 2p/q- escalofedro estrella:

Base de polígono estrella	Skew 8/3-gon
Imagen de escalinato

Nota: si la base de la estrella 2p/q-gon es isotoxal de entrada y salida y se inclina en zigzag, entonces no todas las caras del "isotoxal" derecho "simétrico" el escalenoedro estelar son congruentes.

Ejemplo de un "isotoxal" derecho "simétrico" 2p/q- escalofedro estrella:

Base de polígono estrella	Isotoxal in-out zigzag skew 8/3-gon
Imagen de escalinato

Nota: para algunos valores particulares de z_A = |z_A'|, la mitad de las caras de tal edro escaleno estelar pueden ser isósceles o equiláteros.

Ejemplo con cuatro longitudes de borde diferentes:

El escronoedro estrella con skew isotoxal in-out 8/3- vértices base:

U₀ = (1,0,1), U₁ = (0,1,1), U₂ = (−1,0,1), U₃ = (0,−1,1),

V₀ = (2,2,−1), V₁ = (−2,−1), V₂ = (2 - 2, - 2,1), V₃ = (2,−2,−1),

y con apices simétricos "derecha":

A = (0,0,3), A = (0,0,3),

tiene caras superiores escalinatas congruentes, y caras inferiores congruentes isosceles; así no todas sus caras son congruentes. De hecho:

longitudes de borde apical superior:

AU₀ = AU₁ = AU₂ = AU₃ = 5,{displaystyle {sqrt {}}}

AV₀ = AV₁ = AV₂ = AV₃ = 26;{displaystyle {sqrt {6}}}

Longitud del borde base:

U₀V₁ = V₁U₃ = U₃V₀ = V₀U₂ = U₂V₃ = V₃U₁ = U₁V₂ = V₂U₀ = 17;{displaystyle {sqrt {17}}

longitudes inferiores de los bordes apicales:

A′U₀ = A′U₁ = A′U₂ = A′U₃ = 17,{displaystyle {sqrt {17}}

A"V₀ = A"V₁ = A"V₂ = A"V₃ = 23.{displaystyle {sqrt {3}}

Ejemplo con tres longitudes de borde diferentes:

El escronoedro estrella con skew isotoxal in-out 8/3- vértices base:

U₀ = (4,0,2{displaystyle {sqrt {2}}), U₁ = 0,42{displaystyle {sqrt {2}}), U₂ = (4,0)2{displaystyle {sqrt {2}}), U₃ = 0, 4,2{displaystyle {sqrt {2}}),

V₀ (6,6, a)2{displaystyle {sqrt {2}}), V₁ = 6 - 62{displaystyle {sqrt {2}}), V₂ (6) – –6,2{displaystyle {sqrt {2}}), V₃ = (6,−6)2{displaystyle {sqrt {2}}),

y con apices simétricos "derecha":

A = 0,0,72{displaystyle {sqrt {2}}), A ' = 0,0−72{displaystyle {sqrt {2}}),

tiene caras superiores escamas congruentes, y rostros inferiores equiláteros congruentes; por lo tanto no todas sus caras son congruentes. De hecho:

longitudes de borde apical superior:

AU₀ = AU₁ = AU₂ = AU₃ = 222,{displaystyle {sqrt {22}}

AV₀ = AV₁ = AV₂ = AV₃ = 102;{displaystyle {sqrt {2}}

Longitud del borde base:

U₀V₁ = V₁U₃ = U₃V₀ = V₀U₂ = U₂V₃ = V₃U₁ = U₁V₂ = V₂U₀ = 12;

longitud del borde apical inferior:

A'U₀ = A'U₁ = A'U₂ = A'U₃ = 12,

A'V₀ = A'V₁ = A'V₂ = A'V₃ = 12.

4-politopos con células bipiramidales

El dual de la rectificación de cada 4 politopos regulares convexos es un 4 politopos transitivos de células con células bipiramidales. A continuación, el vértice del vértice de la bipirámide es A y un vértice del ecuador es E. La distancia entre vértices adyacentes en el ecuador EE = 1, el vértice al borde del ecuador es AE y la distancia entre los vértices es AA. El 4-politopo bipirámide tendrá vértices V_A donde se encuentran los vértices de las bipirámides N_A. Tendrá vértices V_E donde se encuentran los vértices tipo E de las bipirámides N_E. Las bipirámides N_AE se encuentran a lo largo de cada borde tipo AE. Las bipirámides N_EE se encuentran a lo largo de cada borde tipo EE. C_AE es el coseno del ángulo diedro a lo largo de un borde AE. C_EE es el coseno del ángulo diedro a lo largo de un borde EE. Como las celdas deben caber alrededor de un borde, N_EE cos⁻¹(C_EE) ≤ 2π, N_AE cos⁻¹(C_AE) ≤ 2π.

4-polytopes con células bipirámidales

4 propiedades de politopo									Propiedades bipyramid
Dual of	Coxeterdiagram	Celdas	VA	VE	NA	NE	NAE	NEE	Celular	Coxeter diagrama	AA	AE**	CAE	CEE
Rectificado 5 celdas		10	5	5	4	6	3	3	Bipirámide triangular		23{textstyle {frac {2}{3}}	0.667	− − 17{textstyle -{frac {1}{7}}	− − 17{textstyle -{frac {1}{7}}
Tesseract rectificado		32	16	8	4	12	3	4	Bipirámide triangular		23{textstyle {frac {cHFF} {2}{3}} {}} {}}} {}}}}} {}}} {}}}}} {}}} {}}}} {}}}}}} {}}}}} {}}} {}}}}}} {}}}}} {}}}}}} {}}}}}} {}}}}}} {}}}}}}} {}}}}}}}}}} {}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}}} {}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}	0.624	− − 25{textstyle -{frac {2}{5}}	− − 15{textstyle -{frac {1}{5}}
Rectificado 24 celdas		96	24	24	8	12	4	3	Bipirámide triangular		223{textstyle {frac {2{sqrt {2}} {3}}} {}}} {}}} {}}}}} {}}}} {}}}} {}}}} {}}}} {}}}}}}} {}}} {}}}}}}}} {}}}} {}}}}}} {}}}}} {}}}}}}} {}}}} {}}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}} {}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}} {} {}}}}}} {}}}}} {}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}	0,7545	111{textstyle {frac {1}{11}}	− − 511{textstyle -{frac {5}{11}}
Rectificado 120 celdas		1200	600	120	4	30	3	5	Bipirámide triangular		5− − 13{textstyle {frac {cHFF} {5}}} {3}} {}} {}}} {}}} {}}}}} {}}} {}}}} {}}}} {}}}}} {}}}}} {}}}}} {}}}}}} {}}}}}} {}}}}}} {}}}}} {}}}}}} {}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}	0.613	− − 10+9561{textstyle -{frac {10+9{sqrt {}} {61}}} {}}} {}}} {}}}}} {}}}} {}}}} {}}}} {}}} {}}}}}} {}}}} {}}}} {}}}}} {}}}}}} {}}}}} {}}}}}}}}}}}}} {}}}}}}} {}}}}}}}} {}}}} {}}}}}}}} {}}}}}}} {}}}}}}}}}}}} {}}}}} {}}}}} {}}}}}}} {}}}}}} {}}}}}}}}} {} {}}}} {}}}}}} {}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}	− − 7− − 12561{textstyle -{frac {7-12{sqrt {}} {61}}} {}}} {}}} {}}}}} {}}}} {}}}} {}}}} {}}} {}}}}}} {}}}} {}}}} {}}}}} {}}}}}} {}}}}} {}}}}}}}}}}}}} {}}}}}}} {}}}}}}}} {}}}} {}}}}}}}} {}}}}}}} {}}}}}}}}}}}} {}}}}} {}}}}} {}}}}}}} {}}}}}} {}}}}}}}}} {} {}}}} {}}}}}} {}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}
Rectificado 16 celdas		24*	8	16	6	6	3	3	Bipyramid cuadrado		2{fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {cHFF}fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft}\fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft}\fnMicrosoft}\\\\\fnMicrom}\\\fnMicrom}\\\fnMicrom}\\\\\\\\\\\\\\\\\fnMicrom\\fnMicrom\fnMicrosoft\\\\\\\fnMicrosoftfnMicrosoft\\\\\\\\\fn {2}}	1	− − 13{textstyle -{frac {1}{3}}	− − 13{textstyle -{frac {1}{3}}
Combustible de miel cúbica		JUEGO	JUEGO	JUEGO	6	12	3	4	Bipyramid cuadrado		1{textstyle 1}	0.866	− − 12{textstyle -{frac {1}{2}}}	0{textstyle 0}
Rectificado 600 celdas		720	120	600	12	6	3	3	Bipirámide pentagonal		5+355{fnMicroc {5+3{sqrt {}} {5}}} {}}} {}}}} {}}}}} {}}}} {}}} {}}}} {}}}} {}}}}} {}}}} {}}}}} {}}}}}} {}}}}}}}} {}}}} {}}}}}}}}} {}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}} {}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}	1.447	− − 11+4541{textstyle -{frac {11+4{sqrt {}} {41}}} {}}} {}}}} {}}}}} {}}} {}}} {}}} {}}}} {}}}}} {}}}}} {}}}} {}}}}} {}}}}} {}}}}}} {}}}}}} {}}}}}}} {}}}}}}} {}}}}}}} {}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}} {}}}}} {}}}}}}} {}}}}}}}} {}}}}}}}}}}}}}} {} {}}}} {}}}}}}} {}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}	− − 11+4541{textstyle -{frac {11+4{sqrt {}} {41}}} {}}} {}}}} {}}}}} {}}} {}}} {}}} {}}}} {}}}}} {}}}}} {}}}} {}}}}} {}}}}} {}}}}}} {}}}}}} {}}}}}}} {}}}}}}} {}}}}}}} {}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}} {}}}}} {}}}}}}} {}}}}}}}} {}}}}}}}}}}}}}} {} {}}}} {}}}}}}} {}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}

* Las 16 celdas rectificadas son las 24 celdas regulares y los vértices son equivalentes: la octahedra son bipirámides regulares.

# Dado numéricamente debido a una forma más compleja.

Otras dimensiones

En general, una bipirámide puede verse como un politopo n construido con un politopo (n − 1) en un hiperplano con dos puntos en direcciones opuestas e iguales distancias perpendiculares al hiperplano. Si el politopo (n − 1) es un politopo regular, tendrá facetas piramidales idénticas.

Una pirámide bidimensional (y #34;regular ") simétrica recta (diagonal) se forma al unir dos triángulos isósceles congruentes de base a base; su contorno es un rombo, {}+{}.

Bipirámides poliédricas

Una bipirámide poliédrica es un politopo de 4 con una base de poliedro y un punto de vértice.

Un ejemplo es el de 16 celdas, que es una bipirámide octaédrica, {}+{3,4}, y más generalmente un ortoplex n es un (n − 1)-bipirámide orthoplex, {}+{3^n-2,4}.

Otras bipirámides incluyen la bipirámide tetraédrica, {}+{3,3}, la bipirámide icosaédrica, {}+{3,5}, y la bipirámide dodecaédrica, {}+{5,3}, siendo las dos primeras todas regulares células, también son politopos ciegos.