Bioestadística
Bioestadística (también conocida como biometría) es el desarrollo y la aplicación de métodos estadísticos a una amplia gama de temas en biología. Abarca el diseño de experimentos biológicos, la recopilación y el análisis de datos de esos experimentos y la interpretación de los resultados.
Historia
Bioestadística y genética
El modelado bioestadístico forma una parte importante de numerosas teorías biológicas modernas. Los estudios de genética, desde sus inicios, utilizaron conceptos estadísticos para comprender los resultados experimentales observados. Algunos científicos genéticos incluso contribuyeron con avances estadísticos con el desarrollo de métodos y herramientas. Gregor Mendel inició los estudios genéticos investigando los patrones de segregación genética en familias de guisantes y usó estadísticas para explicar los datos recopilados. A principios del siglo XX, después del redescubrimiento del trabajo de herencia mendeliana de Mendel, hubo lagunas en la comprensión entre la genética y el darwinismo evolutivo. Francis Galton intentó expandir los descubrimientos de Mendel con datos humanos y propuso un modelo diferente con fracciones de la herencia provenientes de cada ancestral componiendo una serie infinita. Llamó a esto la teoría de la 'Ley de Herencia Ancestral'. Sus ideas fueron fuertemente discrepadas por William Bateson, quien siguió las conclusiones de Mendel, que la herencia genética era exclusivamente de los padres, la mitad de cada uno de ellos. Esto condujo a un vigoroso debate entre los biometristas, que apoyaban las ideas de Galton, como Raphael Weldon, Arthur Dukinfield Darbishire y Karl Pearson, y los mendelianos, que apoyaban las ideas de Bateson (y Mendel), como Charles Davenport y Wilhelm Johannsen. Más tarde, los biometristas no pudieron reproducir las conclusiones de Galton en diferentes experimentos, y prevalecieron las ideas de Mendel. En la década de 1930, los modelos basados en el razonamiento estadístico habían ayudado a resolver estas diferencias y a producir la síntesis evolutiva moderna neodarwinista.
Resolver estas diferencias también permitió definir el concepto de genética de poblaciones y unió genética y evolución. Las tres figuras principales en el establecimiento de la genética de poblaciones y esta síntesis se basaron en estadísticas y desarrollaron su uso en biología.
- Ronald Fisher colaboró junto con la estadística Betty Allan desarrollando varios métodos estadísticos básicos en apoyo de su trabajo estudiando los experimentos de cultivos en Rothamsted Research, publicados en los libros de Fisher Métodos estadísticos para los trabajadores de investigación (1925) y The Genetical Theory of Natural Selection (1930), así como los documentos científicos de Allan. Fisher siguió dando muchas contribuciones a la genética y las estadísticas. Algunos de ellos incluyen los conceptos ANOVA, p-valor, la prueba exacta de Fisher y la ecuación de Fisher para la dinámica demográfica. Se le acredita por la frase "La selección natural es un mecanismo para generar un alto grado de improbabilidad".
- Sewall G. Wright desarrolló F-estadísticas y métodos de computación y definió coeficiente de endogamiento.
- El libro de J. B. S. Haldane, Las causas de la evolución, restableció la selección natural como el principal mecanismo de evolución explicándola en términos de las consecuencias matemáticas de la genética mendeliana. También desarrolló la teoría de la sopa primordial.
Estos y otros bioestadísticos, biólogos matemáticos y genetistas inclinados a la estadística ayudaron a unir la biología evolutiva y la genética en un todo consistente y coherente que podría comenzar a modelarse cuantitativamente.
Paralelamente a este desarrollo general, el trabajo pionero de D'Arcy Thompson en Sobre el crecimiento y la forma también ayudó a agregar disciplina cuantitativa al estudio biológico.
A pesar de la importancia fundamental y la necesidad frecuente del razonamiento estadístico, puede haber una tendencia entre los biólogos a desconfiar o menospreciar los resultados que no son cualitativamente aparentes. Una anécdota describe a Thomas Hunt Morgan prohibiendo la calculadora Friden de su departamento en Caltech, diciendo: "Bueno, soy como un tipo que busca oro a lo largo de las orillas del río Sacramento en 1849. Con un poco de inteligencia, puedo agacharse y recoger grandes pepitas de oro. Y mientras pueda hacer eso, no permitiré que ninguna persona de mi departamento desperdicie recursos escasos en la extracción de placeres."
Planificación de la investigación
Cualquier investigación en ciencias de la vida se propone para responder a una pregunta científica que podamos tener. Para responder a esta pregunta con un alto grado de certeza, necesitamos resultados precisos. La definición correcta de la hipótesis principal y el plan de investigación reducirá los errores al tomar una decisión en la comprensión de un fenómeno. El plan de investigación puede incluir la pregunta de investigación, la hipótesis a probar, el diseño experimental, los métodos de recopilación de datos, las perspectivas de análisis de datos y los costos involucrados. Es fundamental llevar a cabo el estudio con base en los tres principios básicos de la estadística experimental: aleatorización, replicación y control local.
Pregunta de investigación
La pregunta de investigación definirá el objetivo de un estudio. La investigación estará encabezada por la pregunta, por lo que debe ser concisa, al mismo tiempo que se centre en temas interesantes y novedosos que puedan mejorar la ciencia y el conocimiento en ese campo. Para definir la forma de formular la pregunta científica, puede ser necesaria una revisión exhaustiva de la literatura. Por lo que la investigación puede ser útil para agregar valor a la comunidad científica.
Definición de hipótesis
Una vez definido el objetivo del estudio, se pueden proponer las posibles respuestas a la pregunta de investigación, transformando esta pregunta en una hipótesis. La principal propuesta se denomina hipótesis nula (H0) y suele basarse en un conocimiento permanente sobre el tema o en una ocurrencia evidente de los fenómenos, sustentada en una revisión profunda de la literatura. Podemos decir que es la respuesta esperada estándar para los datos bajo la situación en prueba. En general, HO no asume ninguna asociación entre tratamientos. Por otro lado, la hipótesis alternativa es la negación de HO. Supone cierto grado de asociación entre el tratamiento y el resultado. Si bien, la hipótesis se sustenta en la investigación de preguntas y sus respuestas esperadas e inesperadas.
Como ejemplo, considere grupos de animales similares (ratones, por ejemplo) bajo dos sistemas de dieta diferentes. La pregunta de investigación sería: ¿cuál es la mejor dieta? En este caso, H0 sería que no hay diferencia entre las dos dietas en el metabolismo de los ratones (H0: μ1 = μ2) y la hipótesis alternativa sería que las dietas tienen efectos diferentes sobre el metabolismo de los animales (H1: μ1 ≠ μ2).
La hipótesis es definida por el investigador, de acuerdo a sus intereses en responder la pregunta principal. Además de eso, la hipótesis alternativa puede ser más de una hipótesis. Puede suponer no solo diferencias entre los parámetros observados, sino también su grado de diferencias (es decir, mayor o menor).
Muestreo
Por lo general, un estudio tiene como objetivo comprender el efecto de un fenómeno sobre una población. En biología, una población se define como todos los individuos de una especie dada, en un área específica en un momento dado. En bioestadística, este concepto se extiende a una variedad de colecciones posibles de estudio. Aunque, en bioestadística, una población no son solo los individuos, sino el total de un componente específico de sus organismos, como el genoma completo, o todos los espermatozoides, para los animales, o el área foliar total, para una planta, por ejemplo.
No es posible tomar las medidas de todos los elementos de una población. Por eso, el proceso de muestreo es muy importante para la inferencia estadística. El muestreo se define como obtener aleatoriamente una parte representativa de toda la población, para hacer inferencias posteriores sobre la población. Por lo tanto, la muestra podría captar la mayor variabilidad en una población. El tamaño de la muestra está determinado por varias cosas, desde el alcance de la investigación hasta los recursos disponibles. En la investigación clínica, el tipo de ensayo, como inferioridad, equivalencia y superioridad es clave para determinar el tamaño de la muestra.
Diseño experimental
Los diseños experimentales sostienen esos principios básicos de las estadísticas experimentales. Hay tres diseños experimentales básicos para asignar aleatoriamente los tratamientos en todas las parcelas del experimento. Son el diseño completamente al azar, el diseño de bloques al azar y el diseño factorial. Los tratamientos se pueden organizar de muchas maneras dentro del experimento. En agricultura, el diseño experimental correcto es la raíz de un buen estudio y la disposición de los tratamientos dentro del estudio es fundamental porque el ambiente afecta en gran medida a las parcelas (plantas, ganado, microorganismos). Estos arreglos principales se pueden encontrar en la literatura bajo los nombres de "lattices", "bloques incompletos", "parcela dividida", "bloques aumentados";, y muchos otros. Todos los diseños pueden incluir gráficos de control, determinados por el investigador, para proporcionar una estimación del error durante la inferencia.
En los estudios clínicos, las muestras suelen ser más pequeñas que en otros estudios biológicos y, en la mayoría de los casos, el efecto ambiental se puede controlar o medir. Es común el uso de ensayos clínicos controlados aleatorizados, donde los resultados se suelen comparar con diseños de estudios observacionales como el de casos y controles o el de cohortes.
Recopilación de datos
Los métodos de recopilación de datos deben tenerse en cuenta en la planificación de la investigación, ya que influye mucho en el tamaño de la muestra y el diseño experimental.
La recopilación de datos varía según el tipo de datos. Para datos cualitativos, la recolección se puede hacer con cuestionarios estructurados o por observación, considerando la presencia o intensidad de la enfermedad, utilizando el criterio de puntuación para categorizar los niveles de ocurrencia. Para datos cuantitativos, la recopilación se realiza midiendo información numérica utilizando instrumentos.
En los estudios de agricultura y biología, los datos de rendimiento y sus componentes se pueden obtener mediante medidas métricas. Sin embargo, las lesiones por plagas y enfermedades en las parcelas se obtienen por observación, considerando escalas de puntuación para los niveles de daño. Especialmente, en estudios genéticos, se deben considerar métodos modernos para la recopilación de datos en campo y laboratorio, como plataformas de alto rendimiento para el fenotipado y el genotipado. Estas herramientas permiten experimentos más grandes, al mismo tiempo que permiten evaluar muchas parcelas en menos tiempo que un método solo basado en humanos para la recopilación de datos. Finalmente, todos los datos recopilados de interés deben almacenarse en un marco de datos organizado para su posterior análisis.
Análisis e interpretación de datos
Herramientas descriptivas
Los datos se pueden representar a través de tablas o representaciones gráficas, como gráficos de líneas, gráficos de barras, histogramas, diagramas de dispersión. Además, las medidas de tendencia central y variabilidad pueden ser muy útiles para describir una visión general de los datos. Sigue algunos ejemplos:
Tablas de frecuencia
Un tipo de tablas son las tablas de frecuencia, que consisten en datos organizados en filas y columnas, donde la frecuencia es el número de ocurrencias o repeticiones de datos. La frecuencia puede ser:
Absoluto: representa el número de veces que aparece un determinado valor;
Relativo: obtenido por la división de la frecuencia absoluta por el número total;
En el siguiente ejemplo, tenemos el número de genes en diez operones del mismo organismo.
- Genes = {2,3,3,4,5,3,3,3,3,3,4}
| Número de genes | Frecuencia absoluta | Frecuencia relativa |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 1 | 0.1 |
| 3 | 6 | 0.6 |
| 4 | 2 | 0.2 |
| 5 | 1 | 0.1 |
Gráfico de líneas

Los gráficos de líneas representan la variación de un valor sobre otra métrica, como el tiempo. En general, los valores se representan en el eje vertical, mientras que la variación temporal se representa en el eje horizontal.
Gráfico de barras
Un gráfico de barras es un gráfico que muestra datos categóricos como barras que presentan alturas (barra vertical) o anchos (barra horizontal) proporcionales para representar valores. Los gráficos de barras proporcionan una imagen que también podría representarse en un formato tabular.
En el ejemplo del gráfico de barras, tenemos la tasa de natalidad en Brasil para los meses de diciembre de 2010 a 2016. La fuerte caída en diciembre de 2016 refleja el brote del virus Zika en la tasa de natalidad en Brasil.
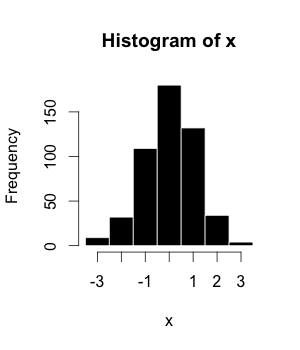
Histogramas
El histograma (o distribución de frecuencia) es una representación gráfica de un conjunto de datos tabulado y dividido en clases uniformes o no uniformes. Fue introducido por primera vez por Karl Pearson.
Gráfico de dispersión
Un gráfico de dispersión es un diagrama matemático que utiliza coordenadas cartesianas para mostrar los valores de un conjunto de datos. Un gráfico de dispersión muestra los datos como un conjunto de puntos, cada uno de los cuales presenta el valor de una variable que determina la posición en el eje horizontal y otra variable en el eje vertical. También se denominan gráfico de dispersión, gráfico de dispersión, diagrama de dispersión o diagrama de dispersión.
Media
La media aritmética es la suma de una colección de valores (x1+x2+x3+⋯ ⋯ +xn{displaystyle {x_{1}+x_{2}+x_{3}+cdots #) dividido por el número de elementos de esta colección (n{displaystyle {n}).
- x̄ ̄ =1n().. i=1nxi)=x1+x2+⋯ ⋯ +xnn{displaystyle {bar {x}={frac {1}{n}left(sum)} ¿Por qué? {x_{1}+x_{2}+cdots - Sí.
Mediana
La mediana es el valor en el medio de un conjunto de datos.
Modo
La moda es el valor de un conjunto de datos que aparece con mayor frecuencia.
| Tipo | Ejemplo | Resultado |
|---|---|---|
| Significa | (2 + 3 + 3 + 3 + 3 + 3 + 4 + 4 + 11) / 9 | 4 |
| Mediano | 2, 3, 3, 3, 3, 3, 4, 4, 11 | 3 |
| Modo | 2, 3, 3, 3, 3, 3, 4, 4, 11 | 3 |
Diagrama de caja
El diagrama de caja es un método para representar gráficamente grupos de datos numéricos. Los valores máximo y mínimo están representados por las líneas, y el rango intercuartil (IQR) representa el 25-75% de los datos. Los valores atípicos se pueden trazar como círculos.
Coeficientes de correlación
Aunque las correlaciones entre dos tipos diferentes de datos pueden inferirse mediante gráficos, como un diagrama de dispersión, es necesario validar esto a través de información numérica. Por esta razón, se requieren coeficientes de correlación. Proporcionan un valor numérico que refleja la fuerza de una asociación.
Coeficiente de correlación de Pearson
El coeficiente de correlación de Pearson es una medida de asociación entre dos variables, X e Y. Este coeficiente, generalmente representado por ρ (rho) para la población y r para la muestra, asume valores entre −1 y 1, donde ρ = 1 representa una correlación positiva perfecta, ρ = −1 representa una correlación negativa perfecta y ρ = 0 no hay correlación lineal.
Estadísticas inferenciales
Se utiliza para hacer inferencias sobre una población desconocida, por estimación y/o prueba de hipótesis. En otras palabras, es deseable obtener parámetros para describir la población de interés, pero dado que los datos son limitados, es necesario hacer uso de una muestra representativa para poder estimarlos. Con eso, es posible probar hipótesis previamente definidas y aplicar las conclusiones a toda la población. El error estándar de la media es una medida de variabilidad que es crucial para hacer inferencias.
- Pruebas de hipotesis
La prueba de hipótesis es esencial para hacer inferencias sobre poblaciones con el objetivo de responder preguntas de investigación, como se establece en "Planificación de la investigación" sección. Los autores definieron cuatro pasos a establecer:
- La hipótesis a ser probada: como se indicó anteriormente, tenemos que trabajar con la definición de una hipótesis nula (H)0), que va a ser probado, y una hipótesis alternativa. Pero deben definirse antes de la implementación del experimento.
- Nivel de significación y regla de decisión: Una regla de decisión depende del nivel de significado, o en otras palabras, de la tasa de error aceptable (α). Es más fácil pensar que definimos un valor crítico que determina el significado estadístico cuando se compara una estadística de prueba con ella. Así, α también tiene que ser predefinido antes del experimento.
- Análisis experimental y estadístico: Esto es cuando el experimento se implementa realmente después del diseño experimental apropiado, se recopilan datos y se evalúan las pruebas estadísticas más adecuadas.
- Inferencias: Se hace cuando la hipótesis nula es rechazada o no rechazada, basándose en la evidencia de que la comparación de p-valores y α trae. Se señala que el fracaso de rechazar H0 sólo significa que no hay suficiente evidencia para apoyar su rechazo, pero no que esta hipótesis sea verdadera.
- Intervalos de confianza
Un intervalo de confianza es un rango de valores que puede contener el verdadero valor real del parámetro dado un cierto nivel de confianza. El primer paso es estimar la mejor estimación imparcial del parámetro de la población. El valor superior del intervalo se obtiene por la suma de esta estimación con la multiplicación entre el error estándar de la media y el nivel de confianza. El cálculo del valor inferior es similar, pero en lugar de una suma, se debe aplicar una resta.
Consideraciones estadísticas
Potencia y error estadístico
Al probar una hipótesis, hay dos tipos de errores estadísticos posibles: error de tipo I y error de tipo II. El error tipo I o falso positivo es el rechazo incorrecto de una hipótesis nula verdadera y el error tipo II o falso negativo es el fracaso en rechazar una hipótesis nula falsa. El nivel de significación denotado por α es la tasa de error tipo I y debe elegirse antes de realizar la prueba. La tasa de error tipo II se denota por β y el poder estadístico de la prueba es 1 − β.
Valor P
El valor p es la probabilidad de obtener resultados tan extremos o más extremos que los observados, asumiendo que la hipótesis nula (H0) es verdadera. También se le llama probabilidad calculada. Es común confundir el valor p con el nivel de significación (α), pero el α es un umbral predefinido para llamar resultados significativos. Si p es menor que α, se rechaza la hipótesis nula (H0).
Múltiples pruebas
En múltiples pruebas de la misma hipótesis, la probabilidad de ocurrencia de falsos positivos (tasa de error familiar) aumenta y se utiliza alguna estrategia para controlar esta ocurrencia. Esto se logra comúnmente mediante el uso de un umbral más estricto para rechazar hipótesis nulas. La corrección de Bonferroni define un nivel de significación global aceptable, denotado por α* y cada prueba se compara individualmente con un valor de α = α*/m. Esto asegura que la tasa de error familiar en todas las m pruebas sea menor o igual a α*. Cuando m es grande, la corrección de Bonferroni puede ser demasiado conservadora. Una alternativa a la corrección de Bonferroni es controlar la tasa de descubrimiento falso (FDR). El FDR controla la proporción esperada de hipótesis nulas rechazadas (los llamados descubrimientos) que son falsas (rechazos incorrectos). Este procedimiento asegura que, para pruebas independientes, la tasa de descubrimiento falso sea como máximo q*. Así, la FDR es menos conservadora que la corrección de Bonferroni y tiene más potencia, a costa de más falsos positivos.
Comprobaciones de robustez y especificación incorrecta
La hipótesis principal que se prueba (p. ej., la ausencia de asociación entre los tratamientos y los resultados) suele ir acompañada de otras suposiciones técnicas (p. ej., sobre la forma de la distribución de probabilidad de los resultados) que también forman parte de la hipótesis nula. Cuando los supuestos técnicos se violan en la práctica, la hipótesis nula puede rechazarse con frecuencia incluso si la hipótesis principal es verdadera. Se dice que tales rechazos se deben a una especificación incorrecta del modelo. Verificar si el resultado de una prueba estadística no cambia cuando los supuestos técnicos se modifican ligeramente (los llamados controles de robustez) es la principal forma de combatir la especificación errónea.
Criterios de selección del modelo
La selección de criterios de modelo seleccionará o modelará ese modelo verdadero más aproximado. El criterio de información de Akaike (AIC) y el criterio de información bayesiano (BIC) son ejemplos de criterios asintóticamente eficientes.
Desarrollos y big data
Los desarrollos recientes han tenido un gran impacto en la bioestadística. Dos cambios importantes han sido la capacidad de recopilar datos en una escala de alto rendimiento y la capacidad de realizar análisis mucho más complejos utilizando técnicas computacionales. Esto proviene del desarrollo en áreas como tecnologías de secuenciación, Bioinformática y Machine learning (Machine learning en bioinformática).
Uso en datos de alto rendimiento
Las nuevas tecnologías biomédicas, como los microarrays, los secuenciadores de próxima generación (para genómica) y la espectrometría de masas (para proteómica), generan enormes cantidades de datos, lo que permite realizar muchas pruebas simultáneamente. Se requiere un análisis cuidadoso con métodos bioestadísticos para separar la señal del ruido. Por ejemplo, una micromatriz podría usarse para medir muchos miles de genes simultáneamente, determinando cuáles de ellos tienen una expresión diferente en las células enfermas en comparación con las células normales. Sin embargo, solo una fracción de genes se expresará diferencialmente.
La multicolinealidad suele ocurrir en entornos bioestadísticos de alto rendimiento. Debido a la alta intercorrelación entre los predictores (como los niveles de expresión génica), la información de un predictor puede estar contenida en otro. Podría ser que sólo el 5% de los predictores sean responsables del 90% de la variabilidad de la respuesta. En tal caso, se podría aplicar la técnica bioestadística de reducción de dimensiones (por ejemplo, a través del análisis de componentes principales). Las técnicas estadísticas clásicas como la regresión lineal o logística y el análisis discriminante lineal no funcionan bien para datos de gran dimensión (es decir, cuando el número de observaciones n es menor que el número de características o predictores p: n < p). De hecho, se pueden obtener valores R2 bastante altos a pesar del poder predictivo muy bajo del modelo estadístico. Estas técnicas estadísticas clásicas (especialmente la regresión lineal de mínimos cuadrados) se desarrollaron para datos de baja dimensión (es decir, donde el número de observaciones n es mucho mayor que el número de predictores p: n >> p). En casos de alta dimensionalidad, siempre se debe considerar un conjunto de prueba de validación independiente y la correspondiente suma residual de cuadrados (RSS) y R2 del conjunto de prueba de validación, no los del conjunto de entrenamiento.
A menudo, es útil agrupar información de varios predictores. Por ejemplo, el análisis de enriquecimiento de conjuntos de genes (GSEA) considera la perturbación de conjuntos de genes completos (funcionalmente relacionados) en lugar de genes individuales. Estos conjuntos de genes pueden ser rutas bioquímicas conocidas o genes funcionalmente relacionados de otro modo. La ventaja de este enfoque es que es más robusto: es más probable que se encuentre que un solo gen está falsamente perturbado que que toda una vía está falsamente perturbada. Además, uno puede integrar el conocimiento acumulado sobre las vías bioquímicas (como la vía de señalización JAK-STAT) utilizando este enfoque.
Avances bioinformáticos en bases de datos, minería de datos e interpretación biológica
El desarrollo de bases de datos biológicas permite el almacenamiento y la gestión de datos biológicos con la posibilidad de garantizar el acceso a usuarios de todo el mundo. Son útiles para los investigadores que depositan datos, recuperan información y archivos (en bruto o procesados) originados a partir de otros experimentos o indexan artículos científicos, como PubMed. Otra posibilidad es buscar el término deseado (un gen, una proteína, una enfermedad, un organismo, etc.) y consultar todos los resultados relacionados con esta búsqueda. Existen bases de datos dedicadas a los SNP (dbSNP), el conocimiento sobre la caracterización de genes y sus vías (KEGG) y la descripción de la función de los genes clasificándolos por componente celular, función molecular y proceso biológico (Gene Ontology). Además de las bases de datos que contienen información molecular específica, existen otras que son amplias en el sentido de que almacenan información sobre un organismo o grupo de organismos. Como ejemplo de una base de datos dirigida a un solo organismo, pero que contiene muchos datos sobre él, es la base de datos genética y molecular de Arabidopsis thaliana - TAIR. Phytozome, a su vez, almacena los ensamblajes y archivos de anotaciones de docenas de genomas de plantas, y también contiene herramientas de visualización y análisis. Además, existe una interconexión entre algunas bases de datos en el intercambio/intercambio de información y una iniciativa importante fue la Colaboración internacional de bases de datos de secuencias de nucleótidos (INSDC), que relaciona datos de DDBJ, EMBL-EBI y NCBI.
Hoy en día, el aumento en el tamaño y la complejidad de los conjuntos de datos moleculares conduce al uso de poderosos métodos estadísticos proporcionados por algoritmos informáticos desarrollados por el área de aprendizaje automático. Por lo tanto, la minería de datos y el aprendizaje automático permiten detectar patrones en datos con una estructura compleja, como los biológicos, mediante el uso de métodos de aprendizaje supervisado y no supervisado, regresión, detección de clústeres y minería de reglas de asociación, entre otros. Para indicar algunos de ellos, los mapas autoorganizados y k-means son ejemplos de algoritmos de conglomerados; La implementación de redes neuronales y los modelos de máquinas de vectores de soporte son ejemplos de algoritmos de aprendizaje automático comunes.
El trabajo colaborativo entre biólogos moleculares, bioinformáticos, estadísticos e informáticos es importante para realizar correctamente un experimento, desde la planificación, pasando por la generación y análisis de datos, hasta la interpretación biológica de los resultados.
Uso de métodos computacionalmente intensivos
Por otro lado, el advenimiento de la tecnología informática moderna y los recursos informáticos relativamente baratos han permitido métodos bioestadísticos intensivos en computación, como los métodos de arranque y remuestreo.
En los últimos tiempos, los bosques aleatorios han ganado popularidad como método para realizar la clasificación estadística. Las técnicas de bosque aleatorio generan un panel de árboles de decisión. Los árboles de decisión tienen la ventaja de que puede dibujarlos e interpretarlos (incluso con conocimientos básicos de matemáticas y estadística). Los bosques aleatorios se han utilizado por lo tanto para los sistemas de apoyo a la toma de decisiones clínicas.
Aplicaciones
Salud pública
Salud pública, incluida la epidemiología, la investigación de los servicios de salud, la nutrición, la salud ambiental y la política de atención de la salud & administración. En estos contenidos de medicamentos es importante considerar el diseño y análisis de los ensayos clínicos. Como un ejemplo, está la evaluación del estado de gravedad de un paciente con un pronóstico del resultado de una enfermedad.
Con las nuevas tecnologías y el conocimiento de la genética, la bioestadística ahora también se utiliza para la medicina de Sistemas, que consiste en una medicina más personalizada. Para ello, se realiza una integración de datos de diferentes fuentes, incluyendo datos de pacientes convencionales, parámetros clínico-patológicos, datos moleculares y genéticos así como datos generados por tecnologías adicionales de nueva ómica.
Genética cuantitativa
El estudio de la genética de poblaciones y la genética estadística para relacionar la variación del genotipo con la variación del fenotipo. En otras palabras, es deseable descubrir la base genética de un rasgo medible, un rasgo cuantitativo, que está bajo control poligénico. Una región del genoma que es responsable de un rasgo continuo se denomina locus de rasgos cuantitativos (QTL). El estudio de los QTL se vuelve factible mediante el uso de marcadores moleculares y la medición de rasgos en las poblaciones, pero su mapeo necesita la obtención de una población a partir de un cruce experimental, como un F2 o cepas/líneas endogámicas recombinantes (RIL). Para buscar regiones de QTL en un genoma, se debe construir un mapa de genes basado en el enlace. Algunos de los algoritmos de mapeo de QTL más conocidos son el mapeo de intervalos, el mapeo de intervalos compuestos y el mapeo de intervalos múltiples.
Sin embargo, la resolución del mapeo de QTL se ve afectada por la cantidad de recombinación analizada, un problema para las especies en las que es difícil obtener descendencia grande. Además, la diversidad de alelos está restringida a individuos originados de padres contrastantes, lo que limita los estudios de diversidad de alelos cuando tenemos un panel de individuos que representan una población natural. Por esta razón, se propuso el estudio de asociación Genome-wide para identificar QTL basados en el desequilibrio de ligamiento, es decir, la asociación no aleatoria entre rasgos y marcadores moleculares. Fue aprovechado por el desarrollo de genotipado SNP de alto rendimiento.
En fitomejoramiento animal y vegetal, el uso de marcadores en la selección con fines de mejoramiento, principalmente los moleculares, colaboró al desarrollo de la selección asistida por marcadores. Si bien el mapeo de QTL tiene una resolución limitada, GWAS no tiene suficiente poder cuando las variantes raras de pequeño efecto también están influenciadas por el entorno. Surge entonces el concepto de Selección Genómica (GS) con el fin de utilizar todos los marcadores moleculares en la selección y permitir la predicción del desempeño de los candidatos en esta selección. La propuesta es genotipar y fenotipar una población de entrenamiento, desarrollar un modelo que pueda obtener los valores reproductivos estimados genómicos (GEBVs) de individuos pertenecientes a una población genotípica pero no fenotípica, denominada población de prueba. Este tipo de estudio también podría incluir una población de validación, pensando en el concepto de validación cruzada, en el que los resultados fenotípicos reales medidos en esta población se comparan con los resultados fenotípicos basados en la predicción, lo que se utiliza para comprobar la precisión del modelo..
A modo de resumen, algunos puntos sobre la aplicación de la genética cuantitativa son:
- Esto se ha utilizado en la agricultura para mejorar los cultivos (creación de plantas) y el ganado (creación animal).
- En la investigación biomédica, este trabajo puede ayudar a encontrar candidatos alelos gen que pueden causar o influir la predisposición a enfermedades en la genética humana
Datos de expresión
Los estudios para la expresión diferencial de genes a partir de datos de RNA-Seq, como para RT-qPCR y microarrays, exigen la comparación de condiciones. El objetivo es identificar genes que tengan un cambio significativo en la abundancia entre diferentes condiciones. Luego, los experimentos se diseñan adecuadamente, con réplicas para cada condición/tratamiento, aleatorización y bloqueo, cuando sea necesario. En RNA-Seq, la cuantificación de la expresión utiliza la información de lecturas mapeadas que se resumen en alguna unidad genética, como exones que forman parte de una secuencia de genes. Dado que los resultados de los microarrays se pueden aproximar mediante una distribución normal, los datos de recuentos de RNA-Seq se explican mejor mediante otras distribuciones. La primera distribución utilizada fue la de Poisson, pero subestima el error muestral, dando lugar a falsos positivos. Actualmente, la variación biológica es considerada por métodos que estiman un parámetro de dispersión de una distribución binomial negativa. Se utilizan modelos lineales generalizados para realizar las pruebas de significación estadística y, dado que el número de genes es alto, se debe considerar la corrección de múltiples pruebas. Algunos ejemplos de otros análisis de datos genómicos provienen de experimentos de microarrays o proteómica. A menudo en relación con las enfermedades o etapas de la enfermedad.
Otros estudios
- Ecología, pronóstico ecológico
- Análisis de secuencias biológicas
- Biología de sistemas para análisis de inferencias o vías de red genéticas.
- Investigación clínica y desarrollo farmacéutico
- Dinámica de la población, especialmente en lo que respecta a la ciencia pesquera.
- Filogenética y evolución
- Farmacodynamics
- Farmacocinética
- Neuroimagen
Herramientas
Existen muchas herramientas que se pueden utilizar para realizar análisis estadísticos en datos biológicos. La mayoría de ellos son de utilidad en otras áreas del conocimiento, abarcando un gran número de aplicaciones (por orden alfabético). Aquí hay una breve descripción de algunos de ellos:
- ASReml: Otro software desarrollado por VSNi que puede ser utilizado también en el entorno R como un paquete. Está diseñado para estimar componentes de varianza bajo un modelo mixto lineal general utilizando la probabilidad máxima restringida (REML). Se permiten modelos con efectos fijos y efectos aleatorios y anidados o cruzados. Da la posibilidad de investigar diferentes estructuras de matriz de varianza-covariancia.
- CycDesigN: Un paquete informático desarrollado por VSNi que ayuda a los investigadores a crear diseños experimentales y analizar datos procedentes de un diseño presente en una de las tres clases manejadas por CycDesigN. Estas clases son diseños resolvables, no resolvables, parcialmente replicados y cruzados. Incluye diseños menos usados los latinos, como diseño t latinizado.
- Orange: Una interfaz de programación para el procesamiento de datos de alto nivel, la extracción de datos y la visualización de datos. Incluye herramientas para la expresión de genes y la genómica.
- R: Un ambiente de código abierto y lenguaje de programación dedicado a la informática y los gráficos estadísticos. Es una implementación del lenguaje S mantenido por CRAN. Además de sus funciones de leer tablas de datos, tomar estadísticas descriptivas, desarrollar y evaluar modelos, su repositorio contiene paquetes desarrollados por investigadores de todo el mundo. Esto permite el desarrollo de funciones escritas para tratar el análisis estadístico de datos que proviene de aplicaciones específicas. En el caso de Bioinformática, por ejemplo, hay paquetes ubicados en el repositorio principal (CRAN) y en otros, como Bioconductor. También es posible utilizar paquetes en desarrollo que se comparten en los servicios de alojamiento como GitHub.
- SAS: Un software de análisis de datos ampliamente utilizado, pasando por universidades, servicios e industria. Desarrollado por una empresa con el mismo nombre (SAS Institute), utiliza lenguaje SAS para la programación.
- PLA 3.0: Es un software de análisis bioestadístico para entornos regulados (por ejemplo, pruebas de drogas) que admite ensayos cuantitativos de respuesta (Parallel-Line, Parallel-Logistics, Slope-Ratio) y Ensayos Dichotomosos (Respuesta Cuantal, Ensayos binarios). También soporta métodos de ponderación para cálculos combinados y la agregación automática de datos de ensayos independientes.
- Weka: Un software Java para el aprendizaje automático y la minería de datos, incluyendo herramientas y métodos para la visualización, agrupación, regresión, regla de asociación y clasificación. Hay herramientas para la validación cruzada, arranque y un módulo de comparación de algoritmos. Weka también se puede ejecutar en otros idiomas de programación como Perl o R.
- Python (lengua de programación) análisis de imágenes, aprendizaje profundo, aprendizaje automático
- Bases de datos SQL
- NoSQL
- NumPy pitón numérico
- SciPy
- SageMath
- Álgebra lineal LAPACK
- MATLAB
- Apache Hadoop
- Apache Spark
- Amazon Web Services
Alcance y programas de formación
Casi todos los programas educativos en bioestadística son a nivel de posgrado. Se encuentran con mayor frecuencia en escuelas de salud pública, afiliadas a escuelas de medicina, silvicultura o agricultura, o como foco de aplicación en departamentos de estadística.
En los Estados Unidos, donde varias universidades tienen departamentos de bioestadística dedicados, muchas otras universidades de primer nivel integran facultades de bioestadística en estadísticas u otros departamentos, como epidemiología. Por lo tanto, los departamentos que llevan el nombre de "bioestadística" pueden existir bajo estructuras muy diferentes. Por ejemplo, se han fundado departamentos de bioestadística relativamente nuevos con un enfoque en bioinformática y biología computacional, mientras que los departamentos más antiguos, generalmente afiliados a escuelas de salud pública, tendrán líneas de investigación más tradicionales que involucran estudios epidemiológicos y ensayos clínicos, así como bioinformática. En las universidades más grandes de todo el mundo, donde existen departamentos de estadística y bioestadística, el grado de integración entre los dos departamentos puede variar desde el mínimo indispensable hasta una colaboración muy estrecha. En general, la diferencia entre un programa de estadística y un programa de bioestadística es doble: (i) los departamentos de estadística suelen albergar investigaciones teóricas/metodológicas que son menos comunes en los programas de bioestadística y (ii) los departamentos de estadística tienen líneas de investigación que pueden incluir aplicaciones biomédicas. pero también otras áreas como la industria (control de calidad), negocios y economía y áreas biológicas distintas a la medicina.
Revistas especializadas
- Bioestadística
- International Journal of Biostatistics
- Journal of Epidemiology and Biostatistics
- Bioestadística y Salud Pública
- Biometrics
- Biometrika
- Biometrical Journal
- Comunicaciones en Biometría y Ciencia de Cultivos
- Aplicaciones Estadística en Genética y Biología Molecular
- Métodos estadísticos en investigación médica
- Estadísticas farmacéuticas
- Estadísticas en Medicina
Contenido relacionado
Trofim Lisenko
Pedro scott
ARN