Beta termodinámica

En la termodinámica estadística, termodinámica beta, también conocido como frío, es la reciproca de la temperatura termodinámica de un sistema:

β β =1kBT{displaystyle beta ={frac {1}{k_{rm {B}T}}

Fue introducida originalmente en 1971 (como Kältefunktion "función de frialdad") por Ingo Müller [de], uno de los defensores de la escuela de pensamiento de la termodinámica racional, basada en anteriores propuestas para una "temperatura recíproca" función.

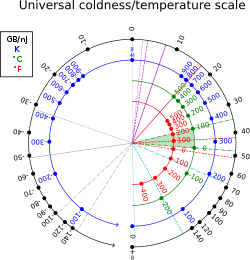
La beta termodinámica tiene unidades recíprocas a la de la energía (en unidades SI, joules recíprocos, [β β ]=J− − 1{displaystyle [beta]={textrm {J}} {fn}). En unidades no térmicas, también se puede medir en byte por joule, o más convenientemente, gigabyte por nanojoule; 1 K⁻¹ es equivalente a unos 13.062 gigabytes por nanojoule; a temperatura ambiente: T = 300K, β 44 GB/nJ . 39 eV⁻¹ . 2.4×10²⁰ J⁻¹. El factor de conversión es 1 GB/nJ = 8In⁡ ⁡ 2× × 1018{displaystyle 8ln 2times 10^{18} J⁻¹.

Descripción

La beta termodinámica es esencialmente la conexión entre la teoría de la información y la interpretación de la mecánica estadística de un sistema físico a través de su entropía y la termodinámica asociada con su energía. Expresa la respuesta de la entropía a un aumento de energía. Si un sistema se enfrenta a una pequeña cantidad de energía, entonces β describe la cantidad que el sistema aleatorizará.

A través de la definición estadística de temperatura como función de la entropía, la función de frialdad se puede calcular en el conjunto microcanónico a partir de la fórmula

β β =1kBT=1kB()∂ ∂ S∂ ∂ E)V,N{displaystyle beta ={frac {1}{k_{rm {B}T},={frac} {1} {fn}fn}}left({frac {partial S}{partial E}right)_{V,N}

(es decir, el derivado parcial de la entropía S con respecto a la energía E a volumen constante V y número de partículas N).

Ventajas

Aunque totalmente equivalente en contenido conceptual a temperatura, β se considera generalmente una cantidad más fundamental que la temperatura debido al fenómeno de la temperatura negativa, en el que β es continuo ya que cruza cero mientras que T tiene una singularidad.

Además, β tiene la ventaja de ser más fácil de entender causalmente: Si se añade una pequeña cantidad de calor a un sistema, β es el aumento de la entropía dividida por el aumento del calor. La temperatura es difícil de interpretar en el mismo sentido, ya que no es posible "Añadir entropía" a un sistema excepto indirectamente, modificando otras cantidades como temperatura, volumen o número de partículas.

Interpretación estadística

Desde el punto de vista estadístico, β es una cantidad numérica que relaciona dos sistemas macroscópicos en equilibrio. La formulación exacta es la siguiente. Considere dos sistemas, 1 y 2, en contacto térmico, con energías respectivas E₁ y E₂. Suponemos E₁ + E₂ = alguna constante E. El número de microestados de cada sistema se denotará por Ω₁ y Ω₂. Según nuestros supuestos, Ω_i depende sólo de E_i. También suponemos que cualquier microestado del sistema 1 consistente con E₁ puede coexistir con cualquier microestado del sistema 2 consistente con E₂. Por tanto, el número de microestados para el sistema combinado es

Ω Ω =Ω Ω 1()E1)Ω Ω 2()E2)=Ω Ω 1()E1)Ω Ω 2()E− − E1).{displaystyle Omega =Omega _{1}(E_{1})Omega _{2}(E_{2})=Omega _{1}(E_{1})Omega _{2}(E-E_{1}).,}

Deduciremos β del supuesto fundamental de la mecánica estadística:

Cuando el sistema combinado alcanza el equilibrio, se maximiza el número Ω.

(En otras palabras, el sistema busca naturalmente el número máximo de microestados). Por lo tanto, en equilibrio,

ddE1Ω Ω =Ω Ω 2()E2)ddE1Ω Ω 1()E1)+Ω Ω 1()E1)ddE2Ω Ω 2()E2)⋅ ⋅ dE2dE1=0.{fnMicroc} {d}{dE_{1}} Omega =Omega _{2}(E_{2}){frac {d}{dE_{1}} Omega _{1}(E_{1})+Omega _{1}(E_{1}){frac {d}{dE_{2}} Omega _{2}(E_{2})cdot {frac {dE_{2}}=0}

Pero... E₁ + E₂ = E implicación

dE2dE1=− − 1.{fnMicroc} {dE_{2}}=-1.}

Así que

Ω Ω 2()E2)ddE1Ω Ω 1()E1)− − Ω Ω 1()E1)ddE2Ω Ω 2()E2)=0{displaystyle Omega _{2}(E_{2}){frac {d}{dE_{1}} Omega _{1}(E_{1})-Omega _{1}(E_{1}){frac {d}{dE_{2}} Omega...

es decir

ddE1In⁡ ⁡ Ω Ω 1=ddE2In⁡ ⁡ Ω Ω 2en equilibrio.{fnMicroc} {d}{dE_{1}ln} Omega _{1}={frac {d}{dE_{2}ln} Omega _{2}quad {mbox{at equilibrium.}}}}

La relación anterior motiva una definición de β:

β β =dIn⁡ ⁡ Ω Ω dE.{displaystyle beta ={frac {dln # Omega # {dE} #

Conexión de la vista estadística con vista termodinámica

Cuando dos sistemas están en equilibrio, tienen la misma temperatura termodinámica T. Así, intuitivamente, uno esperaría β (como se define a través de microstates) para estar relacionado con T de alguna manera. Este enlace es proporcionado por la suposición fundamental de Boltzmann escrita como

S=kBIn⁡ ⁡ Ω Ω ,{displaystyle S=k_{rm {B}ln Omega}

Donde k_B es la constante de Boltzmann, S es la entropía termodinámica clásica, y Ω es el número de microstates. Así que...

dIn⁡ ⁡ Ω Ω =1kBdS.{displaystyle dln Omega ={frac {1}{k_{rm {B}}dS.}

Sustituir en la definición de β de la definición estadística anterior da

β β =1kBdSdE.{displaystyle beta ={frac {1}{k_{rm {B}} {fnMicroc} {dS} {dE}}

Comparando con la fórmula termodinámica

dSdE=1T,{displaystyle {frac {}{dE}={frac} {1} {T}},}

tenemos

β β =1kBT=1τ τ {displaystyle beta ={frac {1}{k_{rm {B}T}={frac} {1}{tau }}

Donde τ τ {displaystyle tau } se llama temperatura fundamental del sistema, y tiene unidades de energía.