Baricentro
En astronomía, el baricentro (o baricentro; del griego antiguo βαρύς (barús) 'pesado', y κέντρον (kéntron) 'centro') es el centro de masa de dos o más cuerpos que orbitan entre sí y es el punto alrededor del cual orbitan los cuerpos. Un baricentro es un punto dinámico, no un objeto físico. Es un concepto importante en campos como la astronomía y la astrofísica. La distancia desde el centro de masa de un cuerpo hasta el baricentro se puede calcular como un problema de dos cuerpos.
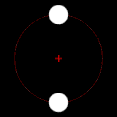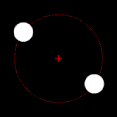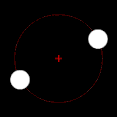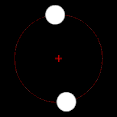
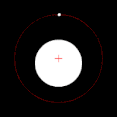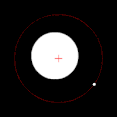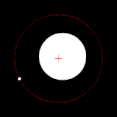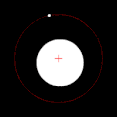
Si uno de los dos cuerpos en órbita es mucho más masivo que el otro y los cuerpos están relativamente cerca uno del otro, el baricentro normalmente se ubicará dentro del objeto más masivo. En este caso, en lugar de que los dos cuerpos parezcan orbitar un punto entre ellos, el cuerpo menos masivo parecerá orbitar alrededor del cuerpo más masivo, mientras que se puede observar que el cuerpo más masivo se tambalea ligeramente. Este es el caso del sistema Tierra-Luna, cuyo baricentro se encuentra en promedio a 4.671 km (2.902 mi) del centro de la Tierra, que es el 75% del radio de la Tierra de 6.378 km (3.963 mi). Cuando los dos cuerpos son de masas similares, el baricentro generalmente se ubicará entre ellos y ambos cuerpos orbitarán alrededor de él. Este es el caso de Plutón y Caronte, uno de los satélites naturales de Plutón, así como de muchos asteroides binarios y estrellas binarias. Cuando el objeto menos masivo está lejos, el baricentro puede ubicarse fuera del objeto más masivo. Este es el caso de Júpiter y el Sol; a pesar de que el Sol es mil veces más masivo que Júpiter, su baricentro está ligeramente fuera del Sol debido a la distancia relativamente grande entre ellos.
En astronomía, las coordenadas baricéntricas son coordenadas no giratorias con origen en el baricentro de dos o más cuerpos. El Sistema Internacional de Referencia Celestial (ICRS) es un sistema de coordenadas baricéntrico centrado en el baricentro del Sistema Solar.
Problema de dos cuerpos
El baricentro es uno de los focos de la órbita elíptica de cada cuerpo. Este es un concepto importante en los campos de la astronomía y la astrofísica. Si a es el semieje mayor del sistema, r1 es el semieje mayor de la órbita principal alrededor el baricentro, y r2 = a − r1 es el semieje mayor de la órbita secundaria. Cuando el baricentro está ubicado dentro del cuerpo más masivo, ese cuerpo parecerá "tambalearse" en lugar de seguir una órbita perceptible. En un caso simple de dos cuerpos, la distancia del centro del primario al baricentro, r1, viene dada por:
- r1=a⋅ ⋅ m2m1+m2=a1+m1m2{displaystyle ¿Qué? {m_{2} {m_{1}+m_{2}}={frac} {f}} {m_}} {m_{2}}}}}}} {f}}} {f}} {f} {f}}} {m_}} {m_}} {m_}}}}} {m_}}}}} {m_}}}}}}}}}} {m_} {m_}}}}}}}} {m_ {m_}}} {m_ {m_}}}}}}}}}}}}}}}}}} {m_ {m_}}} {m_ {m_ {m_ {}}}}}}}}}}}} {m_ {m_ {m_}}}}}}}} {m_ {m_ {m_}}}}}}}}}}}}}} {m_}}} {a}{1+{frac} {m_{1} {m_{2}}}}} {m_{2}}}} {m_}} {}} {m_}}} {m_}}}} {}}}}} {}}} {m_ {}}} {}}}}} {}}}}} {m_} {}}}}}}}} {}}}}}}} {}}} {}}}}}}}}}}}} {}}}}}}} {m}}}}}} {m} {m} {}}}} {} {} {}}} {}}}}}} {}}}}}}}}}}}}}} {}}}}}}}}} {} {}}}}} {} {m}}}}}}}}}} {m}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {
donde:
- r1 es la distancia del centro del cuerpo 1 al barycenter
- a es la distancia entre los centros de los dos cuerpos
- m1 y m2 son las masas de los dos cuerpos.
Ejemplos de primaria y secundaria
La siguiente tabla muestra algunos ejemplos del Sistema Solar. Las cifras se dan redondeadas a tres cifras significativas. Los términos "primario" y "secundaria" se utilizan para distinguir entre los participantes involucrados, siendo el más grande el principal y el más pequeño el secundario.
- m1 es la masa de la primaria en las masas terrestres (MEarth)
- m2 es la masa de la secundaria en las masas terrestres (MEarth)
- a (km) es la distancia orbital promedio entre los centros de los dos cuerpos
- r1 (km) es la distancia desde el centro de la primaria al barycenter
- R1 (km) es el radio de la primaria
- r1/R1 un valor inferior a uno significa que el barycenter se encuentra dentro de la primaria
| Primaria | m1 (Miedo) | Secundaria | m2 ()MTierra) | a (km) | r1 (km) | R1 (km) | r1/R1 |
|---|---|---|---|---|---|---|---|
| Tierra | 1 | Luna | 0,0123 | 384.000 | 4.670 | 6.380 | 0.732 |
| Plutón | 0,0021 | Charon | 0,000254 (0.121 M♇) | 19.600 | 2.110 | 1.150 | 1.83 |
| Sol | 333.000 | Tierra | 1 | 150,000,000 (1 UA) | 449 | 696.000 | 0,000646 |
| Sol | 333.000 | Júpiter | 318 (0.000955 M☉) | 778,000,000 (5.20 UA) | 742.000 | 696.000 | 1.07 |
| Sol | 333.000 | Saturno | 95.2 | 1.430 millones (9.58 AU) | 409.000 | 696.000 | 0.588 |
- ^ La Tierra tiene una "bomba" perceptible. También vea mareas.
- ^ Plutón y Charon son a veces considerados un sistema binario porque su barycenter no miente dentro de cualquier cuerpo.
- ^ La oscilación del Sol apenas es perceptible.
- ^ El Sol orbita un barycenter justo encima de su superficie.
Ejemplo con el Sol
Si m1 ≫ m2— lo cual es cierto para el Sol y cualquier planeta, entonces la proporción r1/R1 se aproxima a:
- aR1⋅ ⋅ m2m1.{displaystyle {frac {f} {cdot}cdot} {fnMicroc {m_{2} {m_{1}}}
Por lo tanto, el baricentro del sistema Sol-planeta estará fuera del Sol solo si:
- 1;Rightarrow ;{acdot m_{mathrm {planet} }}>{R_{odot }cdot m_{odot }}approx 2.3times 10^{11};m_{oplus };{mbox{km}}approx 1530;m_{oplus };{mbox{AU}}}" xmlns="http://www.w3.org/1998/Math/MathML">aR⊙ ⊙ ⋅ ⋅ mplanetm⊙ ⊙ ■1⇒ ⇒ a⋅ ⋅ mplanet■R⊙ ⊙ ⋅ ⋅ m⊙ ⊙ .. 2.3× × 1011m⊕ ⊕ km.. 1530m⊕ ⊕ AU{displaystyle {a over R_{odot}cdot {m_{mathrm {planet} over m_{odot }}] 1;Rightarrow ;{acdot m_{mathrm {planet} } {R_{odot}cdot m_{odot}approx 2.3times 10^{11};m_{oplus };{mbox{km}approx 1530;m_{oplus };{mbox {AU}}
1;Rightarrow ;{acdot m_{mathrm {planet} }}>{R_{odot }cdot m_{odot }}approx 2.3times 10^{11};m_{oplus };{mbox{km}}approx 1530;m_{oplus };{mbox{AU}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5e614dfeb2c3a2d4db0adc0858f82e78557ea6a7" style="vertical-align: -2.338ex; width:80.996ex; height:5.509ex;"/>
—es decir, donde el planeta es masivo y lejos del Sol.
Si Júpiter tuviera la órbita de Mercurio (57 900 000 km, 0,387 UA), el baricentro Sol-Júpiter estaría aproximadamente a 55 000 km del centro del Sol (r1/R1 ≈ 0,08). Pero incluso si la Tierra tuviera la órbita de Eris (1,02×1010 km, 68 AU), el Sol... El baricentro de la Tierra todavía estaría dentro del Sol (a poco más de 30 000 km del centro).
Para calcular el movimiento real del Sol, solo se deben considerar los movimientos de los cuatro planetas gigantes (Júpiter, Saturno, Urano, Neptuno). Las contribuciones de todos los demás planetas, planetas enanos, etc. son insignificantes. Si los cuatro planetas gigantes estuvieran en línea recta en el mismo lado del Sol, el centro de masa combinado se encontraría a aproximadamente 1,17 radios solares, o un poco más de 810 000 km sobre la superficie del Sol.
Los cálculos anteriores se basan en la distancia media entre los cuerpos y arrojan el valor medio r1. Pero todas las órbitas celestes son elípticas, y la distancia entre los cuerpos varía entre los ábsides, dependiendo de la excentricidad, e. Por lo tanto, la posición del baricentro también varía, y es posible que en algunos sistemas el baricentro esté a veces dentro ya veces fuera del cuerpo más masivo. Esto ocurre donde
- {frac {r_{1}}{R_{1}}}>{frac {1}{1+e}}.}" xmlns="http://www.w3.org/1998/Math/MathML">11− − e■r1R1■11+e.{fnMicroc} {1}{1-e} {frac} {fn} {fn}} {fnK}} {fnK}}} {fnh}}} {fn}}} {fn}}}} {fnK}}}}} {fnf}}}}}}} {f}} {f}}}}} {fn}}}}}}}} {f}}}}}}}}} {f}}}}}}}}} {f}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}} {f} {f} {f}}f}}}}f}}}}}}f}}}f} {f} {f} {f} {f} {f}f}f}f}f}f}f}}}f} {1}{1+e}}
{frac {r_{1}}{R_{1}}}>{frac {1}{1+e}}.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/88b67fac6c6b130c3f7482089a14e3d0bb76fd47" style="vertical-align: -2.171ex; width:22.343ex; height:5.509ex;"/>
El sistema Sol-Júpiter, con eJúpiter = 0,0484, simplemente no califica: 1,05 < 1,07 > 0,954.
Correcciones relativistas
En la mecánica clásica (gravitación newtoniana), esta definición simplifica los cálculos y no presenta problemas conocidos. En la relatividad general (gravitación einsteiniana), surgen complicaciones porque, si bien es posible, dentro de aproximaciones razonables, definir el baricentro, encontramos que el sistema de coordenadas asociado no refleja completamente la desigualdad de frecuencias de reloj en diferentes ubicaciones. Brumberg explica cómo establecer coordenadas baricéntricas en relatividad general.
Los sistemas de coordenadas implican un tiempo mundial, es decir, una coordenada de tiempo global que podría configurarse mediante telemetría. Los relojes individuales de construcción similar no estarán de acuerdo con este estándar, porque están sujetos a diferentes potenciales gravitacionales o se mueven a varias velocidades, por lo que el tiempo mundial debe estar sincronizado con algún reloj ideal que se supone que está muy lejos de todo el autocontrol. sistema gravitatorio. Este estándar de tiempo se denomina tiempo de coordenadas baricéntricas (TCB, sic).
Elementos orbitales baricéntricos seleccionados
Los elementos orbitales osculadores baricéntricos de algunos objetos del Sistema Solar son los siguientes:
| Objeto | Axis semi-major (en UA) | Apoapsis (en UA) | Período orbital (en años) |
|---|---|---|---|
| C/2006 P1 (McNaught) | 2.050 | 4,100 | 92.600 |
| C/1996 B2 (Hyakutake) | 1.700 | 3.410 | 70.000 |
| C/2006 M4 (SWAN) | 1.300 | 2.600 | 47.000 |
| (308933) 2006 SQ372 | 799 | 1.570 | 22.600 |
| (87269) 2000 OO67 | 549 | 1.078 | 12.800 |
| 90377 Sedna | 506 | 937 | 11.400 |
| 2007 TG422 | 501 | 967 | 11.200 |
Para objetos con una excentricidad tan alta, las coordenadas baricéntricas son más estables que las coordenadas heliocéntricas para una época determinada porque la órbita oscilante baricéntrica no se ve tan afectada por el lugar en el que se encuentra Júpiter en su órbita de 11,8 años.
Contenido relacionado
CFG
Edulcorante
Intercambiabilidad