B-spline racional no uniforme

La spline de base racional no uniforme (NURBS) es un modelo matemático que utiliza splines de base (B-splines) que se usa comúnmente en gráficos por computadora para representar curvas y superficies.. Ofrece una gran flexibilidad y precisión para manejar tanto formas analíticas (definidas por fórmulas matemáticas comunes) como modeladas. Es un tipo de modelado de curvas, a diferencia del modelado poligonal o la escultura digital. Las curvas NURBS se utilizan comúnmente en el diseño asistido por computadora (CAD), la fabricación (CAM) y la ingeniería (CAE). Forman parte de numerosos estándares de toda la industria, como IGES, STEP, ACIS y PHIGS. Las herramientas para crear y editar superficies NURBS se encuentran en varios paquetes de software de animación y gráficos 3D.

Pueden ser manejados de manera eficiente por programas de computadora pero permiten una fácil interacción humana. Las superficies NURBS son funciones de dos parámetros que se asignan a una superficie en un espacio tridimensional. La forma de la superficie está determinada por los puntos de control. En una forma compacta, las superficies NURBS pueden representar formas geométricas simples. Para formas orgánicas complejas, las T-splines y las superficies de subdivisión son más adecuadas porque reducen a la mitad el número de puntos de control en comparación con las superficies NURBS.

En general, la edición de curvas y superficies NURBS es intuitiva y predecible. Los puntos de control siempre están conectados directamente a la curva o superficie, o actúan como si estuvieran conectados por una banda elástica. Dependiendo del tipo de interfaz de usuario, la edición de curvas y superficies NURBS puede realizarse a través de sus puntos de control (similares a las curvas de Bézier) o a través de herramientas de nivel superior como modelado de spline y edición jerárquica.

Antecedentes históricos

Antes de las computadoras, los diseños se dibujaban a mano en papel con varias herramientas de dibujo. Se usaron reglas para líneas rectas, compases para círculos y transportadores para ángulos. Pero muchas formas, como la curva de forma libre de la proa de un barco, no se pudieron dibujar con estas herramientas. Aunque tales curvas se podían dibujar a mano alzada en el tablero de dibujo, los constructores navales a menudo necesitaban una versión de tamaño natural que no se podía hacer a mano. Dibujos tan grandes se hicieron con la ayuda de tiras flexibles de madera, llamadas splines. Las estrías se mantuvieron en su lugar en una serie de puntos predeterminados, llamados "patos" (que estaban hechos de plomo y 3 pulgadas de largo. El 'pico' del 'pato' empujó contra la ranura: los viejos libros de diseño de yates asumieron estos métodos); entre los patos, la elasticidad del material estriado hizo que la tira tomara la forma que minimizaba la energía de la flexión, creando así la forma más suave posible que se ajustaba a las restricciones. La forma se podía ajustar moviendo los patos.

En 1946, los matemáticos comenzaron a estudiar la forma spline y derivaron la fórmula polinomial por partes conocida como curva spline o función spline. IJ Schoenberg le dio a la función spline su nombre por su parecido con la spline mecánica utilizada por los dibujantes.

A medida que se introdujeron las computadoras en el proceso de diseño, se investigaron las propiedades físicas de tales splines para que pudieran modelarse con precisión matemática y reproducirse donde fuera necesario. El trabajo pionero fue realizado en Francia por el ingeniero de Renault, Pierre Bézier, y el físico y matemático de Citroën, Paul de Casteljau. Trabajaron casi en paralelo, pero debido a que Bézier publicó los resultados de su trabajo, las curvas de Bézier recibieron su nombre, mientras que el nombre de De Casteljau solo se asocia con algoritmos relacionados.

Al principio, NURBS solo se usaba en los paquetes CAD patentados de las empresas automotrices. Más tarde se convirtieron en parte de los paquetes estándar de gráficos por computadora.

La representación interactiva en tiempo real de curvas y superficies NURBS estuvo disponible comercialmente por primera vez en estaciones de trabajo de Silicon Graphics en 1989. En 1993, CAS Berlin, una pequeña empresa emergente, desarrolló el primer modelador NURBS interactivo para PC, llamado NöRBS. en cooperación con la Universidad Técnica de Berlín.

Continuidad

Una superficie en construcción, p. el casco de un yate a motor, suele estar compuesto por varias superficies NURBS conocidas como parches NURBS (o simplemente parches). Estos parches de superficie deben encajarse de tal manera que los límites sean invisibles. Esto se expresa matemáticamente mediante el concepto de continuidad geométrica.

Existen herramientas de nivel superior que se benefician de la capacidad de NURBS para crear y establecer continuidad geométrica de diferentes niveles:

• Continuidad de la posición (G⁰) sostiene cada vez que las posiciones finales de dos curvas o superficies coinciden. Las curvas o superficies todavía pueden encontrarse en un ángulo, dando lugar a un ángulo o borde afilado y causando puntos de interés rotos.
• Continencia tripartita (G1) requiere que los vectores finales de las curvas o superficies sean paralelos y señalen de la misma manera, descartando bordes agudos. Debido a que los puntos destacados que caen en un borde tangencialmente continuo son siempre continuos y por lo tanto parecen naturales, este nivel de continuidad puede ser suficiente.
• Continuidad de la curvatura (G2) requiere además que los vectores finales sean de la misma longitud y tasa de cambio de longitud. Los relieves que caen en un borde contínuo de curvatura no muestran ningún cambio, causando que las dos superficies aparezcan como una. Esto se puede reconocer visualmente como "perfectamente suave". Este nivel de continuidad es muy útil en la creación de modelos que requieren muchos parches bi-cubicos que componen una superficie continua.

La continuidad geométrica se refiere principalmente a la forma de la superficie resultante; dado que las superficies NURBS son funciones, también es posible analizar las derivadas de la superficie con respecto a los parámetros. Esto se conoce como continuidad paramétrica. La continuidad paramétrica de un grado dado implica la continuidad geométrica de ese grado.

La continuidad paramétrica de primer y segundo nivel (C⁰ y C¹) es, a efectos prácticos, idéntica a la continuidad posicional y tangencial (G⁰ y G¹). La continuidad paramétrica de tercer nivel (C²), sin embargo, difiere de la continuidad de curvatura en que su parametrización también es continua. En la práctica, la continuidad C² es más fácil de lograr si se utilizan B-splines uniformes.

La definición de Cⁿ continuidad requiere que nderivado de curvas/superficies adyacentes (dnC()u)/dun{displaystyle d^{n}C(u)/du^{n}) son iguales en un conjunto. Tenga en cuenta que los derivados (partiales) de curvas y superficies son vectores que tienen una dirección y una magnitud; ambos deben ser iguales.

Los toques de luz y los reflejos pueden revelar el suavizado perfecto, que de otro modo sería prácticamente imposible de lograr sin superficies NURBS que tengan al menos una continuidad G². Este mismo principio se utiliza como uno de los métodos de evaluación de superficies mediante el cual una imagen de trazado de rayos o mapeada de reflexión de una superficie con rayas blancas que se reflejan en ella mostrará incluso las desviaciones más pequeñas en una superficie o conjunto de superficies. Este método se deriva de la creación de prototipos de automóviles en los que se inspecciona la calidad de la superficie comprobando la calidad de los reflejos de un techo de luz de neón en la superficie del automóvil. Este método también se conoce como "Análisis cebra".

Especificaciones técnicas

Una curva NURBS se define por su orden, un conjunto de puntos de control ponderados y un vector de nudo. Las curvas y superficies de NURBS son generalizaciones tanto de B-splines como de Bézier curvas y superficies, la diferencia principal es el peso de los puntos de control, lo que hace curvas NURBS racional. ()Non-rational, aka simple, B-splines son un caso especial / subconjunto de líneas B racionales, donde cada punto de control es una coordinación regular no homógena [no 'w'] en lugar de una coordenadas homogénea. Eso equivale a tener peso "1" en cada punto de control; Racional Las líneas B utilizan el 'w' de cada punto de control como un peso.) Mediante el uso de una cuadrícula bidimensional de puntos de control, se pueden crear superficies NURBS incluyendo parches plano y secciones de esferas. Estas son parametrizadas con dos variables (normalmente llamadas s y t o u y v). Esto se puede ampliar a dimensiones arbitrarias para crear cartografía NURBS Rn→ → Rn{displaystyle mathbb {R}n}to mathbb {R} {fn}.

Las curvas y superficies NURBS son útiles por varias razones:

• El conjunto de NURBS para un pedido dado es invariante bajo transformaciones de afina: operaciones como rotaciones y traducciones se pueden aplicar a curvas y superficies NURBS aplicando a sus puntos de control.
• Ofrecen una forma matemática común para ambas formas analíticas estándar (por ejemplo, conics) y de forma libre.
• Proporcionan la flexibilidad para diseñar una gran variedad de formas.
• Reducen el consumo de memoria al almacenar formas (comparados a métodos más simples).
• Pueden ser evaluados razonablemente rápidamente por algoritmos numéricos y precisos.

Aquí, NURBS se analiza principalmente en una dimensión (curvas); se puede generalizar a dos (superficies) o incluso a más dimensiones.

Orden

El orden de una curva NURBS define el número de puntos de control cercanos que influyen en cualquier punto de la curva. La curva se representa matemáticamente por un polinomio de grado uno menor que el orden de la curva. Por lo tanto, las curvas de segundo orden (que están representadas por polinomios lineales) se denominan curvas lineales, las curvas de tercer orden se denominan curvas cuadráticas y las curvas de cuarto orden se denominan curvas cúbicas. El número de puntos de control debe ser mayor o igual al orden de la curva.

En la práctica, las curvas cúbicas son las más utilizadas. Las curvas de quinto y sexto orden son a veces útiles, especialmente para obtener derivadas continuas de orden superior, pero las curvas de orden superior prácticamente nunca se usan porque conducen a problemas numéricos internos y tienden a requerir tiempos de cálculo desproporcionadamente largos.

Puntos de control

Los puntos de control determinan la forma de la curva. Por lo general, cada punto de la curva se calcula tomando una suma ponderada de varios puntos de control. El peso de cada punto varía según el parámetro rector. Para una curva de grado d, el peso de cualquier punto de control solo es distinto de cero en los intervalos d+1 del espacio de parámetros. Dentro de esos intervalos, el peso cambia según una función polinomial (funciones base) de grado d. En los límites de los intervalos, las funciones de base van suavemente a cero, la suavidad está determinada por el grado del polinomio.

Como ejemplo, la función base de grado uno es una función triangular. Se eleva de cero a uno, luego vuelve a caer a cero. Mientras sube, la función base del punto de control anterior cae. De esa forma, la curva se interpola entre los dos puntos, y la curva resultante es un polígono, que es continuo, pero no diferenciable en los límites del intervalo, o nudos. Los polinomios de mayor grado tienen correspondientemente más derivadas continuas. Tenga en cuenta que dentro del intervalo, la naturaleza polinómica de las funciones base y la linealidad de la construcción hacen que la curva sea perfectamente suave, por lo que solo en los nudos puede surgir la discontinuidad.

En muchas aplicaciones, el hecho de que un único punto de control solo influya en aquellos intervalos en los que está activo es una propiedad muy deseable, conocida como soporte local. En el modelado, permite cambiar una parte de una superficie manteniendo otras partes sin cambios.

Agregar más puntos de control permite una mejor aproximación a una curva determinada, aunque solo una determinada clase de curvas se puede representar exactamente con un número finito de puntos de control. Las curvas NURBS también presentan un peso escalar para cada punto de control. Esto permite un mayor control sobre la forma de la curva sin aumentar indebidamente el número de puntos de control. En particular, agrega secciones cónicas como círculos y elipses al conjunto de curvas que se pueden representar exactamente. El término racional en NURBS se refiere a estos pesos.

Los puntos de control pueden tener cualquier dimensionalidad. Los puntos unidimensionales simplemente definen una función escalar del parámetro. Estos se utilizan normalmente en programas de procesamiento de imágenes para ajustar el brillo y las curvas de color. Los puntos de control tridimensionales se usan abundantemente en el modelado 3D, donde se usan en el significado cotidiano de la palabra 'punto', una ubicación en el espacio 3D. Los puntos multidimensionales pueden usarse para controlar conjuntos de valores controlados por el tiempo, p. los diferentes ajustes de posición y rotación de un brazo robótico. Las superficies NURBS son solo una aplicación de esto. Cada 'punto' de control es en realidad un vector completo de puntos de control, que define una curva. Estas curvas comparten su grado y el número de puntos de control y abarcan una dimensión del espacio de parámetros. Al interpolar estos vectores de control sobre la otra dimensión del espacio de parámetros, se obtiene un conjunto continuo de curvas que definen la superficie.

Vector de nudo

El vector de nudo es una secuencia de valores de parámetros que determina dónde y cómo afectan los puntos de control a la curva NURBS. El número de nudos siempre es igual al número de puntos de control más el grado de la curva más uno (es decir, el número de puntos de control más el orden de la curva). El vector de nudos divide el espacio paramétrico en los intervalos mencionados anteriormente, generalmente denominados tramos de nudos. Cada vez que el valor del parámetro ingresa en un nuevo intervalo de nudos, se activa un nuevo punto de control, mientras que se descarta un punto de control anterior. De ello se deduce que los valores en el vector nudo deben estar en orden no decreciente, por lo que (0, 0, 1, 2, 3, 3) es válido mientras que (0, 0, 2, 1, 3, 3) no lo es.

Los nudos consecutivos pueden tener el mismo valor. Esto define entonces un intervalo de nudos de longitud cero, lo que implica que dos puntos de control se activan al mismo tiempo (y, por supuesto, dos puntos de control se desactivan). Esto repercute en la continuidad de la curva resultante o de sus derivadas superiores; por ejemplo, permite la creación de esquinas en una curva NURBS suave. Un número de nudos coincidentes a veces se denomina nudo con cierta multiplicidad. Los nudos con multiplicidad dos o tres se conocen como nudos dobles o triples. La multiplicidad de un nudo se limita al grado de la curva; ya que una mayor multiplicidad dividiría la curva en partes inconexas y dejaría puntos de control sin usar. Para NURBS de primer grado, cada nodo se empareja con un punto de control.

El vector de nudo generalmente comienza con un nudo que tiene una multiplicidad igual al orden. Esto tiene sentido, ya que activa los puntos de control que tienen influencia en el tramo del primer nudo. De manera similar, el vector de nudos suele terminar con un nudo de esa multiplicidad. Las curvas con tales vectores de nudo comienzan y terminan en un punto de control.

Los valores de los nodos controlan el mapeo entre el parámetro de entrada y el valor NURBS correspondiente. Por ejemplo, si una NURBS describe una ruta a través del espacio a lo largo del tiempo, los nudos controlan el tiempo que la función pasa por los puntos de control. Sin embargo, a los efectos de representar formas, solo importan las proporciones de la diferencia entre los valores de los nudos; en ese caso, los vectores nudo (0, 0, 1, 2, 3, 3) y (0, 0, 2, 4, 6, 6) producen la misma curva. Las posiciones de los valores de los nudos influyen en la asignación del espacio de parámetros al espacio de curvas. La representación de una curva NURBS generalmente se realiza avanzando con un paso fijo a través del rango del parámetro. Al cambiar las longitudes de tramo de nudo, se pueden usar más puntos de muestra en regiones donde la curvatura es alta. Otro uso es en situaciones en las que el valor del parámetro tiene algún significado físico, por ejemplo, si el parámetro es el tiempo y la curva describe el movimiento de un brazo robótico. Las longitudes de los nudos se traducen luego en velocidad y aceleración, que son esenciales para evitar daños en el brazo robótico o su entorno. Esta flexibilidad en el mapeo es a lo que se refiere la frase no uniforme en NURBS.

Necesarios solo para cálculos internos, los nudos generalmente no son útiles para los usuarios de software de modelado. Por lo tanto, muchas aplicaciones de modelado no hacen que los nudos sean editables o incluso visibles. Por lo general, es posible establecer vectores de nudos razonables observando la variación en los puntos de control. Las versiones más recientes del software NURBS (p. ej., Autodesk Maya y Rhinoceros 3D) permiten la edición interactiva de las posiciones de los nudos, pero esto es significativamente menos intuitivo que la edición de los puntos de control.

Construcción de las funciones base

Las funciones de base B-spline utilizadas en la construcción de curvas NURBS generalmente se denotan como Ni,n()u){displaystyle N_{i,n}(u)}, en que i{displaystyle i} corresponde a i{displaystyle i}^Tpunto de control, y n{displaystyle n} corresponde al grado de la función de base. La dependencia del parámetro se deja a menudo fuera, así que podemos escribir Ni,n{displaystyle N_{i,n}. La definición de estas funciones de base es recurrente en n{displaystyle n}. Funciones de grado-0 Ni,0{displaystyle N_{i,0} son funciones constantes. Son uno en el nudo correspondiente y cero en todas partes. Efectivamente, Ni,n{displaystyle N_{i,n} es una interpolación lineal Ni,n− − 1{displaystyle N_{i,n-1} y Ni+1,n− − 1{displaystyle N_{i+1,n-1}. Las dos últimas funciones no son cero para n{displaystyle n} nudos, superpuestos para n− − 1{displaystyle n-1} nudos. La función Ni,n{displaystyle N_{i,n} es calculado como

Ni,n=fi,nNi,n− − 1+gi,nNi+1,n− − 1{displaystyle N_{i,n}=f_{i,n}N_{i,n-1}+g_{i,n}N_{i+1,n-1}

fi{displaystyle F_{i} se eleva linealmente de cero a uno en el intervalo donde Ni,n− − 1{displaystyle N_{i,n-1} no es cero, mientras gi+1{displaystyle G_{i+1} cae de uno a cero en el intervalo donde Ni+1,n− − 1{displaystyle N_{i+1,n-1} no es cero. Como se mencionó anteriormente, Ni,1{displaystyle N_{i,1} es una función triangular, no cero sobre dos nudos que crecen de cero a uno en el primero, y cayendo a cero en el segundo nudo. Las funciones de base de orden superior no son cero sobre los intervalos de nudos correspondientes y tienen un grado correspondientemente mayor. Si u{displaystyle u} es el parámetro, y ki{displaystyle K_{i} es i{displaystyle i}^T nudo, podemos escribir las funciones f{displaystyle f} y g{displaystyle g} como

fi,n()u)=u− − kiki+n− − ki{displaystyle f_{i,n}(u)={u-k_{i} {fn}}

y

gi,n()u)=1− − fi,n()u)=ki+n− − uki+n− − ki{displaystyle g_{i,n}(u)=1-f_{i,n}(u)={k_{i+n}-u} {fn}}

Funciones f{displaystyle f} y g{displaystyle g} son positivos cuando las funciones de base de orden inferior correspondientes no son cero. Por inducción en n sigue que las funciones de base no son negativas para todos los valores de n{displaystyle n} y u{displaystyle u}. Esto hace que el cálculo de las funciones de base sea numéricamente estable.

Nuevamente por inducción, se puede probar que la suma de las funciones base para un valor particular del parámetro es la unidad. Esto se conoce como la propiedad partición de la unidad de las funciones base.

Las figuras muestran las funciones de base lineal y cuadrática para los nudos {..., 0, 1, 2, 3, 4, 4.1, 5.1, 6.1, 7.1,...}

La duración de un nudo es considerablemente más corta que la de los demás. En ese intervalo de nudos, el pico en la función de base cuadrática es más claro, alcanzando casi uno. Por el contrario, las funciones de base contiguas se reducen a cero más rápidamente. En la interpretación geométrica, esto significa que la curva se aproxima mucho al punto de control correspondiente. En el caso de un nudo doble, la longitud del tramo del nudo se vuelve cero y el pico alcanza exactamente uno. La función base ya no es diferenciable en ese punto. La curva tendrá una esquina pronunciada si los puntos de control vecinos no son colineales.

Forma general de una curva NURBS

Utilizando las definiciones de las funciones de base Ni,n{displaystyle N_{i,n} del párrafo anterior, una curva NURBS toma la siguiente forma:

C()u)=.. i=1kNi,n()u)wi.. j=1kNj,n()u)wjPi=.. i=1kNi,n()u)wiPi.. i=1kNi,n()u)wi{displaystyle C(u)=sum ¿Por qué? {N_{i,n}(u)w_{i}{sum ¿Qué? {fnMicroc} {fnK} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} ¿Qué? {fnK} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft}}} {fn}} {fnMicrosoft}}} {fnK}}}}}}} {fnK}}}} {f}}} {f}}}}} {f}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}} {f} {f}}}}}}}}}}}}}}}} {f}}}} {f}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}} {f}}} {f}}}}} {f}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}} ¿Qué?

En esto, k{displaystyle k} es el número de puntos de control Pi{displaystyle mathbf {} _{i} y wi{displaystyle ¿Qué? son los pesos correspondientes. El denominador es un factor normalizador que evalúa a uno si todos los pesos son uno. Esto se puede ver desde la partición de propiedad de unidad de las funciones de base. Es costumbre escribir esto como

C()u)=.. i=1kRi,n()u)Pi{displaystyle C(u)=sum ¿Qué?

en el que las funciones

Ri,n()u)=Ni,n()u)wi.. j=1kNj,n()u)wj{displaystyle R_{i,n}(u)={N_{i,n}(u)w_{i} over sum _{j=1}{k}N_{j,n}(u)w_{j}}}}

are known as the rational basis functions

Forma general de una superficie NURBS

Una superficie NURBS se obtiene como el producto tensor de dos curvas NURBS, utilizando así dos parámetros independientes u{displaystyle u} y v{displaystyle v} (con índices i{displaystyle i} y j{displaystyle j} respectivamente:

S()u,v)=.. i=1k.. j=1lRi,j()u,v)Pi,j{displaystyle S(u,v)=sum ¿Por qué?

con

Ri,j()u,v)=Ni,n()u)Nj,m()v)wi,j.. p=1k.. q=1lNp,n()u)Nq,m()v)wp,q{displaystyle R_{i,j}(u,v)={frac {N_{i,n}(u)N_{j,m}(v)w_{i,j}{sum - ¿Qué? ¿Qué?

como funciones de base racional.

Manipulación de objetos NURBS

Se pueden aplicar varias transformaciones a un objeto NURBS. Por ejemplo, si alguna curva se define usando un cierto grado y N puntos de control, la misma curva se puede expresar usando el mismo grado y N+1 puntos de control. En el proceso, varios puntos de control cambian de posición y se inserta un nudo en el vector de nudo. Estas manipulaciones se utilizan ampliamente durante el diseño interactivo. Al agregar un punto de control, la forma de la curva debe permanecer igual, formando el punto de partida para ajustes posteriores. Algunas de estas operaciones se analizan a continuación.

Inserción de nudos

Como sugiere el término, inserción nudo inserta un nudo en el vector del nudo. Si el grado de la curva es n{displaystyle n}, entonces n− − 1{displaystyle n-1} puntos de control reemplazados por n{displaystyle n} nuevas. La forma de la curva permanece igual.

Un nudo se puede insertar varias veces, hasta la multiplicidad máxima del nudo. Esto a veces se denomina refinamiento de nudos y se puede lograr mediante un algoritmo que es más eficiente que la inserción repetida de nudos.

Eliminación de nudos

La eliminación de nudos es lo contrario de la inserción de nudos. Su propósito es eliminar los nudos y los puntos de control asociados para obtener una representación más compacta. Obviamente, esto no siempre es posible manteniendo la forma exacta de la curva. En la práctica, se utiliza una tolerancia en la precisión para determinar si se puede eliminar un nudo. El proceso se utiliza para limpiar después de una sesión interactiva en la que los puntos de control pueden haberse agregado manualmente o después de importar una curva de una representación diferente, donde un proceso de conversión sencillo conduce a puntos de control redundantes.

Elevación de grados

Una curva NURBS de un grado particular siempre se puede representar mediante una curva NURBS de mayor grado. Esto se usa con frecuencia cuando se combinan curvas NURBS separadas, por ejemplo, al crear una superficie NURBS interpolando entre un conjunto de curvas NURBS o al unificar curvas adyacentes. En el proceso, las diferentes curvas deben llevarse al mismo grado, generalmente el grado máximo del conjunto de curvas. El proceso se conoce como grado de elevación.

Curvatura

La propiedad más importante en geometría diferencial es la curvatura κ κ {displaystyle kappa }. Describe las propiedades locales (edges, esquinas, etc.) y las relaciones entre el primero y segundo derivado, y por lo tanto, la forma curva precisa. Habiendo determinado los derivados es fácil calcular κ κ =Silencior.()t)× × r.()t)SilencioSilencior.()t)Silencio3{displaystyle kappa ={frac}}}} o aproximado como la arclength del segundo derivado κ κ =Silencior.()so)Silencio{displaystyle kappa = perpetuar'(s_{o}). El cálculo directo de la curvatura κ κ {displaystyle kappa } con estas ecuaciones es la gran ventaja de curvas parametizadas contra sus representaciones poligonales.

Ejemplo: un círculo

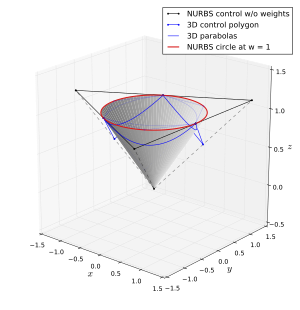
Las splines no racionales o las curvas de Bézier pueden aproximarse a un círculo, pero no pueden representarlo exactamente. Los splines racionales pueden representar exactamente cualquier sección cónica, incluido el círculo. Esta representación no es única, pero una posibilidad aparece a continuación:

x	Sí.	z	Peso
1	0	0	1
1	1	0	22{displaystyle scriptstyle {frac {sqrt {2}{2}}} {2}}}}} {2}}}}}}}}} {c}}}}}}}}} {}}}}}}}}}}}}}} {}}} {}}}}}}}}}}}} {}}} {}}}}}}}}} {}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {} {}}}}}} {}}}}}}}}}}}}} {}}}}} {}}}}}}}}}}}}}}}} {}}}}}}} {}}}}}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}
0	1	0	1
-1	1	0	22{displaystyle scriptstyle {frac {sqrt {2}{2}}} {2}}}}} {2}}}}}}}}} {c}}}}}}}}} {}}}}}}}}}}}}}} {}}} {}}}}}}}}}}}} {}}} {}}}}}}}}} {}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {} {}}}}}} {}}}}}}}}}}}}} {}}}}} {}}}}}}}}}}}}}}}} {}}}}}}} {}}}}}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}
-1	0	0	1
-1	-1	0	22{displaystyle scriptstyle {frac {sqrt {2}{2}}} {2}}}}} {2}}}}}}}}} {c}}}}}}}}} {}}}}}}}}}}}}}} {}}} {}}}}}}}}}}}} {}}} {}}}}}}}}} {}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {} {}}}}}} {}}}}}}}}}}}}} {}}}}} {}}}}}}}}}}}}}}}} {}}}}}}} {}}}}}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}
0	-1	0	1
1	-1	0	22{displaystyle scriptstyle {frac {sqrt {2}{2}}} {2}}}}} {2}}}}}}}}} {c}}}}}}}}} {}}}}}}}}}}}}}} {}}} {}}}}}}}}}}}} {}}} {}}}}}}}}} {}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {} {}}}}}} {}}}}}}}}}}}}} {}}}}} {}}}}}}}}}}}}}}}} {}}}}}}} {}}}}}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}
1	0	0	1

El orden es tres, ya que un círculo es una curva cuadrática y el orden de la espinilla es uno más que el grado de sus segmentos polinomios en sentido parcial. El vector nudo es {}0,0,0,π π /2,π π /2,π π ,π π ,3π π /2,3π π /2,2π π ,2π π ,2π π }{displaystyle {0,0,0,pi /2,pi /2,pipi3pi3pi /2,3pi /2,2pi2pi2pi2pi2pi2 #. El círculo se compone de cuatro círculos trimestrales, unidos con nudos dobles. Aunque los nudos dobles en una curva NURBS de tercer orden normalmente resultarían en la pérdida de continuidad en el primer derivado, los puntos de control se posicionan de tal manera que el primer derivado es continuo. De hecho, la curva es infinitamente diferente en todas partes, como debe ser si representa exactamente un círculo.

La curva representa un círculo exactamente, pero no está exactamente parametrizada en la longitud del arco del círculo. Esto significa, por ejemplo, que el punto en t{displaystyle t} no miente ()pecado⁡ ⁡ ()t),#⁡ ⁡ ()t)){displaystyle (sin(t),cos(t)} (excepto el punto de inicio, medio y final de cada círculo trimestral, ya que la representación es simétrica). Esto sería imposible, ya que x coordinación del círculo proporcionaría una expresión polinómica racional exacta #⁡ ⁡ ()t){displaystyle cos(t)}, que es imposible. El círculo hace una revolución completa como su parámetro t{displaystyle t} va de 0 a 0 2π π {displaystyle 2pi}, pero esto es sólo porque el vector nudo fue elegido arbitrariamente como múltiplos de π π /2{displaystyle pi /2}.