Aversión al riesgo

Aversión de riesgo (rojo) contrastada con la neutralidad de riesgo (amarillo) y amor de riesgo (orange) en diferentes entornos. Gráfico izquierdo: Una función de utilidad aversa de riesgo es concave (desde abajo), mientras que una función de utilidad amorosa de riesgo es convex. Gráfico medio: En el espacio de valor estándar, las curvas de indiferencia aversa de riesgo se inclinan hacia arriba. Gráfico derecho: Con probabilidades fijas de dos estados alternativos 1 y 2, las curvas de indiferencia aversa de riesgo sobre pares de resultados contingentes del estado son convexas.

En economía y finanzas, la aversión al riesgo es la tendencia de las personas a preferir resultados con baja incertidumbre a aquellos resultados con alta incertidumbre, incluso si el resultado promedio de estos últimos es igual o mayor en términos monetarios. valor que el resultado más cierto. La aversión al riesgo explica la inclinación a aceptar una situación con un pago más predecible, pero posiblemente más bajo, en lugar de otra situación con un pago altamente impredecible, pero posiblemente más alto. Por ejemplo, un inversionista adverso al riesgo podría optar por poner su dinero en una cuenta bancaria con una tasa de interés baja pero garantizada, en lugar de una acción que puede tener altos rendimientos esperados, pero que también implica la posibilidad de perder valor.

Ejemplo

Función de Utilidad de un individuo de riesgo (evitación de riesgos)

Función de Utilidad de un individuo neutra de riesgo

Función de Utilidad de un individuo amante del riesgo (verking)

CE – Cierta equivalente; E(U(W)) – Valor esperado de la utilidad (la utilidad prevista) del pago incierto W; E(W) – Valor esperado del pago incierto; U(CE) – Utilidad del equivalente de certeza; U(E(W)) – Utilidad del valor esperado del pago incierto; U(W)₀) – Utilidad del pago mínimo; U(W)₁) – Utilidad del pago máximo; W₀ – Pago mínimo; W₁ – Pago máximo; RP – prima de riesgo

A una persona se le da a elegir entre dos escenarios: uno con un pago garantizado y otro con un pago arriesgado con el mismo valor promedio. En el primer escenario, la persona recibe $50. En el escenario incierto, se lanza una moneda para decidir si la persona recibe $100 o nada. El pago esperado para ambos escenarios es de $50, lo que significa que a una persona que no sea sensible al riesgo no le importará si acepta el pago garantizado o la apuesta. Sin embargo, los individuos pueden tener diferentes actitudes de riesgo.

Se dice que una persona es:

• riesgo averso (o riesgo) - si aceptarían un determinado pago (el equivalente de certeza) de menos de $50 (por ejemplo, $40), en lugar de tomar la apuesta y posiblemente no recibir nada.
• riesgo neutral – si son indiferentes entre la apuesta y un cierto pago de $50.
• riesgo (o riesgo) – si aceptarían la apuesta incluso cuando el pago garantizado es más de $50 (por ejemplo, $60).

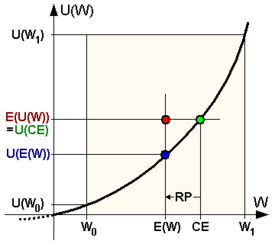
El pago promedio de la apuesta, conocido como valor esperado, es de $50. La cantidad de dólares más pequeña que un individuo estaría indiferente a gastar en una apuesta o garantía se denomina equivalente de certeza, que también se utiliza como medida de aversión al riesgo. Un individuo que tiene aversión al riesgo tiene un equivalente de certeza que es menor que la predicción de ganancias inciertas. La prima de riesgo es la diferencia entre el valor esperado y el equivalente de certeza. Para las personas con aversión al riesgo, la prima de riesgo es positiva, para las personas neutrales al riesgo es cero y para las personas que aman el riesgo, su prima de riesgo es negativa.

Utilidad del dinero

En la teoría de la utilidad esperada, un agente tiene una función de utilidad u(c) donde c representa el valor que podría recibir en dinero o bienes (en el ejemplo anterior c podría ser $0 o $40 o $100).

La función de utilidad u(c) se define solo hasta una transformación afín positiva; en otras palabras, se podría agregar una constante al valor de u (c) para todos los c, y/o u(c) podría multiplicarse por un factor constante positivo, sin afectar las conclusiones.

Un agente posee aversión al riesgo si y solo si la función de utilidad es cóncava. Por ejemplo, u(0) podría ser 0, u(100) podría ser 10, u(40) podría ser 5, y para comparar u(50) podría ser 6.

La utilidad esperada de la apuesta anterior (con un 50 % de posibilidades de recibir 100 y un 50 % de posibilidades de recibir 0) es

E()u)=()u()0)+u()100))/2{displaystyle E(u)=(u(0)+u(100)/2},

y si la persona tiene la función de utilidad con u(0)=0, u(40)=5, y u(100) = 10, entonces la utilidad esperada de la apuesta es igual a 5, que es igual a la utilidad conocida de la cantidad 40. Por lo tanto, el equivalente de certeza es 40.

La prima de riesgo es ($50 menos $40) = $10, o en términos proporcionales

()$ $ 50− − $ $ 40)/$ $ 40{displaystyle ($50-$40)/$40}

o 25% (donde $50 es el valor esperado de la apuesta arriesgada: (120+12100{displaystyle {tfrac}0+{tfrac {1}{2}100}). Esta prima de riesgo significa que la persona estaría dispuesta a sacrificar hasta $10 en valor esperado para lograr la certeza perfecta acerca de cuánto dinero será recibido. En otras palabras, la persona sería indiferente entre la apuesta y una garantía de $40, y preferiría cualquier cosa más de $ 40 a la apuesta.

En el caso de una persona más rica, el riesgo de perder $100 sería menos significativo y, para cantidades tan pequeñas, su función de utilidad probablemente sería casi lineal. Por ejemplo, si u(0) = 0 y u(100) = 10, entonces u(40) podría ser 4,02 y u(50) podría ser 5,01.

La función de utilidad para las ganancias percibidas tiene dos propiedades clave: una pendiente ascendente y concavidad. (i) La pendiente ascendente implica que la persona siente que más es mejor: una mayor cantidad recibida produce una mayor utilidad, y para apuestas arriesgadas la persona preferiría una apuesta estocásticamente dominante de primer orden sobre una apuesta alternativa (es decir, si la masa de probabilidad de la segunda apuesta se empuja hacia la derecha para formar la primera apuesta, luego se prefiere la primera apuesta). (ii) La concavidad de la función de utilidad implica que la persona tiene aversión al riesgo: siempre preferiría una cantidad segura a una apuesta arriesgada con el mismo valor esperado; además, para las apuestas arriesgadas, la persona preferiría una apuesta que sea una contracción que conserva la media de una apuesta alternativa (es decir, si parte de la masa de probabilidad de la primera apuesta se distribuye sin alterar la media para formar la segunda apuesta, entonces se prefiere la primera apuesta).

Medidas de aversión al riesgo según la teoría de la utilidad esperada

Hay varias medidas de la aversión al riesgo expresadas por la función de utilidad dada. Varias formas funcionales usadas a menudo para funciones de utilidad están representadas por estas medidas.

Aversión absoluta al riesgo

Cuanto mayor es la curvatura u()c){displaystyle u(c)}, cuanto mayor sea la aversión de riesgo. Sin embargo, ya que las funciones de utilidad no se definen de forma única (se definen sólo hasta transformaciones afines), se necesita una medida que se mantenga constante con respecto a estas transformaciones en lugar de simplemente el segundo derivado de u()c){displaystyle u(c)}. Una de esas medidas es la Medición de aversión de riesgo absoluto ()ARA), después de los economistas Kenneth Arrow y John W. Pratt, también conocido como el coeficiente de aversión de riesgo absoluto, definido como

A()c)=− − u.()c)u.()c){displaystyle A(c)=-{frac {u'(c)}{u'(c)}}

Donde u.()c){displaystyle u'(c)} y u.()c){displaystyle u'(c)} denota los derivados primero y segundo con respecto a c{displaystyle c} de u()c){displaystyle u(c)}. Por ejemplo, si u()c)=α α +β β ln()c),{displaystyle u(c)=alpha +beta ln(c),} Así que... u.()c)=β β /c{displaystyle u'(c)=beta /c} y u.()c)=− − β β /c2,{displaystyle u'(c)=-beta /c^{2} entonces A()c)=1/c.{displaystyle A(c)=1/c.} Note cómo A()c){displaystyle A(c)} no depende de α α {displaystyle alpha } y β β ,{displaystyle beta} tan afinadas transformaciones de u()c){displaystyle u(c)} No lo cambies.

Las siguientes expresiones se relacionan con este término:

• Utilidad exponencial de la forma u()c)=1− − e− − α α c{displaystyle u(c)=1-e^{-alpha c} es único en exhibir aversión de riesgo absoluto constante (CARA): A()c)=α α {displaystyle A(c)=alpha } es constante con respecto a c.
• La aversión de riesgo absoluto hiperbólico (HARA) es la clase más general de funciones de utilidad que se utilizan generalmente en la práctica (específicamente, CRRA (aversión constante de riesgo relativo, ver más abajo), CARA (aversión constante de riesgo absoluto), y utilidad cuadrática toda la exposición HARA y se utilizan a menudo debido a su viabilidad matemática). Una función de utilidad exhibe HARA si su aversión de riesgo absoluto es una función hiperbólica, es decir,

A()c)=− − u.()c)u.()c)=1ac+b{displaystyle A(c)=-{frac {u'(c)}{u'(c)}={frac {1}{ac+b}}

La solución a esta ecuación diferencial (omitiendo los términos constantes aditivos y multiplicativos, que no afectan el comportamiento implícito de la función de utilidad) es:

u()c)=()c− − cs)1− − R1− − R{displaystyle u(c)={frac {(c-c_{s}{1-R}{1-R}}}

Donde R=1/a{displaystyle R=1/a} y cs=− − b/a{displaystyle C_{s}=-b/a}. Note que cuando a=0{displaystyle a=0}, esto es CARA, como A()c)=1/b=const{displaystyle A(c)=1/b=const}, y cuando b=0{displaystyle b=0}, esto es CRRA (ver abajo), como cA()c)=1/a=const{displaystyle cA(c)=1/a=const}. See

• Reducción/aumento de la aversión del riesgo absoluto (DARA/IARA) está presente si A()c){displaystyle A(c)} está disminuyendo/aumentando. Utilizando la definición anterior de ARA, la siguiente desigualdad sostiene para DARA:

<math alttext="{displaystyle {frac {partial A(c)}{partial c}}=-{frac {u'(c)u'''(c)-[u''(c)]^{2}}{[u'(c)]^{2}}}∂ ∂ A()c)∂ ∂ c=− − u.()c)u′′()c)− − [u.()c)]2[u.()c)]2.0{displaystyle {frac {partial A(c)}{partial c}=-{frac {u'(c)u''''(c)-[u'''(c)}{2}{[u'(c)}} {}{2}}}} {0}}}} {c]<img alt="frac{partial A(c)}{partial c} = -frac{u'(c)u'''(c) - [u''(c)]^2}{[u'(c)]^2}

y esto sólo puede aguantar si 0}" xmlns="http://www.w3.org/1998/Math/MathML">u′′()c)■0{displaystyle u''(c)}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/201797d7118601acde858b6c6d07b75f0cef3caf" style="vertical-align: -0.838ex; width:9.996ex; height:3.009ex;"/>. Por lo tanto, DARA implica que la función de utilidad se asienta positivamente; es decir, 0}" xmlns="http://www.w3.org/1998/Math/MathML">u′′()c)■0{displaystyle u''(c)}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/201797d7118601acde858b6c6d07b75f0cef3caf" style="vertical-align: -0.838ex; width:9.996ex; height:3.009ex;"/>. Análogamente, la IARA puede derivarse de las direcciones opuestas de las desigualdades, lo que permite pero no requiere una función de utilidad negativa (<math alttext="{displaystyle u'''(c)u′′()c).0{displaystyle u''(c) made0}<img alt="u'''(c)). Un ejemplo de una función de utilidad DARA es u()c)=log⁡ ⁡ ()c){displaystyle u(c)=log(c)}, con A()c)=1/c{displaystyle A(c)=1/c}, mientras u()c)=c− − α α c2,{displaystyle u(c)=c-alpha c^{2} 0}" xmlns="http://www.w3.org/1998/Math/MathML">α α ■0{displaystyle alpha œ0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/edd4f784b6e8bb68fa774213ceacbab2d97825dc" style="vertical-align: -0.338ex; width:5.749ex; height:2.176ex;"/>, con A()c)=2α α /()1− − 2α α c){displaystyle A(c)=2alpha /(1-2alpha c)} representaría una función de utilidad cuadrática que exhibía IARA.

• La evidencia experimental y empírica es en su mayoría consistente con disminuir la aversión absoluta de riesgo.
• Contrariamente a lo que han asumido varios estudios empíricos, la riqueza no es un buen proxy para la aversión del riesgo al estudiar la distribución del riesgo en un entorno principal-agente. Aunque A()c)=− − u.()c)u.()c){displaystyle A(c)=-{frac {u'(c)}{u'(c)}} es monotónico en la riqueza bajo DARA o IARA y constante en la riqueza bajo CARA, pruebas de riesgo contractual que se basan en la riqueza como un proxy para la aversión absoluta de riesgo generalmente no se identifican.

Aversión al riesgo relativa

La medida Arrow-Pratt de aversión relativa al riesgo (RRA) o coeficiente de aversión relativa al riesgo se define como

R()c)=cA()c)=− − cu.()c)u.()c){displaystyle R(c)=cA(c)={frac {-cu'(c)}{u'(c)}}}.

A diferencia de ARA cuyas unidades están en $⁻¹, RRA es una cantidad sin dimensión, que permite que se aplique universalmente. Como para la aversión de riesgo absoluto, los términos correspondientes aversión constante de riesgo relativo (CRRA) and disminución/aumento de la aversión relativa del riesgo (DRRA/IRRA) se utilizan. Esta medida tiene la ventaja de que sigue siendo una medida válida de la aversión de riesgo, incluso si la función de utilidad cambia de riesgo averso a riesgo amor como c varies, es decir, la utilidad no es estrictamente convex/concave sobre todos c. Un RRA constante implica un ARA decreciente, pero el reverso no siempre es cierto. Como ejemplo específico de la aversión constante de riesgo relativo, la función de utilidad u()c)=log⁡ ⁡ ()c){displaystyle u(c)=log(c)} implica RRA = 1.

En los problemas de elección intertemporal, la elasticidad de sustitución intertemporal a menudo no se puede separar del coeficiente de aversión al riesgo relativo. La función de utilidad isoelástica

u()c)=c1− − *** *** − − 11− − *** *** {displaystyle u(c)={frac^{1-rho - Sí.

exhibe aversión constante de riesgo relativo con R()c)=*** *** {displaystyle R(c)=rho } y la elasticidad de la sustitución intertemporal ε ε u()c)=1/*** *** {displaystyle varepsilon _{u(c)}=1/rho }. Cuando *** *** =1,{displaystyle rho =1,} usando la regla de l'Hôpital muestra que esto simplifica el caso utilidad de registro, u()c) = registro c, y el efecto de los ingresos y la sustitución en el ahorro exactamente compensado.

Se puede considerar una aversión al riesgo relativa variable en el tiempo.

Implicaciones de aumentar/disminuir la aversión al riesgo absoluta y relativa

Las implicaciones más directas de aumentar o disminuir la aversión al riesgo absoluta o relativa, y las que motivan un enfoque en estos conceptos, ocurren en el contexto de formar una cartera con un activo riesgoso y un activo libre de riesgo. Si la persona experimenta un aumento en la riqueza, optará por aumentar (o mantener sin cambios, o disminuir) la cantidad de dólares del activo de riesgo mantenido en la cartera si es absoluto la aversión al riesgo es decreciente (o constante, o creciente). Por lo tanto, los economistas evitan utilizar funciones de utilidad como la cuadrática, que muestran una creciente aversión absoluta al riesgo, porque tienen una implicación conductual poco realista.

Del mismo modo, si la persona experimenta un aumento de la riqueza, optará por aumentar (o mantener sin cambios, o disminuir) la fracción de la cartera mantenida en el activo de riesgo si la aversión relativa al riesgo está disminuyendo (o constante, o aumentando).

En un modelo de economía monetaria, un aumento en la aversión relativa al riesgo aumenta el impacto de los hogares' tenencias de dinero en la economía en general. En otras palabras, cuanto más aumente la aversión relativa al riesgo, más shocks de demanda de dinero impactarán en la economía.

Teoría de la cartera

En la teoría de cartera moderna, la aversión al riesgo se mide como la recompensa adicional esperada que un inversor necesita para aceptar un riesgo adicional. Si un inversor tiene aversión al riesgo, invertirá en múltiples activos inciertos, pero solo cuando el rendimiento previsto de una cartera que es incierta sea mayor que el rendimiento previsto de una cartera que no es incierta, el inversor preferirá el primero. Aquí, el espectro riesgo-rendimiento es relevante, ya que resulta en gran medida de este tipo de aversión al riesgo. Aquí el riesgo se mide como la desviación estándar del rendimiento de la inversión, es decir, la raíz cuadrada de su varianza. En la teoría avanzada de carteras, se tienen en cuenta diferentes tipos de riesgo. Se miden como la n-ésima raíz del n-ésimo momento central. El símbolo utilizado para la aversión al riesgo es A o A_n.

A=dE()c)dσ σ {displaystyle A={frac {dE(c)}{dsigma }

An=dE()c)dμ μ nn{displaystyle A_{n}={frac {dE(c)}{d{sqrt[{n]{mu] ♪♪

Teorema de la utilidad de Von Neumann-Morgenstern

El teorema de utilidad de von Neumann-Morgenstern es otro modelo que se utiliza para indicar cómo la aversión al riesgo influye en la función de utilidad de un actor. Una extensión de la función de utilidad esperada, el modelo de von Neumann-Morgenstern incluye la aversión al riesgo de manera axiomática en lugar de como una variable adicional.

John von Neumann y Oskar Morgenstern desarrollaron por primera vez el modelo en su libro Teoría de juegos y comportamiento económico. Esencialmente, von Neumann y Morgenstern plantearon la hipótesis de que los individuos buscan maximizar su utilidad esperada en lugar de la ganancia monetaria esperada. valor de los activos. Al definir la utilidad esperada en este sentido, la pareja desarrolló una función basada en relaciones de preferencia. Como tal, si las preferencias de un individuo satisfacen cuatro axiomas clave, entonces se puede deducir una función de utilidad basada en cómo ponderan los diferentes resultados.

Al aplicar este modelo a la aversión al riesgo, la función se puede usar para mostrar cómo las preferencias de ganancias y pérdidas de un individuo influirán en su función de utilidad esperada. Por ejemplo, si a una persona con aversión al riesgo que tiene $20 000 ahorrados se le da la opción de apostar $100 000 con un 30 % de posibilidades de ganar, es posible que aún no apueste por temor a perder sus ahorros. Sin embargo, esto no tiene sentido utilizando el modelo tradicional de utilidad esperada;

EU()A)=0.3()$ $ 100,000)+0.7()$ $ 0){displaystyle EU(A)=0.3($100,000)+0.7($0)}

EU()A)=$ $ 30,000{displaystyle EU(A)=$30,000}

$20,000}" xmlns="http://www.w3.org/1998/Math/MathML">EU()A)■$ $ 20,000{displaystyle EU(A)$20,000}$20,000}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/cbac9ebd813022466d33270581551902b438aa5a" style="vertical-align: -0.838ex; width:18.218ex; height:2.843ex;"/>

El modelo von Neumann-Morgenstern puede explicar este escenario. Basado en las relaciones de preferencia, una utilidad específica u{displaystyle u} se puede asignar a ambos resultados. Ahora la función se convierte;

EU()A)=0.3u()$ $ 100,000)+0.7u()$ $ 0){displaystyle EU(A)=0.3u($100,000)+0.7u($0)}

Para una persona aversa de riesgo, u{displaystyle u}equivaldría a un valor que significa que el individuo preferiría mantener sus $20,000 en ahorros que apostarlo todo para aumentar potencialmente su riqueza a $ 100.000. Por lo tanto, una función de riesgo averso de los individuos demostraría que;

EU()A)≺ ≺ $ $ 20,000()keepingsavings){displaystyle EU(A)prec$20,000(keepingsavings)}

Limitaciones del tratamiento de utilidad esperada de la aversión al riesgo

Se ha criticado el uso del enfoque de la teoría de la utilidad esperada sobre la aversión al riesgo para analizar decisiones de apuestas pequeñas. Matthew Rabin ha demostrado que un individuo adverso al riesgo y maximizador de la utilidad esperada que,

de cualquier nivel de riqueza inicial [...] rechaza apuestas en las que pierde $100 o gana $110, cada una con un 50% de probabilidad [...] rechazará 50–50 apuestas de perder $1,000 o ganar cualquier suma de dinero.

Rabin critica esta implicación de la teoría de la utilidad esperada sobre la base de su inverosimilitud: las personas que tienen aversión al riesgo en apuestas pequeñas debido a la disminución de la utilidad marginal exhibirían formas extremas de aversión al riesgo en decisiones arriesgadas con apuestas más grandes. Una solución al problema observado por Rabin es la propuesta por la teoría de la perspectiva y la teoría de la perspectiva acumulativa, donde los resultados se consideran en relación con un punto de referencia (generalmente el statu quo), en lugar de considerar solo la riqueza final.

Otra limitación es el efecto reflejo, que demuestra la inversión de la aversión al riesgo. Este efecto fue presentado por primera vez por Kahneman y Tversky como parte de la teoría de la perspectiva, en el dominio de la economía del comportamiento. El efecto de reflexión es un patrón identificado de preferencias opuestas entre perspectivas negativas y positivas: las personas tienden a evitar el riesgo cuando la apuesta es entre ganancias y buscan riesgos cuando la apuesta es entre pérdidas. Por ejemplo, la mayoría de las personas prefieren una cierta ganancia de 3000 a una probabilidad del 80 % de una ganancia de 4000. Cuando se plantea el mismo problema, pero con pérdidas, la mayoría de la gente prefiere una probabilidad del 80% de una pérdida de 4.000 a una pérdida segura de 3.000.

El efecto de reflexión (así como el efecto de certeza) es inconsistente con la hipótesis de la utilidad esperada. Se supone que el principio psicológico que está detrás de este tipo de comportamiento es la sobrevaloración de la certeza. Las opciones que se perciben como seguras están sobre ponderadas en relación con las opciones inciertas. Este patrón es una indicación de un comportamiento de búsqueda de riesgo en perspectivas negativas y elimina otras explicaciones del efecto de certeza, como la aversión a la incertidumbre o la variabilidad.

Los hallazgos iniciales sobre el efecto de reflexión enfrentaron críticas en cuanto a su validez, ya que se afirmó que no hay evidencia suficiente para respaldar el efecto a nivel individual. Posteriormente, una extensa investigación reveló sus posibles limitaciones, lo que sugiere que el efecto es más frecuente cuando se trata de cantidades pequeñas o grandes y probabilidades extremas.

Negociación y aversión al riesgo

Numerosos estudios han demostrado que, en escenarios de negociación sin riesgo, tener aversión al riesgo es una desventaja. Además, el oponente siempre preferirá jugar contra la persona más adversa al riesgo. Basado tanto en el modelo de von Neumann-Morgenstern como en el de la teoría de juegos de Nash, una persona con aversión al riesgo recibirá felizmente una porción más pequeña de la oferta. Esto se debe a que su función de utilidad es cóncava, por lo que su utilidad aumenta a una tasa decreciente, mientras que sus oponentes que no tienen aversión al riesgo pueden aumentar a una tasa constante o creciente. Intuitivamente, una persona con aversión al riesgo se conformará con una parte menor del trato en comparación con una persona neutral al riesgo o que busca el riesgo.

En el cerebro

Las actitudes hacia el riesgo han atraído el interés del campo de la neuroeconomía y la economía del comportamiento. Un estudio de 2009 de Christopoulos et al. sugirió que la actividad de un área específica del cerebro (la circunvolución frontal inferior derecha) se correlaciona con la aversión al riesgo, y que los participantes con mayor aversión al riesgo (es decir, aquellos que tienen primas de riesgo más altas) también tienen respuestas más altas a opciones más seguras. Este resultado coincide con otros estudios, que muestran que la neuromodulación de la misma área hace que los participantes tomen decisiones más o menos adversas al riesgo, dependiendo de si la modulación aumenta o disminuye la actividad del área objetivo.

Comprensión pública y riesgo en actividades sociales

En el mundo real, muchas agencias gubernamentales, p. Ejecutivo de Salud y Seguridad, son fundamentalmente reacios al riesgo en su mandato. Esto muchas veces significa que exigen (con poder de aplicación legal) que se minimicen los riesgos, incluso a costa de perder la utilidad de la actividad riesgosa. Es importante considerar el costo de oportunidad al mitigar un riesgo; el costo de no tomar la acción riesgosa. Redactar leyes centradas en el riesgo sin el equilibrio de la utilidad puede tergiversar los objetivos de la sociedad. La comprensión pública del riesgo, que influye en las decisiones políticas, es un área que recientemente ha sido reconocida como merecedora de atención. En 2007, la Universidad de Cambridge inició la cátedra Winton de comprensión pública del riesgo, una función descrita como divulgación en lugar de investigación académica tradicional por el titular, David Spiegelhalter.

Niños

Los servicios para niños, como las escuelas y los parques infantiles, se han convertido en el foco de gran parte de la planificación con aversión al riesgo, lo que significa que a menudo se impide que los niños se beneficien de actividades que de otro modo habrían tenido. Muchos parques infantiles han sido equipados con superficies de alfombras que absorben los impactos. Sin embargo, estos solo están diseñados para salvar a los niños de la muerte en caso de caídas directas sobre sus cabezas y no logran sus objetivos principales. Son caros, lo que significa que hay menos recursos disponibles para beneficiar a los usuarios de otras maneras (como construir un parque infantil más cerca de la casa del niño, reduciendo el riesgo de un accidente de tráfico en el camino hacia él), y—algunos argumentar: los niños pueden intentar actos más peligrosos, con confianza en la superficie artificial. Shiela Sage, consejera escolar de primeros años, observa: "Los niños que solo se mantienen en lugares muy seguros no son los que pueden resolver los problemas por sí mismos. Los niños necesitan tener cierta capacidad para asumir riesgos... para que sepan cómo salir de las situaciones."

Programas de juegos e inversiones

Un estudio experimental con sujetos estudiantes que jugaban el juego del programa de televisión Deal or No Deal descubre que las personas tienen más aversión al riesgo en el centro de atención que en el anonimato de un laboratorio de comportamiento típico. En los tratamientos de laboratorio, los sujetos tomaron decisiones en un entorno de laboratorio computarizado estándar, como se emplea normalmente en los experimentos de comportamiento. En los tratamientos destacados, los sujetos hicieron sus elecciones en un entorno de programa de juegos simulado, que incluía una audiencia en vivo, un presentador de programas de juegos y cámaras de video. De acuerdo con esto, los estudios sobre el comportamiento de los inversores encuentran que los inversores comercian cada vez más especulativamente después de cambiar del comercio por teléfono al comercio en línea y que los inversores tienden a mantener sus inversiones principales con corredores tradicionales y usan una pequeña fracción de su riqueza para especular en línea.

El enfoque conductual de la situación laboral

La base de la teoría, sobre la conexión entre la situación laboral y la aversión al riesgo, es el nivel variable de ingresos de las personas. En promedio, las personas con ingresos más altos tienen menos aversión al riesgo que las personas con ingresos más bajos. En términos de empleo, cuanto mayor es la riqueza de un individuo, menos aversión al riesgo puede permitirse ser, y está más inclinado a pasar de un trabajo seguro a una empresa empresarial. La literatura asume que un pequeño aumento en los ingresos o la riqueza inicia la transición del empleo al emprendimiento basado en las preferencias de aversión absoluta al riesgo decreciente (DARA), aversión absoluta al riesgo constante (CARA) y aversión absoluta al riesgo creciente (IARA) como propiedades en su función de utilidad. La perspectiva de distribución del riesgo también se puede utilizar como un factor en la transición de la situación laboral, solo si la fuerza de la aversión al riesgo a la baja supera la fuerza de la aversión al riesgo. Si se utiliza el enfoque conductual para modelar la decisión de un individuo sobre su situación laboral, debe haber más variables además de la aversión al riesgo y cualquier preferencia absoluta por la aversión al riesgo.

Los efectos de los incentivos son un factor en el enfoque conductual que adopta una persona al decidir pasar de un trabajo seguro a la iniciativa empresarial. Los incentivos no financieros proporcionados por un empleador pueden cambiar la decisión de hacer la transición al espíritu empresarial, ya que los beneficios intangibles ayudan a fortalecer la aversión al riesgo de un individuo en relación con la fuerza de la aversión al riesgo a la baja. Las funciones de utilidad no equivalen a tales efectos y, a menudo, pueden arruinar el camino de comportamiento estimado que toma un individuo hacia su estado laboral.

El diseño de experimentos, para determinar a qué aumento de riqueza o ingresos cambiaría un individuo su situación laboral de un puesto de seguridad a empresas más riesgosas, debe incluir especificaciones de utilidad flexibles con incentivos sobresalientes integrados con preferencias de riesgo. La aplicación de experimentos relevantes puede evitar la generalización de diferentes preferencias individuales mediante el uso de este modelo y sus funciones de utilidad específicas.