Autómata de empuje hacia abajo

Clases de automata

(Haga clic en cada capa obtiene un artículo sobre ese tema)

En la teoría de la computación, una rama de la informática teórica, un autómata pushdown (PDA) es un tipo de autómata que emplea una pila.

Los autómatas pushdown se utilizan en teorías sobre lo que pueden calcular las máquinas. Son más capaces que las máquinas de estado finito pero menos capaces que las máquinas de Turing (ver más abajo). Los autómatas pushdown deterministas pueden reconocer todos los lenguajes libres de contexto deterministas, mientras que los no deterministas pueden reconocer todos los lenguajes libres de contexto, y el primero se usa a menudo en el diseño del analizador.

El término "pushdown" se refiere al hecho de que la pila puede considerarse como "empujada hacia abajo" como un dispensador de bandejas en una cafetería, ya que las operaciones nunca funcionan en elementos que no sean el elemento superior. Un autómata de pila, por el contrario, permite el acceso y las operaciones en elementos más profundos. Los autómatas de pila pueden reconocer un conjunto estrictamente mayor de idiomas que los autómatas de inserción. Un autómata de pila anidada permite el acceso completo y también permite que los valores apilados sean subpilas completas en lugar de solo símbolos finitos únicos.

Descripción informal

Un diagrama de un autómata empuje

Una máquina de estado finito solo mira la señal de entrada y el estado actual: no tiene una pila con la que trabajar. Elige un nuevo estado, el resultado de seguir la transición. Un autómata pushdown (PDA) se diferencia de una máquina de estados finitos en dos aspectos:

1. Puede utilizar la parte superior de la pila para decidir qué transición tomar.
2. Puede manipular la pila como parte de realizar una transición.

Un autómata pushdown lee una cadena de entrada determinada de izquierda a derecha. En cada paso, elige una transición indexando una tabla por símbolo de entrada, estado actual y el símbolo en la parte superior de la pila. Un autómata pushdown también puede manipular la pila, como parte de la realización de una transición. La manipulación puede ser empujar un símbolo en particular a la parte superior de la pila o sacarlo de la parte superior de la pila. El autómata puede alternativamente ignorar la pila y dejarla como está.

Combinar: dado un símbolo de entrada, un estado actual y un símbolo de pila, el autómata puede seguir una transición a otro estado y, opcionalmente, manipular (empujar o sacar) la pila.

Si, en cada situación, como máximo una de estas acciones de transición es posible, entonces el autómata se denomina autómata de empuje determinista (DPDA). En general, si varias acciones son posibles, entonces el autómata se denomina general, o no determinista, PDA. Una cadena de entrada dada puede conducir un autómata pushdown no determinista a una de varias secuencias de configuración; si uno de ellos conduce a una configuración de aceptación después de leer la cadena de entrada completa, se dice que este último pertenece al lenguaje aceptado por el autómata.

Definición formal

Usamos notación formal estándar del lenguaje: ${displaystyle Gamma ^{*}$ denota el conjunto de cuerdas de longitud finita sobre el alfabeto ${displaystyle "Gamma"$ y ${displaystyle varepsilon }$ denota la cuerda vacía.

Una PDA se define formalmente como una tupla de 7:

${displaystyle M=(Q,SigmaGammadeltaq_{0},Z,F)}$Donde

• ${displaystyle Q}$ es un conjunto finito de estados
• ${displaystyle Sigma }$ es un conjunto finito que se llama entrada
• ${displaystyle "Gamma"$ es un conjunto finito que se llama pila alfabeto
• ${displaystyle delta }$ es un subconjunto finito de ${displaystyle Qtimes (Sigma cup {varepsilon })times Gamma times Qtimes Gamma ^{*}$, el relación de transición
• ${displaystyle q_{0}in Q}$ es start state
• ${displaystyle Zin Gamma }$ es pila inicial símbolo
• ${displaystyle Fsubseteq Q}$ es el conjunto de aceptar estados

Un elemento ${displaystyle (p,a,A,q,alpha)in delta }$ es una transición ${displaystyle M}$. Tiene el significado previsto de que ${displaystyle M}$, en estado ${displaystyle pin Q}$, en la entrada ${displaystyle ain Sigma cup {varepsilon}}$ y con ${displaystyle Ain Gamma }$ como símbolo de pila más alto, puede leer ${displaystyle a}$, cambiar el estado a ${displaystyle q}$, pop ${displaystyle A}$, reemplazándolo empujando ${displaystyle alpha in Gamma ^{*}$. El ${displaystyle (Sigma cup {varepsilon })}$ componente de la relación de transición se utiliza para formalizar que el PDA puede leer una carta de la entrada, o proceder dejando la entrada intacta.

En muchos textos, la relación de transición se reemplaza por una formalización (equivalente), donde

• ${displaystyle delta }$ es función de transición, cartografía ${displaystyle Qtimes (Sigma cup {varepsilon })times Gamma }$ en subconjuntos finitos ${displaystyle Qtimes Gamma ^{*}$

Aquí. ${displaystyle delta (p,a,A)}$ contiene todas las acciones posibles en el estado ${displaystyle p}$ con ${displaystyle A}$ en la pila, mientras la lectura ${displaystyle a}$ en la entrada. Uno escribe por ejemplo ${displaystyle delta (p,a,A)={(q,BA)}}$ precisamente cuando ${displaystyle (q,BA)in {(q,BA)},(q,BA)in delta (p,a,A),}$ porque ${displaystyle ((p,a,A),{(q,BA)})in delta }$. Note que finito en esta definición es esencial.

Cálculos

un paso del automatón de empuje

Con el fin de formalizar la semántica del automaton pushdown se introduce una descripción de la situación actual. Cualquier 3-tuple ${displaystyle (p,w,beta)en Qtimes Sigma ^{*}times Gamma ^{*}$ se llama una descripción instantánea (ID) de ${displaystyle M}$, que incluye el estado actual, la parte de la cinta de entrada que no se ha leído, y el contenido de la pila (el símbolo más alto escrito primero). La relación de transición ${displaystyle delta }$ define la relación paso-paso ${displaystyle vdash _{M}$ de ${displaystyle M}$ en descripciones instantáneas. Para instrucción ${displaystyle (p,a,A,q,alpha)in delta }$ existe un paso ${displaystyle (p,ax,Agamma)vdash _{M}(q,x,alpha gamma)}$, por cada ${displaystyle xin Sigma ^{*}$ y todos ${displaystyle gamma in Gamma ^{*}$.

En general, las automatas de empuje son significado no determinante que en una descripción instantánea dada ${displaystyle (p,w,beta)}$ puede haber varios pasos posibles. Cualquiera de estos pasos puede ser elegido en un cálculo. Con la definición anterior en cada paso siempre aparece un solo símbolo (top de la pila), sustituyendolo con tantos símbolos como sea necesario. Como consecuencia, ningún paso se define cuando la pila está vacía.

Las computaciones del automaton de empuje son secuencias de pasos. El cálculo comienza en el estado inicial ${displaystyle q_{0}$ con el símbolo de pila inicial ${displaystyle Z}$ en la pila, y una cuerda ${displaystyle w}$ en la cinta de entrada, con la descripción inicial ${displaystyle (q_{0},w,Z)}$. Hay dos modos de aceptar. El autómata pushdown acepta por estado final, lo que significa después de leer su entrada el autómata llega a un estado aceptado (en ${displaystyle F}$), o acepta por pila vacía (${displaystyle varepsilon }$), lo que significa después de leer su entrada el autómata vacía su pila. El primer modo de aceptación utiliza la memoria interna (estado), el segundo la memoria externa (estado).

Formalmente uno define

1. ${displaystyle L(M)={win Sigma ^{*} impertine(q_{0},w,Z)vdash ¿Qué?$ con ${displaystyle fin F}$ y ${displaystyle gamma in Gamma ^{*}}$ (Estado final)
2. ${displaystyle N(M)={win Sigma ^{*} impertine(q_{0},w,Z)vdash ¿Qué?$ con ${displaystyle qin Q}}$ (pila vacía)

Aquí. ${displaystyle vdash _{*}}$ representa el cierre reflexivo y transitivo de la relación paso ${displaystyle vdash _{M}$ significando cualquier número de pasos consecutivos (cero, uno o más).

Para cada autómata pushdown, estos dos lenguajes no necesitan tener ninguna relación: pueden ser iguales, pero por lo general este no es el caso. Una especificación del autómata también debe incluir el modo previsto de aceptación. Tomando el control de todos los autómatas pushdown, ambas condiciones de aceptación definen la misma familia de lenguajes.

Teorema. Para cada automatón de empuje ${displaystyle M}$ uno puede construir un autómata empuje ${displaystyle M'}$ tales que ${displaystyle L(M)=N(M)}$, y viceversa, para cada automatón empuje ${displaystyle M}$ uno puede construir un autómata empuje ${displaystyle M'}$ tales que ${displaystyle N(M)=L(M)}$

Ejemplo

A continuación figura la descripción formal del PDA que reconoce el idioma ${displaystyle {0^{n}1}mid ngq.$ por estado final:

PDA ${displaystyle {0^{n}1}mid ngq.$
(por estado final)

${displaystyle M=(Q, Sigma Gamma delta q_{0}, Z, F)}$, donde

• estados: ${displaystyle Q={p,q,r}$
• alfabeto de entrada: ${displaystyle Sigma ={0,1}}$
• pila alfabeto: ${displaystyle "Gamma"$
• start state: ${displaystyle q_{0}=p}$
• símbolo de arranque: Z
• aceptar estados: ${displaystyle F={r}$

La relación de transición ${displaystyle delta }$ consta de las siguientes seis instrucciones:

${displaystyle (p,0,Z,p,AZ)}$,

${displaystyle (p,0,A,p,AA)}$,

${displaystyle (p,epsilonZ,q,Z)}$,

${displaystyle (p,epsilonA,q,A)}$,

${displaystyle (q,1,A,q,epsilon)}$, y

${displaystyle (q,epsilonZ,r,Z)}$.

En palabras, las dos primeras instrucciones dicen que en el estado p en cualquier momento el símbolo Se lee 0, una A es empujado hacia la pila. Empujar el símbolo A encima de otro A se formaliza reemplazando la parte superior A por AA (y de manera similar para insertar el símbolo A encima de un Z).

Las instrucciones tercera y cuarta dicen que, en cualquier momento, el autómata puede pasar del estado p al estado q.

La quinta instrucción dice que en el estado q, para cada símbolo 1 leído, aparece una A.

Finalmente, la sexta instrucción dice que la máquina puede pasar del estado q al estado de aceptación r solo cuando la pila consta de una sola Z.

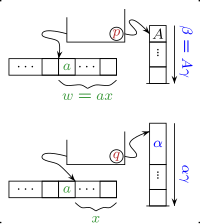
Parece que no hay representación generalmente utilizada para la PDA. Aquí hemos representado la instrucción ${displaystyle (p,a,A,q,alpha)}$ por un borde del estado p al estado q etiquetado por ${displaystyle a;A/alpha }$ (Leer a; sustitúyase A por ${displaystyle alpha }$).

Comprender el proceso de cálculo

aceptar computación para 0011

Lo siguiente ilustra cómo el PDA anterior compute en diferentes cadenas de entrada. El subscript M desde el símbolo paso ${displaystyle vdash }$ está aquí omitido.

PDA y lenguajes libres de contexto

Cada gramática independiente del contexto se puede transformar en un autómata pushdown no determinista equivalente. El proceso de derivación de la gramática se simula por la izquierda. Donde la gramática reescribe un no terminal, el PDA toma el no terminal superior de su pila y lo reemplaza por la parte derecha de una regla gramatical (expand). Cuando la gramática genera un símbolo de terminal, la PDA lee un símbolo de la entrada cuando es el símbolo superior de la pila (coincidencia). En cierto sentido, la pila de la PDA contiene los datos no procesados de la gramática, correspondientes a un recorrido preordenado de un árbol de derivación.

Técnicamente, dada una gramática libre de contexto, el PDA tiene un solo estado, 1, y su relación de transición se construye de la siguiente manera.

1. ${displaystyle (1,varepsilonA,1,alpha)}$ para cada regla ${displaystyle Ato alpha }$ ()Ampliación)
2. ${displaystyle (1,a,a,1,varepsilon)}$ para cada símbolo terminal ${displaystyle a}$ ()partido)

La PDA acepta por pila vacía. Su símbolo de pila inicial es el símbolo de inicio de la gramática.

Para una gramática libre de contexto en la forma normal de Greibach, definiendo (1,γ) ∈ δ(1,a,A) para cada regla gramatical A → aγ también produce un autómata pushdown no determinista equivalente.

Lo contrario, encontrar una gramática para un PDA dado, no es tan fácil. El truco consiste en codificar dos estados de la PDA en los no terminales de la gramática.

Teorema. Para cada automatón de empuje ${displaystyle M}$ uno puede construir una gramática sin contexto ${displaystyle G.$ tales que ${displaystyle N(M)=L(G)}$.

El lenguaje de las cadenas aceptadas por un automaton de empuje determinista (DPDA) se llama un lenguaje determinista sin contexto. No todos los idiomas sin contexto son deterministas. En consecuencia, el DPDA es una variante estrictamente más débil del PDA. Incluso para los idiomas regulares, hay un problema de explosión de tamaño: para cualquier función recursiva ${displaystyle f}$ y para enteros arbitrariamente grandes ${displaystyle n}$, hay un PDA de tamaño ${displaystyle n}$ describiendo un idioma regular cuyo DPDA más pequeño tiene al menos ${displaystyle f(n)}$ estados. Para muchos PDA no ordinarios, cualquier DPDA equivalente requeriría un número ilimitado de estados.

Un autómata finito con acceso a dos pilas es un dispositivo más potente, equivalente en potencia a una máquina de Turing. Un autómata lineal acotado es un dispositivo que es más poderoso que un autómata de empuje hacia abajo pero menos que una máquina de Turing.

PDA y máquinas de Turing

Un autómata pushdown es computacionalmente equivalente a un 'restringido' Turing Machine (TM) con dos cintas que está restringida de la siguiente manera: en la primera cinta, la TM solo puede leer la entrada y moverse de izquierda a derecha (no puede realizar cambios). En la segunda cinta, solo puede 'empujar' y 'pop' datos. O de manera equivalente, puede leer, escribir y moverse hacia la izquierda y hacia la derecha con la restricción de que la única acción que puede realizar en cada paso es eliminar el carácter más a la izquierda en la cadena (pop) o agregar un carácter adicional a la izquierda. -la mayoría de los caracteres en la cadena (push).

Que una PDA sea más débil que una TM puede deberse al hecho de que el procedimiento 'pop' borra algunos datos. Para hacer que una PDA sea tan fuerte como una TM, necesitamos guardar en algún lugar los datos perdidos a través de 'pop'. Podemos lograr esto introduciendo una segunda pila. En el modelo TM de PDA del último párrafo, esto es equivalente a un TM con 3 cintas, donde la primera cinta es la cinta de entrada de solo lectura, y la segunda y la tercera cinta son 'push and pop'; (apilar) cintas. Para que una PDA de este tipo simule cualquier TM dado, damos la entrada de la PDA a la primera cinta, mientras mantenemos ambas pilas vacías. Luego pasa a enviar toda la entrada de la cinta de entrada a la primera pila. Cuando toda la entrada se transfiere a la primera pila, ahora procedemos como una MT normal, donde moverse hacia la derecha en la cinta es lo mismo que sacar un símbolo de la primera pila y empujar un símbolo (posiblemente actualizado) a la segunda pila, y moverse hacia la izquierda corresponde a sacar un símbolo de la segunda pila y empujar (un símbolo posiblemente actualizado) a la primera pila. Así tenemos una PDA con 2 pilas que puede simular cualquier TM.

Autómata de empuje generalizado (GPDA)

Un GPDA es un PDA que escribe una cadena completa de cierta longitud conocida en la pila o elimina una cadena completa de la pila en un solo paso.

Una GPDA se define formalmente como una tupla de 6:

${displaystyle M=(Q, Sigma Gamma delta q_{0}, F)}$

Donde ${displaystyle Q,Sigma ,Gamma ,q_{0}$, y ${displaystyle F}$ se definen de la misma manera que un PDA.

${displaystyle ,delta }$: ${displaystyle Qtimes Sigma _{epsilon }times Gamma ^{*}longrightarrow P(Qtimes Gamma ^{*}$

es la función de transición.

Las normas de computación de un GPDA son las mismas que un PDA excepto que las ${displaystyle a_{i+1}}$'s y ${displaystyle B_{i+1}$Ahora son cuerdas en lugar de símbolos.

GPDA's y PDA's son equivalentes en el sentido de que si un idioma es reconocido por un PDA, también lo es por un GPDA y viceversa.

Se puede formular una prueba analítica para la equivalencia de GPDA's y PDA's usando la siguiente simulación:

Vamos ${displaystyle delta (q_{1},w,x_{1}x_{2}cdot x_{m})longrightarrow (q_{2},y_{2}...y_{n}) }$ ser una transición del GPDA

Donde ${displaystyle q_{1},q_{2}in Q,win Sigma _{epsilon },x_{1},x_{2},ldotsx_{m}in Gamma ^{*},mgeq Oh, Dios mío. Gamma ^{*},ngeq 0}$.

Construya las siguientes transiciones para el PDA:

$################################################################################################################################################################################################################################################################$

Autómata de pila

Como una generalización de los autómatas pushdown, Ginsburg, Greibach y Harrison (1967) investigaron los autómatas apilados, que además pueden avanzar hacia la izquierda o hacia la derecha en la cadena de entrada (rodeados de símbolos finales especiales para evitar el deslizamiento). out) y subir o bajar en la pila en modo de solo lectura. Un autómata de pila se llama no borrado si nunca sale de la pila. La clase de lenguajes aceptados por los autómatas de pila no deterministas y que no borran es NSPACE(n²), que es un superconjunto de los lenguajes sensibles al contexto. La clase de lenguajes aceptados por los autómatas de pila deterministas que no se borran es DSPACE(n⋅log(n)).

Autómatas pushdown alternos

Un autómata de empuje alterno (APDA) es un autómata de empuje con un conjunto de estados

• ${displaystyle Q=Q_{exists }cup Q_{forall }$ Donde ${displaystyle Q_{exists }cap Q_{forall }=emptyset }$.

Estados Unidos ${displaystyle Q_{exists }$ y ${displaystyle Q_{forall}$ se llaman existencial Resp. universal. En un estado existencial un APDA elige sin determinación el siguiente estado y acepta si al menos uno de los cálculos resultantes acepta. En un estado universal APDA se mueve a todos los próximos estados y acepta si Todos los cálculos resultantes aceptan.

El modelo fue presentado por Chandra, Kozen y Stockmeyer. Ladner, Lipton y Stockmeyer demostraron que este modelo es equivalente a EXPTIME, es decir, un lenguaje es aceptado por alguna APDA si, y solo si, puede decidirse mediante un algoritmo de tiempo exponencial.

Aizikowitz y Kaminski introdujeron autómatas de empuje alternativos sincronizados (SAPDA) que son equivalentes a las gramáticas conjuntivas de la misma manera que los PDA no deterministas son equivalentes a las gramáticas libres de contexto.