Autómata celular de puntos cuánticos

Los autómatas celulares de puntos cuánticos (QDCA, a veces denominados simplemente autómatas celulares cuánticos o QCA) son una mejora propuesta en el diseño de computadoras convencionales (CMOS), que se han ideado en analogía con los modelos convencionales de autómatas celulares introducidos por John von Neumann.

Cualquier dispositivo diseñado para representar datos y realizar cálculos, independientemente de los principios físicos que utilice y de los materiales utilizados para construirlo, debe tener dos propiedades fundamentales: distinguibilidad y cambio de estado condicional, siendo que esta última implica la primera. Esto significa que dicho dispositivo debe tener barreras que permitan distinguir entre estados, y que debe tener la capacidad de controlar estas barreras para realizar cambios de estado condicionales. Por ejemplo, en un sistema electrónico digital, los transistores desempeñan el papel de tales barreras de energía controlables, lo que hace que sea extremadamente práctico realizar cálculos con ellos.

Un autómata celular (CA) es un sistema dinámico discreto que consiste en una cuadrícula uniforme (finita o infinita) de las células. Cada celda puede estar en solo uno de un número finito de estados en un momento discreto. A medida que avanza el tiempo, el estado de cada célula en la cuadrícula está determinado por una regla de transformación que factores en su estado anterior y los estados de las células inmediatamente adyacentes (la celda ' S " vecindario "). El ejemplo más conocido de un autómata celular es John Horton Conway ' S " Game of Life ", que describió en 1970.

Los autómatas celulares se implementan comúnmente como programas de software. Sin embargo, en 1993, Lent et al. propusieron una implementación física de un autómata utilizando células de puntos cuánticos. El autómata ganó popularidad rápidamente y se fabricó por primera vez en 1997. Lent combinó la naturaleza discreta de los autómatas celulares y la mecánica cuántica para crear dispositivos a escala nanométrica capaces de realizar cálculos a velocidades de conmutación muy altas (del orden de los terahercios) y consumir cantidades extremadamente pequeñas de energía eléctrica.

En la actualidad, el diseño estándar de celdas QCA de estado sólido considera que la distancia entre puntos cuánticos es de aproximadamente 20 nm y la distancia entre celdas de aproximadamente 60 nm. Al igual que cualquier CA, los autómatas celulares cuánticos (-punto) se basan en reglas de interacción simples entre celdas colocadas en una cuadrícula. Una celda QCA se construye a partir de cuatro puntos cuánticos dispuestos en un patrón cuadrado. Estos puntos cuánticos son sitios que los electrones pueden ocupar al hacer un túnel hacia ellos.

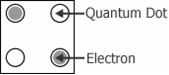
La figura 2 muestra un diagrama simplificado de una celda de puntos cuánticos. Si la celda está cargada con dos electrones, cada uno libre de hacer un túnel hacia cualquier sitio de la celda, estos electrones intentarán ocupar el sitio más alejado posible entre sí debido a la repulsión electrostática mutua. Por lo tanto, existen dos estados celulares distinguibles. La figura 3 muestra los dos posibles estados de energía mínima de una celda de puntos cuánticos. El estado de una celda se denomina polarización, denotada como P. Aunque se elige arbitrariamente, usar la polarización celular P = -1 para representar el “0” lógico y P = +1 para representar el “1” lógico se ha convertido en una práctica estándar.

Las disposiciones en cuadrícula de las celdas de puntos cuánticos se comportan de maneras que permiten el cálculo. La disposición práctica más simple de las celdas se logra colocando las celdas de puntos cuánticos en serie, una al lado de la otra. La Figura 4 muestra una disposición de este tipo de cuatro celdas de puntos cuánticos. Los cuadros delimitadores en la figura no representan la implementación física, sino que se muestran como un medio para identificar celdas individuales.

Si se cambiara la polarización de cualquiera de las celdas en la disposición que se muestra en la figura 4 (mediante una "celda controladora"), el resto de las celdas se sincronizarían inmediatamente con la nueva polarización debido a las interacciones coulombianas entre ellas. De esta manera, se puede crear un "cable" de celdas de puntos cuánticos que transmite el estado de polarización. Las configuraciones de dichos cables pueden formar un conjunto completo de puertas lógicas para la computación.

Existen dos tipos de cables posibles en QCA: un cable binario simple como se muestra en la Figura 4 y una cadena inversora, que se constituye colocando celdas QCA invertidas a 45 grados una al lado de la otra.

La compuerta mayoritaria y la compuerta inversora (NOT) se consideran los dos bloques de construcción más fundamentales de QCA. La Figura 5 muestra una compuerta mayoritaria con tres entradas y una salida. En esta estructura, el efecto del campo eléctrico de cada entrada sobre la salida es idéntico y aditivo, con el resultado de que cualquier estado de entrada ("binario 0" o "binario 1") que esté en la mayoría se convierte en el estado de la celda de salida, de ahí el nombre de la compuerta. Por ejemplo, si las entradas A y B existen en un estado de “binario 0” y la entrada C existe en un estado de “binario 1”, la salida existirá en un estado de “binario 0” ya que el efecto del campo eléctrico combinado de las entradas A y B juntas es mayor que el de la entrada C sola.

Se pueden construir otros tipos de puertas, a saber, puertas AND y puertas OR, utilizando una puerta mayoritaria con polarización fija en una de sus entradas. Una puerta NOT, por otro lado, es fundamentalmente diferente de la puerta mayoritaria, como se muestra en la Figura 6. La clave de este diseño es que la entrada se divide y ambas entradas resultantes inciden oblicuamente en la salida. A diferencia de una colocación ortogonal, el efecto del campo eléctrico de esta estructura de entrada fuerza una inversión de la polarización en la salida.

Existe una conexión entre las células de puntos cuánticos y los autómatas celulares. Las células solo pueden estar en uno de dos estados y el cambio condicional de estado en una célula está determinado por el estado de sus vecinos adyacentes. Sin embargo, es necesario un método para controlar el flujo de datos para definir la dirección en la que se produce la transición de estado en las células QCA. Los relojes de un sistema QCA sirven para dos propósitos: alimentar al autómata y controlar la dirección del flujo de datos. Los relojes QCA son áreas de material conductor debajo de la red del autómata, que modulan las barreras de tunelización de electrones en las células QCA que se encuentran sobre él.

Un reloj QCA induce cuatro etapas en las barreras de tunelización de las células que se encuentran por encima de él. En la primera etapa, las barreras de tunelización comienzan a elevarse. La segunda etapa se alcanza cuando las barreras de tunelización son lo suficientemente altas como para evitar que los electrones realicen el proceso. La tercera etapa ocurre cuando la barrera alta comienza a bajar. Y finalmente, en la cuarta etapa, las barreras de tunelización permiten que los electrones realicen el proceso nuevamente libremente. En palabras simples, cuando la señal del reloj es alta, los electrones tienen libertad para realizar el proceso. Cuando la señal del reloj es baja, la célula se bloquea.

La Figura 7 muestra una señal de reloj con sus cuatro etapas y los efectos en una celda en cada etapa de reloj. Un diseño QCA típico requiere cuatro relojes, cada uno de los cuales está desfasado cíclicamente 90 grados con respecto al reloj anterior. Si un cable horizontal constara, por ejemplo, de 8 celdas y cada par consecutivo, comenzando desde la izquierda, se conectara a cada reloj consecutivo, los datos fluirían naturalmente de izquierda a derecha. El primer par de celdas permanecerá bloqueado hasta que el segundo par de celdas se bloquee y así sucesivamente. De esta manera, la dirección del flujo de datos se puede controlar a través de las zonas de reloj.

El cruce de cables en las celdas QCA se puede realizar utilizando dos orientaciones de puntos cuánticos diferentes (una a 45 grados de la otra) y permitiendo que un cable compuesto de un tipo pase perpendicularmente "a través" de un cable del otro tipo, como se muestra esquemáticamente en la figura 8. Las distancias entre los puntos en ambos tipos de celdas son exactamente las mismas, lo que produce las mismas interacciones coulombianas entre los electrones de cada celda. Sin embargo, los cables compuestos de estos dos tipos de celdas son diferentes: un tipo propaga la polarización sin cambios; el otro invierte la polarización de una celda adyacente a la siguiente. La interacción entre los diferentes tipos de cables en el punto de cruce no produce ningún cambio neto de polarización en ninguno de los cables, lo que permite preservar las señales en ambos cables.

Aunque esta técnica es bastante simple, representa un enorme problema de fabricación. Un nuevo tipo de patrón de celdas potencialmente introduce hasta el doble de costos de fabricación e infraestructura; la cantidad de posibles ubicaciones de puntos cuánticos en una red intersticial se duplica y es inevitable un aumento general en la complejidad del diseño geométrico. Otro problema que presenta esta técnica es que el espacio adicional entre celdas de la misma orientación disminuye las barreras de energía entre el estado fundamental de una celda y su primer estado excitado. Esto degrada el rendimiento del dispositivo en términos de temperatura operativa máxima, resistencia a la entropía y velocidad de conmutación.

Christopher Graunke, David Wheeler, Douglas Tougaw y Jeffrey D. Will presentaron una técnica de cruce de cables diferente que hace que la fabricación de dispositivos QCA sea más práctica en su artículo “Implementación de una red de barras cruzadas utilizando autómatas celulares de puntos cuánticos”. El artículo no solo presenta un nuevo método de implementación de cruces de cables, sino que también brinda una nueva perspectiva sobre la sincronización de QCA.

Su técnica de cruce de cables introduce el concepto de implementar dispositivos QCA capaces de realizar cálculos en función de la sincronización. Esto implica la capacidad de modificar la función del dispositivo a través del sistema de relojería sin realizar ningún cambio físico en el dispositivo. Por lo tanto, el problema de fabricación mencionado anteriormente se aborda completamente mediante: a) el uso de un solo tipo de patrón de puntos cuánticos y, b) la capacidad de crear un bloque de construcción QCA universal de complejidad adecuada, cuya función está determinada únicamente por su mecanismo de temporización (es decir, sus relojes).

Sin embargo, la conmutación cuasi-adiabática requiere que las barreras de tunelización de una célula se conmuten de forma relativamente lenta en comparación con la velocidad de conmutación intrínseca de un QCA. Esto evita los estados de oscilación y metaestables que se observan cuando las células se conmutan de forma abrupta. Por lo tanto, la velocidad de conmutación de un QCA está limitada no por el tiempo que tarda una célula en cambiar de polarización, sino por el tiempo de conmutación cuasi-adiabático adecuado de los relojes que se utilizan.

Al diseñar un dispositivo capaz de realizar cálculos, a menudo es necesario convertir líneas de datos paralelas en un flujo de datos en serie. Esta conversión permite reducir diferentes fragmentos de datos a una serie de valores dependientes del tiempo en un solo cable. La Figura 9 muestra un dispositivo QCA de conversión de paralelo a serie de este tipo. Los números en las áreas sombreadas representan diferentes zonas de sincronización en fases consecutivas de 90 grados. Observe cómo todas las entradas están en la misma zona de sincronización. Si se controlaran los datos en paralelo en las entradas A, B, C y D, y luego no se controlaran más durante al menos las 15 fases de transmisión en serie restantes, la salida X presentaría los valores de D, C, B y A, en ese orden, en las fases tres, siete, once y quince. Si se añadiera una nueva región de sincronización en la salida, se podría sincronizar para bloquear un valor correspondiente a cualquiera de las entradas seleccionando correctamente un período de bloqueo de estado adecuado.

La nueva región de reloj de enclavamiento sería completamente independiente de las otras cuatro zonas de reloj ilustradas en la figura 9. Por ejemplo, si el valor de interés para la nueva región de enclavamiento fuera el valor que D presenta cada 16.ª fase, el mecanismo de reloj de la nueva región tendría que estar configurado para enclavar un valor en la 4.ª fase y cada 16.ª fase a partir de entonces, ignorando así todas las entradas excepto D.

Añadir una segunda línea serial al dispositivo y añadir otra región de enclavamiento permitiría el enclavamiento de dos valores de entrada en las dos salidas diferentes. Para realizar el cálculo, se añade una compuerta que toma como entradas ambas líneas seriales en sus respectivas salidas. La compuerta se coloca sobre una nueva región de enclavamiento configurada para procesar datos solo cuando ambas regiones de enclavamiento al final de las líneas seriales contienen los valores de interés en el mismo instante. La Figura 10 muestra una disposición de este tipo. Si se configuran correctamente, las regiones de enclavamiento 5 y 6 contendrán cada una valores de entrada de interés para la región de enclavamiento 7. En este instante, la región de enclavamiento 7 dejará pasar los valores enclavados en las regiones 5 y 6 a través de la compuerta AND, por lo que la salida podría configurarse para ser el resultado AND de dos entradas cualesquiera (es decir, R y Q) simplemente configurando las regiones de enclavamiento 5, 6 y 7.

Esto representa la flexibilidad para implementar 16 funciones, sin modificar el diseño físico. Obviamente, las líneas seriales adicionales y las entradas paralelas aumentarían el número de funciones realizables. Sin embargo, un inconveniente significativo de estos dispositivos es que, a medida que aumenta el número de funciones realizables, se requiere un número cada vez mayor de regiones de sincronización. Como consecuencia, un dispositivo que aproveche este método de implementación de funciones puede funcionar significativamente más lento que su contraparte tradicional.

En términos generales, existen cuatro clases diferentes de implementaciones de QCA: isla de metal, semiconductor, molecular y magnética.

La implementación de islas de metal fue la primera tecnología de fabricación creada para demostrar el concepto de QCA. Originalmente no se pensó para competir con la tecnología actual en cuanto a velocidad y practicidad, ya que sus propiedades estructurales no son adecuadas para diseños escalables. El método consiste en construir puntos cuánticos utilizando islas de aluminio. Los experimentos anteriores se implementaron con islas de metal de hasta 1 micrómetro de dimensión. Debido a que las islas son de tamaño relativamente grande, los dispositivos con islas de metal tuvieron que mantenerse a temperaturas extremadamente bajas para que los efectos cuánticos (cambio de electrones) fueran observables.

Las implementaciones de QCA de semiconductores (o de estado sólido) podrían utilizarse potencialmente para implementar dispositivos QCA con los mismos procesos de fabricación de semiconductores altamente avanzados que se utilizan para implementar dispositivos CMOS. La polarización de la celda se codifica como posición de carga y las interacciones de puntos cuánticos dependen del acoplamiento electrostático. Sin embargo, los procesos de semiconductores actuales aún no han llegado a un punto en el que sea posible la producción en masa de dispositivos con características tan pequeñas (≈20 nanómetros). Sin embargo, los métodos litográficos en serie hacen que la implementación de QCA de estado sólido sea alcanzable, pero no necesariamente práctica. La litografía en serie es lenta, costosa e inadecuada para la producción en masa de dispositivos QCA de estado sólido. Hoy en día, la mayoría de los experimentos de creación de prototipos de QCA se realizan utilizando esta tecnología de implementación.

Un método propuesto pero aún no implementado consiste en construir dispositivos QCA a partir de moléculas individuales. Las ventajas esperadas de este método incluyen: estructura celular QCA altamente simétrica, velocidades de conmutación muy altas, densidad de dispositivos extremadamente alta, operación a temperatura ambiente e incluso la posibilidad de producir dispositivos en masa mediante autoensamblaje. Aún quedan por resolver una serie de desafíos técnicos, incluida la elección de moléculas, el diseño de mecanismos de interconexión adecuados y la tecnología de sincronización antes de que este método pueda implementarse.

La QCA magnética, comúnmente denominada MQCA (o QCA: M), se basa en la interacción entre nanopartículas magnéticas. El vector de magnetización de estas nanopartículas es análogo al vector de polarización en todas las demás implementaciones. En MQCA, el término "cuántico" se refiere a la naturaleza mecánico-cuántica de las interacciones de intercambio magnético y no a los efectos de tunelización de electrones. Los dispositivos construidos de esta manera podrían funcionar a temperatura ambiente.

La tecnología de semiconductores complementarios de óxido metálico (CMOS) ha sido el estándar de la industria para la implementación de dispositivos integrados a muy gran escala (VLSI) durante las últimas cuatro décadas, principalmente debido a las consecuencias de la miniaturización de dichos dispositivos (es decir, aumento de las velocidades de conmutación, aumento de la complejidad y disminución del consumo de energía). Los autómatas celulares cuánticos (QCA) son solo una de las muchas tecnologías alternativas propuestas como solución de reemplazo a los límites fundamentales que impondrá la tecnología CMOS en los próximos años.

Aunque el QCA resuelve la mayoría de las limitaciones de la tecnología CMOS, también aporta las suyas propias. Las investigaciones sugieren que el tiempo de conmutación intrínseco de una celda QCA es, en el mejor de los casos, del orden de los terahercios. Sin embargo, la velocidad real puede ser mucho menor, del orden de los megahercios para el QCA de estado sólido y de los gigahercios para el QCA molecular, debido a la configuración adecuada de la frecuencia de conmutación del reloj cuasi-adiabático.

• Debashis De, Sitanshu Bhattacharaya y K. P. Ghatak, Quantum Dots and Quantum Cellular Automata: Recent Trends and Applications, Nova, 2013
• Srivastava, S.; Asthana, A.; Bhanja, S.; Sarkar, S., "QCAPro - Una herramienta de estimación de la potencia de error para el diseño del circuito de QCA", en Circuitos y Sistemas (ISCAS), 2011 IEEE International Symposium on, vol., no., pp. 2377-2380, 15-18 May 2011
• V.V. Zhirnov, R.K. Cavin, J.A. Hutchby, y G.I. Bourianoff, “Limits to binario logic switch scaling—A gedanken model,” Proc. IEEE, vol. 91, p. 1934, Nov. 2003.
• S. Bhanja, y S. Sarkar, “Probabilistic Modeling of QCA Circuits using Bayesian Networks”, IEEE Transactions on Nanotechnology, Vol. 5(6), p. 657-670, 2006.
• S. Srivastava, y S. Bhanja, “Hierarchical Probabilistic Macromodeling for QCA Circuits”, IEEE Transactions on Computers, Vol. 56(2), p. 174-190, Feb. 2007.
• Beth, T. Proceedings. “Computación cuántica: una introducción” El Simposio Internacional IEEE 2000 sobre circuitos y sistemas, 2000. May 2000 p. 735-736 vol.1
• Victor V. Zhirnov, James A. Hutchby, George I. Bourianoff y Joe E. Brewer “Emerging Research Logic Devices” IEEE Circuits " Devices Magazine mayo 2005 p. 4
• Wolfram, Stephen “A New Kind of Science”, Wolfram Media May, 2002 p. ix (Prefacio)
• C.S. Lent, P. Tougaw, W. Porod y G. Bernstein, “Quantum cellular automata” Nanotechnology, vol. 4, 1993 p. 49-57.
• Victor V. Zhirnov, James A. Hutchby, George I. Bourianoff y Joe E. Brewer “Emerging Research Logic Devices” IEEE Circuits " Devices Magazine mayo 2005 p. 7
• Konrad Walus y G. A. Jullien “Quantum-Dot Cellular Automata Adders” Departamento de Electrical & Computer Eng. University of Calgary Calgary, AB, Canada p. 4 - 6
• S. Henderson, E. Johnson, J. Janulis y D. Tougaw, “Incorporating standard CMOS process methodologies into the QCA logic design process” IEEE Trans. Nanotechnology, vol. 3, no. 1, mar. 2004. págs. 2 a 9
• Christopher Graunke, David Wheeler, Douglas Tougaw, Jeffreay D. Will. “Aplicación de una red de barras cruzadas utilizando automata celular de puntos cuánticos” IEEE Transacciones sobre Nanotecnología, vol. 4, no 4, Jul. 2005 p. 1 - 6
• G. T ́oth y C. S. Lent, “Quasiadiabatic Switching for metal-island quantum-dot cellular automata”, Journal of Applied Physics, vol. 85, no. 5, 1999 p. 2977 - 2984
• G. T ́oth, C. S. Lent, “Quantum computing with quantum-dot cellular automata”, Física Rev. A, vol. 63, 2000 págs. 1 a 9
• C. S. Lent, B. Isaksen, M. Lieberman, “Molecular Quantum-Dot Cellular Automata”, J. Am. Chem. Soc., vol. 125, 2003 p. 1056 - 1063
• K. Walus, G. A. Jullien, V. S. Dimitrov, “Computer Arithmetic Structures for Quantum Cellular Automata” Department of Electrical & Computer Eng. University of Calgary, Calgary, AB, Canada p. 1 - 4
• Rui Zhang, Pallav Gupta y Niraj K. Jha “Synthesis of Majority and Minority Networks and Its Applications to QCA, TPL and SET Based Nanotechnologies” Proceedings of the 18th International Conference on VLSI Design held jointly with 4th International Conference on Embedded Systems Design 2005 p. 229- 234
• Los primeros informes publicados que introducen el concepto de Quantum Automaton:
• Baianu, I. 1971a. "Categorías, Functores y Teoría de Automata Cuántica". El cuarto Intl. Congreso LMPS, agosto-sept.1971;
• Baianu, I.1971b. "Supercategorías orgánicas y dinámicas cualitativas de sistemas". Bull. Math. Biophys., 33 (339–353): http://cogprints.ecs.soton.ac.uk/archive/00003674/01/ORganismic_supercategories_and_qualitative_dynamics_of_systems_final3.pdf.
• Niemier, M. 2004. Diseño de Sistemas Digitales en Automata Celular Cuántica, tesis doctoral, Universidad de Notre Dame.
• Actualizaciones recientes:
• Automata reversible cuántica: http://cogprints.org/3697/
• Quantum Nano-Automata.: http://doc.cern.ch/archive/electronic/other/ext/ext-2004-125/Quantumnanoautomata.doc
• Categorías de Quantum Automata.: [1]

• [2] – Página de inicio de QCA en Notre Dame