Atractor de Rossler

El atractor de Rössler es el atractor del sistema de Rössler, un sistema de tres ecuaciones diferenciales ordinarias no lineales estudiado originalmente por Otto Rössler en la década de 1970. Estas ecuaciones diferenciales definen un sistema dinámico de tiempo continuo que exhibe una dinámica caótica asociada con las propiedades fractales del atractor. Rössler lo interpretó como una formalización de una máquina para sacar caramelos.

Algunas propiedades del sistema Rössler se pueden deducir a través de métodos lineales como eigenvectores, pero las características principales del sistema requieren métodos no lineales como mapas Poincaré y diagramas de bifurcación. El papel original de Rössler afirma que el atacante Rössler tenía la intención de comportarse de forma similar al atacante Lorenz, pero también ser más fácil de analizar cualitativamente. Una órbita dentro del receptor sigue una espiral externa cerca del ${\displaystyle x,y}$ avión alrededor de un punto fijo inestable. Una vez que el gráfico en espiral lo suficiente, un segundo punto fijo influye en el gráfico, causando un aumento y giro en el ${\displaystyle z}$- Dimensión. En el dominio del tiempo, se hace evidente que aunque cada variable oscila dentro de un rango fijo de valores, las oscilaciones son caóticas. Este atacante tiene algunas similitudes con el atacante Lorenz, pero es más sencillo y tiene sólo un doble. Otto Rössler diseñó el atacante Rössler en 1976, pero las ecuaciones teóricas originarias fueron encontradas más tarde para modelar el equilibrio en las reacciones químicas.

Definición

Las ecuaciones de definición del sistema Rössler son:

${\displaystyle {\begin{cases}{\frac {dx} {dt}=-y-z\\{\frac} {\fnh}=x+ay\\\\\fnMicroc {dz}=b+z(x-c)\end{cases}}$

Rössler estudió el atractivo caótico con ${\displaystyle a=0.2}$, ${\displaystyle b=0.2}$, y ${\displaystyle c=5.7}$, aunque propiedades de ${\displaystyle a=0.1}$, ${\displaystyle b=0.1}$, y ${\displaystyle c=14}$ han sido más utilizados desde entonces. Otra línea del espacio del parámetro fue investigada utilizando el análisis topológico. Corresponde a ${\displaystyle b=2}$, ${\displaystyle c=4}$, y ${\displaystyle a}$ fue elegido como parámetro de bifurcación. Cómo Rössler descubrió este conjunto de ecuaciones fue investigado por Letellier y Messager.

Análisis de estabilidad

Parte de la elegancia del atraedor Rössler se debe a que dos de sus ecuaciones son lineales; el ajuste ${\displaystyle z=0}$, permite examinar el comportamiento en el ${\displaystyle x,y}$ avión

${\displaystyle {\begin{cases}{\frac {dx} {dt}=-y\\{\frac} {}=x+ay\end{cases}}$

La estabilidad en la ${\displaystyle x,y}$ plano se puede encontrar entonces calculando los eigenvalues de los Jacobian ${\displaystyle {\begin{pmatrix}0 â\1 recura\\\\end{pmatrix}}}$, que son ${\displaystyle (a\pm {\sqrt {a^{2}-4}}/2}$. De esto, podemos ver eso cuando ${\displaystyle 0 realizadasa$, los eigenvalues son complejos y ambos tienen un componente real positivo, haciendo que el origen sea inestable con una espiral externa en el ${\displaystyle x,y}$ avión. Ahora considere ${\displaystyle z}$ comportamiento plano dentro del contexto de este rango para ${\displaystyle a}$. Mientras tanto ${\displaystyle x}$ es más pequeño que ${\displaystyle c}$, el ${\displaystyle c}$ el término mantendrá la órbita cerca ${\displaystyle x,y}$ avión. A medida que se aproxima la órbita ${\displaystyle x}$ más grande que ${\displaystyle c}$, el ${\displaystyle z}$- Los valores comienzan a subir. As ${\displaystyle z}$ escala, sin embargo, el ${\displaystyle -z}$ en la ecuación para ${\displaystyle dx/dt}$ detiene el crecimiento ${\displaystyle x}$.

Puntos fijos

Para encontrar los puntos fijos, las tres ecuaciones Rössler se fijan a cero y el (${\displaystyle x}$,${\displaystyle y}$,${\displaystyle z}$) coordenadas de cada punto fijo fueron determinadas por la resolución de las ecuaciones resultantes. Esto produce las ecuaciones generales de cada una de las coordenadas de punto fijo:

${\displaystyle {\begin{cases}x={\frac {c\pm {\sqrt {c^{2}-4ab}} {2}\\y=-\left({\frac}} {\c}} {\c}}}\\y=-\y=-\left({\frac} {\c} {\c} {\c}}} {\c}}}} {\c}}}}}}}}\\\y=\y=\y=\y=-\y=-\y=-\y=-\y=-\left({\left({\c} {\c}\c}\c} {\c}\c}\c}\c}\c}\c}\c}\c}\c}\c}\c}\c\c}\c}\c}\c}\c}\c}\c}\c}\c\c\c\c}\c}\c}\c}\c}\c}\c}\c}\c}\c\c}\c}\c}\c}\c}\c} {c\pm {\sqrt {c^{2}-4ab}} {2a}}\right)\z={\frac} {\fnMicroc}}}} {\c}}}}}}}}}}}\s={\c} {\c}\c} {\c}}}}}}}}}}}}}}}}\dere}\s=\s={\s={\s={\s={\c}\s=\s={\c}\c}\c}\c}\s={\c}\c}\c}\s={\c}\c}\c}\c}\c}\c}\c}\c}\c}\c}\c}\c}\c}\c}\c}\c}}\c}\c}\c}\c}\c}\c}\c}\c}}}}}\c}\c}\c}}\c}}\c}\c}}}}}}}}}}}}}\ {c\pm {\sqrt {C}4a {\fnMicrosoft Sans Serif}} {\fnMicrosoft Sans Serif}} {\fnMicrosoft Sans Serif}$

Lo cual a su vez se puede utilizar para mostrar los puntos fijos reales para un conjunto determinado de valores de parámetros:

${\displaystyle \left({\frac {c+{\sqrt {\fnMic {-c-{\sqrt {c^{2}-4ab}}}{2a}}}{2a}}}{\frac {c+{\sqrt}} {\sqrt}}}} {\fc}} {\fc}} {\fc\fc\\c\c\c\c\c\c\c\c\c\c\c\c\c\cH00}\c\c\c\cH00}\c\c\c\c\sqrt} {c^{2}-4ab}} {2a}\derecha)}$

${\displaystyle \left({\frac {c-{\sqrt {c}-4ab}}}{2}} {\frac {-c+{\sqrt {C}4a {\fnMicroc {c-{\sqrt} {c^{2}-4ab}} {2a}\derecha)}$

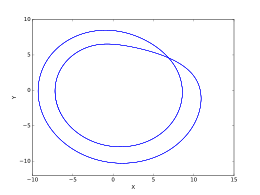
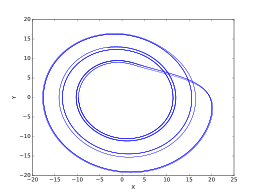
Como se muestra en los gráficos generales del atractor de Rössler anteriores, uno de estos puntos fijos reside en el centro del bucle del atractor y el otro se encuentra relativamente lejos del atractor.

Valores propios y vectores propios

La estabilidad de cada uno de estos puntos fijos se puede analizar determinando sus respectivos valores propios y vectores propios. Empezando por el jacobiano:

${\displaystyle {\begin{pmatrix}0 ventaja-1\1}}}}}$

Los valores propios se pueden determinar resolviendo la siguiente ecuación cúbica:

${\displaystyle -\lambda ^{3}+\lambda ^{2}(a+x-c)+\lambda (ac-ax-1-z)+x-c+az=0\,}$

Para el punto fijo ubicado centralmente, los valores de parámetros originales de Rössler de a=0,2, b=0,2 y c=5,7 producen valores propios de:

${\displaystyle \lambda _{1}=0.0971028+0.995786i\,}$

${\displaystyle \lambda _{2}=0.0971028-0.995786i\,}$

${\displaystyle \lambda ¿Qué?$

La magnitud de un valor propio negativo caracteriza el nivel de atracción a lo largo del vector propio correspondiente. De manera similar, la magnitud de un valor propio positivo caracteriza el nivel de repulsión a lo largo del vector propio correspondiente.

Los vectores propios correspondientes a estos valores propios son:

${\displaystyle v_{1}={\begin{pmatrix}0.7073\\\-0.07278-0.7032i\\\0.0042-0.0007i\\\\end{pmatrix}}$

${\displaystyle v_{2}={\begin{pmatrix}0.7073\\0.07278+0.7032i\\\0.0042+0.0007i\\\end{pmatrix}}$

${\displaystyle [V_{3}={\begin{pmatrix}0.1682\\\-0.0286\0.9853\\\\\\end{pmatrix}}}}$

Estos eigenvectores tienen varias implicaciones interesantes. Primero, los dos pares eigenvalue/eigenvector (${\displaystyle v_{1}$ y ${\displaystyle v_{2}$) son responsables de la diapositiva exterior constante que ocurre en el disco principal del receptor. El último par de eigenvalue/eigenvector está atrayendo a lo largo de un eje que recorre el centro del manifold y representa el movimiento z que ocurre dentro del receptor. Este efecto se demuestra aproximadamente con la siguiente figura.

La figura examina los eigenvectores de punto fijo central. La línea azul corresponde al receptor estándar Rössler generado con ${\displaystyle a=0.2}$, ${\displaystyle b=0.2}$, y ${\displaystyle c=5.7}$. El punto rojo en el centro de este atracción es ${\displaystyle FP_{1}$. La línea roja que intersecte ese punto fijo es una ilustración del plano de repulsión generado por ${\displaystyle v_{1}$ y ${\displaystyle v_{2}$. La línea verde es una ilustración de la atracción ${\displaystyle v_{3}$. La línea magenta se genera al retroceder a través del tiempo desde un punto en el atractivo eigenvector que está ligeramente por encima ${\displaystyle FP_{1}$ – ilustra el comportamiento de los puntos que se hacen completamente dominados por ese vector. Tenga en cuenta que la línea magenta casi toca el plano del receptor antes de ser arrastrado hacia arriba hacia el punto fijo; esto sugiere que la apariencia general y el comportamiento del atraedor Rössler es en gran parte un producto de la interacción entre el atractivo ${\displaystyle v_{3}$ y el replanteamiento ${\displaystyle v_{1}$ y ${\displaystyle v_{2}$ avión. Específicamente implica que una secuencia generada de las ecuaciones Rössler comenzará a bucle alrededor ${\displaystyle FP_{1}$, empezar a ser arrastrado hacia arriba en el ${\displaystyle v_{3}$ vector, creando el brazo ascendente de una curva que se dobla ligeramente hacia el vector antes de ser empujado hacia fuera de nuevo, ya que es tirado hacia el plano replanteador.

Para el punto fijo superior, los valores de parámetro originales de Rössler ${\displaystyle a=0.2}$, ${\displaystyle b=0.2}$, y ${\displaystyle c=5.7}$ eigenvalues de rendimiento de:

${\displaystyle \lambda _{1}=-0.0000046+5.4280259i}$

${\displaystyle \lambda _{2}=-0.0000046-5.4280259i}$

${\displaystyle \lambda ### {3}=0.1929830}$

Los vectores propios correspondientes a estos valores propios son:

${\displaystyle v_{1}={\begin{pmatrix}0.0002422+0.1872055i\0.0344403-0.0013136i\0.9817159\\\end{pmatrix}}$

${\displaystyle v_{2}={\begin{pmatrix}0.0002422-0.1872055i\0.0344403+0.0013136i\0.9817159\\\end{pmatrix}}$

${\displaystyle v_{3}={\begin{pmatrix}0.0049651\-0.7075770\0.7066188\\\\\end{pmatrix}}}}}$

Aunque estos eigenvalues y eigenvectores existen en el receptor Rössler, su influencia se limita a las iteraciones del sistema Rössler cuyas condiciones iniciales están en las inmediaciones generales de este punto fijo más remoto. Excepto en aquellos casos en que las condiciones iniciales se encuentran en el plano de atracción generado por ${\displaystyle \lambda ¿Qué?$ y ${\displaystyle \lambda _{2}$, esta influencia implica efectivamente empujar el sistema resultante hacia el receptor general Rössler. A medida que la secuencia resultante se acerca al punto fijo central y el propio atracción, la influencia de este punto fijo distante (y sus eigenvectores) se desvanecerá.

mapa de poincaré

El mapa de Poincaré se construye trazando el valor de la función cada vez que pasa a través de un plano establecido en una dirección específica. Un ejemplo sería trazar el ${\displaystyle y,z}$ valor cada vez que pasa a través de ${\displaystyle x=0}$ avión donde ${\displaystyle x}$ está cambiando de negativo a positivo, comúnmente hecho al estudiar el atractivo Lorenz. En el caso del atacante Rössler, el ${\displaystyle x=0}$ plano es ininteresante, ya que el mapa siempre cruza el ${\displaystyle x=0}$ avión ${\displaystyle z=0}$ debido a la naturaleza de las ecuaciones Rössler. En el ${\displaystyle x=0.1}$ avión ${\displaystyle a=0.1}$, ${\displaystyle b=0.1}$, ${\displaystyle c=14}$, el mapa de Poincaré muestra el aumento en ${\displaystyle z}$ valores ${\displaystyle x}$ aumenta, como es de esperarse debido a la sección de aumento y giro de la trama Rössler. El número de puntos en esta parcela específica Poincaré es infinito, pero cuando es diferente ${\displaystyle c}$ valor se utiliza, el número de puntos puede variar. Por ejemplo, con un ${\displaystyle c}$ valor de 4, sólo hay un punto en el mapa de Poincaré, porque la función produce una órbita periódica del período uno, o si la ${\displaystyle c}$ el valor se fija en 12.8, habría seis puntos correspondientes a un período de seis órbitas.

lorenz map

El mapa de Lorenz es la relación entre las máximas sucesivas de una coordenadas en una trayectoria. Considere una trayectoria en el atraccióndor, y dejemos ${\displaystyle x_{max}(n)}$ ser el máximo n-th de su x-coordinado. Entonces... ${\displaystyle x_{max}(n)}$-${\displaystyle x_{max}(n+1)}$ scatterplot es casi una curva, lo que significa que saber ${\displaystyle x_{max}(n)}$ uno puede casi exactamente predecir ${\displaystyle x_{max}(n+1)}$.

Mapeo de maxima local

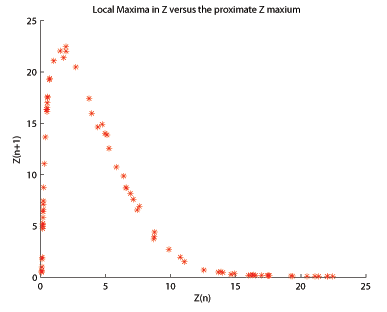
En el papel original sobre el atractivo Lorenz, Edward Lorenz analizó la máxima local ${\displaystyle z}$ contra la máxima local inmediatamente anterior. Cuando se visualizó, la parcela se asemejó al mapa de la tienda, lo que implica que se puede utilizar un análisis similar entre el mapa y el atracción. Para el atacante Rössler, cuando el ${\displaystyle z_{n}$ máximo local se trama contra el siguiente local ${\displaystyle z}$ máximo, ${\displaystyle z_{n+1}$, la trama resultante ${\displaystyle a=0.2}$, ${\displaystyle b=0.2}$, ${\displaystyle c=5.7}$) es unimodal, que se parece a un skewed Hénon mapa. Sabiendo que el atraccióndor Rössler puede ser utilizado para crear un mapa pseudo 1-d, entonces sigue para utilizar métodos de análisis similares. El diagrama de bifurcación es un método de análisis particularmente útil.

Variación de parámetros

El comportamiento de Rössler es en gran parte un factor de los valores de sus parámetros constantes ${\displaystyle a}$, ${\displaystyle b}$, y ${\displaystyle c}$. En general, variar cada parámetro tiene un efecto comparable haciendo que el sistema converge hacia una órbita periódica, punto fijo o escape hacia el infinito, sin embargo los rangos y comportamientos específicos inducidos varían sustancialmente para cada parámetro. Las órbitas periódicas, o "ciclos de unidad", del sistema Rössler se definen por el número de bucles alrededor del punto central que ocurre antes de que la serie de bucles comience a repetirse.

Los diagramas de bifurcación son una herramienta común para analizar el comportamiento de sistemas dinámicos, uno de los cuales es el atractor de Rössler. Se crean ejecutando las ecuaciones del sistema, manteniendo constantes todas las variables menos una y variando la última. Luego, se traza un gráfico de los puntos que visita un valor particular para la variable modificada después de que los factores transitorios han sido neutralizados. Las regiones caóticas se indican mediante regiones rellenas del gráfico.

Variando una

Aquí, ${\displaystyle b}$ se fija a 0.2, ${\displaystyle c}$ se fija en 5.7 y ${\displaystyle a}$ cambios. Examen numérico del comportamiento del atacante sobre el cambio ${\displaystyle a}$ sugiere que tiene una influencia desproporcionada sobre el comportamiento del atacante. Los resultados del análisis son:

• ${\displaystyle a\leq 0}$: Converges al punto fijo central
• ${\displaystyle a=0.1}$: Ciclo unitario del período 1
• ${\displaystyle a=0.2}$: Valor estándar del parámetro seleccionado por Rössler, caótico
• ${\displaystyle a=0.3}$: Atratador caótico, significativamente más parecido a la tira Möbius (plegándose sobre sí mismo).
• ${\displaystyle a=0.35}$: Similar a.3, pero cada vez más caótico
• ${\displaystyle a=0.38}$: Similar a.35, pero cada vez más caótico.

Variante b

Aquí, ${\displaystyle a}$ se fija a 0.2, ${\displaystyle c}$ se fija en 5.7 y ${\displaystyle b}$ cambios. Como se muestra en el diagrama adjunto, como ${\displaystyle b}$ enfoques 0 el receptor se acerca al infinito (nota el aumento de los valores muy pequeños ${\displaystyle b}$. Comparativo con los otros parámetros, variable ${\displaystyle b}$ genera un mayor rango cuando se producirán órbitas de período-3 y período 6. En contraste con ${\displaystyle a}$ y ${\displaystyle c}$, valores superiores de ${\displaystyle b}$ convergen al período-1, no a un estado caótico.

C variable

Aquí, ${\displaystyle a=b=0.1}$ y ${\displaystyle c}$ cambios. El diagrama de bifurcación revela que los valores bajos de ${\displaystyle c}$ son periódicos, pero rápidamente se vuelven caóticos como ${\displaystyle c}$ aumenta. Este patrón se repite como ${\displaystyle c}$ aumentos – hay secciones de periodicidad intercaladas con períodos de caos, y la tendencia es hacia órbitas de mayor duración como ${\displaystyle c}$ aumenta. Por ejemplo, el período de una órbita sólo aparece para valores ${\displaystyle c}$ alrededor de 4 y nunca se encuentra de nuevo en el diagrama de bifurcación. El mismo fenómeno se observa con el período tres; hasta ${\displaystyle c=12}$, período tres órbitas se pueden encontrar, pero después, no aparecen.

Una ilustración gráfica del atractivo cambiante sobre una gama de ${\displaystyle c}$ los valores ilustran el comportamiento general visto para todos estos análisis del parámetro – las frecuentes transiciones entre la periodicidad y la aperiodidad.

Varying c

c = 4, período 1

c = 6, período 2

c 8.5, período 4

c 8.7, período 8

c 9, caótico

c = 12, período 3

c 12.6, período 6

c = 13, caótica

c = 18, caótico

c = 15.4, período 5

El conjunto de imágenes anterior ilustra las variaciones del sistema de Rössler post-transiente como ${\displaystyle c}$ es variado sobre una gama de valores. Estas imágenes fueron generadas con ${\displaystyle a=b=.1}$.

• ${\displaystyle c=4}$Órbita del período 1.
• ${\displaystyle c=6}$órbita del período-2.
• ${\displaystyle c=8.5}$órbita del período 4.
• ${\displaystyle c=8.7}$órbita del período 8.
• ${\displaystyle c=9}$, escasa atracción caótica.
• ${\displaystyle c=12}$órbita del período 3.
• ${\displaystyle c=12.6}$órbita del período 6.
• ${\displaystyle c=13}$, escasa atracción caótica.
• ${\displaystyle c=15.4}$órbita del período 5.
• ${\displaystyle c=18}$Atacante caótico lleno.

órbitas periódicas

El receptor se llena densamente de órbitas periódicas: soluciones para las cuales existe un valor no cero de ${\displaystyle T}$ tales que ${\displaystyle {\vec {x}(t+T)={\vec {x}(t)}$. Estas soluciones interesantes pueden derivarse numéricamente usando el método de Newton. Las órbitas periódicas son las raíces de la función ${\displaystyle \Phi ¿Qué?$, donde ${\displaystyle ¿Qué?$ es la evolución por el tiempo ${\displaystyle t}$ y ${\displaystyle Id.$ es la identidad. A medida que la mayoría de las dinámicas ocurren en el plano x-y, las órbitas periódicas pueden entonces ser clasificadas por su número de viento alrededor del equilibrio central después de la proyección.

Tabla de Orbits Periódicos por Número de Viento k

k= 1

k = 2

k = 3

El tiempo no es escalar. Se utilizaron los parámetros originales (a,b,c) = (0.2,0.2,5.7).

Parece por experimentación numérica que existe una órbita periódica única para todos los números de devanado positivo. Esta falta de degeneración probablemente proviene de la falta de simetría del problema. El atractor se puede diseccionar en colectores invariantes más fáciles de digerir: órbitas periódicas 1D y los colectores 2D estables e inestables de órbitas periódicas. Estos colectores invariantes son un esqueleto natural del atractor, al igual que los números racionales son a los números reales.

Para los propósitos de la teoría de sistemas dinámicos, uno podría estar interesado en los invariantes topológicos de estos múltiples. Las órbitas periódicas son copias de ${\displaystyle S^{1}$ incrustado en ${\displaystyle \mathbb {R} } {}} {}displaystyle \mathbb {R} }$, por lo que sus propiedades topológicas se pueden entender con la teoría del nudo. Las órbitas periódicas con números de viento 1 y 2 forman un enlace Hopf, mostrando que ningún diffeomorfismo puede separar estas órbitas.

Enlaces a otros temas

Las bandas evidentes en el atractor de Rössler son similares a un conjunto de Cantor girado alrededor de su punto medio. Además, la media torsión que se produce en el atractor de Rössler sólo afecta a una parte del atractor. Rössler demostró que su atractor era en realidad la combinación de una "banda normal" y una tira de Möbius.