Átomo de hidrógeno
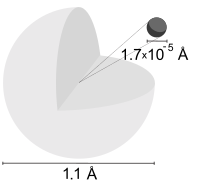
Un átomo de hidrógeno es un átomo del elemento químico hidrógeno. El átomo eléctricamente neutro contiene un solo protón cargado positivamente y un solo electrón cargado negativamente unido al núcleo por la fuerza de Coulomb. El hidrógeno atómico constituye aproximadamente el 75% de la masa bariónica del universo.
En la vida cotidiana en la Tierra, los átomos de hidrógeno aislados (llamados "hidrógeno atómico") son extremadamente raros. En cambio, un átomo de hidrógeno tiende a combinarse con otros átomos en compuestos, o con otro átomo de hidrógeno para formar hidrógeno gaseoso ordinario (diatómico), H2. "Hidrógeno atómico" y "átomo de hidrógeno" en el uso ordinario del inglés tienen significados superpuestos, pero distintos. Por ejemplo, una molécula de agua contiene dos átomos de hidrógeno, pero no contiene hidrógeno atómico (que se referiría a átomos de hidrógeno aislados).
La espectroscopia atómica muestra que existe un conjunto discreto e infinito de estados en los que puede existir un átomo de hidrógeno (o cualquier otro), en contra de las predicciones de la física clásica. Los intentos de desarrollar una comprensión teórica de los estados del átomo de hidrógeno han sido importantes para la historia de la mecánica cuántica, ya que todos los demás átomos pueden entenderse de manera aproximada conociendo en detalle esta estructura atómica más simple.
Isótopos
El isótopo más abundante, hidrógeno-1, protio o hidrógeno ligero, no contiene neutrones y es simplemente un protón y un electrón. El protio es estable y constituye el 99,985 % de los átomos de hidrógeno naturales.
El deuterio contiene un neutrón y un protón en su núcleo. El deuterio es estable y constituye el 0,0156 % del hidrógeno natural y se utiliza en procesos industriales como reactores nucleares y resonancia magnética nuclear.
El tritio contiene dos neutrones y un protón en su núcleo y no es estable, se descompone con una vida media de 12,32 años. Debido a su corta vida media, el tritio no existe en la naturaleza excepto en pequeñas cantidades.
Los isótopos de hidrógeno más pesados solo se crean artificialmente en aceleradores de partículas y tienen vidas medias del orden de 10−22 segundos. Son resonancias no unidas ubicadas más allá de la línea de goteo de neutrones; esto resulta en la pronta emisión de un neutrón.
Las fórmulas a continuación son válidas para los tres isótopos de hidrógeno, pero se deben usar valores ligeramente diferentes de la constante de Rydberg (fórmula de corrección que se proporciona a continuación) para cada isótopo de hidrógeno.
Ion de hidrógeno
Los átomos de hidrógeno neutros solitarios son raros en condiciones normales. Sin embargo, el hidrógeno neutro es común cuando está unido covalentemente a otro átomo, y los átomos de hidrógeno también pueden existir en formas catiónicas y aniónicas.
Si un átomo de hidrógeno neutro pierde su electrón, se convierte en un catión. El ion resultante, que consiste únicamente en un protón para el isótopo habitual, se escribe como "H+" ya veces llamado hydron. Los protones libres son comunes en el medio interestelar y el viento solar. En el contexto de las soluciones acuosas de los ácidos clásicos de Brønsted-Lowry, como el ácido clorhídrico, en realidad se trata de hidronio, H3O+. En lugar de que se forme un solo átomo de hidrógeno ionizado literal, el ácido transfiere el hidrógeno a H2O, formando H3O+.
Si, en cambio, un átomo de hidrógeno gana un segundo electrón, se convierte en un anión. El anión de hidrógeno se escribe como "H–" y llamado hidruro.
Análisis teórico
El átomo de hidrógeno tiene un significado especial en la mecánica cuántica y la teoría cuántica de campos como un sistema físico simple de problemas de dos cuerpos que ha producido muchas soluciones analíticas simples en forma cerrada.
Descripción clásica fallida
Los experimentos realizados por Ernest Rutherford en 1909 demostraron que la estructura del átomo era un núcleo denso y positivo con una tenue nube de carga negativa a su alrededor. Esto inmediatamente planteó preguntas sobre cómo un sistema de este tipo podría ser estable. El electromagnetismo clásico había demostrado que cualquier carga acelerada irradia energía, como lo muestra la fórmula de Larmor. Si se supone que el electrón orbita en un círculo perfecto e irradia energía continuamente, el electrón entraría en espiral rápidamente en el núcleo con un tiempo de caída de:
Modelo de Bohr-Sommerfeld
En 1913, Niels Bohr obtuvo los niveles de energía y las frecuencias espectrales del átomo de hidrógeno después de hacer una serie de suposiciones simples para corregir el fallido modelo clásico. Los supuestos incluían:
- Los electrones sólo pueden estar en ciertas órbitas circulares discretas o Estados fijos, teniendo así un conjunto discreto de posibles radios y energías.
- Los electrones no emiten radiación mientras que en uno de estos estados estacionarios.
- Un electrón puede ganar o perder energía saltando de una órbita discreta a otra.
Bohr supuso que el momento angular del electrón está cuantificado con valores posibles:
Para n=1{displaystyle n=1}, el valor
El valor exacto de la constante de Rydberg supone que el núcleo tiene una masa infinita con respecto al electrón. Para hidrógeno-1, hidrógeno-2 (deuterio) e hidrógeno-3 (tritio) que tienen masa finita, la constante debe modificarse ligeramente para usar la masa reducida del sistema, en lugar de simplemente la masa del electrón. Esto incluye la energía cinética del núcleo en el problema, porque la energía cinética total (electrón más nuclear) es equivalente a la energía cinética de la masa reducida que se mueve con una velocidad igual a la velocidad del electrón relativa al núcleo. Sin embargo, dado que el núcleo es mucho más pesado que el electrón, la masa del electrón y la masa reducida son casi las mismas. La constante de Rydberg RM para un átomo de hidrógeno (un electrón), R viene dada por
Todavía había problemas con el modelo de Bohr:
- no pudo predecir otros detalles espectrales tales como estructura fina y estructura hiperfinada
- sólo podría predecir niveles de energía con cualquier precisión para los átomos de un solo electrón (hidrógeno como átomos)
- los valores predichos sólo eran correctos α α 2.. 10− − 5{displaystyle alpha ^{2}approx 10^{-5}, donde α α {displaystyle alpha } es la constante de buena estructura.
La mayoría de estas deficiencias se resolvieron mediante la modificación del modelo de Bohr por parte de Arnold Sommerfeld. Sommerfeld introdujo dos grados de libertad adicionales, permitiendo que un electrón se mueva en una órbita elíptica caracterizada por su excentricidad y declinación con respecto a un eje elegido. Esto introdujo dos números cuánticos adicionales, que corresponden al momento angular orbital y su proyección en el eje elegido. Por lo tanto, se encontró la multiplicidad correcta de estados (excepto por el factor 2 que explica el espín del electrón aún desconocido). Además, al aplicar la relatividad especial a las órbitas elípticas, Sommerfeld logró derivar la expresión correcta para la estructura fina de los espectros de hidrógeno (que resulta ser exactamente la misma que en la teoría de Dirac más elaborada). Sin embargo, algunos fenómenos observados, como el efecto Zeeman anómalo, quedaron sin explicación. Estos problemas se resolvieron con el pleno desarrollo de la mecánica cuántica y la ecuación de Dirac. A menudo se alega que la ecuación de Schrödinger es superior a la teoría de Bohr-Sommerfeld para describir el átomo de hidrógeno. Este no es el caso, ya que la mayoría de los resultados de ambos enfoques coinciden o son muy parecidos (una notable excepción es el problema del átomo de hidrógeno en campos eléctricos y magnéticos cruzados, que no puede resolverse de forma coherente en el marco de la teoría de Bohr). teoría de Sommerfeld), y en ambas teorías las principales deficiencias resultan de la ausencia del espín del electrón. Fue el fracaso total de la teoría de Bohr-Sommerfeld para explicar los sistemas de muchos electrones (como el átomo de helio o la molécula de hidrógeno) lo que demostró su insuficiencia para describir los fenómenos cuánticos.
Ecuación de Schrödinger
La ecuación de Schrödinger permite calcular los estados estacionarios y también la evolución temporal de los sistemas cuánticos. Las respuestas analíticas exactas están disponibles para el átomo de hidrógeno no relativista. Antes de ir a presentar una cuenta formal, aquí damos una visión general elemental.
Dado que el átomo de hidrógeno contiene un núcleo y un electron, la mecánica cuántica permite predecir la probabilidad de encontrar el electrón a cualquier distancia radial dada r{displaystyle r}. Es dada por el cuadrado de una función matemática conocida como la "función de onda", que es una solución de la ecuación Schrödinger. El estado de equilibrio energético más bajo del átomo de hidrógeno es conocido como el estado del suelo. La función de onda del estado de tierra se conoce como 1s{displaystyle 1mathrm} función de onda. Está escrito como:
Aquí, a0{displaystyle A_{0} es el valor numérico del radio Bohr. La densidad de probabilidad de encontrar el electrón a distancia r{displaystyle r} en cualquier dirección radial es el valor cuadrado de la función de onda:
El 1s{displaystyle 1mathrm} la función de onda es simétrica esférica, y la superficie de una concha a distancia r{displaystyle r} es 4π π r2{displaystyle 4pi r^{2}, así que la probabilidad total P()r)dr{displaystyle P(r),dr} el electron estando en una concha a una distancia r{displaystyle r} y espesor dr{displaystyle dr} es
Resulta que esto es un máximo r=a0{displaystyle R=a_{0}. Es decir, la imagen Bohr de un electrón orbitando el núcleo en el radio a0{displaystyle A_{0} corresponde al radio más probable. En realidad, hay una probabilidad finita de que el electrón pueda ser encontrado en cualquier lugar r{displaystyle r}, con el probabilidad indicada por el cuadrado de la función de onda. Desde la probabilidad de encontrar el electrón en alguna parte en todo el volumen es unidad, la integral de P()r)dr{displaystyle P(r),dr} es unidad. Entonces decimos que la función de onda es normalizada.
Como se describe a continuación, el estado del suelo 1s{displaystyle 1mathrm} también se indica por los números cuánticos ()n=1,l l =0,m=0){displaystyle (n=1,ell =0,m=0)}. Los segundos estados de energía más bajos, justo por encima del estado del suelo, son dados por los números cuánticos ()2,0,0){displaystyle (2,0,0)}, ()2,1,0){displaystyle (2,1,0)}, y ()2,1,± ± 1){displaystyle (2,1,pm 1)}. Éstos n=2{displaystyle n=2} todos los estados tienen la misma energía y son conocidos como 2s{displaystyle 2mathrm} y 2p{displaystyle 2mathrm {p} estados. Hay uno 2s{displaystyle 2mathrm} estado:
Un electron en el 2s{displaystyle 2mathrm} o 2p{displaystyle 2mathrm {p} el estado es más probable que se encuentre en la segunda órbita Bohr con energía dada por la fórmula Bohr.
Función de onda
El Hamiltoniano del átomo de hidrógeno es el operador de energía cinética radial y la fuerza de atracción de Coulomb entre el protón positivo y el electrón negativo. Usando la ecuación de Schrödinger independiente del tiempo, ignorando todas las interacciones de spin-coupling y utilizando la masa reducida μ μ =meM/()me+M){displaystyle mu =m_{e}M/(m_{e}+M)}, la ecuación está escrita como:
Expandiendo el Laplaciano en coordenadas esféricas:
Esta es una ecuación diferencial separable y parcial que se puede resolver en términos de funciones especiales. Cuando la función de onda se separa como producto de funciones R()r){displaystyle R(r)}, .. ()Silencio Silencio ){displaystyle Theta (theta)}, y CCPR CCPR ()φ φ ){displaystyle Phi (varphi)} tres funciones diferenciales independientes aparecen con A y B siendo las constantes de separación:
- radial: ddr()r2dRdr)+2μ μ r2▪ ▪ 2()E+e24π π ε ε 0r)R− − AR=0{displaystyle {frac}left(r^{2}{frac} {fnK} {fnMicroc {2m} {hbar ^{2}}}left(E+{frac} {fnMicroc}} {fnMicroc}} {fnMicroc}}}}}}}}}left(E+{m} {fnMicroc} {f}}} {f} {f}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}m}}}}}}}}m}}}}}}m}m}m}m}m}m}m}}}}}}}}}m}m}m}m}}}}}}}}}}}}}}}}}}}} {fnK}{4pi} "varepsilon"
- polar: pecado Silencio Silencio .. ddSilencio Silencio ()pecado Silencio Silencio d.. dSilencio Silencio )+Apecado2 Silencio Silencio − − B=0{displaystyle {frac {sin theta {Theta} {frac {dtheta}left(sin theta {frac {dTheta }{dtheta}}right)+Asin ^{2}theta -B=0}
- azimuth: 1CCPR CCPR d2CCPR CCPR dφ φ 2+B=0.{fnMicroc} {1}{2} {fnK} {fnK}} {fnK}} {fnK}} {fnK} {f} {fn}} {fnK}} {fnK}}} {fn} {f}}} {f} {f}fnKf} {f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fnKf}f}f}f}f}f}f}f}f}fnKfnKf}f}f}fnKf}f}f}f}f Phi }{dvarphi ^{2}+ B=0.}
Las funciones de onda de posición normalizadas, dadas en coordenadas esféricas, son:
donde:
- *** *** =2rna0Alternativa Alternativa {displaystyle rho = {2r over {na_{0} {}}}},
- a0Alternativa Alternativa {displaystyle A_{0} {} {}} es el radio Bohr reducido, a0Alternativa Alternativa =4π π ε ε 0▪ ▪ 2μ μ e2{displaystyle a_{0} {={4pivarepsilon _{0}hbar ^{2}over {mu e^{2}}}},
- Ln− − l l − − 12l l +1()*** *** ){displaystyle L_{n-ell -1}{2ell +1}(rho)} es un polinomio de grado generalizado de Laguerre n− − l l − − 1{displaystyle n-ell -1}, y
- Yl l m()Silencio Silencio ,φ φ ){displaystyle Y_{ell } {thetavarphi)} es una función armónica esférica del grado l l {displaystyle ell } y orden m{displaystyle m}. Tenga en cuenta que los polinomios Laguerre generalizados son definidos de manera diferente por diferentes autores. El uso aquí es consistente con las definiciones utilizadas por el Mesías, y Mathematica. En otros lugares, el polinomio Laguerre incluye un factor ()n+l l )!{displaystyle (n+ell)}, o el polinomio Laguerre generalizado que aparece en la función de onda de hidrógeno es Ln+l l 2l l +1()*** *** ){displaystyle L_{n+ell }{2ell +1}(rho)} en su lugar.
Los números cuánticos pueden tomar los siguientes valores:
- n=1,2,3,...... {displaystyle n=1,2,3,ldots } (número cuántico principal)
- l l =0,1,2,...... ,n− − 1{displaystyle ell =0,1,2,ldotsn-1} (número cuántico nazimutal)
- m=− − l l ,...... ,l l {displaystyle m=-ellldotsell } (número cuántico magnético).
Además, estas funciones de onda están normalizadas (es decir, la integral de su módulo cuadrado es igual a 1) y ortogonales:
Las funciones de onda en el espacio de momento están relacionadas con las funciones de onda en el espacio de posición a través de una transformada de Fourier
Las soluciones a la ecuación de Schrödinger para el hidrógeno son analíticas, dando una expresión simple para los niveles de energía del hidrógeno y, por lo tanto, las frecuencias de las líneas espectrales del hidrógeno y reprodujeron completamente el modelo de Bohr y lo superaron. También produce otros dos números cuánticos y la forma de la función de onda del electrón ('orbital') para los diversos estados mecánico-cuánticos posibles, lo que explica el carácter anisotrópico de los enlaces atómicos.
La ecuación de Schrödinger también se aplica a átomos y moléculas más complicados. Cuando hay más de un electrón o núcleo, la solución no es analítica y se necesitan cálculos por computadora o se deben hacer suposiciones simplificadoras.
Dado que la ecuación de Schrödinger solo es válida para la mecánica cuántica no relativista, las soluciones que arroja para el átomo de hidrógeno no son del todo correctas. La ecuación de Dirac de la teoría cuántica relativista mejora estas soluciones (ver más abajo).
Resultados de la ecuación de Schrödinger
La solución de la ecuación Schrödinger (ecuación de onda) para el átomo de hidrógeno utiliza el hecho de que el potencial Coulomb producido por el núcleo es isotrópico (es radialmente simétrico en el espacio y sólo depende de la distancia al núcleo). Aunque la energía resultante eigenfunctions (las orbitales) no son necesariamente isotrópicos ellos mismos, su dependencia de las coordenadas angulares sigue completamente generalmente de esta isotropía del potencial subyacente: los eigentales del Hamiltonian (es decir, los eigenstates de energía) pueden ser elegidos como eigenstates simultáneos del operador de impulso angular. Esto corresponde al hecho de que el impulso angular se conserva en el movimiento orbital del electrón alrededor del núcleo. Por lo tanto, los eigentales energéticos pueden clasificarse por dos números cuánticos de impulso angular, l l {displaystyle ell } y m{displaystyle m} (ambos son enteros). Número cuántico de impulso angular l l =0,1,2,...... {displaystyle ell =0,1,2,ldots } determina la magnitud del impulso angular. Número de cuántico magnético m=− − l l ,...... ,+l l {displaystyle m=-ellldots+ell } determina la proyección del impulso angular en el (arbitraramente elegido) z{displaystyle z}-Eje.
Además de expresiones matemáticas para el impulso angular total y proyección angular de las funciones de onda, se debe encontrar una expresión para la dependencia radial de las funciones de onda. Es sólo aquí que los detalles de los 1/r{displaystyle 1/r} El potencial de Coulomb entra (dejando polinomios de Laguerre en r{displaystyle r}). Esto lleva a un tercer número cuántico, el principal número cuántico n=1,2,3,...... {displaystyle n=1,2,3,ldots }. El número cuántico principal en hidrógeno está relacionado con la energía total del átomo.
Tenga en cuenta que el valor máximo del número cuántico del impulso angular está limitado por el número cuántico principal: sólo puede funcionar hasta n− − 1{displaystyle n-1}, es decir, l l =0,1,...... ,n− − 1{displaystyle ell =0,1,ldotsn-1}.
Debido a la conservación del impulso angular, estados del mismo l l {displaystyle ell } pero diferente m{displaystyle m} tienen la misma energía (esto sostiene para todos los problemas con la simetría rotacional). Además, para el átomo de hidrógeno, estados del mismo n{displaystyle n} pero diferente l l {displaystyle ell } son también degenerados (es decir, tienen la misma energía). Sin embargo, se trata de una propiedad específica de hidrógeno y ya no es verdad para átomos más complicados que tienen un potencial (efectivo) diferente de la forma 1/r{displaystyle 1/r} (debido a la presencia de los electrones internos que protegen el potencial del núcleo).
Teniendo en cuenta el giro del electrón añade un último número cuántico, la proyección del impulso angular de giro del electrón a lo largo del z{displaystyle z}-eje, que puede asumir dos valores. Por lo tanto, cualquier eigensta del electrón en el átomo de hidrógeno se describe completamente por cuatro números cuánticos. Según las reglas usuales de la mecánica cuántica, el estado actual del electrón puede ser cualquier superposición de estos estados. Esto explica también por qué la elección de z{displaystyle z}-eje para la cuantificación direccional del vector de impulso angular es inmaterial: un orbital de dado l l {displaystyle ell } y m.{displaystyle m'} obtenido para otro eje preferido z.{displaystyle z} siempre puede ser representado como una superposición adecuada de los diversos estados de diferentes m{displaystyle m} (pero el mismo) l l {displaystyle ell }) que se han obtenido para z{displaystyle z}.
Resumen matemático de estados propios del átomo de hidrógeno
En 1928, Paul Dirac encontró una ecuación que era totalmente compatible con la relatividad especial y (como consecuencia) convirtió la función de onda en un "espinor de Dirac" de 4 componentes. incluyendo "arriba" y "abajo" componentes de espín, tanto positivos como "negativos" energía (o materia y antimateria). La solución a esta ecuación dio los siguientes resultados, más precisos que la solución de Schrödinger.
Niveles de energía
Los niveles de energía del hidrógeno, incluida la estructura fina (excluyendo el desplazamiento de Lamb y la estructura hiperfina), vienen dados por la expresión de estructura fina de Sommerfeld:
Estados coherentes
Los estados coherentes se han propuesto como
Visualización de los orbitales de electrones de hidrógeno
La imagen de la derecha muestra los primeros orbitales del átomo de hidrógeno (funciones propias de energía). Estas son secciones transversales de la densidad de probabilidad que están codificadas por colores (el negro representa la densidad cero y el blanco representa la densidad más alta). El número cuántico de momento angular (orbital) ℓ se indica en cada columna, utilizando el código de letras espectroscópico habitual (s significa ℓ = 0, p significa ℓ = 1, d significa ℓ = 2). El número cuántico principal (principal) n (= 1, 2, 3,...) está marcado a la derecha de cada fila. Para todas las imágenes, el número cuántico magnético m se ha establecido en 0, y el plano de la sección transversal es el plano xz (z es el eje vertical). La densidad de probabilidad en el espacio tridimensional se obtiene girando la que se muestra aquí alrededor del eje z.
El "estado fundamental", es decir, el estado de menor energía, en el que normalmente se encuentra el electrón, es el primero, el estado 1s (nivel cuántico principal n = 1, ℓ = 0).
Las líneas negras aparecen en todos los orbitales excepto en el primero: estos son los nodos de la función de onda, es decir, donde la densidad de probabilidad es cero. (Más precisamente, los nodos son armónicos esféricos que aparecen como resultado de resolver la ecuación de Schrödinger en coordenadas esféricas).
Los números cuánticos determinan el diseño de estos nodos. Hay:
- n− − 1{displaystyle n-1} nodos totales,
- l l {displaystyle ell } de los cuales son nodos angulares:
- m{displaystyle m} los nodos angulares rodean φ φ {displaystyle varphi } axis (en el xy avión). (La figura anterior no muestra estos nodos ya que trama secciones transversales a través de los xz-plane.)
- l l − − m{displaystyle ell -m} (los nodos angulares restantes) ocurren en Silencio Silencio {displaystyle theta } Axis.
- n− − l l − − 1{displaystyle n-ell -1} (los nodos no-angulares restantes) son nodos radiales.
Características que van más allá de la solución de Schrödinger
Hay varios efectos importantes que la ecuación de Schrödinger ignora y que son responsables de ciertas desviaciones pequeñas pero medibles de las líneas espectrales reales de las predichas:
- Aunque la velocidad media del electrón en hidrógeno es sólo 1/137 de la velocidad de la luz, muchos experimentos modernos son suficientemente precisos que una explicación teórica completa requiere un tratamiento totalmente relativista del problema. Un tratamiento relativista resulta en un aumento de impulso de aproximadamente 1 parte en 37.000 para el electrón. Dado que la longitud de onda del electrón está determinada por su impulso, las órbitas que contienen electrones de velocidad superior muestran contracción debido a longitudes de onda más pequeñas.
- Incluso cuando no hay campo magnético externo, en el marco inercial del electrón en movimiento, el campo electromagnético del núcleo tiene un componente magnético. El giro del electrón tiene un momento magnético asociado que interactúa con este campo magnético. Este efecto también se explica por la relatividad especial, y conduce a la llamada acoplamientos de giro-orbito, es decir, una interacción entre el movimiento orbital del electrón alrededor del núcleo, y su giro.
Estas dos características (y más) están incorporadas en la ecuación relativista de Dirac, con predicciones que se acercan aún más a la experimentación. De nuevo, la ecuación de Dirac puede resolverse analíticamente en el caso especial de un sistema de dos cuerpos, como el átomo de hidrógeno. Los estados cuánticos de solución resultantes ahora deben clasificarse por el número de momento angular total j (que surge del acoplamiento entre el espín del electrón y el momento angular orbital). Los estados del mismo j y del mismo n aún están degenerados. Por lo tanto, la solución analítica directa de la ecuación de Dirac predice 2S(1/2) y 2P(1/2) niveles de hidrógeno para tener exactamente la misma energía, lo que está en contradicción con observaciones (experimento de Lamb-Retherford).
- Siempre hay fluctuaciones de vacío del campo electromagnético, según la mecánica cuántica. Debido a tales fluctuaciones degeneración entre estados de la misma j pero diferente l es levantado, dándoles energías ligeramente diferentes. Esto se ha demostrado en el famoso experimento Lamb-Retherford y fue el punto de partida para el desarrollo de la teoría de la electrodinámica cuántica (que es capaz de lidiar con estas fluctuaciones de vacío y emplea los famosos diagramas Feynman para aproximaciones utilizando la teoría de la perturbación). Este efecto se llama turno de cordero.
Para estos desarrollos, era esencial que la solución de la ecuación de Dirac para el átomo de hidrógeno pudiera resolverse exactamente, de modo que cualquier desviación observada experimentalmente debía tomarse en serio como una señal de falla de la teoría.
Alternativas a la teoría de Schrödinger
En el lenguaje de la mecánica matricial de Heisenberg, Wolfgang Pauli resolvió por primera vez el átomo de hidrógeno usando una simetría rotacional en cuatro dimensiones [simetría O(4)] generada por el momento angular y el vector de Laplace-Runge-Lenz. Extendiendo el grupo de simetría O(4) al grupo dinámico O(4,2), todo el espectro y todas las transiciones estaban integrados en una única representación de grupo irreductible.
En 1979, el átomo de hidrógeno (no relativista) se resolvió por primera vez dentro de la formulación de la integral de trayectoria de Feynman. de la mecánica cuántica de Duru y Kleinert. Este trabajo amplió en gran medida el rango de aplicabilidad del método de Feynman.
Libros
- Griffiths, David J. (1995). Introducción a la Mecánica Cuántica. Prentice Hall. ISBN 0-13-111892-7. La sección 4.2 trata específicamente el átomo de hidrógeno, pero todo el capítulo 4 es relevante.
- Kleinert, H. (2009). Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 4a edición, Worldscibooks.com, World Scientific, Singapur (también disponible en línea physik.fu-berlin.de)
Contenido relacionado
Ácido tartárico
Difluoruro de radón
Ácido gamma-hidroxibutírico










































![{displaystyle -{frac {hbar ^{2}}{2mu }}left[{frac {1}{r^{2}}}{frac {partial }{partial r}}left(r^{2}{frac {partial psi }{partial r}}right)+{frac {1}{r^{2}sin theta }}{frac {partial }{partial theta }}left(sin theta {frac {partial psi }{partial theta }}right)+{frac {1}{r^{2}sin ^{2}theta }}{frac {partial ^{2}psi }{partial varphi ^{2}}}right]-{frac {e^{2}}{4pi varepsilon _{0}r}}psi =Epsi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fed150abb1693ab2493937b669446a54865b9562)







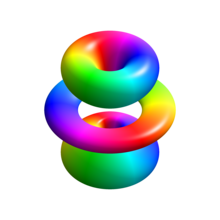






























![{displaystyle {begin{aligned}E_{j,n}={}&-mu c^{2}left[1-left(1+left[{frac {alpha }{n-j-{frac {1}{2}}+{sqrt {left(j+{frac {1}{2}}right)^{2}-alpha ^{2}}}}}right]^{2}right)^{-1/2}right]\approx {}&-{frac {mu c^{2}alpha ^{2}}{2n^{2}}}left[1+{frac {alpha ^{2}}{n^{2}}}left({frac {n}{j+{frac {1}{2}}}}-{frac {3}{4}}right)right],end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e54f0064eafaeab9e7d8b3e5e41e667a3138a7b)




![{displaystyle {begin{aligned}langle r,thetavarphi mid s,gamma{bar {Omega }}rangle ={}&e^{-s^{2}/2}sum _{n=0}^{infty }(s^{n}e^{igamma /(n+1)^{2}}/{sqrt {n!}})\&{}times ,sum _{ell =0}^{n}u_{n+1}^{ell }(r)sum _{m=-ell }^{ell }left[{frac {(2ell)!}{(ell +m)!(ell -m)!}}right]^{1/2}left(sin {frac {bar {theta }}{2}}right)^{ell -m}left(cos {frac {bar {theta }}{2}}right)^{ell +m}\&{}times ,e^{-i(m{bar {varphi }}+ell {bar {psi }})}Y_{ell m}(thetavarphi){sqrt {2ell +1}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb48ff266b61e92b9bdfcd39d562729c3910e97a)



