Ataque de cumpleaños

A Ataque de cumpleaños es un tipo de ataque criptográfico que explota las matemáticas detrás del problema del cumpleaños en la teoría de probabilidad. Este ataque se puede utilizar para abusar de la comunicación entre dos o más partes. El ataque depende de la mayor probabilidad de colisiones encontradas entre intentos de ataque al azar y un grado fijo de permutaciones (pigeonholes). Con un ataque de cumpleaños, es posible encontrar una colisión de una función de hash en 2n=2n/2{fnK}}=2n/2}, con 2n{textstyle 2^{n} ser la seguridad clásica de la preimage. Hay un resultado general (aunque disputado) que las computadoras cuánticas pueden realizar ataques de cumpleaños, rompiendo así la resistencia a la colisión, en 2n3=2n/3{fn}=2^{n/3}.

Aunque existen algunas vulnerabilidades de firma digital asociadas con el ataque de cumpleaños, no se puede usar para romper un esquema de encriptación más rápido que un ataque de fuerza bruta.

Comprender el problema

Comparación del problema de cumpleaños (1) y ataque de cumpleaños (2):

En (1), las colisiones se encuentran dentro de un set, en este caso, 3 de 276 pares de los 24 astronautas lunares.

En (2), las colisiones se encuentran entre dos conjuntos, en este caso, 1 de 256 emparejamientos de sólo los primeros bytes de SHA-256 hashes de 16 variantes cada uno de contratos benignos y maliciosos.

Como ejemplo, considere el escenario en el que un profesor con una clase de 30 estudiantes (n = 30) pide el cumpleaños de todos (por simplicidad, ignorar los años bisiestos) para determinar si alguno de los dos estudiantes tiene el mismo cumpleaños (correspondiendo a una colisión precipitada como se describe más adelante). Intuitivamente, esta oportunidad puede parecer pequeña. Contra-intuitivamente, la probabilidad de que al menos un estudiante tenga el mismo cumpleaños que cualquiera otro estudiante en cualquier día es alrededor del 70% (por n = 30), de la fórmula 1− − 365!()365− − n)!⋅ ⋅ 365n{displaystyle 1-{frac {365}{(365-n)}cdot 365^{n}}}}.

Si el maestro hubiera elegido un específico día (por ejemplo, 16 de septiembre), entonces la posibilidad de que al menos un estudiante naciera en ese día específico es 1− − ()364/365)30{displaystyle 1-(364/365)}{30}, alrededor del 7,9%.

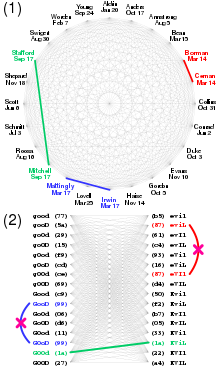
En un ataque de cumpleaños, el atacante prepara muchas variantes diferentes de contratos benignos y maliciosos, cada uno con una firma digital. Se busca un par de contratos benignos y maliciosos con la misma firma. En este ejemplo ficticio, suponga que la firma digital de una cadena es el primer byte de su hash SHA-256. El par encontrado se indica en verde; tenga en cuenta que encontrar un par de contratos benignos (azul) o un par de contratos maliciosos (rojo) es inútil. Después de que la víctima acepta el contrato benigno, el atacante lo sustituye por el malicioso y afirma que la víctima lo firmó, como lo prueba la firma digital.

Matemáticas

Dada la función f{displaystyle f}, el objetivo del ataque es encontrar dos entradas diferentes x1,x2{displaystyle x_{1},x_{2}} tales que f()x1)=f()x2){displaystyle f(x_{1}=f(x_{2}}. Un par así. x1,x2{displaystyle x_{1},x_{2}} se llama colisión. El método utilizado para encontrar una colisión es simplemente para evaluar la función f{displaystyle f} para diferentes valores de entrada que pueden ser elegidos aleatoriamente o seudorandualmente hasta que el mismo resultado se encuentra más de una vez. Debido al problema del cumpleaños, este método puede ser bastante eficiente. Específicamente, si una función f()x){displaystyle f(x)} cede cualquiera de H{displaystyle H. diferentes productos con igual probabilidad y H{displaystyle H. es suficientemente grande, entonces esperamos obtener un par de argumentos diferentes x1{displaystyle x_{1}} y x2{displaystyle x_{2} con f()x1)=f()x2){displaystyle f(x_{1}=f(x_{2}} después de evaluar la función para 1.25H{displaystyle 1.25{sqrt {H}} diferentes argumentos en promedio.

Consideramos el siguiente experimento. De un conjunto de valores H, elegimos valores n uniformemente al azar, lo que permite repeticiones. Sea p(n; H) la probabilidad de que durante este experimento se elija al menos un valor más de una vez. Esta probabilidad se puede aproximar como

p()n;H).. 1− − e− − n()n− − 1)/()2H).. 1− − e− − n2/()2H){displaystyle p(n;H)approx 1-e^{-n(n-1)/(2H)}approx 1-e^{-n^{2}/(2H)}}

Sea n(p; H) el menor número de valores que tenemos para elegir, tal que la probabilidad de encontrar una colisión es al menos p. Al invertir esta expresión anterior, encontramos la siguiente aproximación

n()p;H).. 2HIn⁡ ⁡ 11− − p{displaystyle n(p;H)approx {fnMicroc} {1} {1-p}}}}

y asignando una probabilidad de colisión de 0,5 llegamos a

n()0.5;H).. 1.1774H{displaystyle n(0.5;H)approx 1.1774{sqrt {H}}

Sea Q(H) el número esperado de valores que tenemos que elegir antes de encontrar la primera colisión. Este número se puede aproximar por

Q()H).. π π 2H{displaystyle Q(H)approx {fnMicroc} ♪ - Sí.

Como ejemplo, si se usa un hash de 64 bits, hay aproximadamente 1.8×10¹⁹ salidas diferentes. Si todos estos son igualmente probables (el mejor de los casos), entonces se necesitaría 'solo' aproximadamente 5 mil millones de intentos (5.38×10⁹) para generar una colisión usando fuerza bruta. Este valor se denomina límite de cumpleaños y para códigos de n bits podría aproximarse a 2^n/2. Otros ejemplos son los siguientes:

Bits	Posibles productos (H)	Probabilidad deseada de colisión aleatoria (2 s.f.) (p)
		10−18	10−15	10−12	10−9	10−6	0,1%	1%	25%	50%	75%
16	216 (~6.5 x 104)	.	.	.	.	.	11	36	190	300	430
32	232 #4.3×109)	.	.	.	3	93	2900	9300	50.000	77.000	110.000
64	264 #1.8×1019)	6	190	6100	190.000	6.100.000	1.9×108	6.1×108	3.3×109	5.1×109	7.2×109
128	2128 #3.4×1038)	2.6×1010	8.2×1011	2.6×1013	8.2×1014	2.6×1016	8.3×1017	2.6×1018	1.4×1019	2.2×1019	3.1×1019
256	2256 #1.2×1077)	4.8×1029	1,5×1031	4.8×1032	1,5×1034	4.8×1035	1,5×1037	4.8×1037	2.6×1038	4.0×1038	5.7×1038
384	2384 #3.9×10115)	8.9×1048	2.8×1050	8.9×1051	2.8×1053	8.9×1054	2.8×1056	8.9×1056	4.8×1057	7.4×1057	1.0×1058
512	2512 #1.3×10154)	1.6×1068	5.2×1069	1.6×1071	5.2×1072	1.6×1074	5.2×1075	1.6×1076	8.8×1076	1.4×1077	1.9×1077

Tabla muestra número de hashes n()p) necesario para lograr la probabilidad dada del éxito, asumiendo que todos los hashes son igualmente probables. Para comparación, 10⁻¹⁸ a 10⁻¹⁵ es la tasa de error poco corregible de un disco duro típico. En teoría, MD5 hashes o UUIDs, siendo aproximadamente 128 bits, deben permanecer dentro de ese rango hasta unos 820 mil millones de documentos, incluso si sus posibles salidas son muchos más.

Es fácil ver que si las salidas de la función se distribuyen de forma desigual, entonces se puede encontrar una colisión incluso más rápido. La noción de "balance" de una función de hash cuantifica la resistencia de la función a los ataques de cumpleaños (explotando una distribución de clave desigual). Sin embargo, determinar el equilibrio de una función de hash normalmente requerirá que todos los insumos posibles sean calculados y por lo tanto es infeasible para las funciones de hash populares como las familias MD y SHA. La subexpresión In⁡ ⁡ 11− − p{displaystyle ln {frac {1}{1-p}} en la ecuación para n()p;H){displaystyle n(p;H)} no se calcula con precisión para pequeños p{displaystyle p} cuando se traduce directamente en idiomas comunes de programación log(1/(1-p)) debido a la pérdida de significado. Cuando log1p está disponible (como está en C99), por ejemplo, la expresión equivalente -log1p(-p) debería ser usado en su lugar. Si esto no se hace, la primera columna de la tabla anterior se calcula como cero, y varios elementos en la segunda columna no tienen ni siquiera un dígito significativo correcto.

Aproximación sencilla

Una buena regla general que se puede utilizar para el cálculo mental es la relación

p()n).. n22H{displaystyle p(n)approx {n^{2} over 2H}

que también se puede escribir como

H.. n22p()n){displaystyle Happrox {n^{2} over 2p(n)}.

o

n.. 2H× × p()n){displaystyle napprox {sqrt {2Htimes p(n)}}.

Esto funciona bien para probabilidades menores o iguales a 0,5.

Este esquema de aproximación es especialmente fácil de usar cuando se trabaja con exponentes. Por ejemplo, suponga que usted está construyendo hahes de 32 bits (H=232{displaystyle H=2^{32}) y quiere que la oportunidad de una colisión sea a la mayoría de un millón (p.. 2− − 20{displaystyle papprox 2^{-20}), ¿cuántos documentos podríamos tener más?

n.. 2× × 232× × 2− − 20=21+32− − 20=213=26.5.. 90,5{fnMicrosoft Sans Serif}={1+32-20}={sqrt [2^{13}=2^{6.5}approx 90.5}

que está cerca de la respuesta correcta de 93.

Susceptibilidad de la firma digital

Las firmas digitales pueden ser susceptibles a un ataque de cumpleaños. Un mensaje m{displaystyle m} se firma normalmente por primera computación f()m){displaystyle f(m)}, donde f{displaystyle f} es una función de hash criptográfico, y luego usar una clave secreta para firmar f()m){displaystyle f(m)}. Supongamos que Mallory quiere engañar a Bob para firmar un contrato fraudulento. Mallory prepara un contrato justo m{displaystyle m} y una fraudulenta m.{displaystyle m'}. Ella entonces encuentra una serie de posiciones donde m{displaystyle m} se puede cambiar sin cambiar el significado, como insertar comas, líneas vacías, uno contra dos espacios después de una frase, reemplazar sinónimos, etc. Al combinar estos cambios, puede crear un gran número de variaciones en m{displaystyle m} que son contratos justos.

De manera similar, Mallory también crea un gran número de variaciones en el contrato fraudulento m.{displaystyle m'}. A continuación, aplica la función hash a todas estas variaciones hasta que encuentre una versión del contrato justo y una versión del contrato fraudulento que tenga el mismo valor hash, f()m)=f()m.){displaystyle f(m)=f(m)}. Presenta la versión justa a Bob para firmar. Después de que Bob haya firmado, Mallory toma la firma y la adjunta al contrato fraudulento. Esta firma entonces "prueba" que Bob firmó el contrato fraudulento.

Las probabilidades difieren ligeramente del problema original del cumpleaños, ya que Mallory no gana nada encontrando dos contratos justos o dos fraudulentos con el mismo hash. La estrategia de Mallory es generar pares de un contrato justo y fraudulento. Las ecuaciones de problemas de cumpleaños se aplican donde n{displaystyle n} es el número de pares. El número de hashes Mallory realmente genera es 2n{displaystyle 2n}.

Para evitar este ataque, la longitud de salida de la función hash utilizada para un esquema de firma se puede elegir lo suficientemente grande como para que el ataque de cumpleaños se vuelva computacionalmente inviable, es decir, aproximadamente el doble de bits que los necesarios para evitar una fuerza bruta ordinaria. ataque.

Además de usar una longitud de bits mayor, el firmante (Bob) puede protegerse haciendo algunos cambios aleatorios e inofensivos en el documento antes de firmarlo y conservando una copia del contrato que firmó en su poder, de modo que puede al menos demostrar ante el tribunal que su firma coincide con ese contrato, no solo con el fraudulento.

El algoritmo rho de Pollard para logaritmos es un ejemplo de un algoritmo que usa un ataque de cumpleaños para el cálculo de logaritmos discretos.

Ataque inverso

El mismo fraude es posible si el firmante es Mallory, no Bob. Bob podría sugerirle un contrato a Mallory para que lo firme. Mallory podría encontrar una versión modificada de manera inofensiva de este contrato justo que tiene la misma firma que un contrato fraudulento, y Mallory podría proporcionar el contrato justo modificado y la firma a Bob. Más tarde, Mallory podría producir la copia fraudulenta. Si Bob no tiene el contrato de la versión modificada de manera inofensiva (quizás solo encuentre su propuesta original), el fraude de Mallory es perfecto. Si Bob lo tiene, Mallory al menos puede afirmar que es Bob el estafador.