Asignación latente de Dirichlet

En el procesamiento del lenguaje natural, la asignación de Dirichlet latente (LDA) es una red bayesiana (y, por lo tanto, un modelo estadístico generativo) para modelar temas extraídos automáticamente en corpus textuales. La LDA es un ejemplo de un modelo de tópicos bayesiano. En este, las observaciones (por ejemplo, palabras) se recopilan en documentos y la presencia de cada palabra es atribuible a uno de los tópicos del documento. Cada documento contendrá una pequeña cantidad de tópicos.

En el contexto de la genética de poblaciones, el LDA fue propuesto por J. K. Pritchard, M. Stephens y P. Donnelly en 2000.

David Blei, Andrew Ng y Michael I. Jordan aplicaron LDA en el aprendizaje automático en 2003.

En biología evolutiva y biomedicina, el modelo se utiliza para detectar la presencia de variación genética estructurada en un grupo de individuos. El modelo supone que los alelos que portan los individuos en estudio tienen su origen en varias poblaciones actuales o pasadas. El modelo y varios algoritmos de inferencia permiten a los científicos estimar las frecuencias de los alelos en esas poblaciones de origen y el origen de los alelos que portan los individuos en estudio. Las poblaciones de origen se pueden interpretar ex post en términos de varios escenarios evolutivos. En los estudios de asociación, la detección de la presencia de estructura genética se considera un paso preliminar necesario para evitar la confusión.

En la investigación en psicología clínica, el LDA se ha utilizado para identificar temas comunes de autoimágenes que experimentan los jóvenes en situaciones sociales. Otros científicos sociales han utilizado el LDA para examinar grandes conjuntos de datos temáticos de debates en las redes sociales (por ejemplo, tuits sobre medicamentos recetados).

En el contexto de la musicología computacional, el LDA se ha utilizado para descubrir estructuras tonales en diferentes corpus.

Una aplicación de LDA en el aprendizaje automático (específicamente, el descubrimiento de temas, un subproblema del procesamiento del lenguaje natural) es descubrir temas en una colección de documentos y luego clasificar automáticamente cualquier documento individual dentro de la colección en términos de su "relevancia" para cada uno de los temas descubiertos. Se considera que un tema es un conjunto de términos (es decir, palabras o frases individuales) que, en conjunto, sugieren un tema compartido.

Por ejemplo, en una colección de documentos relacionada con animales domésticos, los términos perro, spaniel, beagle, golden retriever, cachorro, ladrido y guau sugerirían un tema relacionado con PERRO, mientras que los términos gato, siamés, maine coon, atigrado, manx, miau, ronroneo y gatito sugerirían un tema relacionado con GATO. Puede haber muchos más temas en la colección (por ejemplo, relacionados con la dieta, el aseo, la atención médica, el comportamiento, etc.) que no analizamos para simplificar. (Las palabras vacías muy comunes en un idioma, por ejemplo, "the", "an", "that", "are", "is", etc., no discriminan entre temas y, por lo general, se filtran mediante el preprocesamiento antes de que se realice el LDA. El preprocesamiento también convierte los términos a sus formas léxicas "raíz"; por ejemplo, "barks", "barking" y "barked" se convertirían en "bark".)

Si la colección de documentos es lo suficientemente grande, LDA descubrirá dichos conjuntos de términos (es decir, temas) basándose en la coocurrencia de términos individuales, aunque la tarea de asignar una etiqueta significativa a un tema individual (es decir, que todos los términos estén relacionados con DOG) depende del usuario y, a menudo, requiere conocimientos especializados (por ejemplo, para la recopilación de documentos técnicos). El enfoque LDA supone que:

1. El contenido semántico de un documento está compuesto por combinar uno o más términos de uno o más temas.
2. Ciertos términos ambiguo, perteneciente a más de un tema, con diferente probabilidad. (Por ejemplo, el término Capacitación puede aplicarse tanto a perros como a gatos, pero son más propensos a referirse a perros, que se utilizan como animales de trabajo o participan en concursos de obediencia o habilidad.) Sin embargo, en un documento, la presencia adjunta de específico términos vecinos (que pertenecen a un solo tema) desambiguarán su uso.
3. La mayoría de los documentos contendrán sólo un número relativamente pequeño de temas. En la colección, por ejemplo, los temas individuales ocurrirán con frecuencias diferentes. Es decir, tienen una distribución de probabilidad, por lo que un documento dado es más probable que contenga algunos temas que otros.
4. Dentro de un tema, ciertos términos se utilizarán con mucha más frecuencia que otros. En otras palabras, los términos dentro de un tema también tendrán su propia distribución de probabilidad.

Cuando se emplea el aprendizaje automático LDA, ambos conjuntos de probabilidades se calculan durante la fase de entrenamiento, utilizando métodos bayesianos y un algoritmo de maximización de expectativas.

LDA es una generalización del enfoque anterior del análisis semántico latente probabilístico (pLSA). El modelo pLSA es equivalente a LDA bajo una distribución previa de Dirichlet uniforme. El pLSA se basa únicamente en los dos primeros supuestos anteriores y no se ocupa del resto. Si bien ambos métodos son similares en principio y requieren que el usuario especifique la cantidad de temas que se descubrirán antes del inicio del entrenamiento (como con la agrupación de K-medias), LDA tiene las siguientes ventajas sobre pLSA:

• La LDA produce una mejor desambiguación de palabras y una asignación más precisa de documentos a temas.
• Las probabilidades de computación permiten un proceso "generativo" mediante el cual se puede generar una colección de nuevos "documentos sintéticos" que reflejen de cerca las características estadísticas de la colección original.
• A diferencia de la LDA, el pLSA es vulnerable a la superposición, especialmente cuando aumenta el tamaño del cuerpo.
• El algoritmo LDA es más fácilmente recomendable para escalar para conjuntos de datos grandes utilizando el enfoque MapReduce en un clúster de cálculo.

Con la notación de placas, que se utiliza a menudo para representar modelos gráficos probabilísticos (PGM), las dependencias entre las distintas variables se pueden capturar de forma concisa. Los cuadros son "placas" que representan réplicas, que son entidades repetidas. La placa exterior representa documentos, mientras que la placa interior representa las posiciones de palabras repetidas en un documento determinado; cada posición está asociada con una elección de tema y palabra. Los nombres de las variables se definen de la siguiente manera:

M denota el número de documentos

N es número de palabras en un documento dado (documento i tiene ${\displaystyle N_{i}$ palabras)

α es el parámetro del Dirichlet anterior sobre las distribuciones de temas por documento

β es el parámetro del Dirichlet anterior en la distribución de palabras por tema

${\displaystyle \theta _{i}$ es la distribución de temas para el documento i

${\displaystyle \varphi _{k}$ es la distribución de palabras para el tema k

${\displaystyle z_{ij}}$ es el tema para el j-la palabra en el documento i

${\displaystyle w_{ij}$ es la palabra específica.

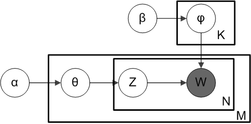
El hecho de que W se grayed significa que las palabras ${\displaystyle w_{ij}$ son las únicas variables observables, y las otras variables son variables latentes. Como se propone en el papel original, un Dirichlet anterior escaso se puede utilizar para modelar la distribución del tema-palabra, siguiendo la intuición de que la distribución de probabilidad sobre las palabras en un tema es segado, de modo que sólo un pequeño conjunto de palabras tienen alta probabilidad. El modelo resultante es la variante más ampliamente aplicada de la LDA hoy. La notación de placa para este modelo se muestra a la derecha, donde ${\displaystyle K}$ denota el número de temas y ${\displaystyle \varphi _{1},\dots\varphi ¿Qué?$ son ${\displaystyle V}$- vectores dimensionales que almacenan los parámetros de las distribuciones de palabras temáticas distribuidas por Dirichlet (${\displaystyle V}$ es el número de palabras en el vocabulario).

Es útil pensar en las entidades representadas por ${\displaystyle \theta }$ y ${\displaystyle \varphi }$ como matrices creadas por la descomposición de la matriz original de la palabra documento que representa el corpus de documentos que se están modelando. A este respecto, ${\displaystyle \theta }$ consta de filas definidas por documentos y columnas definidas por temas, mientras ${\displaystyle \varphi }$ consiste en filas definidas por temas y columnas definidas por palabras. Así, ${\displaystyle \varphi _{1},\dots\varphi ¿Qué?$ se refiere a un conjunto de filas, o vectores, cada uno de los cuales es una distribución sobre palabras, y ${\displaystyle \theta _{1},\dots\theta ¿Qué?$se refiere a un conjunto de filas, cada una de las cuales es una distribución sobre temas.

Para realmente inferir los temas en un corpus, imaginamos un proceso generativo por el cual se crean los documentos, para que podamos inferir, o ingeniería inversa, él. Imaginamos el proceso generativo como sigue. Los documentos están representados como mezclas aleatorias sobre temas latentes, donde cada tema se caracteriza por una distribución sobre todas las palabras. LDA asume el siguiente proceso generativo para un corpus ${\displaystyle D}$ consistente en ${\displaystyle M}$ documentos de cada longitud ${\displaystyle N_{i}$:

1. Elija ${\displaystyle \theta _{i}\sim \operatorname {Dir} (\alpha)}$, donde ${\displaystyle i\in \{1,\dots M\}}$ y ${\displaystyle \mathrm {Dir} (\alpha)}$ es una distribución Dirichlet con un parámetro simétrico ${\displaystyle \alpha }$ que normalmente es escasa (${\displaystyle \alpha .$)

2. Elija ${\displaystyle \varphi _{k}\sim \operatorname {Dir} (\beta)}$, donde ${\displaystyle k\in \{1,\dotsK}}$ y ${\displaystyle \beta }$ típicamente escaso

3. Para cada una de las posiciones ${\displaystyle i,j}$, donde ${\displaystyle i\in \{1,\dots M\}}$, y ${\displaystyle j\in \{1,\dotsN_{i}}}$

a) Elija un tema ${\displaystyle z_{i,j}\sim \operatorname {Multinomial} (\theta _{i}).}$

b) Elige una palabra ${\displaystyle w_{i,j}\sim \operatorname {Multinomial} (\varphi _{z_{i,j}).}$

(Tenga en cuenta que aquí la distribución multinomial se refiere a la distribución multinomial con un solo ensayo, que también se conoce como distribución categórica).

Las longitudes ${\displaystyle N_{i}$ son tratados como independientes de todas las otras variables generadoras de datos (${\displaystyle w}$ y ${\displaystyle z}$). El subscripto se deja caer a menudo, como en los diagramas de placa que se muestran aquí.

Una descripción formal de LDA es la siguiente:

Definición de variables en el modelo

Variable	Tipo	Significado
${\displaystyle K}$	entero	Número de temas (por ejemplo, 50)
${\displaystyle V}$	entero	número de palabras en el vocabulario (por ejemplo 50.000 o 1.000.000)
${\displaystyle M}$	entero	Número de documentos
${\displaystyle N_{d=1\dots M}$	entero	número de palabras en el documento d
${\displaystyle N}$	entero	total de palabras en todos los documentos; suma de todas ${\displaystyle N_{d}$ valores, es decir. ${\displaystyle N=\sum ¿Qué?$
${\displaystyle \alpha _{k=1\dots K}$	positivo real	peso previo del tema k en un documento; generalmente lo mismo para todos los temas; normalmente un número inferior a 1, por ejemplo 0.1, para preferir las distribuciones de temas escasos, es decir, pocos temas por documento
${\displaystyle {\boldsymbol {\alpha }$	K- vector dimensional de reales positivos	colección de todos ${\displaystyle \alpha _{k}$ valores, vistos como un vector único
${\displaystyle \beta _{w=1\dots V}$	positivo real	peso previo de la palabra w en un tema; generalmente lo mismo para todas las palabras; normalmente un número mucho menos de 1, por ejemplo 0.001, para preferir fuertemente escasas distribuciones de palabras, es decir, pocas palabras por tema
${\displaystyle {\boldsymbol {\beta }$	V- vector dimensional de reales positivos	colección de todos ${\displaystyle \beta _{w}$ valores, vistos como un vector único
${\displaystyle \varphi _{k=1\dots K,w=1\dots V}$	probabilidad (número real entre 0 y 1)	probabilidad de palabra w en el tema k
${\displaystyle {\boldsymbol {\varphi} }_{k=1\dots K}$	V- vector dimensional de probabilidades, que debe sumar a 1	distribución de palabras en tema k
${\displaystyle \theta _{d=1\dots M,k=1\dots K}$	probabilidad (número real entre 0 y 1)	probabilidad de temas k en el documento d
${\displaystyle {\boldsymbol {\theta }_{d=1\dots M}$	K- vector dimensional de probabilidades, que debe sumar a 1	distribución de temas en el documento d
${\displaystyle z_{d=1\dots M,w=1\dots No.$	entero entre 1 y 1 K	identidad de tema de palabra w en el documento d
${\displaystyle \mathbf {Z}$	N- vector dimensional de enteros entre 1 y 1 K	identidad de tema de todas las palabras en todos los documentos
${\displaystyle w_{d=1\dots M,w=1\dots No.$	entero entre 1 y 1 V	identidad de palabra w en el documento d
${\displaystyle \mathbf}$	N- vector dimensional de enteros entre 1 y 1 V	identidad de todas las palabras en todos los documentos

Podemos entonces describir matemáticamente las variables aleatorias de la siguiente manera:

${\displaystyle {\begin{aligned}{\boldsymbol [\varfia] }_{k=1\dots ################################################################################################################################################################################################################################################################ }_{d=1\dots M}\sim \operatorname {Dirichlet} _{K}({\boldsymbol {\alpha }) \\z_{d=1\dots M,w=1\dots N_{d} limit\sim \operatorname {Categorical} ################################################################################################################################################################################################################################################################ #### {d}\w_{d=1\dots M,w=1\dots N_{d} limit\sim \operatorname {Categorical} ¿Qué? }_{z_{dw})\end{aligned}}$

El aprendizaje de las distintas distribuciones (el conjunto de temas, sus probabilidades de palabras asociadas, el tema de cada palabra y la combinación particular de temas de cada documento) es un problema de inferencia estadística.

El artículo original de Pritchard et al. utilizó una aproximación de la distribución posterior mediante simulación de Monte Carlo. La propuesta alternativa de técnicas de inferencia incluye el muestreo de Gibbs.

El artículo original de ML utilizó una aproximación bayesiana variacional de la distribución posterior.

Una optimización directa de la probabilidad con un algoritmo de relajación de bloques resulta ser una alternativa rápida al MCMC.

En la práctica, el número óptimo de poblaciones o temas no se conoce de antemano. Se puede estimar mediante la aproximación de la distribución posterior con el método Monte Carlo de cadena de Markov con saltos reversibles.

Otros enfoques alternativos incluyen la propagación de expectativas.

La investigación reciente se ha centrado en acelerar la inferencia de la asignación de Dirichlet latente para apoyar la captura de un número masivo de temas en un gran número de documentos. La ecuación de actualización del sampler colapsado de Gibbs mencionado en la sección anterior tiene una esparidad natural dentro de ella que se puede aprovechar. Intuitivamente, ya que cada documento sólo contiene un subconjunto de temas ${\displaystyle K_{d}$, y una palabra también sólo aparece en un subconjunto de temas ${\displaystyle K_{w}$, la ecuación de actualización anterior podría ser reescrita para tomar ventaja de esta espacidad.

${\displaystyle p(Z_{d,n}=k)\propto {\frac {\alpha \beta . No. }+{\frac {C_{k}\beta . No. ¿Qué? +C_{k}{d}) . No. }$

En esta ecuación, tenemos tres términos, de los cuales dos son escasos, y el otro es pequeño. Nosotros llamamos a estos términos ${\displaystyle a,b}$ y ${\displaystyle c}$ respectivamente. Ahora, si normalizamos cada término resumiendo todos los temas, obtenemos:

${\displaystyle A=\sum - ¿Qué? {\alpha \beta ♫ {C_{k} {\neg} No. }$

${\displaystyle B=\sum - ¿Qué? {C_{k} {d}\beta ♫ {C_{k} {\neg} No. }$

${\displaystyle C=\sum - ¿Qué? {C_{k} {w} {\fnMicrosoft Sans Serif} +C_{k}{d}) ♫ {C_{k} {\neg} No. }$

Aquí, podemos ver que ${\displaystyle B}$ es un resumen de los temas que aparecen en el documento ${\displaystyle d}$, y ${\displaystyle C}$ es también un resumen escaso de los temas que una palabra ${\displaystyle w}$ se asigna a todo el cuerpo. ${\displaystyle A}$ por otro lado, es denso pero debido a los pequeños valores de ${\displaystyle \alpha }$ " ${\displaystyle \beta }$, el valor es muy pequeño en comparación con los otros dos términos.

Ahora, mientras muestra un tema, si muestramos una variable aleatoria uniformemente desde ${\displaystyle s\sim U(s imper\mid A+B+C)}$Podemos comprobar en qué cubo aterriza nuestra muestra. Desde ${\displaystyle A}$ es pequeño, somos muy poco probables caer en este cubo; sin embargo, si caemos en este cubo, muestreando un tema toma ${\displaystyle O(K)}$ tiempo (igual que el original Collapsed Gibbs Sampler). Sin embargo, si caemos en los otros dos cubos, sólo necesitamos revisar un subconjunto de temas si guardamos un registro de los temas escasos. Un tema se puede probar del ${\displaystyle B}$ cubo en ${\displaystyle O(K_{d}}$ tiempo, y un tema se puede probar del ${\displaystyle C}$ cubo en ${\displaystyle O(K_{w}}$ tiempo donde ${\displaystyle K_{d}$ y ${\displaystyle K_{w}$ denota el número de temas asignados al documento actual y el tipo de palabra actual respectivamente.

Observe que después de muestrear cada tema, actualizar estos cubos es todo básico ${\displaystyle O(1)}$ operaciones aritméticas.

A continuación se derivan las ecuaciones para el muestreo colapsado de Gibbs, lo que significa ${\displaystyle \varphi }$s and ${\displaystyle \theta }$s se integrará. Para la simplicidad, en esta derivación se supone que todos los documentos tienen la misma longitud ${\displaystyle N_{}$. La derivación es igualmente válida si las longitudes del documento varían.

Según el modelo, la probabilidad total del modelo es:

${\displaystyle P({\boldsymbol {W},{\boldsymbol {Z}},{\boldsymbol {\theta },{\boldsymbol {\varphi }}};\alpha\beta)=\prod _{i=1} {K}P(\varphi _{i};\beta)\prod _{j=1}^{M}P(\theta _{j};\alpha)\prod ¿Por qué?$

donde las variables bold-font denotan la versión vectorial de las variables. Primero, ${\displaystyle {\boldsymbol {\varphi} }$ y ${\displaystyle {\boldsymbol {\theta }$ necesita ser integrado.

${\displaystyle {\begin{aligned} {\boldsymbol {Z},{\boldsymbol {W};\alpha\beta)=\int _{\boldsymbol {\Theta }\int _{\boldsymbol {\varphi }P({\boldsymbol {W},{\boldsymbol {Z}}},{\boldsymbol {\theta }},{\boldsymbol {\varphi }}}};\alpha\beta)\,d{\boldsymbol {\bu}}}}}}} {\b} }\,d{\boldsymbol {\theta }\={} {\= {\fnMicrosoft Sans Serif}\prod ¿Por qué? - ¿Qué? ¿Qué? ################################################################################################################################################################################################################################################################ }\prod _{j=1} {M}P(\theta) - ¿Por qué? ################################################################################################################################################################################################################################################################ {\fnMicrosoft Sans Serif}$

Todo el mundo ${\displaystyle \theta }$s son independientes entre sí y lo mismo para todos ${\displaystyle \varphi }$s. Así podemos tratar a cada uno ${\displaystyle \theta }$ y cada uno ${\displaystyle \varphi }$ por separado. Ahora nos centramos sólo en el ${\displaystyle \theta }$ parte.

${\displaystyle \int _{\boldsymbol {\theta }\prod _{j=1} {M}P(\theta) - ¿Por qué? ################################################################################################################################################################################################################################################################ }=\prod _{j=1} {M}\int _{\theta _{j}P(\theta _{j};\alpha)\prod _{t=1} {N}P(Z_{j,t}\mid \theta _{j})\,d\theta _{j}.}$

Podemos concentrarnos más en uno. ${\displaystyle \theta }$ como sigue:

${\displaystyle \int _{\theta ¿Por qué? _{t=1} {N}P(Z_{j,t}\mid \theta _{j})\,d\theta _{j}.}$

En realidad, es la parte oculta del modelo para el ${\displaystyle j^{th}$ documento. Ahora reemplazamos las probabilidades en la ecuación anterior por la verdadera expresión de distribución para escribir la ecuación explícita.

${\displaystyle \int _{\theta ¿Por qué? ################################################################################################################################################################################################################################################################ ¿Qué? {\Gamma \left(\sum ¿Por qué? ¿Qué? Gamma (\alpha _{i}}\prod ##{i=1} {K}\theta - ¿Qué? ################################################################################################################################################################################################################################################################ _{t=1} {N}P(Z_{j,t}\mid \theta _{j})\,d\theta _{j}.}$

Vamos. ${\displaystyle n_{j,r} {i}}$ ser el número de fichas de palabras en el ${\displaystyle j^{th}$ documento con la misma palabra símbolo (el ${\displaystyle r^{th}$ palabra en el vocabulario) asignado a ${\displaystyle i^{th}}$ Tema. Entonces, ${\displaystyle n_{j,r} {i}}$ es tridimensional. Si cualquiera de las tres dimensiones no se limita a un valor específico, utilizamos un punto paréntesis ${\displaystyle (\cdot)}$ a Denote. Por ejemplo, ${\displaystyle n_{j,(\cdot)}{i}$ denota el número de fichas de palabras en el ${\displaystyle j^{th}$ documento asignado al ${\displaystyle i^{th}}$ Tema. Así, la mayor parte de la ecuación anterior puede ser reescrita como:

${\displaystyle \prod _{t=1}{N}P(Z_{j,t}\mid \theta ¿Qué? ##{i=1} {K}\theta ¿Qué?$

Así que... ${\displaystyle \theta _{j}}$ la fórmula de integración se puede cambiar a:

${\displaystyle \int _{\theta ¿Qué? {\Gamma \left(\sum ¿Por qué? ¿Qué? Gamma (\alpha _{i}}\prod ##{i=1} {K}\theta - ¿Qué? ################################################################################################################################################################################################################################################################ ##{i=1} {K}\theta _{j,i}{n_{j,(\cdot)}\,d\theta _{j}=\int _{\theta ¿Qué? {\Gamma \left(\sum ¿Por qué? ¿Qué? Gamma (\alpha _{i}}\prod ##{i=1} {K}\theta ¿Por qué? ¿Por qué?$

La ecuación dentro de la integración tiene la misma forma que la distribución de Dirichlet. Según la distribución de Dirichlet,

${\displaystyle \int _{\theta ¿Qué? {\Gamma \left(\sum ¿Por qué? ¿Por qué? ##{i=1} {K}\theta ¿Por qué? - ¿Por qué?$

Por lo tanto,

${\displaystyle {\begin{aligned} _{\theta _{j}P(\theta _{j};\alpha)\prod ################################################################################################################################################################################################################################################################ ¿Qué? {\Gamma \left(\sum ¿Por qué? ¿Qué? Gamma (\alpha _{i}}\prod ##{i=1} {K}\theta ¿Por qué? ¿Por qué? {\Gamma \left(\sum ¿Por qué? ¿Qué? Gamma (\alpha _{i}} {\frac {\prod ¿Por qué? ¿Qué? {\Gamma \left(\sum ¿Por qué? ¿Por qué? ##{i=1} {K}\theta ¿Por qué? ¿Por qué? {\Gamma \left(\sum ¿Por qué? ¿Qué? Gamma (\alpha _{i}} {\frac {\prod ¿Por qué?$

Ahora ponemos nuestra atención a la ${\displaystyle {\boldsymbol {\varphi} }$ parte. En realidad, la derivación de la ${\displaystyle {\boldsymbol {\varphi} }$ parte es muy similar a la ${\displaystyle {\boldsymbol {\theta }$ parte. Aquí sólo enumeramos los pasos de la derivación:

${\displaystyle {\begin{aligned} ¿Qué? ¿Por qué? - ¿Qué? ¿Qué? ################################################################################################################################################################################################################################################################ }\[8pt]={} ¿Qué? - ¿Qué? - ¿Qué? ¿Qué? ################################################################################################################################################################################################################################################################ ¿Por qué? ¿Qué? ¿Qué? {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\f}} {\fnMicrosoft Sans Serif} "Gamma" _{i,r} {\beta ################################################################################################################################################################################################################################################################ ¿Por qué? ################################################################################################################################################################################################################################################################ ¿Qué? ¿Qué? {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\f}} {\fnMicrosoft Sans Serif} "Gamma" ¿Qué? ¿Qué? ################################################################################################################################################################################################################################################################ ################################################################################################################################################################################################################################################################ - ¿Qué? {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\f}} {\fnMicrosoft Sans Serif} ¿Por qué? ¿Por qué?$

Para la claridad, aquí escribimos la ecuación final con ambos ${\fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\\\\fnMicrosoft {\\\\fnMicrosoft {\\\\\fnMicrosoft {\\\\\\\fnMicrosoft {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ }$ y ${\displaystyle {\boldsymbol {\theta }$ integrado:

${\displaystyle P({\boldsymbol {Z},{\boldsymbol {W};\alpha\beta)=\prod ¿Por qué? {\Gamma \left(\sum ¿Por qué? ¿Qué? Gamma (\alpha _{i}} {\frac {\prod ¿Por qué? {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\f}} {\fnMicrosoft Sans Serif} ¿Por qué? ¿Por qué?$

El objetivo de Gibbs Sampling aquí es aproximar la distribución de ${\displaystyle P({\boldsymbol {Z}\mid {\boldsymbol {W};\alpha\beta)}$. Desde ${\displaystyle P({\boldsymbol {W};\alpha\beta)}$ es invariable para cualquiera de las ecuaciones Z, Gibbs Sampling puede derivarse de ${\displaystyle P({\boldsymbol {Z}},{\boldsymbol {W};\alpha\beta)}$ directamente. El punto clave es derivar la siguiente probabilidad condicional:

${\fnMicrosoft Sans Serif}, {\fnMicrosoft Sans Serif}},{\boldsymbol {W}};\alpha\beta)={\frac {m,n)},{\boldsymbol {Z_{-m,n)}}}}} {\boldsymbolds}}}}} {\m\bolds}}}}}}} {\f}} {\f}}}}}} {\f}}}}} {\f}} {\f}}}}}}}} {\f}}}}}}}}} {\f}}}}}}}}}}} {\f}}}}}}}}}}}}}}}}}}}}}}}}}}} {\m\m\m\m\m\f}}}}}}}}} {\m\m\m\bh}}} {\m\m\m\m\bh}}}}}}}} {W};\alpha\beta)}{\boldsymbol {Z_{-(m,n)}}}}},{\boldsymbol {W}}};\alpha\beta}}}}}}}}}$

Donde ${\displaystyle Z_{(m,n)}$ denota los ${\displaystyle Z}$ variable oculta de la ${\displaystyle n^{th}$ palabra token en el ${\displaystyle m^ {th}}$ documento. Y además asumimos que la palabra símbolo de ella es el ${\displaystyle v^{th}$ palabra en el vocabulario. ${\fnMicrosoft Sans Serif}}$ denota todos los ${\displaystyle Z}$s pero ${\displaystyle Z_{(m,n)}$. Tenga en cuenta que Gibbs Sampling sólo necesita para probar un valor para ${\displaystyle Z_{(m,n)}$, según la probabilidad anterior, no necesitamos el valor exacto

${\displaystyle P\left(Z_{m,n}\mid {\boldsymbol {Z_{-(m,n)}}}},{\boldsymbol {W}};\alpha\beta \right)}$

pero las relaciones entre las probabilidades que ${\displaystyle Z_{(m,n)}$ puede tomar valor. Así, la ecuación anterior se puede simplificar como:

${\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif}}}} {\fnMicrosoft Sans Serif} {\Gamma \left(\sum ¿Por qué? ¿Qué? Gamma (\alpha _{i}}} {M}\prod _{j\neq m}{\frac {\prod} ¿Por qué? Gamma \left(\sum ¿Por qué? {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\f}} {\fnMicrosoft Sans Serif} ¿Por qué? ¿Por qué? ¿Por qué? Gamma \left(\sum ¿Por qué? - ¿Qué? {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif}} {\fnMicrosoft Sans Serif} Gamma \left(\sum _{r=1}{V}n_{(\cdot),r}^{i}+\beta _{r}\right)}\[8pt] {\prod} ¿Por qué? Gamma \left(\sum ¿Por qué? - ¿Qué? {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif}} {\fnMicrosoft Sans Serif} Gamma \left(\sum _{r=1}{V}n_{(\cdot),r}^{i}+\beta _{r}\right)}\[8pt] ¿Por qué? - ¿Qué? {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif}} {\fnMicrosoft Sans Serif} Gamma \left(\sum _{r=1} {V}n_{(\cdot),r}^{i}+\beta _{r}\right)}}}\end{aligned}}}$

Finalmente, vamos ${\displaystyle n_{j,r}{i,-(m,n)}$ ser el mismo significado ${\displaystyle n_{j,r} {i}}$ pero con ${\displaystyle Z_{(m,n)}$ excluido. La ecuación anterior puede ser más simplificada aprovechando la propiedad de la función gamma. Primero dividimos la suma y luego la fusionamos para obtener una ${\displaystyle k}$-Summación independiente, que podría ser bajada:

${\displaystyle {\begin{aligned} limit\propto \prod _{i\neq k}\Gamma \left(n_{m,(\cdot)}}{i,-(m,n)}+\alpha _{i}\right)\prod _{i\neq k}{\frac {\fnMicrosoft Sans Serif}+\beta _{v}\right)}{\i,-(m,n)}\beta Gamma \left(\sum _{r=1}{V}n_{(\cdot),r}^{i,-(m,n)}+\beta _{r}\right)}\ Gamma \left(n_{m,(\cdot)}^{k,-(m,n)}+\alpha _{k}+1\right){\frac {\fnMicrosoft Sans Serif}\beta _{v}+1\right)}{\k,-(m,n)}+\beta Gamma \left(\sum _{V}n_{(\cdot),r}{k,-(m,n)}+\beta _{r}+1\right)}\[8pt] limit=\prod _{i\neq k}\Gamma\left(n_{m,(\cdot)}{i,-m\i {\fnMicrosoft Sans Serif}+\beta _{v}\right)}{\i,-(m,n)}\beta Gamma \left(\sum _{r=1}{V}n_{(\cdot),r}^{i,-(m,n)}+\beta _{r}\right)}\ Gamma \left(n_{m,(\cdot)}^{k,-(m,n)}+\alpha _{k}\right){\frac {\Gamma\left(n_{(\cdot),v}^{k,-(m,n)}+\beta _{v}\right)}{\c] Gamma \left(\sum _{V}n_{(\cdot),r}{k,-(m,n)}+\beta _{r}\right)}}\left(n_{m,(\cdot)}{k,-(m,n)}+\alpha _{k}{k}{k}{k} {n_p] ¿Por qué? {\fnMicrosoft Sans Serif}+\beta _{v}\right)}{\i,-(m,n)}\beta Gamma \left(\sum _{V}n_{(\cdot),r}{i,-(m,n)}+\beta _{r}\right)}}\left(n_{m,(\cdot)}{k,-(m,n)}+\alpha _{k}{k}{k}{k} {n_p] ¿Qué? ¿Por qué?$

Tenga en cuenta que la misma fórmula se deriva en el artículo sobre la distribución multinomial de Dirichlet, como parte de una discusión más general sobre la integración de valores a priori de la distribución de Dirichlet a partir de una red bayesiana.

El modelado de temas es una solución clásica al problema de la recuperación de información mediante el uso de datos vinculados y tecnología de la web semántica. Los modelos y técnicas relacionados son, entre otros, la indexación semántica latente, el análisis de componentes independientes, la indexación semántica latente probabilística, la factorización matricial no negativa y la distribución Gamma-Poisson.

El modelo LDA es altamente modular y, por lo tanto, se puede ampliar fácilmente. El principal campo de interés es el modelado de relaciones entre temas. Esto se logra utilizando otra distribución en el símplex en lugar de la de Dirichlet. El modelo de temas correlacionados sigue este enfoque, induciendo una estructura de correlación entre temas utilizando la distribución normal logística en lugar de la de Dirichlet. Otra extensión es el LDA jerárquico (hLDA), donde los temas se unen en una jerarquía utilizando el proceso de restaurante chino anidado, cuya estructura se aprende a partir de los datos. El LDA también se puede extender a un corpus en el que un documento incluye dos tipos de información (por ejemplo, palabras y nombres), como en el modelo LDA dual. Las extensiones no paramétricas del LDA incluyen el modelo de mezcla de procesos Dirichlet jerárquico, que permite que el número de temas sea ilimitado y se aprenda a partir de los datos.

Como se señaló anteriormente, el PLSA es similar al LDA. El modelo LDA es esencialmente la versión bayesiana del modelo pLSA. La formulación bayesiana tiende a funcionar mejor en pequeños conjuntos de datos porque los métodos Bayesianos pueden evitar la superposición de los datos. Para conjuntos de datos muy grandes, los resultados de los dos modelos tienden a converger. Una diferencia es que pLSA utiliza una variable ${\displaystyle d}$ para representar un documento en el conjunto de capacitación. Así que en pLSA, cuando se presenta con un documento que el modelo no ha visto antes, arreglamos ${\displaystyle \Pr(w\mid z)}$—la probabilidad de que las palabras bajo temas— sean las que aprendieron del conjunto de entrenamiento y usen el mismo algoritmo EM para inferir ${\displaystyle \Pr(z\mid d)}$- la distribución de temas bajo ${\displaystyle d}$. Blei argumenta que este paso es engañar porque usted está esencialmente reajustando el modelo a los nuevos datos.

En biología evolutiva, suele ser natural suponer que las ubicaciones geográficas de los individuos observados aportan cierta información sobre su ascendencia. Esta es la razón de ser de varios modelos para datos genéticos georreferenciados.

Se han utilizado variaciones de LDA para clasificar automáticamente imágenes naturales en categorías, como "dormitorio" o "bosque", tratando una imagen como un documento y pequeñas partes de la imagen como palabras; una de las variaciones se denomina asignación de Dirichlet latente espacial.

• Variational Bayesian methods
• Pachinko allocation
• tf-idf
• Infer.NET

• jLDADMM Un paquete Java para modelar temas en textos normales o cortos. jLDADMM incluye las implementaciones del modelo de tema LDA y el un tema por documento Dirichlet Multinomial Mixture model. jLDADMM también proporciona una implementación para la evaluación de agrupación de documentos para comparar modelos de temas.
• STTM A Java package for short text topic modeling (https://github.com/qiang2100/STTM). STPUTM incluye estos siguientes algoritmos: Dirichlet Multinomial Mixture (DMM) en la conferencia KDD2014, Biterm Topic Model (BTM) en la revista TKDE2016, Word Network Topic Model (WNTM) en la revista KAIS2018, Pseudo-Document-Based Topic Model (PTM) en la conferencia KDD2015 STTM también incluye seis corpus de texto corto para la evaluación. STTM presenta tres aspectos sobre cómo evaluar el rendimiento de los algoritmos (es decir, coherencia de temas, agrupación y clasificación).
• Conferencia que cubre algunas de las notaciones en este artículo: LDA y Modelado Tópico Video Conferencia de David Blei o misma conferencia en YouTube
• D. Bibliografía de LDA de Mimno Una lista exhaustiva de los recursos relacionados con el LDA (incl. documentos y algunas implementaciones)
• Gensim, un Python+NumPy aplicación de LDA en línea para entradas más grandes que la RAM disponible.
• tópicos y lda son dos paquetes R para el análisis de LDA.
• MALLET Paquete basado en Java de código abierto de la Universidad de Massachusetts-Amherst para modelar temas con LDA, también tiene un GUI desarrollado independientemente, la herramienta de modelado de tema
• LDA en Mahout implementación de LDA utilizando MapReduce en la plataforma Hadoop
• Latent Dirichlet Allocation (LDA) Tutorial for the Infer. Marco de computación de máquinas NET Microsoft Research C# Machine Learning Framework
• LDA en Spark: Desde la versión 1.3.0, Apache Spark también cuenta con una implementación de LDA
• LDA, exampleLDA Aplicación del MATLAB