Ascensor (fuerza)

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Fuerza perpendicular al flujo de líquido circundante

El 1902 Wright Glider muestra su elevación al levantarse

Un fluido que fluye alrededor de un objeto ejerce una fuerza sobre él. Elevación es el componente de esta fuerza que es perpendicular a la dirección del flujo que se aproxima. Contrasta con la fuerza de arrastre, que es la componente de la fuerza paralela a la dirección del flujo. El ascensor actúa convencionalmente en dirección ascendente para contrarrestar la fuerza de la gravedad, pero puede actuar en cualquier dirección en ángulo recto con el flujo.

Si el fluido circundante es aire, la fuerza se denomina fuerza aerodinámica. En agua o cualquier otro líquido, se llama fuerza hidrodinámica.

La elevación dinámica se distingue de otros tipos de elevación en fluidos. Ascensor aerostático o flotabilidad, en el que un fluido interno es más liviano que el fluido circundante, no requiere movimiento y es utilizado por globos, dirigibles, dirigibles, botes y submarinos. El ascensor de planeo, en el que solo la parte inferior del cuerpo se sumerge en un flujo de líquido, es utilizado por lanchas a motor, tablas de surf, windsurf, veleros y esquís acuáticos.

Resumen

El elevador se define como el componente de la fuerza aerodinámica perpendicular a la dirección de flujo, y el arrastrar es el componente que es paralelo a la dirección de flujo.

Un fluido que fluye alrededor de la superficie de un objeto sólido aplica una fuerza sobre él. No importa si el objeto se mueve a través de un fluido estacionario (p. ej., un avión que vuela por el aire) o si el objeto está estacionario y el fluido se mueve (p. ej., un ala en un túnel de viento) o si ambos se mueven (p. ej., un velero usando el viento para avanzar). Elevación es el componente de esta fuerza que es perpendicular a la dirección del flujo que se aproxima. La sustentación siempre va acompañada de una fuerza de arrastre, que es la componente de la fuerza superficial paralela a la dirección del flujo.

La sustentación se asocia principalmente con las alas de los aviones de ala fija, aunque es generada más ampliamente por muchos otros cuerpos aerodinámicos, como hélices, cometas, rotores de helicópteros, alas de autos de carrera, velas marítimas, turbinas eólicas y quillas de veleros., timones de barcos e hidroalas en el agua. La sustentación también es utilizada por animales voladores y deslizantes, especialmente por pájaros, murciélagos e insectos, e incluso en el mundo vegetal por las semillas de ciertos árboles. Mientras que el significado común de la palabra "ascensor" asume que la sustentación se opone al peso, la sustentación puede estar en cualquier dirección con respecto a la gravedad, ya que se define con respecto a la dirección del flujo en lugar de la dirección de la gravedad. Cuando un avión navega en vuelo recto y nivelado, la mayor parte de la sustentación se opone a la gravedad. Sin embargo, cuando una aeronave está ascendiendo, descendiendo o ladeándose en un viraje, la sustentación se inclina con respecto a la vertical. La sustentación también puede actuar como carga aerodinámica en algunas maniobras acrobáticas o en el ala de un automóvil de carreras. La sustentación también puede ser en gran parte horizontal, por ejemplo, en un velero.

La sustentación que se analiza en este artículo se relaciona principalmente con los perfiles aerodinámicos, aunque los hidroalas marinas y las hélices comparten los mismos principios físicos y funcionan de la misma manera, a pesar de las diferencias entre el aire y el agua, como la densidad, la compresibilidad y la viscosidad.

El flujo alrededor de un perfil aerodinámico que se eleva es un fenómeno de mecánica de fluidos que se puede entender esencialmente en dos niveles: existen teorías matemáticas, que se basan en leyes establecidas de la física y representan el flujo con precisión, pero que requieren resolver ecuaciones diferenciales parciales. Y hay explicaciones físicas sin matemáticas, que son menos rigurosas. Es difícil explicar correctamente la sustentación en estos términos cualitativos porque las relaciones de causa y efecto involucradas son sutiles. Una explicación completa que capte todos los aspectos esenciales es necesariamente compleja. También hay muchas explicaciones simplificadas, pero todas dejan partes significativas del fenómeno sin explicar, mientras que algunas también tienen elementos que son simplemente incorrectos.

Explicaciones físicas simplificadas de sustentación en un perfil aerodinámico

Una sección cruzada de un ala define una forma de aire.

Un perfil aerodinámico es una forma aerodinámica que es capaz de generar significativamente más sustentación que resistencia. Una placa plana puede generar sustentación, pero no tanto como un perfil aerodinámico aerodinámico, y con un arrastre algo mayor. La mayoría de las explicaciones simplificadas siguen uno de los dos enfoques básicos, basados en las leyes del movimiento de Newton o en el principio de Bernoulli.

Explicación basada en la desviación del flujo y las leyes de Newton

Cuando un avión genera elevación, desvía el aire hacia abajo, y para hacerlo debe ejercer una fuerza descendente en el aire. La tercera ley de Newton requiere que el aire debe ejercer una fuerza ascendente igual en el aire.

Un perfil aerodinámico genera sustentación ejerciendo una fuerza hacia abajo sobre el aire a medida que pasa. De acuerdo con la tercera ley de Newton, el aire debe ejercer una fuerza igual y opuesta (hacia arriba) sobre la superficie aerodinámica, que es la sustentación.

A medida que el flujo de aire se acerca al perfil aerodinámico, se curva hacia arriba, pero cuando pasa por el perfil aerodinámico, cambia de dirección y sigue un camino que se curva hacia abajo. De acuerdo con la segunda ley de Newton, este cambio en la dirección del flujo requiere una fuerza hacia abajo aplicada al aire por el perfil aerodinámico. Entonces, la tercera ley de Newton requiere que el aire ejerza una fuerza ascendente sobre el perfil aerodinámico; por lo tanto, se genera una fuerza de reacción, sustentación, opuesta al cambio de dirección. En el caso del ala de un avión, el ala ejerce una fuerza hacia abajo sobre el aire y el aire ejerce una fuerza hacia arriba sobre el ala.

El giro hacia abajo del flujo no se produce únicamente por la superficie inferior del perfil aerodinámico, y el flujo de aire por encima del perfil aerodinámico representa gran parte de la acción de giro hacia abajo.

Esta explicación es correcta pero está incompleta. No explica cómo el perfil aerodinámico puede impartir un giro hacia abajo a una franja mucho más profunda del flujo de lo que realmente toca. Además, no menciona que la fuerza de elevación se ejerce por diferencias de presión y no explica cómo se mantienen esas diferencias de presión.

Controversia sobre el efecto Coandă

Algunas versiones de la explicación de la sustentación por desviación del flujo citan el efecto Coandă como la razón por la cual el flujo puede seguir la superficie superior convexa del perfil aerodinámico. La definición convencional en el campo de la aerodinámica es que el efecto Coandă se refiere a la tendencia de un chorro de fluido a permanecer adherido a una superficie adyacente que se curva alejándose del flujo, y el arrastre resultante de aire ambiental en el flujo.

En términos más generales, algunos consideran que el efecto incluye la tendencia de cualquier capa límite de fluido a adherirse a una superficie curva, no solo la capa límite que acompaña a un chorro de fluido. Es en este sentido más amplio que algunas referencias populares utilizan el efecto Coandă para explicar por qué el flujo de aire permanece adherido a la parte superior de un perfil aerodinámico. Este es un uso controvertido del término "efecto Coandă"; el flujo que sigue a la superficie superior simplemente refleja la ausencia de separación de la capa límite, por lo que no es un ejemplo del efecto Coandă. Independientemente de si esta definición más amplia del "efecto Coandă" es aplicable, llamándolo el "efecto Coandă" no proporciona una explicación, solo le da un nombre al fenómeno.

La capacidad del flujo de un fluido para seguir una trayectoria curva no depende de las fuerzas de corte, la viscosidad del fluido o la presencia de una capa límite. El aire que fluye alrededor de un perfil aerodinámico, se adhiere a las superficies superior e inferior y genera sustentación, se acepta como un fenómeno en el flujo no viscoso.

Explicaciones basadas en un aumento de la velocidad del flujo y el principio de Bernoulli

Hay dos versiones comunes de esta explicación, una basada en "igual tiempo de tránsito" y otra basada en "obstrucción" del flujo de aire.

Una ilustración de la explicación incorrecta de tiempo de tránsito igual de la elevación de aire.

Explicación falsa basada en el mismo tiempo de tránsito

El "tiempo de tránsito igual" La explicación comienza argumentando que el flujo sobre la superficie superior es más rápido que el flujo sobre la superficie inferior porque la longitud de la trayectoria sobre la superficie superior es más larga y debe atravesarse en el mismo tiempo de tránsito. El principio de Bernoulli establece que, bajo ciertas condiciones, una mayor velocidad de flujo se asocia con una presión reducida. Se concluye que la presión reducida sobre la superficie superior da como resultado una elevación hacia arriba.

Un defecto grave en la explicación del tiempo de tránsito igual es que no explica correctamente qué hace que el flujo se acelere. La explicación de la longitud de ruta más larga es simplemente incorrecta. No se necesita ninguna diferencia en la longitud de la trayectoria, e incluso cuando hay una diferencia, normalmente es demasiado pequeña para explicar la diferencia de velocidad observada. Esto se debe a que la suposición de un tiempo de tránsito igual es incorrecta. No existe un principio físico que requiera el mismo tiempo de tránsito y los resultados experimentales muestran que esta suposición es falsa. De hecho, el aire que se mueve sobre la parte superior de un perfil aerodinámico que genera sustentación se mueve mucho más rápido de lo que predice la teoría del tránsito uniforme. La velocidad de flujo mucho más alta sobre la superficie superior se puede ver claramente en esta visualización de flujo animado.

Obstrucción del flujo de aire

Streamlines y streamtubes alrededor de un ascensor generador de airefoil. Observe las secuencias más estrechas de arriba y las secuencias más anchas de abajo.

Al igual que la explicación del tiempo de tránsito igual, la "obstrucción" o "pinzamiento del tubo de corriente" La explicación argumenta que el flujo sobre la superficie superior es más rápido que el flujo sobre la superficie inferior, pero da una razón diferente para la diferencia de velocidad. Argumenta que la superficie superior curva actúa más como un obstáculo para el flujo, lo que obliga a las líneas de corriente a apretarse más, haciendo que los tubos de corriente sean más estrechos. Cuando los tubos de corriente se vuelven más estrechos, la conservación de la masa requiere que aumente la velocidad del flujo. La presión reducida en la superficie superior y la sustentación hacia arriba se derivan de la velocidad más alta por el principio de Bernoulli, al igual que en la explicación del tiempo de tránsito igual. A veces se hace una analogía con una boquilla venturi, alegando que la superficie superior del ala actúa como una boquilla venturi para restringir el flujo.

Un defecto grave en la explicación de la obstrucción es que no explica cómo se produce el pinzamiento del tubo de corriente o por qué es mayor en la superficie superior que en la superficie inferior. Para alas convencionales que son planas en la parte inferior y curvadas en la parte superior, esto tiene cierto sentido intuitivo, pero no explica cómo las placas planas, los perfiles aerodinámicos simétricos, las velas de los veleros o los perfiles aerodinámicos convencionales que vuelan al revés pueden generar sustentación, y los intentos de calcular la sustentación se basan en en la cantidad de constricción u obstrucción no predicen los resultados experimentales. Otro defecto es que la conservación de la masa no es una razón física satisfactoria por la que el flujo se aceleraría. Explicar realmente por qué algo se acelera requiere identificar la fuerza que lo hace acelerar.

Problemas comunes a ambas versiones de la explicación basada en Bernoulli

Un defecto grave común a todas las explicaciones basadas en Bernoulli es que implican que una diferencia de velocidad puede surgir de causas distintas a la diferencia de presión, y que la diferencia de velocidad conduce a una diferencia de presión, según el principio de Bernoulli. Esta causalidad unidireccional implícita es un concepto erróneo. La relación real entre la presión y la velocidad del flujo es una interacción mutua. Como se explica a continuación en una explicación física más completa, producir una fuerza de sustentación requiere mantener las diferencias de presión tanto en la dirección vertical como en la horizontal. Las explicaciones de solo Bernoulli no explican cómo se mantienen las diferencias de presión en la dirección vertical. Es decir, dejan fuera la parte de flujo-desviación de la interacción.

Aunque las dos explicaciones simples basadas en Bernoulli anteriores son incorrectas, no hay nada incorrecto sobre el principio de Bernoulli o el hecho de que el aire va más rápido en la parte superior del ala, y el principio de Bernoulli puede ser utilizado correctamente como parte de una explicación más complicada de elevación.

Atributos básicos del ascensor

La sustentación es el resultado de las diferencias de presión y depende del ángulo de ataque, la forma del perfil aerodinámico, la densidad del aire y la velocidad del aire.

Diferencias de presión

La presión es la fuerza normal por unidad de área que ejerce el aire sobre sí mismo y sobre las superficies que toca. La fuerza de sustentación se transmite a través de la presión, que actúa perpendicularmente a la superficie del perfil aerodinámico. Así, la fuerza neta se manifiesta como diferencias de presión. La dirección de la fuerza neta implica que la presión promedio en la superficie superior del perfil aerodinámico es menor que la presión promedio en la parte inferior.

Estas diferencias de presión surgen junto con el flujo de aire curvo. Cuando un fluido sigue una trayectoria curva, hay un gradiente de presión perpendicular a la dirección del flujo con una presión más alta en el exterior de la curva y una presión más baja en el interior. Esta relación directa entre las líneas de corriente curvas y las diferencias de presión, a veces denominada teorema de la curvatura de la línea de corriente, se derivó de la segunda ley de Newton por Leonhard Euler en 1754:

frac{operatorname{d}p}{operatorname{d}R}= rho frac{v^2}{R}

El lado izquierdo de esta ecuación representa la diferencia de presión perpendicular al flujo de fluido. En el lado derecho, ρ es la densidad, v es la velocidad y R es el radio de curvatura. Esta fórmula muestra que velocidades más altas y curvaturas más estrechas crean diferenciales de presión más grandes y que para flujo directo (R → ∞) la diferencia de presión es cero.

Ángulo de ataque

Ángulo de ataque de un avión

El ángulo de ataque es el ángulo entre la línea de cuerda de un perfil aerodinámico y el flujo de aire que se aproxima. Un perfil aerodinámico simétrico generará una sustentación cero con un ángulo de ataque cero. Pero a medida que aumenta el ángulo de ataque, el aire se desvía en un ángulo mayor y la componente vertical de la velocidad de la corriente de aire aumenta, lo que da como resultado una mayor sustentación. Para ángulos pequeños, una superficie aerodinámica simétrica generará una fuerza de sustentación aproximadamente proporcional al ángulo de ataque.

A medida que aumenta el ángulo de ataque, la sustentación alcanza un máximo en algún ángulo; aumentar el ángulo de ataque más allá de este ángulo de ataque crítico hace que el flujo de la superficie superior se separe del ala; hay menos desviación hacia abajo, por lo que el perfil aerodinámico genera menos sustentación. Se dice que el perfil aerodinámico está estancado.

Forma aerodinámica

Una lámina de aire con camber en comparación con una lámina de aire simétrica

La fuerza de sustentación máxima que puede generar un perfil aerodinámico a una velocidad aerodinámica determinada depende de la forma del perfil aerodinámico, especialmente de la cantidad de inclinación (curvatura tal que la superficie superior es más convexa que la superficie inferior, como se ilustra a la derecha). El aumento de la inclinación generalmente aumenta la sustentación máxima a una velocidad determinada.

Las superficies aerodinámicas combadas generarán sustentación con un ángulo de ataque cero. Cuando la línea de la cuerda es horizontal, el borde de fuga tiene una dirección hacia abajo y dado que el aire sigue al borde de fuga, se desvía hacia abajo. Cuando un perfil aerodinámico combado está boca abajo, el ángulo de ataque se puede ajustar para que la fuerza de sustentación sea hacia arriba. Esto explica cómo un avión puede volar boca abajo.

Condiciones de flujo

Las condiciones de flujo ambiental que afectan la sustentación incluyen la densidad del fluido, la viscosidad y la velocidad del flujo. La densidad se ve afectada por la temperatura y por la velocidad acústica del medio, es decir, por los efectos de compresibilidad.

Velocidad y densidad del aire

La elevación es proporcional a la densidad del aire y aproximadamente proporcional al cuadrado de la velocidad del flujo. La sustentación también depende del tamaño del ala, siendo generalmente proporcional al área del ala proyectada en la dirección de sustentación. En los cálculos, es conveniente cuantificar la sustentación en términos de un coeficiente de sustentación basado en estos factores.

Capa límite y arrastre de perfil

No importa cuán suave parezca la superficie de un perfil aerodinámico, cualquier superficie es áspera en la escala de las moléculas de aire. Las moléculas de aire que vuelan hacia la superficie rebotan en la superficie rugosa en direcciones aleatorias en relación con sus velocidades originales. El resultado es que cuando el aire se ve como un material continuo, se ve que no puede deslizarse a lo largo de la superficie, y la velocidad del aire en relación con el perfil aerodinámico disminuye a casi cero en la superficie (es decir, el aire las moléculas se 'pegan' a la superficie en lugar de deslizarse a lo largo de ella), lo que se conoce como la condición de no deslizamiento. Debido a que el aire en la superficie tiene una velocidad cercana a cero pero el aire que se aleja de la superficie se está moviendo, existe una delgada capa límite en la que el aire cercano a la superficie está sujeto a un movimiento de cizallamiento. La viscosidad del aire resiste el cizallamiento, lo que da lugar a un esfuerzo de cizallamiento en la superficie del perfil aerodinámico denominado arrastre por fricción superficial. En la mayor parte de la superficie de la mayoría de los perfiles aerodinámicos, la capa límite es naturalmente turbulenta, lo que aumenta la fricción superficial.

En condiciones de vuelo normales, la capa límite permanece adherida a las superficies superior e inferior hasta el borde de salida y su efecto en el resto del flujo es modesto. En comparación con las predicciones de la teoría del flujo no viscoso, en la que no hay una capa límite, la capa límite adjunta reduce la sustentación en una cantidad modesta y modifica un poco la distribución de la presión, lo que da como resultado un arrastre de presión relacionado con la viscosidad por encima de la fricción superficial. arrastrar. El total del arrastre por fricción superficial y el arrastre por presión relacionado con la viscosidad generalmente se denomina arrastre de perfil.

Estancamiento

Flujo de aire que se separa de un ala en un ángulo alto de ataque

La elevación máxima de un perfil aerodinámico a una velocidad determinada está limitada por la separación de la capa límite. A medida que aumenta el ángulo de ataque, se llega a un punto en el que la capa límite ya no puede permanecer unida a la superficie superior. Cuando la capa límite se separa, deja una región de flujo recirculante sobre la superficie superior, como se ilustra en la fotografía de visualización de flujo a la derecha. Esto se conoce como stall, o stalling. En ángulos de ataque por encima de la pérdida, la sustentación se reduce significativamente, aunque no llega a cero. La sustentación máxima que se puede lograr antes de entrar en pérdida, en términos del coeficiente de sustentación, es generalmente inferior a 1,5 para superficies aerodinámicas de un solo elemento y puede ser superior a 3,0 para superficies aerodinámicas con flaps ranurados de alta sustentación y dispositivos de borde de ataque desplegados.

Cuerpos de farol

El flujo alrededor de cuerpos rocosos, es decir, sin una forma aerodinámica o superficies aerodinámicas estancadas, también puede generar sustentación, además de una fuerte fuerza de arrastre. Esta elevación puede ser constante o puede oscilar debido al desprendimiento de vórtices. La interacción de la flexibilidad del objeto con el desprendimiento del vórtice puede mejorar los efectos de la elevación fluctuante y causar vibraciones inducidas por el vórtice. Por ejemplo, el flujo alrededor de un cilindro circular genera una calle de vórtices de Kármán: los vórtices se desprenden de forma alterna desde los lados del cilindro. La naturaleza oscilatoria del flujo produce una fuerza de sustentación fluctuante en el cilindro, aunque la fuerza neta (media) es insignificante. La frecuencia de la fuerza de sustentación se caracteriza por el número de Strouhal adimensional, que depende del número de Reynolds del flujo.

Para una estructura flexible, esta fuerza de elevación oscilatoria puede inducir vibraciones inducidas por vórtices. Bajo ciertas condiciones, por ejemplo, resonancia o fuerte correlación transversal de la fuerza de sustentación, el movimiento resultante de la estructura debido a las fluctuaciones de sustentación puede mejorar considerablemente. Tales vibraciones pueden plantear problemas y amenazar con colapsar estructuras altas hechas por el hombre como chimeneas industriales.

En el efecto Magnus, un cilindro que gira en una corriente libre genera una fuerza de sustentación. Aquí la rotación mecánica actúa sobre la capa límite, haciendo que se separe en diferentes lugares en los dos lados del cilindro. La separación asimétrica cambia la forma efectiva del cilindro en lo que respecta al flujo, de modo que el cilindro actúa como un perfil aerodinámico de elevación con circulación en el flujo exterior.

Una explicación física más completa

Como se describió anteriormente en "Explicaciones físicas simplificadas de sustentación en un perfil aerodinámico", hay dos explicaciones populares principales: una basada en la desviación hacia abajo del flujo (leyes de Newton) y otra basada sobre diferencias de presión acompañadas de cambios en la velocidad del flujo (principio de Bernoulli). Cualquiera de estos, por sí solo, identifica correctamente algunos aspectos del flujo de elevación, pero deja sin explicar otros aspectos importantes del fenómeno. Una explicación más completa involucra tanto la desviación hacia abajo como las diferencias de presión (incluidos los cambios en la velocidad del flujo asociados con las diferencias de presión), y requiere observar el flujo con más detalle.

Elevación en la superficie aerodinámica

La forma aerodinámica y el ángulo de ataque trabajan juntos para que la superficie aerodinámica ejerza una fuerza descendente sobre el aire a medida que pasa. De acuerdo con la tercera ley de Newton, el aire debe ejercer una fuerza igual y opuesta (hacia arriba) sobre la superficie aerodinámica, que es la sustentación.

La fuerza neta ejercida por el aire se produce como una diferencia de presión sobre las superficies aerodinámicas. La presión en un fluido siempre es positiva en un sentido absoluto, por lo que siempre debe pensarse que la presión empuja y nunca tira. Por lo tanto, la presión empuja hacia adentro el perfil aerodinámico en todas partes, tanto en la superficie superior como en la inferior. El aire que fluye reacciona a la presencia del ala reduciendo la presión en la superficie superior del ala y aumentando la presión en la superficie inferior. La presión sobre la superficie inferior empuja hacia arriba con más fuerza que la presión reducida sobre la superficie superior empuja hacia abajo, y el resultado neto es una elevación hacia arriba.

La diferencia de presión que produce la sustentación actúa directamente sobre las superficies aerodinámicas; sin embargo, comprender cómo se produce la diferencia de presión requiere comprender qué hace el flujo en un área más amplia.

El flujo más amplio alrededor del perfil aerodinámico

Flujo alrededor de una lámina de aire: los puntos se mueven con el flujo. Los puntos negros son rebanados a tiempo, que se dividen en dos – una parte superior e inferior – en el borde principal. Una marcada diferencia de velocidad entre las aerolíneas de superficie superior e inferior se muestra más claramente en la animación de la imagen, con los marcadores superiores que llegan al borde de seguimiento mucho antes de las inferiores. Los colores de los puntos indican aerosoles.

Un perfil aerodinámico afecta la velocidad y la dirección del flujo en un área amplia, produciendo un patrón llamado campo de velocidad. Cuando un perfil aerodinámico produce sustentación, el flujo por delante del perfil aerodinámico se desvía hacia arriba, el flujo por encima y por debajo del perfil aerodinámico se desvía hacia abajo, y el flujo detrás del perfil aerodinámico se desvía hacia arriba nuevamente, dejando el aire muy por detrás del perfil aerodinámico en el mismo estado que el flujo que se aproxima muy por delante. El flujo por encima de la superficie superior se acelera, mientras que el flujo por debajo del perfil aerodinámico se ralentiza. Junto con la desviación hacia arriba del aire en el frente y la desviación hacia abajo del aire inmediatamente detrás, esto establece un componente circulatorio neto del flujo. La desviación hacia abajo y los cambios en la velocidad del flujo son pronunciados y se extienden sobre un área amplia, como se puede ver en la animación del flujo a la derecha. Estas diferencias en la dirección y la velocidad del flujo son mayores cerca del perfil aerodinámico y disminuyen gradualmente muy por encima y por debajo. Todas estas características del campo de velocidad también aparecen en modelos teóricos para flujos de elevación.

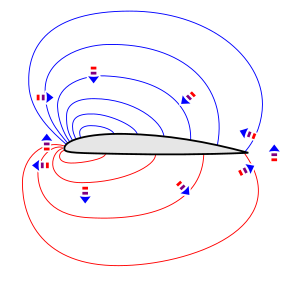
La presión también se ve afectada en un área amplia, en un patrón de presión no uniforme llamado campo de presión. Cuando un perfil aerodinámico produce sustentación, hay una región difusa de baja presión sobre el perfil aerodinámico y, por lo general, una región difusa de alta presión debajo, como se ilustra en las isobaras (curvas de presión constante) en el dibujo. La diferencia de presión que actúa sobre la superficie es solo una parte de este campo de presión.

Interacción mutua de diferencias de presión y cambios en la velocidad del flujo

Campo de presión alrededor de un avión. Las líneas son isobars de igual presión a lo largo de su longitud. Las flechas muestran el diferencial de presión de alto (rojo) a bajo (azul) y por lo tanto también la fuerza neta que hace que el aire se acelere en esa dirección.

La presión no uniforme ejerce fuerzas sobre el aire en la dirección de mayor a menor presión. La dirección de la fuerza es diferente en diferentes lugares alrededor de la superficie aerodinámica, como lo indican las flechas de bloque en la figura campo de presión alrededor de una superficie aerodinámica. El aire por encima del perfil aerodinámico es empujado hacia el centro de la región de baja presión, y el aire por debajo del perfil aerodinámico es empujado hacia afuera desde el centro de la región de alta presión.

Según la segunda ley de Newton, una fuerza hace que el aire se acelere en la dirección de la fuerza. Por lo tanto, las flechas verticales en el diagrama de campo de presión adjunto indican que el aire por encima y por debajo de la superficie aerodinámica se acelera o gira hacia abajo, y que la presión no uniforme es, por lo tanto, la causa de la desviación hacia abajo del flujo visible en la animación de flujo. Para producir este giro hacia abajo, el perfil aerodinámico debe tener un ángulo de ataque positivo o tener suficiente inclinación positiva. Tenga en cuenta que el giro hacia abajo del flujo sobre la superficie superior es el resultado de que el aire es empujado hacia abajo por una presión más alta por encima que por debajo. Algunas explicaciones que se refieren al "efecto Coandă" sugieren que la viscosidad juega un papel clave en el giro hacia abajo, pero esto es falso. (ver arriba en "Controversia sobre el efecto Coandă").

Las flechas delante del perfil aerodinámico indican que el flujo delante del perfil aerodinámico se desvía hacia arriba, y las flechas detrás del perfil aerodinámico indican que el flujo detrás se desvía hacia arriba nuevamente, después de ser desviado hacia abajo sobre el perfil aerodinámico. Estas desviaciones también son visibles en la animación de flujo.

Las flechas por delante y por detrás del perfil aerodinámico también indican que el aire que pasa a través de la región de baja presión por encima del perfil aerodinámico se acelera al entrar y se vuelve más lento al salir. El aire que pasa a través de la región de alta presión debajo de la superficie aerodinámica se ralentiza cuando entra y luego vuelve a acelerar cuando sale. Por lo tanto, la presión no uniforme también es la causa de los cambios en la velocidad del flujo visibles en la animación del flujo. Los cambios en la velocidad del flujo son consistentes con el principio de Bernoulli, que establece que en un flujo constante sin viscosidad, una presión más baja significa una velocidad más alta y una presión más alta significa una velocidad más baja.

Por lo tanto, los cambios en la dirección y la velocidad del flujo se deben directamente a la presión no uniforme. Pero esta relación de causa y efecto no es solo unidireccional; trabaja en ambas direcciones simultáneamente. El movimiento del aire se ve afectado por las diferencias de presión, pero la existencia de las diferencias de presión depende del movimiento del aire. La relación es, por lo tanto, una interacción mutua o recíproca: el flujo de aire cambia de velocidad o dirección en respuesta a las diferencias de presión, y las diferencias de presión son sostenidas por la resistencia del aire al cambio de velocidad o dirección. Una diferencia de presión puede existir solo si hay algo contra lo que empujar. En el flujo aerodinámico, la diferencia de presión empuja contra la inercia del aire, ya que la diferencia de presión acelera el aire. Esta es la razón por la que la masa del aire es parte del cálculo y por la que la sustentación depende de la densidad del aire.

Mantener la diferencia de presión que ejerce la fuerza de sustentación sobre las superficies aerodinámicas requiere mantener un patrón de presión no uniforme en un área amplia alrededor del perfil aerodinámico. Esto requiere mantener las diferencias de presión tanto en la dirección vertical como en la horizontal y, por lo tanto, requiere un giro del flujo hacia abajo y cambios en la velocidad del flujo de acuerdo con el principio de Bernoulli. Las diferencias de presión y los cambios en la dirección y velocidad del flujo se sostienen mutuamente en una interacción mutua. Las diferencias de presión se derivan naturalmente de la segunda ley de Newton y del hecho de que el flujo a lo largo de la superficie sigue los contornos predominantemente inclinados hacia abajo del perfil aerodinámico. Y el hecho de que el aire tenga masa es crucial para la interacción.

Cómo las explicaciones más simples se quedan cortas

Producir una fuerza de sustentación requiere un giro del flujo hacia abajo y cambios en la velocidad del flujo de acuerdo con el principio de Bernoulli. Cada una de las explicaciones simplificadas dadas anteriormente en Explicaciones físicas simplificadas de la sustentación en un perfil aerodinámico se quedan cortas al tratar de explicar la sustentación en términos de solo una u otra, explicando así solo una parte del fenómeno y dejando otras partes sin explicar.

Ascenso de cuantificación

Integración de presión

Cuando se conoce la distribución de presión en la superficie aerodinámica, determinar la sustentación total requiere sumar las contribuciones a la fuerza de presión de los elementos locales de la superficie, cada uno con su propio valor local de presión. La sustentación total es, por lo tanto, la integral de la presión, en la dirección perpendicular al flujo de campo lejano, sobre la superficie aerodinámica.

{displaystyle L=oint pmathbf {n} cdot mathbf {k} ;mathrm {d} S,}

donde:

S es el área proyectada (planforme) del aeroplano, medido normal al flujo de aire medio;
n es el vector de unidad normal apuntando al ala;
k es el vector de unidad vertical, normal a la dirección freestream.

La ecuación de elevación anterior ignora las fuerzas de fricción de la piel, que son pequeñas en comparación con las fuerzas de presión.

Usando el vector a lo largo de la corriente i paralelo a la corriente libre en lugar de k en la integral, obtenemos una expresión para el arrastre de presión D_p (que incluye la porción de presión del perfil de arrastre y, si el ala es tridimensional, el arrastre inducido). Si usamos el vector longitudinal j, obtenemos la fuerza lateral Y.

{displaystyle {begin{aligned}D_{p}&=oint pmathbf {n} cdot mathbf {i} ;mathrm {d} S,\Y&=oint pmathbf {n} cdot mathbf {j} ;mathrm {d} S.end{aligned}}}

La validez de esta integración generalmente requiere que la forma del perfil aerodinámico sea una curva cerrada que sea suave por tramos.

Coeficiente de sustentación

El elevador depende del tamaño del ala, siendo aproximadamente proporcional al área del ala. A menudo es conveniente cuantificar el levantamiento de un avión dado por su coeficiente de elevación $C_{L}$ , que define su elevación general en términos de una zona unitaria del ala.

Si el valor de $C_{L}$ para un ala en un ángulo específico de ataque se da, entonces el ascensor producido para condiciones de flujo específicas se puede determinar:

L={tfrac 12}rho v^{2}SC_{L}

dónde

$L$ es la fuerza de elevación
$rho$ es la densidad del aire
$v$ es la velocidad o la verdadera velocidad del aire
$S$ es el área de ala planforme (proyectado)
$C_{L}$ es el coeficiente de elevación en el ángulo deseado de ataque, número Mach y número Reynolds

Teorías matemáticas del ascensor

Las teorías matemáticas de sustentación se basan en la mecánica de fluidos continuos, asumiendo que el aire fluye como un fluido continuo. La sustentación se genera de acuerdo con los principios fundamentales de la física, siendo los más relevantes los siguientes tres principios:

Conservación del impulso, que es consecuencia de las leyes de movimiento de Newton, especialmente la segunda ley de Newton que relaciona la fuerza neta en un elemento de aire a su tasa de cambio de impulso,
Conservación de la masa, incluyendo la suposición de que la superficie de la férula es impermeable para el aire que fluye alrededor, y
Conservación de la energía, que dice que la energía no es creada ni destruida.

Debido a que un perfil aerodinámico afecta el flujo en un área amplia a su alrededor, las leyes de conservación de la mecánica se incorporan en forma de ecuaciones diferenciales parciales combinadas con un conjunto de requisitos de condiciones de contorno que el flujo debe satisfacer en la superficie del perfil aerodinámico y lejos lejos del perfil aerodinámico.

Para predecir la sustentación se requiere resolver las ecuaciones para una forma de perfil aerodinámico y una condición de flujo en particular, lo que generalmente requiere cálculos que son tan voluminosos que solo son prácticos en una computadora, a través de métodos de dinámica de fluidos computacional (CFD). Determinar la fuerza aerodinámica neta de una solución CFD requiere "sumar" (integrando) las fuerzas debidas a la presión y al corte determinadas por el CFD sobre cada elemento de la superficie del perfil aerodinámico como se describe en "integración de presión".

Las ecuaciones de Navier-Stokes (NS) proporcionan la teoría de sustentación potencialmente más precisa, pero en la práctica, capturar los efectos de la turbulencia en la capa límite en la superficie aerodinámica requiere sacrificar cierta precisión y requiere el uso del promedio de Reynolds. Ecuaciones de Navier-Stokes (RANS). También se han desarrollado teorías más simples pero menos precisas.

Ecuaciones de Navier-Stokes (NS)

Estas ecuaciones representan la conservación de la masa, la segunda ley de Newton (conservación del impulso), la conservación de la energía, la ley de Newton para la acción de la viscosidad, la ley de conducción de calor de Fourier, una ecuación de estado que relaciona la densidad, la temperatura y presión, y fórmulas para la viscosidad y la conductividad térmica del fluido.

En principio, las ecuaciones NS, combinadas con las condiciones de contorno de ausencia de flujo continuo y ausencia de deslizamiento en la superficie aerodinámica, podrían utilizarse para predecir la sustentación en cualquier situación en un vuelo atmosférico normal con gran precisión. Sin embargo, los flujos de aire en situaciones prácticas siempre implican turbulencia en la capa límite junto a la superficie del perfil aerodinámico, al menos sobre la parte trasera del perfil aerodinámico. Predecir la sustentación resolviendo las ecuaciones NS en su forma original requeriría los cálculos para resolver los detalles de la turbulencia, hasta el remolino más pequeño. Esto todavía no es posible, ni siquiera en el ordenador actual más potente. Entonces, en principio, las ecuaciones NS proporcionan una teoría completa y muy precisa de la sustentación, pero la predicción práctica de la sustentación requiere que los efectos de la turbulencia se modelen en las ecuaciones RANS en lugar de calcularse directamente.

Ecuaciones de Navier-Stokes (RANS) promediadas por Reynolds

Estas son las ecuaciones NS con los movimientos de turbulencia promediados en el tiempo y los efectos de la turbulencia en el flujo promediado en el tiempo representado por el modelo de turbulencia (un conjunto adicional de ecuaciones basado en una combinación de análisis dimensional e información empírica sobre cómo la turbulencia afecta una capa límite en un sentido promedio promediado en el tiempo). Una solución RANS consiste en el vector de velocidad promediado en el tiempo, la presión, la densidad y la temperatura definidos en una cuadrícula densa de puntos que rodean la superficie aerodinámica.

La cantidad de cómputo requerida es una fracción minúscula (mil millonésimas) de lo que se requeriría para resolver todos los movimientos de turbulencia en un cálculo NS sin procesar, y con computadoras grandes disponibles, ahora es práctico realizar cálculos RANS para aviones completos. en tres dimensiones. Debido a que los modelos de turbulencia no son perfectos, la precisión de los cálculos RANS es imperfecta, pero es adecuada para el diseño práctico de aeronaves. La elevación pronosticada por RANS generalmente está dentro de un pequeño porcentaje de la elevación real.

Ecuaciones de flujo no viscoso (Euler o potencial)

Las ecuaciones de Euler son las ecuaciones de NS sin los efectos de viscosidad, conducción de calor y turbulencia. Al igual que con una solución RANS, una solución de Euler consiste en el vector de velocidad, la presión, la densidad y la temperatura definidos en una cuadrícula densa de puntos que rodean la superficie aerodinámica. Si bien las ecuaciones de Euler son más simples que las ecuaciones de NS, no se prestan a soluciones analíticas exactas.

Se puede simplificar aún más a través de la teoría del flujo potencial, que reduce el número de incógnitas a determinar y hace posibles las soluciones analíticas en algunos casos, como se describe a continuación.

Cálculos de Euler o de flujo potencial predicen la distribución de la presión en las superficies aerodinámicas aproximadamente correctamente para los ángulos de ataque por debajo de la pérdida, donde podrían perder la sustentación total hasta en un 10-20 %. En ángulos de ataque por encima de la entrada en pérdida, los cálculos no viscosos no predicen que se haya producido la entrada en pérdida y, como resultado, sobreestiman enormemente la sustentación.

En la teoría del flujo potencial, se supone que el flujo es irrotacional, es decir, que las pequeñas parcelas de fluido no tienen una tasa neta de rotación. Matemáticamente, esto se expresa mediante el enunciado de que el rotacional del campo vectorial de velocidad es en todas partes igual a cero. Los flujos irrotacionales tienen la propiedad conveniente de que la velocidad se puede expresar como el gradiente de una función escalar llamada potencial. Un flujo representado de esta manera se llama flujo potencial.

En la teoría del flujo potencial, se supone que el flujo es incompresible. La teoría del flujo de potencial incompresible tiene la ventaja de que la ecuación (ecuación de Laplace) a resolver para el potencial es lineal, lo que permite construir soluciones por superposición de otras soluciones conocidas. La ecuación de flujo de potencial incompresible también se puede resolver mediante el mapeo conforme, un método basado en la teoría de funciones de una variable compleja. A principios del siglo XX, antes de que las computadoras estuvieran disponibles, el mapeo conforme se usaba para generar soluciones a la ecuación de flujo potencial incompresible para una clase de formas de superficies aerodinámicas idealizadas, proporcionando algunas de las primeras predicciones teóricas prácticas de la distribución de presión en una superficie aerodinámica de elevación.

Una solución de la ecuación potencial determina directamente solo el campo de velocidad. El campo de presión se deduce del campo de velocidad a través de la ecuación de Bernoulli.

Comparación de un patrón de flujo no elevado alrededor de un flujo de aire; y un patrón de flujo de elevación consistente con la condición de Kutta en la que el flujo deja el borde de seguimiento suavemente

La aplicación de la teoría del flujo potencial a un flujo ascendente requiere un tratamiento especial y una suposición adicional. El problema surge porque la sustentación en un perfil aerodinámico en flujo no viscoso requiere circulación en el flujo alrededor del perfil aerodinámico (consulte "Circulación y el teorema de Kutta-Joukowski" a continuación), pero una sola función potencial que es continua en todo el dominio alrededor el perfil aerodinámico no puede representar un flujo con circulación distinta de cero. La solución a este problema es introducir un corte de rama, una curva o línea desde algún punto de la superficie aerodinámica hasta una distancia infinita, y permitir un salto en el valor del potencial a través del corte. El salto de potencial impone una circulación en el flujo igual al salto de potencial y, por lo tanto, permite representar una circulación distinta de cero. Sin embargo, el salto de potencial es un parámetro libre que no está determinado por la ecuación de potencial ni por las otras condiciones de contorno, por lo que la solución es indeterminada. Existe una solución de flujo potencial para cualquier valor de circulación y cualquier valor de elevación. Una forma de resolver esta indeterminación es imponer la condición de Kutta, que es que, de todas las soluciones posibles, la solución físicamente razonable es aquella en la que el flujo sale del borde de salida sin problemas. Los bocetos aerodinámicos ilustran un patrón de flujo con elevación cero, en el que el flujo rodea el borde de salida y deja la superficie superior por delante del borde de salida, y otro patrón de flujo con elevación positiva, en el que el flujo sale suavemente en el borde de salida en de acuerdo con la condición de Kutta.

Flujo potencial linealizado

Esta es la teoría del flujo potencial con las suposiciones adicionales de que el perfil aerodinámico es muy delgado y el ángulo de ataque es pequeño. La teoría linealizada predice el carácter general de la distribución de la presión del perfil aerodinámico y cómo se ve influenciada por la forma del perfil aerodinámico y el ángulo de ataque, pero no es lo suficientemente precisa para el trabajo de diseño. Para un perfil aerodinámico 2D, tales cálculos se pueden hacer en una fracción de segundo en una hoja de cálculo en una PC.

La circulación y el teorema de Kutta-Joukowski

Componente de circulación del flujo alrededor de una lámina de aire

Cuando una superficie aerodinámica genera sustentación, varios componentes del campo de velocidad general contribuyen a una circulación neta de aire a su alrededor: el flujo ascendente por delante de la superficie aerodinámica, el flujo acelerado por encima, el flujo desacelerado por debajo y el flujo descendente por detrás.

La circulación puede entenderse como la cantidad total de "hilados" (o vorticidad) de un fluido no viscoso alrededor del perfil aerodinámico.

El teorema de Kutta-Joukowski relaciona la sustentación por unidad de ancho de tramo de un perfil aerodinámico bidimensional con este componente de circulación del flujo. Es un elemento clave en una explicación de la sustentación que sigue el desarrollo del flujo alrededor de un perfil aerodinámico cuando el perfil aerodinámico comienza su movimiento desde el reposo y se forma un vórtice inicial que se deja atrás, lo que conduce a la formación de circulación alrededor del perfil aerodinámico. Entonces se deduce la sustentación a partir del teorema de Kutta-Joukowski. Esta explicación es en gran parte matemática, y su progresión general se basa en inferencias lógicas, no en causas y efectos físicos.

El modelo de Kutta-Joukowski no predice cuánta circulación o sustentación producirá un perfil aerodinámico bidimensional. Calcular la elevación por unidad de tramo utilizando Kutta-Joukowski requiere un valor conocido para la circulación. En particular, si se cumple la condición de Kutta, en la que el punto de estancamiento trasero se mueve hacia el borde de salida del perfil aerodinámico y se adhiere allí durante el vuelo, la sustentación se puede calcular teóricamente a través del método de mapeo conforme.

La sustentación generada por un perfil aerodinámico convencional depende tanto de su diseño como de las condiciones de vuelo, como la velocidad de avance, el ángulo de ataque y la densidad del aire. La sustentación se puede aumentar aumentando artificialmente la circulación, por ejemplo, mediante el soplado de la capa límite o el uso de flaps soplados. En el rotor Flettner, toda la superficie aerodinámica es circular y gira sobre un eje transversal para crear la circulación.

Flujo tridimensional

Sección transversal de una combinación de ala-cuerpo de avión que muestra los isobares del flujo de elevación tridimensional

Sección transversal de una combinación de ala-cuerpo de avión que muestra vectores de velocidad del flujo de elevación tridimensional

El flujo alrededor de un ala tridimensional implica importantes problemas adicionales, especialmente en relación con las puntas de las alas. Para un ala de baja relación de aspecto, como un ala delta típica, las teorías bidimensionales pueden proporcionar un modelo pobre y los efectos de flujo tridimensionales pueden dominar. Incluso para alas con una relación de aspecto alta, los efectos tridimensionales asociados con un tramo finito pueden afectar a todo el tramo, no solo cerca de las puntas.

Puntas de ala y distribución longitudinal

El gradiente de presión vertical en las puntas de las alas hace que el aire fluya hacia los lados, desde debajo del ala, luego hacia arriba y hacia atrás sobre la superficie superior. Esto reduce el gradiente de presión en la punta del ala y, por lo tanto, también reduce la sustentación. La sustentación tiende a disminuir en la dirección de la envergadura desde la raíz hasta la punta, y las distribuciones de presión alrededor de las secciones aerodinámicas cambian en consecuencia en la dirección de la envergadura. Las distribuciones de presión en planos perpendiculares a la dirección de vuelo tienden a parecerse a la ilustración de la derecha. Esta distribución de presión que varía a lo largo del tramo se mantiene mediante una interacción mutua con el campo de velocidad. El flujo por debajo del ala se acelera hacia afuera, el flujo por fuera de las puntas se acelera hacia arriba y el flujo por encima del ala se acelera hacia adentro, lo que da como resultado el patrón de flujo que se ilustra a la derecha.

El flujo gira hacia abajo más de lo que habría en un flujo bidimensional con la misma forma aerodinámica y sustentación seccional, y se requiere un ángulo de ataque seccional más alto para lograr la misma sustentación en comparación con un flujo bidimensional flujo. El ala vuela efectivamente en una corriente descendente de su propia creación, como si el flujo de corriente libre estuviera inclinado hacia abajo, con el resultado de que el vector de fuerza aerodinámica total se inclina ligeramente hacia atrás en comparación con lo que sería en dos dimensiones. La componente adicional hacia atrás del vector de fuerza se llama arrastre inducido por sustentación.

Computación Euler de un vórtice de punta rodando desde la hoja de vorticidad

La diferencia en el componente de la velocidad a lo largo de la envergadura por encima y por debajo del ala (entre estar en la dirección interior arriba y en la dirección exterior abajo) persiste en el borde de salida y en la estela corriente abajo. Después de que el flujo abandona el borde de salida, esta diferencia de velocidad tiene lugar a través de una capa de corte relativamente delgada llamada hoja de vórtice.

Sistema de vórtice de herradura

Vista de plano de un ala que muestra el sistema de vórtice de herradura

El flujo de la punta del ala que sale del ala crea un vórtice en la punta. A medida que la hoja de vórtice principal pasa corriente abajo desde el borde de salida, se enrolla en sus bordes exteriores y se fusiona con los vórtices de la punta. La combinación de los vórtices de las puntas de las alas y las láminas de vórtices que los alimentan se denomina estela de vórtices.

Además de la vorticidad en la estela del vórtice posterior, hay vorticidad en la capa límite del ala, denominada "vorticidad unida", que conecta las láminas posteriores de los dos lados del ala en un sistema de vórtice en la forma general de una herradura. La forma de herradura del sistema de vórtice fue reconocida por el pionero aeronáutico británico Lanchester en 1907.

Dada la distribución de la vorticidad ligada y la vorticidad en la estela, la ley de Biot-Savart (una relación de cálculo vectorial) se puede utilizar para calcular la perturbación de la velocidad en cualquier lugar del campo, causada por la sustentación del ala. Las teorías aproximadas para la distribución de sustentación y la resistencia inducida por sustentación de alas tridimensionales se basan en dicho análisis aplicado al sistema de vórtice de herradura del ala. En estas teorías, la vorticidad ligada generalmente se idealiza y se supone que reside en la superficie de comba dentro del ala.

Debido a que la velocidad se deduce de la vorticidad en tales teorías, algunos autores describen la situación para implicar que la vorticidad es la causa de las perturbaciones de la velocidad, usando términos como "la velocidad inducida por el vórtice", por ejemplo. Pero atribuir causa y efecto mecánico entre la vorticidad y la velocidad de esta manera no es consistente con la física. Las perturbaciones de velocidad en el flujo alrededor de un ala son de hecho producidas por el campo de presión.

Manifestaciones de sustentación en el campo lejano

Equilibrio fuerza/momento integrado en flujos de elevación

Los volúmenes de control de diferentes formas que se han utilizado en el análisis del equilibrio de impulso en el flujo 2D alrededor de un flujo de aire elevado. Se supone que el flujo de aire ejerce una fuerza descendente −L' por unidad en el aire, y las proporciones en que esa fuerza se manifiesta como flujos de impulso y diferencias de presión en el límite exterior se indican para cada forma diferente del volumen de control.

El flujo alrededor de un perfil aerodinámico que se eleva debe satisfacer la segunda ley de Newton con respecto a la conservación de la cantidad de movimiento, tanto localmente en cada punto del campo de flujo como en un sentido integrado en cualquier región extendida del flujo. Para una región extendida, la segunda ley de Newton toma la forma del teorema del momento para un volumen de control, donde un volumen de control puede ser cualquier región del flujo elegida para el análisis. El teorema de la cantidad de movimiento establece que la fuerza integrada ejercida en los límites del volumen de control (una integral de superficie) es igual a la tasa de cambio integrada en el tiempo (derivada material) de la cantidad de movimiento de las partículas de fluido que pasan por el interior del volumen de control. Para un flujo constante, esto se puede expresar como la integral de superficie neta del flujo de cantidad de movimiento a través de la frontera.

El flujo de elevación alrededor de un airfoil 2D generalmente se analiza en un volumen de control que rodea completamente el airfoil, de modo que el límite interno del volumen de control es la superficie de la fósfora, donde la fuerza descendente por espacio de unidad $-L'$ se ejerce sobre el fluido por el aire. El límite exterior suele ser un círculo grande o un rectángulo grande. En este límite exterior distante del airfoil, la velocidad y la presión están bien representadas por la velocidad y presión asociada con un flujo uniforme más un vórtice, y el estrés viscoso es insignificante, de modo que la única fuerza que debe ser integrada sobre el límite exterior es la presión. La velocidad de flujo libre se supone generalmente horizontal, con elevación verticalmente hacia arriba, de modo que el impulso vertical es el componente de interés.

Para el caso del aire libre (sin plano), la fuerza $-L'$ ejercido por el flujo de aire en el fluido se manifiesta en parte como flujos de impulso y en parte como diferencias de presión en el límite exterior, en proporciones que dependen de la forma del límite exterior, como se muestra en el diagrama a la derecha. Para un rectángulo horizontal plano que es mucho más largo de lo que es alto, los flujos de impulso vertical a través del frente y la espalda son insignificantes, y el elevador se contabiliza por completo por las diferencias de presión integradas en la parte superior e inferior. Para un cuadrado o círculo, los flujos de impulso y las diferencias de presión representan la mitad del ascensor cada uno. Para un rectángulo vertical que es mucho más alto de lo ancho, las fuerzas de presión desequilibradas en la parte superior e inferior son insignificantes, y el ascensor se contabiliza enteramente por flujos de impulso, con un flujo de impulso ascendente que entra en el volumen de control a través de la parte delantera contando la mitad del ascensor, y un flujo de impulso hacia abajo que sale del volumen de control a través de la contabilidad trasera para la otra mitad.

Los resultados de todos los análisis de volumen de control descritos anteriormente son consistentes con el teorema de Kutta-Joukowski descrito anteriormente. Tanto el volumen de control del rectángulo alto como el del círculo se han utilizado en derivaciones del teorema.

Ascensor reaccionado por sobrepresión en el suelo debajo de un avión

Ilustración de la distribución de la presión superior-que-ambiente en el suelo bajo un avión en vuelo subsónico

Un perfil aerodinámico produce un campo de presión en el aire circundante, como se explica en "El flujo más amplio alrededor del perfil aerodinámico" encima. Las diferencias de presión asociadas con este campo desaparecen gradualmente, volviéndose muy pequeñas a grandes distancias, pero nunca desapareciendo por completo. Debajo del avión, el campo de presión persiste como una perturbación de presión positiva que llega al suelo, formando un patrón de presión ligeramente superior a la ambiental en el suelo, como se muestra a la derecha. Aunque las diferencias de presión son muy pequeñas muy por debajo del avión, se distribuyen en un área amplia y suman una fuerza sustancial. Para un vuelo estable y nivelado, la fuerza integrada debida a las diferencias de presión es igual a la sustentación aerodinámica total del avión y al peso del avión. De acuerdo con la tercera ley de Newton, esta fuerza de presión ejercida sobre el suelo por el aire es igualada por una fuerza hacia arriba igual y opuesta ejercida sobre el aire por el suelo, que compensa toda la fuerza hacia abajo ejercida sobre el aire. por el avión. La fuerza neta debida a la sustentación, que actúa sobre la atmósfera como un todo, es por lo tanto cero y, por lo tanto, no hay una acumulación integrada de momento vertical en la atmósfera, como señaló Lanchester al principio del desarrollo de la aerodinámica moderna.

Contenido relacionado

Más resultados...