Armónicos esféricos

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Funciones matemáticas especiales definidas en la superficie de una esfera

Representaciones visuales de los primeros pocos armónicos esféricos reales. Las porciones azules representan regiones donde la función es positiva, y las porciones amarillas representan donde es negativa. La distancia de la superficie desde el origen indica el valor absoluto de

{displaystyle Y_{ell }^{m}(thetavarphi)}

en dirección angular

(theta,varphi)

En matemáticas y ciencias físicas, los armónicos esféricos son funciones especiales definidas en la superficie de una esfera. A menudo se emplean para resolver ecuaciones diferenciales parciales en muchos campos científicos.

Dado que los armónicos esféricos forman un conjunto completo de funciones ortogonales y, por lo tanto, una base ortonormal, cada función definida en la superficie de una esfera se puede escribir como una suma de estos armónicos esféricos. Esto es similar a las funciones periódicas definidas en un círculo que se pueden expresar como una suma de funciones circulares (seno y coseno) a través de la serie de Fourier. Al igual que los senos y cosenos en la serie de Fourier, los armónicos esféricos pueden organizarse por frecuencia angular (espacial), como se ve en las filas de funciones en la ilustración de la derecha. Además, los armónicos esféricos son funciones base para representaciones irreducibles de SO(3), el grupo de rotaciones en tres dimensiones, y por lo tanto juegan un papel central en la discusión teórica de grupos de SO(3).

Los armónicos esféricos proceden de la solución de la ecuación de Laplace en los dominios esféricos. Las funciones que son soluciones a la ecuación de Laplace se llaman armónicas. A pesar de su nombre, los armónicos esféricos toman su forma más simple en las coordenadas cartesianas, donde se pueden definir como polinomios homogéneos de grado $ell$ dentro $(x,y,z)$ que obedece la ecuación de Laplace. La conexión con las coordenadas esféricas surge inmediatamente si se utiliza la homogeneidad para extraer un factor de dependencia radial $r^ell$ del polinomio de grado mencionado $ell$ ; el factor restante se puede considerar como una función de las coordenadas angulares esféricas $theta$ y $varphi$ sólo, o equivalentemente de la unidad de orientación vector $mathbf {r}$ especificado por estos ángulos. En este entorno, pueden verse como la parte angular de un conjunto de soluciones a la ecuación de Laplace en tres dimensiones, y este punto de vista se toma a menudo como una definición alternativa. Note, sin embargo, que los armónicos esféricos son no funciones en la esfera que son armónicas con respecto al operador Laplace-Beltrami para la métrica redonda estándar en la esfera: las únicas funciones armónicas en este sentido en la esfera son las constantes, ya que las funciones armónicas satisfacen el principio Máximo. Los armónicos esféricos, como funciones en la esfera, son funciones eigen del operador de Laplace-Beltrami (ver la sección Dimensiones superiores infra).

Un conjunto específico de armónicos esféricos, denotados ${displaystyle Y_{ell }^{m}(thetavarphi)}$ o ${displaystyle Y_{ell }^{m}({mathbf {r} })}$ , son conocidos como armónicos esféricos de Laplace, ya que fueron introducidos por primera vez por Pierre Simon de Laplace en 1782. Estas funciones forman un sistema ortogonal, y por lo tanto son básicas para la ampliación de una función general en la esfera tal como se ha indicado anteriormente.

Los armónicos esféricos son importantes en muchas aplicaciones teóricas y prácticas, incluida la representación de campos electrostáticos y electromagnéticos multipolares, configuraciones electrónicas, campos gravitacionales, geoides, los campos magnéticos de cuerpos planetarios y estrellas, y la radiación de fondo cósmico de microondas. En los gráficos por computadora en 3D, los armónicos esféricos desempeñan un papel en una amplia variedad de temas, incluida la iluminación indirecta (oclusión ambiental, iluminación global, transferencia de radiación precalculada, etc.) y el modelado de formas en 3D.

Historia

Pierre-Simon Laplace, 1749-1827

Los armónicos esféricos fueron investigados por primera vez en relación con el potencial Newtoniano de la ley de la gravitación universal de Newton en tres dimensiones. En 1782, Pierre-Simon de Laplace tenía, en su Mécanique Céleste, determinado que el potencial gravitacional ${displaystyle mathbb {R} ^{3}to mathbb {R} }$ en un momento $x$ asociado a un conjunto de masas de puntos $m i$ ubicado en puntos $x i$ fue dado por

{displaystyle V(mathbf {x})=sum _{i}{frac {m_{i}}{|mathbf {x} _{i}-mathbf {x} |}}.}

Cada término de la suma anterior es un potencial newtoniano individual para una masa puntual. Justo antes de ese momento, Adrien-Marie Legendre había investigado la expansión del potencial newtoniano en potencias de $r = | x |$ y $r 1 = | x 1 |$ . Descubrió que si $r \leq r 1$ entonces

{displaystyle {frac {1}{|mathbf {x} _{1}-mathbf {x} |}}=P_{0}(cos gamma){frac {1}{r_{1}}}+P_{1}(cos gamma){frac {r}{r_{1}^{2}}}+P_{2}(cos gamma){frac {r^{2}}{r_{1}^{3}}}+cdots }

Donde $γ$ es el ángulo entre los vectores $x$ y $x 1$ . Funciones ${displaystyle P_{i}:[-1,1]to mathbb {R} }$ son los polinomios Legendre, y pueden ser derivados como un caso especial de armónicos esféricos. Posteriormente, en su memoria de 1782, Laplace investigó estos coeficientes utilizando coordenadas esféricas para representar el ángulo $γ$ entre $x 1$ y $x$ . (Ver Aplicaciones de polinomios Legendre en física para un análisis más detallado.)

En 1867, William Thomson (Lord Kelvin) y Peter Guthrie Tait presentaron los sólidos armónicos esféricos en sus Treatise on Natural Philosophy, y también introdujo el nombre de " armónicos esféricos" para estas funciones. Las armónicas sólidas eran soluciones polinómicas homogéneas ${displaystyle mathbb {R} ^{3}to mathbb {R} }$ de la ecuación de Laplace

{displaystyle {frac {partial ^{2}u}{partial x^{2}}}+{frac {partial ^{2}u}{partial y^{2}}}+{frac {partial ^{2}u}{partial z^{2}}}=0.}

El desarrollo de la serie de Fourier en el siglo XIX hizo posible la solución de una amplia variedad de problemas físicos en dominios rectangulares, como la solución de la ecuación del calor y la ecuación de onda. Esto podría lograrse mediante la expansión de funciones en series de funciones trigonométricas. Mientras que las funciones trigonométricas en una serie de Fourier representan los modos fundamentales de vibración en una cuerda, los armónicos esféricos representan los modos fundamentales de vibración de una esfera de la misma manera. Muchos aspectos de la teoría de las series de Fourier podrían generalizarse tomando expansiones en armónicos esféricos en lugar de funciones trigonométricas. Además, de manera análoga a cómo las funciones trigonométricas pueden escribirse de manera equivalente como exponenciales complejas, los armónicos esféricos también poseían una forma equivalente como funciones de valores complejos. Esto fue una bendición para los problemas que poseían simetría esférica, como los de la mecánica celeste originalmente estudiados por Laplace y Legendre.

La prevalencia de armónicas esféricas ya en la física puso el escenario para su posterior importancia en el nacimiento del siglo XX de la mecánica cuántica. Los armónicos esféricos (valorados complejos) ${displaystyle S^{2}to mathbb {C} }$ son eigenfunctions de la plaza del operador de impulso angular orbital

{displaystyle -ihbar mathbf {r} times nabla}

Armónicos esféricos de Laplace

Real (Laplace) armónicos esféricos

Y_{ell m}

para

{displaystyle ell =0,dots4}

(de arriba a abajo) y

{displaystyle m=0,dotsell }

(izquierda a derecha). Los armónicos Zonal, Sectoriales y Tesseral se representan a lo largo de la columna izquierda-más izquierda, la diagonal principal, y en otros lugares, respectivamente. (El orden negativo armónicos

{displaystyle Y_{ell (-m)}}

se mostraría rota sobre el z axis by

90^{circ }/m

con respecto a los del orden positivo.)

Imagen alternativa para los armónicos esféricos reales

Y_{ell m}

La ecuación de Laplace impone que el Laplaciano de un campo de escalar $f$ es cero. (Aquí se entiende que el campo de escalar es complejo, es decir, corresponder a una función (smooth) ${displaystyle f:mathbb {R} ^{3}to mathbb {C} }$ .) En las coordenadas esféricas esto es:

{displaystyle nabla ^{2}f={frac {1}{r^{2}}}{frac {partial }{partial r}}left(r^{2}{frac {partial f}{partial r}}right)+{frac {1}{r^{2}sin theta }}{frac {partial }{partial theta }}left(sin theta {frac {partial f}{partial theta }}right)+{frac {1}{r^{2}sin ^{2}theta }}{frac {partial ^{2}f}{partial varphi ^{2}}}=0.}

Considere el problema de encontrar soluciones de la forma $f (r, θ, φ) = R (r) Y (θ, φ)$ . Por separación de variables resultan dos ecuaciones diferenciales imponiendo la ecuación de Laplace:

{displaystyle {frac {1}{R}}{frac {d}{dr}}left(r^{2}{frac {dR}{dr}}right)=lambdaqquad {frac {1}{Y}}{frac {1}{sin theta }}{frac {partial }{partial theta }}left(sin theta {frac {partial Y}{partial theta }}right)+{frac {1}{Y}}{frac {1}{sin ^{2}theta }}{frac {partial ^{2}Y}{partial varphi ^{2}}}=-lambda.}

Y

Y () Silencio, φ . Silencio) ↑ φ)

{displaystyle {frac {1}{Phi }}{frac {d^{2}Phi }{dvarphi ^{2}}}=-m^{2}}

{displaystyle lambda sin ^{2}theta +{frac {sin theta }{Theta }}{frac {d}{dtheta }}left(sin theta {frac {dTheta }{dtheta }}right)=m^{2}}

para algún número $m$ . A priori, $m$ es una constante compleja, pero debido a que $Φ$ debe ser una función periódica cuyo periodo divide uniformemente $2 π$ , $m$ es necesariamente un número entero y $Φ$ es una combinación lineal de los exponenciales complejos $e \pm imφ$ . La función solución $Y (θ, φ)$ es regular en los polos de la esfera, donde $θ = 0, π$ . Imponer esta regularidad en la solución $Θ$ de la segunda ecuación en los puntos límite del dominio es un problema de Sturm-Liouville que obliga al parámetro $λ$ para tener la forma $λ = ℓ (ℓ + 1)$ para algún número entero no negativo con $ℓ \geq | m |$ ; esto también se explica a continuación en términos del momento angular orbital. Además, un cambio de variables $t = cos θ$ transforma esta ecuación en la ecuación de Legendre, cuya solución es un múltiplo de el polinomio de Legendre asociado $P m ℓ (cos θ)$ . Finalmente, la ecuación para $R$ tiene soluciones de la forma $R (r) = A r ℓ + B r - ℓ - 1$ ; requerir que la solución sea regular a lo largo de $R 3$ obliga a $B = 0$ .

Aquí se suponía que la solución tenía la forma especial $Y () Silencio, φ . Silencio) ↑ φ)$ . Por un valor dado $l$ , hay $2 l + 1$ soluciones independientes de esta forma, una para cada entero $m$ con $- l \leq m \leq l$ . Estas soluciones angulares ${displaystyle Y_{ell }^{m}:S^{2}to mathbb {C} }$ son un producto de funciones trigonométricas, aquí representado como un complejo exponencial, y polinomios Legendre asociados:

{displaystyle Y_{ell }^{m}(thetavarphi)=Ne^{imvarphi }P_{ell }^{m}(cos {theta })}

que cumplen

{displaystyle r^{2}nabla ^{2}Y_{ell }^{m}(thetavarphi)=-ell (ell +1)Y_{ell }^{m}(thetavarphi).}

Aquí. ${displaystyle Y_{ell }^{m}:S^{2}to mathbb {C} }$ se llama función armónica esférica del grado $l$ y orden $m$ , ${displaystyle P_{ell }^{m}:[-1,1]to mathbb {R} }$ es un polinomio Legendre asociado, $N$ es una constante de normalización, y $Silencio$ y $φ$ representan colatitud y longitud, respectivamente. En particular, las colatitudes $Silencio$ , o ángulo polar, rangos desde $0$ en el Polo Norte, $π /2$ en el Ecuador, $π$ en el Polo Sur, y la longitud $φ$ , o azimut, puede asumir todos los valores con $0 \leq φ 2 π$ . Para un entero fijo $l$ , cada solución $Y () Silencio, φ)$ , ${displaystyle Y:S^{2}to mathbb {C} }$ , del problema eigenvalue

{displaystyle r^{2}nabla ^{2}Y=-ell (ell +1)Y}

{displaystyle Y_{ell }^{m}:S^{2}to mathbb {C} }

r l Y () Silencio, φ)

{displaystyle mathbb {R} ^{3}to mathbb {C} }

2 l + 1

La solución general ${displaystyle f:mathbb {R} ^{3}to mathbb {C} }$ a la ecuación de Laplace ${displaystyle Delta f=0}$ en una bola centrada en el origen es una combinación lineal de las funciones armónicas esféricas multiplicadas por el factor de escala apropiado $r l$ ,

{displaystyle f(r,thetavarphi)=sum _{ell =0}^{infty }sum _{m=-ell }^{ell }f_{ell }^{m}r^{ell }Y_{ell }^{m}(thetavarphi),}

Donde ${displaystyle f_{ell }^{m}in mathbb {C} }$ son constantes y los factores $r l Y l m$ son conocidos comoordinario) armónicos sólidos ${displaystyle mathbb {R} ^{3}to mathbb {C} }$ . Tal expansión es válida en la bola

<math alttext="{displaystyle rr.R=1lim supl l → → JUEGO JUEGO Silenciofl l mSilencio1/l l .{displaystyle R=frac {1}{limsup _{ell to infty. - ¿Qué? - Sí.<img alt="{displaystyle r

Para $R}" xmlns="http://www.w3.org/1998/Math/MathML">r■R{displaystyle r]R}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8971c9610113faec012a76ec2d47fa6235e16d2f" style="vertical-align: -0.338ex; width:5.911ex; height:2.176ex;"/>$ , la armónica sólida con poderes negativos $r$ (irregular armónicos sólidos ${displaystyle mathbb {R} ^{3}setminus {mathbf {0} }to mathbb {C} }$ ) son elegidos en su lugar. En ese caso, es necesario ampliar la solución de las regiones conocidas de la serie Laurent (sobre $r=infty$ ), en lugar de la serie Taylor (sobre $r=0$ ) utilizado anteriormente, para coincidir con los términos y encontrar coeficientes de expansión serie ${displaystyle f_{ell }^{m}in mathbb {C} }$ .

Momento angular orbital

En la mecánica cuántica, los armónicos esféricos de Laplace se entienden en términos del momento angular orbital

{displaystyle mathbf {L} =-ihbar (mathbf {x} times mathbf {nabla })=L_{x}mathbf {i} +L_{y}mathbf {j} +L_{z}mathbf {k}.}

▪

▪ = 1

{displaystyle {begin{aligned}mathbf {L} ^{2}&=-r^{2}nabla ^{2}+left(r{frac {partial }{partial r}}+1right)r{frac {partial }{partial r}}\&=-{frac {1}{sin theta }}{frac {partial }{partial theta }}sin theta {frac {partial }{partial theta }}-{frac {1}{sin ^{2}theta }}{frac {partial ^{2}}{partial varphi ^{2}}}.end{aligned}}}

{displaystyle {begin{aligned}L_{z}&=-ileft(x{frac {partial }{partial y}}-y{frac {partial }{partial x}}right)\&=-i{frac {partial }{partial varphi }}.end{aligned}}}

Estos operadores conmutan y son operadores autoadjuntos densamente definidos en el espacio ponderado de Hilbert de funciones f integrables al cuadrado con respecto a la distribución normal como la función de peso en R³:

<math alttext="{displaystyle {frac {1}{(2pi)^{3/2}}}int _{mathbb {R} ^{3}}|f(x)|^{2}e^{-|x|^{2}/2},dx1()2π π )3/2∫ ∫ R3Silenciof()x)Silencio2e− − SilencioxSilencio2/2dx.JUEGO JUEGO .{displaystyle {frac {1}{2pi)}int _{mathbb [R] ^{3},dx buscadoinfty.]<img alt="{displaystyle {frac {1}{(2pi)^{3/2}}}int _{mathbb {R} ^{3}}|f(x)|^{2}e^{-|x|^{2}/2},dx

L²

Si $Y$ es una función propia conjunta de $L 2$ y $L z$ , entonces por definición

{displaystyle {begin{aligned}mathbf {L} ^{2}Y&=lambda Y\L_{z}Y&=mYend{aligned}}}

mλmYφπ

{displaystyle mathbf {L} ^{2}=L_{x}^{2}+L_{y}^{2}+L_{z}^{2}}

L_xL_Sí.L_z

λ \geq m 2

Denote este espacio propio conjunto mediante $E λ, m$ , y defina los operadores de subida y bajada mediante

{displaystyle {begin{aligned}L_{+}&=L_{x}+iL_{y}\L_{-}&=L_{x}-iL_{y}end{aligned}}}

L +

L -

L 2

L +

L -

L z

{displaystyle {mathfrak {sl}}_{2}(mathbb {C})}

{displaystyle [L_{z},L_{+}]=L_{+},quad [L_{z},L_{-}]=-L_{-},quad [L_{+},L_{-}]=2L_{z}.}

L + : E λ, m \to E λ, m + 1

L - : E λ, m \to E λ, m -1

L k + : E λ, m \to E λ, m + k

λ \geq m 2

Y ▪ E λ, m

k

{displaystyle L_{+}^{k}Y=0.}

{displaystyle L_{-}L_{+}=mathbf {L} ^{2}-L_{z}^{2}-L_{z}}

{displaystyle 0=L_{-}L_{+}^{k}Y=(lambda -(m+k)^{2}-(m+k))Y.}

λ = l () l + 1)

l = m + k

Lo anterior ha sido todo trabajado en la representación de la coordinación esférica, ${displaystyle langle thetavarphi |lmrangle =Y_{l}^{m}(thetavarphi)}$ pero se puede expresar más abstractamente en la base completa ortonormal de kot.

Representación de polinomios armónicos

Las armónicas esféricas se pueden expresar como la restricción a la esfera unitaria de ciertas funciones polinómicas ${displaystyle mathbb {R} ^{3}to mathbb {C} }$ . Específicamente, decimos que una función polinomial (valorada por complejos) ${displaystyle p:mathbb {R} ^{3}to mathbb {C} }$ es homogénea de grado $ell$ si

{displaystyle p(lambda mathbf {x})=lambda ^{ell }p(mathbf {x})}

{displaystyle lambda in mathbb {R} }

{displaystyle xin mathbb {R} ^{3}}

p

{displaystyle Delta p=0,}

Delta

ell

{displaystyle mathbf {A} _{ell }=left{{text{harmonic polynomials }}mathbb {R} ^{3}to mathbb {C} {text{ that are homogeneous of degree }}ell right}.}

Por ejemplo, cuando $ell =1$ , ${displaystyle mathbf {A} _{1}}$ es sólo el espacio tridimensional de todas las funciones lineales ${displaystyle mathbb {R} ^{3}to mathbb {C} }$ , ya que cualquier función de este tipo es automáticamente armónica. Mientras tanto, cuando $ell =2$ , tenemos un espacio de 5 dimensiones:

{displaystyle mathbf {A} _{2}=operatorname {span} _{mathbb {C} }(x_{1}x_{2},,x_{1}x_{3},,x_{2}x_{3},,x_{1}^{2}-x_{2}^{2},,x_{1}^{2}-x_{3}^{2}).}

Para cualquier $ell$ , el espacio ${displaystyle mathbf {H} _{ell }}$ of spherical harmonics of degree $ell$ es sólo el espacio de restricciones a la esfera $S^{2}$ de los elementos ${displaystyle mathbf {A} _{ell }}$ . Como se sugiere en la introducción, esta perspectiva es presumiblemente el origen del término “ armónico esférico” (es decir, la restricción a la esfera de una función armónica).

Por ejemplo, para cualquier ${displaystyle cin mathbb {C} }$ la fórmula

{displaystyle p(x_{1},x_{2},x_{3})=c(x_{1}+ix_{2})^{ell }}

ell

{displaystyle mathbb {R} ^{3}to mathbb {C} }

x_{3}

p

(r,thetavarphi)

r=1

{displaystyle p(thetavarphi)=csin(theta)^{ell }(cos(varphi)+isin(varphi))^{ell },}

{displaystyle p(thetavarphi)=cleft({sqrt {1-cos ^{2}(theta)}}right)^{ell }e^{iell varphi }.}

{displaystyle P_{ell }^{ell }}

{displaystyle Y_{ell }^{ell }(thetavarphi).}

Convenios

Ortogonalidad y normalización

Varias normalizaciones diferentes son de uso común para las funciones armónicas esféricas de Laplace ${displaystyle S^{2}to mathbb {C} }$ . A lo largo de la sección, utilizamos la convención estándar para $0}" xmlns="http://www.w3.org/1998/Math/MathML">m■0{displaystyle m confía0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/501173910e6da8425b4e9d44a4e8643620bc2464" style="vertical-align: -0.338ex; width:6.301ex; height:2.176ex;"/>$ (ver polinomios Legendre asociados)

{displaystyle P_{ell }^{-m}=(-1)^{m}{frac {(ell -m)!}{(ell +m)!}}P_{ell }^{m}}

Parcela de la armónica esférica

{displaystyle Y_{ell }^{m}(thetavarphi)}

con

ell =2

m=1

{displaystyle varphi =pi }

en el plano complejo desde

{displaystyle -2-2i}

{displaystyle 2+2i}

con colores creados con Mathematica 13.1 función ComplexPlot3D

En acústica, los armónicos esféricos de Laplace se definen generalmente como (esta es la convención utilizada en este artículo)

{displaystyle Y_{ell }^{m}(thetavarphi)={sqrt {{frac {(2ell +1)}{4pi }}{frac {(ell -m)!}{(ell +m)!}}}},P_{ell }^{m}(cos {theta }),e^{imvarphi }}

{displaystyle Y_{ell }^{m}(thetavarphi)=(-1)^{m}{sqrt {{frac {(2ell +1)}{4pi }}{frac {(ell -m)!}{(ell +m)!}}}},P_{ell }^{m}(cos {theta }),e^{imvarphi }}

Donde ${displaystyle P_{ell }^{m}}$ se asocian polinomios Legendre sin la fase Condon–Shortley (para evitar contar la fase dos veces).

En ambas definiciones, los armónicos esféricos son ortonormales

{displaystyle int _{theta =0}^{pi }int _{varphi =0}^{2pi }Y_{ell }^{m},Y_{ell '}^{m'}{}^{*},dOmega =delta _{ell ell '},delta _{mm'},}

δ ij

d Ω = pecado Silencio) dφ d)

{displaystyle int {|Y_{ell }^{m}|^{2}dOmega }=1.}

Las disciplinas de geodesia y análisis espectral utilizan

{displaystyle Y_{ell }^{m}(thetavarphi)={sqrt {{(2ell +1)}{frac {(ell -m)!}{(ell +m)!}}}},P_{ell }^{m}(cos {theta }),e^{imvarphi }}

que poseen poder unitario

{displaystyle {frac {1}{4pi }}int _{theta =0}^{pi }int _{varphi =0}^{2pi }Y_{ell }^{m},Y_{ell '}^{m'}{}^{*}dOmega =delta _{ell ell '},delta _{mm'}.}

La comunidad magnética, por el contrario, utiliza armónicos seminormalizados de Schmidt.

{displaystyle Y_{ell }^{m}(thetavarphi)={sqrt {frac {(ell -m)!}{(ell +m)!}}},P_{ell }^{m}(cos {theta }),e^{imvarphi }}

que tienen la normalización

{displaystyle int _{theta =0}^{pi }int _{varphi =0}^{2pi }Y_{ell }^{m},Y_{ell '}^{m'}{}^{*}dOmega ={frac {4pi }{(2ell +1)}}delta _{ell ell '},delta _{mm'}.}

En la mecánica cuántica, esta normalización también se usa a veces y se denomina normalización de Racah en honor a Giulio Racah.

Se puede demostrar que todas las funciones armónicas esféricas normalizadas anteriores satisfacen

{displaystyle Y_{ell }^{m}{}^{*}(thetavarphi)=(-1)^{m}Y_{ell }^{-m}(thetavarphi),}

donde el superíndice $*$ denota una conjugación compleja. Alternativamente, esta ecuación se deriva de la relación de las funciones armónicas esféricas con la matriz D de Wigner.

Fase Condón-Shortley

Una fuente de confusión con la definición de las funciones armónicas esféricas se refiere a un factor de fase $(-1)^{m}$ , comúnmente conocido como la fase Condon-Shortley en la literatura mecánica cuántica. En la comunidad de mecánica cuántica, es práctica común incluir este factor de fase en la definición de los polinomios Legendre asociados, o anexarlo a la definición de las funciones armónicas esféricas. No hay necesidad de utilizar la fase Condon–Shortley en la definición de las funciones armónicas esféricas, pero incluso puede simplificar algunas operaciones mecánicas cuánticas, especialmente la aplicación de operadores de elevación y reducción. Las comunidades geodesia y magnética nunca incluyen el factor de fase Condon-Shortley en sus definiciones de las funciones armónicas esféricas ni en las de los polinomios Legendre asociados.

Forma real

Una base real de armónicos esféricos ${displaystyle Y_{ell m}:S^{2}to mathbb {R} }$ puede definirse en términos de sus análogos complejos ${displaystyle Y_{ell }^{m}:S^{2}to mathbb {C} }$ por configuración

<math alttext="{displaystyle {begin{aligned}Y_{ell m}&={begin{cases}{dfrac {i}{sqrt {2}}}left(Y_{ell }^{m}-(-1)^{m},Y_{ell }^{-m}right)&{text{if}} m0.end{cases}}\&={begin{cases}{dfrac {i}{sqrt {2}}}left(Y_{ell }^{-|m|}-(-1)^{m},Y_{ell }^{|m|}right)&{text{if}} m0.end{cases}}\&={begin{cases}{sqrt {2}},(-1)^{m},Im [{Y_{ell }^{|m|}}]&{text{if}} m0.end{cases}}end{aligned}}}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">Yl l m={}i2()Yl l m− − ()− − 1)mYl l − − m)sim.0Yl l 0sim=012()Yl l − − m+()− − 1)mYl l m)sim■0.={}i2()Yl l − − SilenciomSilencio− − ()− − 1)mYl l SilenciomSilencio)sim.0Yl l 0sim=012()Yl l − − SilenciomSilencio+()− − 1)mYl l SilenciomSilencio)sim■0.={}2()− − 1)mI I [Yl l SilenciomSilencio]sim.0Yl l 0sim=02()− − 1)mR R [Yl l m]sim■0.{displaystyle {begin{aligned}Y_{ell m} {begin{cases}{dfrac {fnK} {fnK}}m} {fnK} {fnfnMicrosoft Sans Serif} {f}}m}} {f}f}fnK}f}fnf}fnf}\fnK}f}fnKfnKf}fnKf}f}f}f}fnKf}fnKfnKfnKfnKfnKfnKf}f}fnKfnKfnKfnKfnKfnKf}f}fnKfnKfnKf}fnKf}fnKfnKfnKfnKfnKf}fnKfnKfnKfnKfnKf}fnKf}fnK ### {fnMicrosoft ## }{0} {text{if} m=0\{dfrac {1}{sqrt {2}}left(Y_{ell }{-m}+(-1)^{m},Y_{ell }}{m}right) Sentirse en un momento en que se tratase de una forma de hacer un trabajo. ##### {begin{cases}{dfrac {I}{sqrt {2}}}left(Y_{ell }{- perpetuam upon}-(-1)^{m},Y_{ell }^{Principo de la vida}right) ### {fnMicrosoft ## }{0} {text{if} m=0\{dfrac {1}{sqrt {2}}}left(Y_{ell }{- perpetuam upon}+(-1)^{m},Y_{ell }^{Principe a la vida)}derecha) ######### {begin{cases}{sqrt {2},(-1)^{m},Im [{Y_{ell }{m sometida}}}} {text{if}f}\fnMicros} ### {fnMicrosoft ## }{0} {text{if} ################################################################################################################################################################################################################################################################ m título.<img alt="{displaystyle {begin{aligned}Y_{ell m}&={begin{cases}{dfrac {i}{sqrt {2}}}left(Y_{ell }^{m}-(-1)^{m},Y_{ell }^{-m}right)&{text{if}} m0.end{cases}}\&={begin{cases}{dfrac {i}{sqrt {2}}}left(Y_{ell }^{-|m|}-(-1)^{m},Y_{ell }^{|m|}right)&{text{if}} m0.end{cases}}\&={begin{cases}{sqrt {2}},(-1)^{m},Im [{Y_{ell }^{|m|}}]&{text{if}} m0.end{cases}}end{aligned}}}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/281f6a87023810f7fa9a80d46805c8ad18597fe8" style="vertical-align: -20.171ex; width:48.627ex; height:41.509ex;"/>

{displaystyle Y_{ell }^{m}:S^{2}to mathbb {C} }

{displaystyle Y_{ell m}:S^{2}to mathbb {R} }

<math alttext="{displaystyle Y_{ell }^{m}={begin{cases}{dfrac {1}{sqrt {2}}}left(Y_{ell |m|}-iY_{ell-|m|}right)&{text{if}} m0.end{cases}}}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">Yl l m={}12()Yl l SilenciomSilencio− − iYl l ,− − SilenciomSilencio)sim.0Yl l 0sim=0()− − 1)m2()Yl l SilenciomSilencio+iYl l ,− − SilenciomSilencio)sim■0.{displaystyle Y... ### {m}={begin{cases}{dfrac {1}{sqrt {2}}left(Y_{ell Нани ваный }-iY_{ell- sobre la vida eterna}right) [4pt]Y_{text{if} m=0[4pt]{=0}{m}{m}{sqrt {2}}left(Y_{ell Нани ваный }+iY_{ell- sobre la vida eterna}right) m título.<img alt="{displaystyle Y_{ell }^{m}={begin{cases}{dfrac {1}{sqrt {2}}}left(Y_{ell |m|}-iY_{ell-|m|}right)&{text{if}} m0.end{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/27971bab040e0ab0b2533f34865c0a6225cb12d2" style="vertical-align: -7.813ex; margin-bottom: -0.192ex; width:45.14ex; height:17.176ex;"/>

Los verdaderos armónicos esféricos ${displaystyle Y_{ell m}:S^{2}to mathbb {R} }$ a veces se conoce como tesseral spherical harmonics. Estas funciones tienen las mismas propiedades de la ortonormalidad que las complejas ${displaystyle Y_{ell }^{m}:S^{2}to mathbb {C} }$ arriba. Los verdaderos armónicos esféricos $Y_{ell m}$ con $m ■ 0$ se dice que son de tipo cosino, y los con $m 0$ de tipo sine. La razón de esto se puede ver escribiendo las funciones en términos de los polinomios Legendre como

<math alttext="{displaystyle Y_{ell m}={begin{cases}left(-1right)^{m}{sqrt {2}}{sqrt {{dfrac {2ell +1}{4pi }}{dfrac {(ell -|m|)!}{(ell +|m|)!}}}};P_{ell }^{|m|}(cos theta) sin(|m|varphi)&{text{if }}m0,.end{cases}}}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">Yl l m={}()− − 1)m22l l +14π π ()l l − − SilenciomSilencio)!()l l +SilenciomSilencio)!Pl l SilenciomSilencio()#⁡ ⁡ Silencio Silencio )pecado⁡ ⁡ ()SilenciomSilencioφ φ )sim.02l l +14π π Pl l m()#⁡ ⁡ Silencio Silencio )sim=0()− − 1)m22l l +14π π ()l l − − m)!()l l +m)!Pl l m()#⁡ ⁡ Silencio Silencio )#⁡ ⁡ ()mφ φ )sim■0.{displaystyle Y... m}={begin{cases}left(-1right)}{m}{sqrt {2}{4}{sqrt {dfrac {2ell +1}{4i}{dfrac {ell - sometidam sometida)}{(ell + perpetuam perpetua!}}};P_{ell }{mfnf} {ccc} {cH00}cH00} {4}} {ccH00}}ccH00cH00ccH00}}ccccH00}}cccH00ccH00cccH00ccH00cH00cH00cH00cH00cH00}cH00}}}cH00ccH00ccH00cH00cH00cH00cH00cH00cH00cH00}cH00cH00cH00}}ccc {fnMicrosoft Sans Serif}m=0[4pt]left(-1right)}{m}{sqrt {2}{sqrt {dfrac {2ell +1}{4pi}{dfrac {(ell -m)}{(ell +m)}}}};P_{ell } {m} {cos theta)cos(mvarphi)} {text{if} {f}fnf} {f}f} {fnMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMientras)}fnMientras, mientras, mientras, mientras, mientras, mientras, mientras, mientras, mientras, mientras, yo estaba en mientras, yo estaba en mientras, yo estaba en mientras, yo estaba en mientras, - ¿Qué?<img alt="{displaystyle Y_{ell m}={begin{cases}left(-1right)^{m}{sqrt {2}}{sqrt {{dfrac {2ell +1}{4pi }}{dfrac {(ell -|m|)!}{(ell +|m|)!}}}};P_{ell }^{|m|}(cos theta) sin(|m|varphi)&{text{if }}m0,.end{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/20ccbde100d451bfe2fff46127a1e31705c95351" style="vertical-align: -11.005ex; width:72.45ex; height:23.176ex;"/>

Los mismos factores de seno y coseno también se pueden ver en la siguiente subsección que trata sobre la representación cartesiana.

Vea aquí una lista de armónicos esféricos reales hasta e incluyendo $ell =4$ , que se puede ver que es consistente con la salida de las ecuaciones anteriores.

Uso en química cuántica

Como se sabe a partir de las soluciones analíticas para el átomo de hidrógeno, las funciones propias de la parte angular de la función de onda son armónicos esféricos. Sin embargo, las soluciones de la ecuación de Schrödinger no relativista sin términos magnéticos pueden hacerse realidad. Esta es la razón por la cual las formas reales se usan ampliamente en funciones básicas para la química cuántica, ya que los programas no necesitan usar álgebra compleja. Aquí, es importante señalar que las funciones reales abarcan el mismo espacio que las complejas.

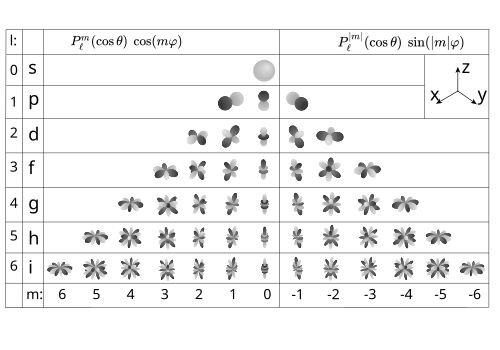
Por ejemplo, como se puede ver en la tabla de armónicos esféricos, lo habitual $p$ funciones ( $ell =1$ ) son complejas y mezclar direcciones de eje, pero las versiones reales son esencialmente sólo $x$ , $Sí.$ , y $z$ .

Armónicos esféricos en forma cartesiana

Los complejos armónicos esféricos $Y_{ell }^{m}$ dar lugar a los armónicos sólidos al extenderse $S^{2}$ a todos $mathbb{R} ^{3}$ como función homogénea del grado $ell$ , i.e. setting

{displaystyle R_{ell }^{m}(v):=|v|^{ell }Y_{ell }^{m}left({frac {v}{|v|}}right)}

{displaystyle R_{ell }^{m}}

ell

SO(3)

{displaystyle R_{ell }^{m}}

La función generadora de Herglotz

Si se aprueba la convención mecánica cuántica ${displaystyle Y_{ell }^{m}:S^{2}to mathbb {C} }$ , entonces

{displaystyle e^{v{mathbf {a} }cdot {mathbf {r} }}=sum _{ell =0}^{infty }sum _{m=-ell }^{ell }{sqrt {frac {4pi }{2ell +1}}}{frac {r^{ell }v^{ell }{lambda ^{m}}}{sqrt {(ell +m)!(ell -m)!}}}Y_{ell }^{m}(mathbf {r} /r).}

mathbf {r}

{displaystyle (x,y,z)in mathbb {R} ^{3}}

{displaystyle r=|mathbf {r} |}

{displaystyle {mathbf {a} }={mathbf {hat {z}} }-{frac {lambda }{2}}left({mathbf {hat {x}} }+i{mathbf {hat {y}} }right)+{frac {1}{2lambda }}left({mathbf {hat {x}} }-i{mathbf {hat {y}} }right).}

{displaystyle mathbf {a} }

${displaystyle mathbf {a} =[{frac {1}{2}}({frac {1}{lambda }}-lambda),-{frac {i}{2}}({frac {1}{lambda }}+lambda),1].}$

La propiedad esencial de $mathbf {a}$ es que es nulo:

{displaystyle mathbf {a} cdot mathbf {a} =0.}

Basta tomar $v$ y $lambda$ como parámetros reales. Al nombrar esta función generadora después de Herglotz, seguimos a Courant " Hilbert 1962, §VII.7, que acreditan notas inéditas por él para su descubrimiento.

Esencialmente todas las propiedades de los armónicos esféricos pueden derivarse de esta función generadora. Un beneficio inmediato de esta definición es que si el vector $mathbf {r}$ es reemplazado por el operador de vectores de giro mecánico cuántico $mathbf {J}$ , tal que ${displaystyle {mathcal {Y}}_{ell }^{m}({mathbf {J} })}$ es el análogo del operador del armónico sólido ${displaystyle r^{ell }Y_{ell }^{m}(mathbf {r} /r)}$ , se obtiene una función generadora para un conjunto estandarizado de operadores de tensores esféricos, ${displaystyle {mathcal {Y}}_{ell }^{m}({mathbf {J} })}$ :

{displaystyle e^{v{mathbf {a} }cdot {mathbf {J} }}=sum _{ell =0}^{infty }sum _{m=-ell }^{ell }{sqrt {frac {4pi }{2ell +1}}}{frac {v^{ell }{lambda ^{m}}}{sqrt {(ell +m)!(ell -m)!}}}{mathcal {Y}}_{ell }^{m}({mathbf {J} }).}

El paralelismo de las dos definiciones garantiza que ${displaystyle {mathcal {Y}}_{ell }^{m}}$ 's transformar bajo rotaciones (ver abajo) de la misma manera que el $Y_{ell}^m$ 's, que a su vez garantiza que son operadores de tensores esféricos, $T^{(k)}_q$ , con ${displaystyle k={ell }}$ y ${displaystyle q=m}$ , obedeciendo todas las propiedades de tales operadores, como el teorema de composición Clebsch-Gordan, y el teorema Wigner-Eckart. Son, además, un conjunto estandarizado con una escala fija o normalización.

Forma cartesiana separada

La definición herglotziana produce polinomios que pueden, si uno desea, ser más factorizados en un polinomio de $z$ y otro de $x$ y $y$ , como sigue (fase Condon-Shortley):

0.}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">rl l ()Yl l mYl l − − m)=[2l l +14π π ]1/2▪ ▪ ̄ ̄ l l m()z)()()− − 1)m()Am+iBm)()Am− − iBm)),m■0.{displaystyle r^{ell Y... {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}0.}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/066f9cfa96f2c4550337a93bf73d61517362c834" style="vertical-align: -3.171ex; width:68.743ex; height:7.509ex;"/>

m = 0

{displaystyle r^{ell },Y_{ell }^{0}equiv {sqrt {frac {2ell +1}{4pi }}}{bar {Pi }}_{ell }^{0}.}

{displaystyle A_{m}(x,y)=sum _{p=0}^{m}{binom {m}{p}}x^{p}y^{m-p}cos left((m-p){frac {pi }{2}}right),}

{displaystyle B_{m}(x,y)=sum _{p=0}^{m}{binom {m}{p}}x^{p}y^{m-p}sin left((m-p){frac {pi }{2}}right),}

{displaystyle {bar {Pi }}_{ell }^{m}(z)=left[{frac {(ell -m)!}{(ell +m)!}}right]^{1/2}sum _{k=0}^{leftlfloor (ell -m)/2rightrfloor }(-1)^{k}2^{-ell }{binom {ell }{k}}{binom {2ell -2k}{ell }}{frac {(ell -2k)!}{(ell -2k-m)!}};r^{2k};z^{ell -2k-m}.}

m=0

{displaystyle {bar {Pi }}_{ell }^{0}(z)=sum _{k=0}^{leftlfloor ell /2rightrfloor }(-1)^{k}2^{-ell }{binom {ell }{k}}{binom {2ell -2k}{ell }};r^{2k};z^{ell -2k}.}

El factor ${bar {Pi }}_{ell }^{m}(z)$ es esencialmente el polinomio Legendre asociado $P_{ell }^{m}(cos theta)$ , y los factores ${displaystyle (A_{m}pm iB_{m})}$ son esencialmente ${displaystyle e^{pm imvarphi }}$ .

Ejemplos

Utilizar las expresiones para ${bar {Pi }}_{ell }^{m}(z)$ , ${displaystyle A_{m}(x,y)}$ , y ${displaystyle B_{m}(x,y)}$ enumerado explícitamente arriba obtenemos:

{displaystyle Y_{3}^{1}=-{frac {1}{r^{3}}}left[{tfrac {7}{4pi }}cdot {tfrac {3}{16}}right]^{1/2}left(5z^{2}-r^{2}right)left(x+iyright)=-left[{tfrac {7}{4pi }}cdot {tfrac {3}{16}}right]^{1/2}left(5cos ^{2}theta -1right)left(sin theta e^{ivarphi }right)}

{displaystyle Y_{4}^{-2}={frac {1}{r^{4}}}left[{tfrac {9}{4pi }}cdot {tfrac {5}{32}}right]^{1/2}left(7z^{2}-r^{2}right)left(x-iyright)^{2}=left[{tfrac {9}{4pi }}cdot {tfrac {5}{32}}right]^{1/2}left(7cos ^{2}theta -1right)left(sin ^{2}theta e^{-2ivarphi }right)}

Formas reales

Usando las ecuaciones anteriores para formar los verdaderos armónicos esféricos, se ve que para $0}" xmlns="http://www.w3.org/1998/Math/MathML">m■0{displaystyle m confía0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/501173910e6da8425b4e9d44a4e8643620bc2464" style="vertical-align: -0.338ex; width:6.301ex; height:2.176ex;"/>$ sólo el $A_{m}$ términos (cosinas) están incluidos, y $<math alttext="{displaystyle mm.0{displaystyle m won0} <img alt="m$ sólo el $B_{m}$ los términos (sines) se incluyen:

0.}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">rl l ()Yl l mYl l − − m)=2l l +12π π ▪ ▪ ̄ ̄ l l m()z)()AmBm),m■0.{displaystyle r^{ell Y... ###Y_{ell -m}end{pmatrix}={sqrt {frac {2ell +1}{2pi {fnMicrosoft Sans} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif}} {f}} {fnfn}}} {fnfnfnfnfnfnfnfnf}}} {fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfn\fnfnfnfnfnfnfnfnfnfnfnfnfnfnfn\fnfn Pi }_{ell } {m}(z){begin{pmatrix}A_{m}B_{m}end{pmatrix}}qquad m título.0.}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d1e9817a27f969539b995a26a4c64cce170fd796" style="vertical-align: -2.505ex; width:50.464ex; height:6.509ex;"/>

{displaystyle r^{ell },Y_{ell 0}equiv {sqrt {frac {2ell +1}{4pi }}}{bar {Pi }}_{ell }^{0}.}

Casos y valores especiales

Cuando $m=0$ , los armónicos esféricos ${displaystyle Y_{ell }^{m}:S^{2}to mathbb {C} }$ reducir a lo ordinario Polinomios legendarios: ${displaystyle Y_{ell }^{0}(thetavarphi)={sqrt {frac {2ell +1}{4pi }}}P_{ell }(cos theta).}$
Cuando ${displaystyle m=pm ell }$ , ${displaystyle Y_{ell }^{pm ell }(thetavarphi)={frac {(mp 1)^{ell }}{2^{ell }ell !}}{sqrt {frac {(2ell +1)!}{4pi }}}sin ^{ell }theta ,e^{pm iell varphi },}$ o más simplemente en coordenadas cartesianas, ${displaystyle r^{ell }Y_{ell }^{pm ell }({mathbf {r} })={frac {(mp 1)^{ell }}{2^{ell }ell !}}{sqrt {frac {(2ell +1)!}{4pi }}}(xpm iy)^{ell }.}$
En el polo norte, donde ${displaystyle theta =0}$ , y $varphi$ es indefinido, todos los armónicos esféricos excepto aquellos con $m=0$ desaparecer: ${displaystyle Y_{ell }^{m}(0,varphi)=Y_{ell }^{m}({mathbf {z} })={sqrt {frac {2ell +1}{4pi }}}delta _{m0}.}$

Propiedades de simetría

Los armónicos esféricos tienen propiedades profundas y consecuentes bajo las operaciones de inversión espacial (paridad) y rotación.

Paridad

Los armónicos esféricos tienen paridad definida. Es decir, son incluso o extraños con respecto a la inversión sobre el origen. La inversión está representada por el operador ${displaystyle PPsi (mathbf {r})=Psi (-mathbf {r})}$ . Entonces, como se puede ver de muchas maneras (quizás simplemente de la función generadora Herglotz), con $mathbf {r}$ ser un vector unitario,

{displaystyle Y_{ell }^{m}(-mathbf {r})=(-1)^{ell }Y_{ell }^{m}(mathbf {r}).}

En términos de ángulos esféricos, la paridad transforma un punto con coordenadas ${displaystyle {thetavarphi }}$ a ${displaystyle {pi -thetapi +varphi }}$ . La declaración de la paridad de los armónicos esféricos es entonces

{displaystyle Y_{ell }^{m}(thetavarphi)to Y_{ell }^{m}(pi -thetapi +varphi)=(-1)^{ell }Y_{ell }^{m}(thetavarphi)}

(1)- l + m

(1)- m

(1)- l

La paridad sigue siendo válida para los armónicos esféricos reales y para los armónicos esféricos en dimensiones superiores: aplicar un punto de reflexión a un armónico esférico de grado $ℓ$ cambia el signo por un factor de $(-1) ℓ$ .

Rotaciones

La rotación de una función esférica real con

m = 0

l = 3

. Los coeficientes no son iguales al Wigner D-matrices, ya que las funciones reales se muestran, pero se pueden obtener re-descomponiendo las funciones complejas

Considere una rotación $mathcal R$ sobre el origen que envía la unidad vector $mathbf {r}$ a ${mathbf r}'$ . Bajo esta operación, una armónica esférica de grado $ell$ y orden $m$ se transforma en una combinación lineal de armónicos esféricos del mismo grado. Eso es,

{displaystyle Y_{ell }^{m}({mathbf {r} }')=sum _{m'=-ell }^{ell }A_{mm'}Y_{ell }^{m'}({mathbf {r} }),}

{displaystyle A_{mm'}}

{displaystyle (2ell +1)}

mathcal R

{displaystyle Y_{ell }^{m}({mathbf {r} }')=sum _{m'=-ell }^{ell }[D_{mm'}^{(ell)}({mathcal {R}})]^{*}Y_{ell }^{m'}({mathbf {r} }),}

{displaystyle D_{mm'}^{(ell)}({mathcal {R}})^{*}}

{mathbf r}'

phi _{0}

{displaystyle Y_{ell }^{m}({mathbf {r} }')=Y_{ell }^{m}({mathbf {r} })e^{imphi _{0}}.}

El comportamiento de rotación de los armónicos esféricos es quizás su característica por excelencia desde el punto de vista de la teoría del grupo. El $Y_{ell }^{m}$ 's de grado $ell$ proporcionar una base de funciones para la representación irreductible del grupo SO(3) de dimensión ${displaystyle (2ell +1)}$ . Muchos hechos sobre armónicos esféricos (como el teorema de adición) que se prueban mano de obra utilizando los métodos de análisis adquieren pruebas más simples y significado más profundo utilizando los métodos de simetría.

Expansión de armónicos esféricos

Los armónicos esféricos de Laplace ${displaystyle Y_{ell }^{m}:S^{2}to mathbb {C} }$ forma un conjunto completo de funciones ortonormales y así forman una base ortonormal del espacio Hilbert de funciones cuadradas ${displaystyle L_{mathbb {C} }^{2}(S^{2})}$ . En la esfera de unidad $S^{2}$ , cualquier función cuadrada ${displaystyle f:S^{2}to mathbb {C} }$ por lo tanto se puede ampliar como una combinación lineal de estos:

{displaystyle f(thetavarphi)=sum _{ell =0}^{infty }sum _{m=-ell }^{ell }f_{ell }^{m},Y_{ell }^{m}(thetavarphi).}

Esta expansión es válida en el sentido de convergencia cuadrática media (convergencia en L2 de la esfera), lo que quiere decir que

{displaystyle lim _{Nto infty }int _{0}^{2pi }int _{0}^{pi }left|f(thetavarphi)-sum _{ell =0}^{N}sum _{m=-ell }^{ell }f_{ell }^{m}Y_{ell }^{m}(thetavarphi)right|^{2}sin theta ,dtheta ,dvarphi =0.}

Los coeficientes de expansión son análogos a los coeficientes de Fourier y se pueden obtener multiplicando la ecuación anterior por el conjugado complejo de un armónico esférico, integrando sobre el ángulo sólido Ω y utilizando las relaciones de ortogonalidad anteriores. Esto se justifica rigurosamente por la teoría básica del espacio de Hilbert. Para el caso de armónicos ortonormalizados, esto da:

{displaystyle f_{ell }^{m}=int _{Omega }f(thetavarphi),Y_{ell }^{m*}(thetavarphi),dOmega =int _{0}^{2pi }dvarphi int _{0}^{pi },dtheta ,sin theta f(thetavarphi)Y_{ell }^{m*}(thetavarphi).}

Si los coeficientes decaen en ℓ lo suficientemente rápido (por ejemplo, exponencialmente), entonces la serie también converge uniformemente a f.

Función cuadrada integrada ${displaystyle f:S^{2}to mathbb {R} }$ también se puede ampliar en términos de los verdaderos armónicos ${displaystyle Y_{ell m}:S^{2}to mathbb {R} }$ arriba como una suma

{displaystyle f(thetavarphi)=sum _{ell =0}^{infty }sum _{m=-ell }^{ell }f_{ell m},Y_{ell m}(thetavarphi).}

La convergencia de la serie se mantiene de nuevo en el mismo sentido, a saber, los verdaderos armónicos esféricos ${displaystyle Y_{ell m}:S^{2}to mathbb {R} }$ forma un conjunto completo de funciones ortonormales y así forman una base ortonormal del espacio Hilbert de funciones cuadradas ${displaystyle L_{mathbb {R} }^{2}(S^{2})}$ . El beneficio de la expansión en términos de las funciones armónicas reales $Y_{ell m}$ es que para funciones reales ${displaystyle f:S^{2}to mathbb {R} }$ los coeficientes de expansión ${displaystyle f_{ell m}}$ están garantizados para ser reales, mientras que sus coeficientes ${displaystyle f_{ell }^{m}}$ en su expansión en términos de $Y_{ell}^m$ (considerándolos como funciones ${displaystyle f:S^{2}to mathbb {C} supset mathbb {R} }$ No tienen esa propiedad.

Análisis de espectro

Espectro de potencia en procesamiento de señales

La potencia total de una función f se define en la literatura de procesamiento de señales como la integral de la función al cuadrado, dividida por el área de su dominio. Utilizando las propiedades de ortonormalidad de las funciones armónicas esféricas de potencia unitaria real, es sencillo verificar que la potencia total de una función definida en la esfera unitaria está relacionada con sus coeficientes espectrales mediante una generalización del teorema de Parseval (aquí, el teorema se establece para los armónicos seminormalizados de Schmidt, la relación es ligeramente diferente para los armónicos ortonormales):

{displaystyle {frac {1}{4,pi }}int _{Omega }|f(Omega)|^{2},dOmega =sum _{ell =0}^{infty }S_{f!f}(ell),}

{displaystyle S_{f!f}(ell)={frac {1}{2ell +1}}sum _{m=-ell }^{ell }|f_{ell m}|^{2}}

se define como el espectro de potencia angular (para armónicos seminormalizados de Schmidt). De manera similar, se puede definir la potencia cruzada de dos funciones como

{displaystyle {frac {1}{4,pi }}int _{Omega }f(Omega),g^{ast }(Omega),dOmega =sum _{ell =0}^{infty }S_{fg}(ell),}

{displaystyle S_{fg}(ell)={frac {1}{2ell +1}}sum _{m=-ell }^{ell }f_{ell m}g_{ell m}^{ast }}

se define como el espectro de potencia cruzada. Si las funciones $f$ y $g$ tienen una media cero (es decir,, los coeficientes espectrales $f 00$ y $g 00$ son cero), entonces $S ff (ℓ)$ y $S fg (ℓ)$ representan las contribuciones a la varianza y covarianza de la función para el grado $ℓ$ , respectivamente. Es común que el espectro de potencia (cruzado) se aproxime bien mediante una ley de potencia de la forma

{displaystyle S_{f!f}(ell)=C,ell ^{beta }.}

Cuando $β = 0$ , el espectro es "blanco" ya que cada grado posee igual poder. Cuando $β < 0$ , el espectro se denomina "rojo" ya que hay más potencia en los grados bajos con longitudes de onda largas que en los grados más altos. Finalmente, cuando $β > 0$ , el espectro se denomina "azul". La condición sobre el orden de crecimiento de $S ff (ℓ)$ está relacionado con el orden de diferenciabilidad de $f$ en la siguiente sección.

Propiedades de diferenciabilidad

También se pueden entender las propiedades de diferenciabilidad de la función original $f$ en términos de las asintóticas de $S ff (ℓ)$ . En particular, si $S ff (ℓ)$ decae más rápido que cualquier función racional de $ℓ$ como $ℓ \to \infty$ , entonces $f$ es infinitamente diferenciable. Si, además, $S ff (ℓ)$ decae exponencialmente, entonces $f$ es realmente analítico real en la esfera.

La técnica general es utilizar la teoría de los espacios de Sobolev. Declaraciones relacionadas con el crecimiento de $S ff (ℓ)$ a diferenciabilidad son entonces similares a resultados análogos sobre el crecimiento de los coeficientes de la serie de Fourier. Específicamente, si

<math alttext="{displaystyle sum _{ell =0}^{infty }(1+ell ^{2})^{s}S_{ff}(ell).. l l =0JUEGO JUEGO ()1+l l 2)sSff()l l ).JUEGO JUEGO ,{displaystyle sum _{ell =0}{infty }(1+ell ^{2})^{s}S_{ff}(ell)traducidoinfty}<img alt="{displaystyle sum _{ell =0}^{infty }(1+ell ^{2})^{s}S_{ff}(ell)

f

H s () S 2)

f

{displaystyle S_{ff}(ell)=O(ell ^{-s})quad {rm {{as }ell to infty }}}

s

Propiedades algebraicas

Teorema de la adición

Un resultado matemático de considerable interés y uso se llama el adición teorema para armónicos esféricos. Dados dos vectores $r$ y $r'$ , con coordenadas esféricas $(r,thetavarphi)$ y ${displaystyle (r',theta ',varphi ')}$ , respectivamente, el ángulo $gamma$ entre ellos se da por la relación

{displaystyle cos gamma =cos theta 'cos theta +sin theta sin theta 'cos(varphi -varphi ')}

El teorema de la suma establece

{displaystyle P_{ell }(mathbf {x} cdot mathbf {y})={frac {4pi }{2ell +1}}sum _{m=-ell }^{ell }Y_{ell m}(mathbf {y}),Y_{ell m}^{*}(mathbf {x})quad forall ,ell in mathbb {N} _{0};forall ,mathbf {x}mathbf {y} in mathbb {R} ^{3}colon ;|mathbf {x} |_{2}=|mathbf {y} |_{2}=1,,}

()1)

donde $P ℓ$ es el polinomio de Legendre de grado $ℓ$ . Esta expresión es válida tanto para armónicos reales como complejos. El resultado se puede probar analíticamente, usando las propiedades del núcleo de Poisson en la bola unitaria, o geométricamente aplicando una rotación al vector y para que apunte a lo largo de la z -eje, y luego calcular directamente el lado derecho.

En particular, cuando $x = y$ , esto da el teorema de Unsöld

{displaystyle sum _{m=-ell }^{ell }Y_{ell m}^{*}(mathbf {x}),Y_{ell m}(mathbf {x})={frac {2ell +1}{4pi }}}

# 2 Silencio + pecado 2 Silencio = 1

En la expansión (1), el lado izquierdo ${displaystyle P_{ell }(mathbf {x} cdot mathbf {y})}$ es un múltiplo constante del grado $l$ armónico esférico zonal. Desde esta perspectiva, uno tiene la siguiente generalización a dimensiones superiores. Vamos $Y j$ ser una base ortonormal arbitraria del espacio $H l$ grado $l$ armónicos esféricos en $n$ - Esfera. Entonces... $Z_{mathbf {x} }^{(ell)}$ , el grado $l$ zonal armónico correspondiente al vector $x$ , descompuestos como

{displaystyle Z_{mathbf {x} }^{(ell)}({mathbf {y} })=sum _{j=1}^{dim(mathbf {H} _{ell })}{overline {Y_{j}({mathbf {x} })}},Y_{j}({mathbf {y} })}

()2)

Además, la armónica zonal $Z_{mathbf {x} }^{(ell)}({mathbf {y} })$ se da como un múltiple constante del polinomio Gegenbauer adecuado:

{displaystyle Z_{mathbf {x} }^{(ell)}({mathbf {y} })=C_{ell }^{((n-2)/2)}({mathbf {x} }cdot {mathbf {y} })}

()3)

Combinando (2) y (3) da (1) en la dimensión $n = 2$ cuando $x$ y $y$ se representan en coordenadas esféricas. Finalmente, evaluar en $x = y$ da la identidad funcional

{displaystyle {frac {dim mathbf {H} _{ell }}{omega _{n-1}}}=sum _{j=1}^{dim(mathbf {H} _{ell })}|Y_{j}({mathbf {x} })|^{2}}

\cdot n -1

Regla de contracción

Otra identidad útil expresa el producto de dos armónicos esféricos como una suma de armónicos esféricos

{displaystyle Y_{a,alpha }left(thetavarphi right)Y_{b,beta }left(thetavarphi right)={sqrt {frac {left(2a+1right)left(2b+1right)}{4pi }}}sum _{c=0}^{infty }sum _{gamma =-c}^{c}left(-1right)^{gamma }{sqrt {2c+1}}{begin{pmatrix}a&b&c\alpha &beta &-gamma end{pmatrix}}{begin{pmatrix}a&b&c\0&0&0end{pmatrix}}Y_{c,gamma }left(thetavarphi right).}

c

gamma

Coeficientes de Clebsch-Gordan

Los coeficientes de Clebsch-Gordan son los coeficientes que aparecen en la expansión del producto de dos armónicos esféricos en términos de los propios armónicos esféricos. Hay una variedad de técnicas disponibles para hacer esencialmente el mismo cálculo, incluido el símbolo de Wigner 3-jm, los coeficientes de Racah y las integrales de Slater. De manera abstracta, los coeficientes de Clebsch-Gordan expresan el producto tensorial de dos representaciones irreducibles del grupo de rotación como una suma de representaciones irreducibles: adecuadamente normalizados, los coeficientes son entonces las multiplicidades.

Visualización de los armónicos esféricos

Representación esquemática

Y_{ell m}

en la esfera de unidad y sus líneas nodal.

{displaystyle Re [Y_{ell m}]}

es igual a 0 a lo largo

m

grandes círculos pasando por los polos, y a lo largo l−m círculos de igual latitud. La función cambia de signo cada vez que cruza una de estas líneas.

Parcela de color 3D de los armónicos esféricos de grado

n = 5

. Note que

n = l

Los armónicos esféricos de Laplace $Y_{ell }^{m}$ se puede visualizar considerando sus "líneas nodal", es decir, el conjunto de puntos en la esfera donde ${displaystyle Re [Y_{ell }^{m}]=0}$ , o alternativamente donde ${displaystyle Im [Y_{ell }^{m}]=0}$ . Líneas nominales $Y_{ell }^{m}$ se componen de l círculos: hay $Silencio m Silencio$ círculos a lo largo de longitudes y l− La vidamSilencio círculos a lo largo de latitudes. Uno puede determinar el número de líneas nodal de cada tipo contando el número de ceros de $Y_{ell }^{m}$ en el $theta$ y $varphi$ direcciones, respectivamente. Considerando $Y_{ell }^{m}$ como función de $theta$ , los componentes reales e imaginarios de los polinomios Legendre asociados cada uno posee l− La vidamSilencio ceros, cada uno dando lugar a una "línea de latitud" nodal. Por otro lado, considerando $Y_{ell }^{m}$ como función de $varphi$ , el pecado trigonométrico y las funciones cos poseen 2 vidasmSilencio ceros, cada uno de los cuales da lugar a una "línea de longitud" nodal.

Cuando el orden armónico esférico m es cero (parte superior izquierda de la figura), las funciones armónicas esféricas no dependen de la longitud y se denominan zonal. Tales armónicos esféricos son un caso especial de funciones esféricas zonales. Cuando $ℓ = | m |$ (parte inferior derecha de la figura), no hay cruces por cero en la latitud y las funciones se denominan sectoriales. Para los demás casos, las funciones marcan la esfera y se denominan tesseral.

Más armónicos esféricos generales de grado $l$ no son necesariamente los de la base de Laplace $Y_{ell }^{m}$ , y sus conjuntos de nodal pueden ser de un tipo bastante general.

Lista de armónicos esféricos

Expresiones analíticas para las primeras pocas armónicas ortonormalizadas de Laplace ${displaystyle Y_{ell }^{m}:S^{2}to mathbb {C} }$ que utilizan la convención de la fase Condon-Shortley:

{displaystyle Y_{0}^{0}(thetavarphi)={frac {1}{2}}{sqrt {frac {1}{pi }}}}

{displaystyle {begin{aligned}Y_{1}^{-1}(thetavarphi)&={frac {1}{2}}{sqrt {frac {3}{2pi }}},sin theta ,e^{-ivarphi }\Y_{1}^{0}(thetavarphi)&={frac {1}{2}}{sqrt {frac {3}{pi }}},cos theta \Y_{1}^{1}(thetavarphi)&={frac {-1}{2}}{sqrt {frac {3}{2pi }}},sin theta ,e^{ivarphi }end{aligned}}}

{displaystyle {begin{aligned}Y_{2}^{-2}(thetavarphi)&={frac {1}{4}}{sqrt {frac {15}{2pi }}},sin ^{2}theta ,e^{-2ivarphi }\Y_{2}^{-1}(thetavarphi)&={frac {1}{2}}{sqrt {frac {15}{2pi }}},sin theta ,cos theta ,e^{-ivarphi }\Y_{2}^{0}(thetavarphi)&={frac {1}{4}}{sqrt {frac {5}{pi }}},(3cos ^{2}theta -1)\Y_{2}^{1}(thetavarphi)&={frac {-1}{2}}{sqrt {frac {15}{2pi }}},sin theta ,cos theta ,e^{ivarphi }\Y_{2}^{2}(thetavarphi)&={frac {1}{4}}{sqrt {frac {15}{2pi }}},sin ^{2}theta ,e^{2ivarphi }end{aligned}}}

Dimensiones superiores

Las armónicas esféricas clásicas se definen como funciones de valor complejo en la esfera unitaria $S^{2}$ dentro de tres dimensiones Espacio euclidiano $mathbb{R} ^{3}$ . Los armónicos esféricos se pueden generalizar al espacio euclidiano de mayor dimensión $mathbb {R} ^{n}$ de la siguiente manera: ${displaystyle S^{n-1}to mathbb {C} }$ . Vamos P_l denotar el espacio de polinomios homogéneos de alto valor complejo $l$ dentro $n$ variables reales, aquí consideradas como funciones ${displaystyle mathbb {R} ^{n}to mathbb {C} }$ . Es decir, un polinomio $p$ está dentro $P l$ siempre que sea real ${displaystyle lambda in mathbb {R} }$ , uno tiene

{displaystyle p(lambda mathbf {x})=lambda ^{ell }p(mathbf {x}).}

Sea A_ℓ el subespacio de P_ℓ que consta de todos los polinomios armónicos:

{displaystyle mathbf {A} _{ell }:={pin mathbf {P} _{ell },mid ,Delta p=0},.}

H_l

{displaystyle S^{n-1}:={mathbf {x} in mathbb {R} ^{n},mid ,left|xright|=1}}

A l

{displaystyle mathbf {H} _{ell }:=left{f:S^{n-1}to mathbb {C} ,mid ,{text{ for some }}pin mathbf {A} _{ell },,f(mathbf {x})=p(mathbf {x}){text{ for all }}mathbf {x} in S^{n-1}right}.}

Las siguientes propiedades se mantienen:

La suma de los espacios $H l$ es denso en el conjunto ${displaystyle C(S^{n-1})}$ de funciones continuas $S^{{n-1}}$ con respecto a la topología uniforme, por el teorema de Piedra-Weierstrass. Como resultado, la suma de estos espacios es también densa en el espacio $L 2 () S n -1)$ de funciones cuadradas-integrables en la esfera. Así cada función cuadrada-integrable en la esfera se descompone únicamente en una serie de armónicos esféricos, donde la serie converge en la $L 2$ sentido.
Para todos $f ▪ H l$ , uno tiene ${displaystyle Delta _{S^{n-1}}f=-ell (ell +n-2)f.}$ Donde $Δ S n -1$ es el operador de Laplace-Beltrami en $S n -1$ . Este operador es el análogo de la parte angular del Laplaciano en tres dimensiones; a saber, el Laplaciano en $n$ dimensiones descompuestas ${displaystyle nabla ^{2}=r^{1-n}{frac {partial }{partial r}}r^{n-1}{frac {partial }{partial r}}+r^{-2}Delta _{S^{n-1}}={frac {partial ^{2}}{partial r^{2}}}+{frac {n-1}{r}}{frac {partial }{partial r}}+r^{-2}Delta _{S^{n-1}}}$
A continuación del teorema de Stokes y la propiedad anterior que los espacios $H l$ son ortogonales con respecto al producto interno de $L 2 () S n -1)$ . Es decir, ${displaystyle int _{S^{n-1}}f{bar {g}},mathrm {d} Omega =0}$ para $f ▪ H l$ y $g ▪ H k$ para $k ل l$ .
Por el contrario, los espacios $H l$ son precisamente los eigenespacios de $Δ S n -1$ . En particular, una aplicación del teorema espectral al potencial de Riesz $Delta _{S^{n-1}}^{-1}$ da otra prueba de que los espacios $H l$ son dos veces ortogonal y completo en $L 2 () S n -1)$ .
Cada polinomio homogéneo $p ▪ P l$ puede ser escrito en forma única ${displaystyle p(x)=p_{ell }(x)+|x|^{2}p_{ell -2}+cdots +{begin{cases}|x|^{ell }p_{0}&ell {rm { even}}\|x|^{ell -1}p_{1}(x)&ell {rm { odd}}end{cases}}}$ Donde $p j ▪ A j$ . En particular, ${displaystyle dim mathbf {H} _{ell }={binom {n+ell -1}{n-1}}-{binom {n+ell -3}{n-1}}.}$

Se puede construir inductivamente una base ortogonal de armónicos esféricos en dimensiones superiores mediante el método de separación de variables, resolviendo el problema de Sturm-Liouville para el laplaciano esférico

{displaystyle Delta _{S^{n-1}}=sin ^{2-n}varphi {frac {partial }{partial varphi }}sin ^{n-2}varphi {frac {partial }{partial varphi }}+sin ^{-2}varphi Delta _{S^{n-2}}}

φSⁿ⁻¹

{displaystyle Y_{ell _{1},dots ell _{n-1}}(theta _{1},dots theta _{n-1})={frac {1}{sqrt {2pi }}}e^{iell _{1}theta _{1}}prod _{j=2}^{n-1}{}_{j}{bar {P}}_{ell _{j}}^{ell _{j-1}}(theta _{j})}

Silencio l 1 ■ \leq l 2 \leq \leq \leq l n -1

- l n -1 () l n -1 + n -2)

{displaystyle {}_{j}{bar {P}}_{L}^{ell }(theta)={sqrt {{frac {2L+j-1}{2}}{frac {(L+ell +j-2)!}{(L-ell)!}}}}sin ^{frac {2-j}{2}}(theta)P_{L+{frac {j-2}{2}}}^{-left(ell +{frac {j-2}{2}}right)}(cos theta),.}

Conexión con la teoría de la representación

El espacio $H ℓ$ de armónicos esféricos de grado $ℓ$ es una representación del grupo de simetría de rotaciones alrededor de un punto (SO(3)) y su doble cubierta SU(2). De hecho, las rotaciones actúan sobre la esfera bidimensional y, por lo tanto, también sobre $H ℓ$ por composición de funciones

{displaystyle psi mapsto psi circ rho ^{-1}}

↑

***

H l

Los elementos de $H l$ surgen como las restricciones a la esfera de los elementos $A l$ : polinomios armónicos homogéneos de grado $l$ en el espacio Euclideano tridimensional $R 3$ . Por polarización $↑ ▪ A l$ , hay coeficientes $psi _{i_{1}dots i_{ell }}$ simétrico en los índices, determinado únicamente por el requisito

{displaystyle psi (x_{1},dotsx_{n})=sum _{i_{1}dots i_{ell }}psi _{i_{1}dots i_{ell }}x_{i_{1}}cdots x_{i_{ell }}.}

↑

psi _{i_{1}dots i_{ell }}

SO(3)

H l

l

Más generalmente, las declaraciones análogas se mantienen en dimensiones superiores: el espacio $H ℓ$ de armónicos esféricos en la n-esfera es la representación irreducible de $SO(n +1)$ correspondiente a la simetría sin rastro $ℓ$ -tensores. Sin embargo, mientras que cada representación tensorial irreducible de $SO(2)$ y $SO(3)$ es de este tipo, los grupos ortogonales especiales en dimensiones superiores tienen representaciones irreducibles adicionales que no surgen de esta manera.

Los grupos ortogonales especiales tienen representaciones de espín adicionales que no son representaciones de tensor y típicamente no son armónicos esféricos. Una excepción son las representaciones de espín de SO(3): estrictamente hablando, estas son representaciones de la doble cubierta SU(2) de SO(3). A su vez, SU(2) se identifica con el grupo de cuaterniones unitarios, por lo que coincide con la 3-esfera. Los espacios de armónicos esféricos en la 3-esfera son ciertas representaciones de espín de SO(3), con respecto a la acción por multiplicación cuaterniónica.

Conexión con armónicos hemisféricos

Los armónicos esféricos se pueden separar en dos conjuntos de funciones. Una de ellas son las funciones hemisféricas (HSH), ortogonales y completas en el hemisferio. Otro son los armónicos hemisféricos complementarios (CHSH).

Generalizaciones

Las simetrías que conservan el ángulo de las dos esferas se describen mediante el grupo de transformaciones de Möbius PSL(2,C). Con respecto a este grupo, la esfera es equivalente a la habitual esfera de Riemann. El grupo PSL(2,C) es isomorfo al (propio) grupo de Lorentz, y su acción sobre las dos esferas concuerda con la acción del grupo de Lorentz sobre la esfera celeste en el espacio de Minkowski. El análogo de los armónicos esféricos para el grupo de Lorentz viene dado por la serie hipergeométrica; además, los armónicos esféricos se pueden reexpresar en términos de la serie hipergeométrica, ya que $SO(3) = PSU(2)$ es un subgrupo de $PSL(2, C)$ .

De manera más general, las series hipergeométricas se pueden generalizar para describir las simetrías de cualquier espacio simétrico; en particular, se pueden desarrollar series hipergeométricas para cualquier grupo de Lie.

Contenido relacionado

Más resultados...