Árbol rojo-negro
En informática, un árbol rojo-negro es una especie de árbol binario de búsqueda autoequilibrado. Cada nodo almacena un bit adicional que representa el "color" ("rojo" o "negro"), que se utiliza para garantizar que el árbol permanezca equilibrado durante las inserciones y eliminaciones.
Cuando se modifica el árbol, el nuevo árbol se reorganiza y "repinta" para restaurar las propiedades colorantes que limitan el desequilibrio que puede llegar a tener el árbol en el peor de los casos. Las propiedades están diseñadas de tal manera que esta reorganización y cambio de color se puede realizar de manera eficiente.
El (re-)balancing no es perfecto, pero garantiza la búsqueda en O()log n){displaystyle O(log n)} tiempo, donde n{displaystyle n} es el número de entradas (o llaves) en el árbol. Las operaciones de inserción y eliminación, junto con la reordenación de árboles y recoloración, también se realizan en O()log n){displaystyle O(log n)} tiempo.
El seguimiento del color de cada nodo requiere solo un bit de información por nodo porque solo hay dos colores. El árbol no contiene ningún otro dato específico de que sea un árbol rojo-negro, por lo que su huella de memoria es casi idéntica a la de un árbol de búsqueda binario clásico (sin color). En algunos casos, el bit adicional de información se puede almacenar sin costo de memoria adicional.
Historia
En 1972, Rudolf Bayer inventó una estructura de datos que era un caso especial de orden 4 de un árbol B. Estos árboles mantuvieron todos los caminos desde la raíz hasta la hoja con el mismo número de nodos, creando árboles perfectamente equilibrados. Sin embargo, no eran árboles de búsqueda binarios. Bayer los llamó "árbol B binario simétrico" en su artículo y más tarde se hicieron populares como 2–3–4 árboles o simplemente 2–4 árboles.
En un artículo de 1978, "Un marco dicromático para árboles equilibrados", Leonidas J. Guibas y Robert Sedgewick derivaron el árbol rojo-negro del árbol B binario simétrico. El color "rojo" fue elegido porque era el color de mejor apariencia producido por la impresora láser a color disponible para los autores mientras trabajaban en Xerox PARC. Otra respuesta de Guibas afirma que fue por los bolígrafos rojos y negros que tenían a su disposición para dibujar los árboles.
En 1993, Arne Andersson introdujo la idea de un árbol inclinado a la derecha para simplificar las operaciones de inserción y eliminación.
En 1999, Chris Okasaki mostró cómo hacer que la operación de inserción sea puramente funcional. Su función de equilibrio necesitaba cuidar solo 4 casos desequilibrados y un caso equilibrado predeterminado.
El algoritmo original utilizó 8 casos desequilibrados, pero Cormen et al. (2001) lo redujo a 6 casos no balanceados. Sedgewick demostró que la operación de inserción se puede implementar en solo 46 líneas de código Java. En 2008, Sedgewick propuso el árbol rojo-negro inclinado a la izquierda, aprovechando la idea de Andersson que simplificó las operaciones de inserción y eliminación. Sedgewick originalmente permitía nodos cuyos dos hijos fueran rojos, lo que hacía que sus árboles fueran más como 2–3–4 árboles, pero luego se agregó esta restricción, haciendo que los árboles nuevos fueran más como 2–3 árboles. Sedgewick implementó el algoritmo de inserción en solo 33 líneas, acortando significativamente sus 46 líneas de código originales.
Terminología
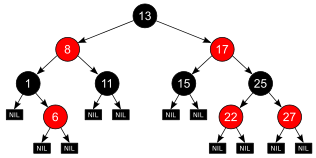
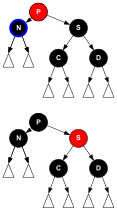
Un árbol rojo-negro es un tipo especial de árbol de búsqueda binaria que se utiliza en informática para organizar piezas de datos comparables, como fragmentos de texto o números (como, por ejemplo, los números de las figuras 1 y 2). Los nodos que transportan claves y/o datos se denominan con frecuencia "nodos internos", pero para que esto sea muy específico, también se denominan nodos no NIL en este artículo.
Los nodos de las hojas de los árboles rojo-negro ( NIL en la figura 1) no contienen claves o datos. Estas "hojas" no es necesario que sean individuos explícitos en la memoria de la computadora: un puntero NULL puede —como en todas las estructuras de datos de árbol binario— codificar el hecho de que no hay un nodo secundario en esta posición en el nodo (padre). Sin embargo, por su posición en el árbol, estos objetos están en relación con otros nodos que son relevantes para la estructura RB, puede tener un nodo padre, hermano (es decir, el otro hijo del padre), tío, incluso sobrino; y puede ser hijo, pero nunca padre de otro nodo.
No es realmente necesario atribuir un "color" a estos objetos de final de ruta, porque la condición "es NIL o BLACK" está implícito en la condición "es NIL" (ver también este comentario).
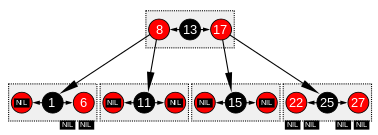
La Figura 2 muestra conceptualmente el mismo árbol rojo-negro sin estas hojas NIL. Para llegar a la misma noción de camino, uno tiene que notar que, p. 3 rutas atraviesan el nodo 1, es decir, una ruta a través de 1izquierda más 2 rutas adicionales a través de 1derecha, es decir, los caminos a través de 6izquierda y 6derecha. De esta manera, estos extremos de los caminos también son puntos de acoplamiento para que se inserten nuevos nodos, totalmente equivalentes a las hojas NIL de la figura 1.
Por otro lado, para ahorrar una cantidad marginal de tiempo de ejecución, estas (posiblemente muchas) hojas NIL pueden implementarse como punteros a un nodo centinela único (y negro) (en lugar de punteros de valor NULL).
Como conclusión, el hecho de que un hijo no exista (no es un nodo verdadero, no contiene datos) puede especificarse en todos los casos con el mismo puntero NULL o como el mismo puntero a un nodo centinela. A lo largo de este artículo, cualquiera de las opciones se denomina nodo NIL y tiene el valor constante NIL.
La profundidad negra de un nodo se define como el número de nodos negros desde la raíz hasta ese nodo (es decir, el número de ancestros negros). La altura negra de un árbol rojo-negro es el número de nodos negros en cualquier camino desde la raíz hasta las hojas, que, por el requisito 4, es constante (alternativamente, podría definirse como el negro profundidad de cualquier nudo hoja). La altura negra de un nodo es la altura negra del subárbol enraizado por él. En este artículo, la altura negra de un nodo NIL se establecerá en 0, porque su subárbol está vacío como se sugiere en la figura 2, y la altura del árbol también es 0.
Propiedades
Además de los requisitos impuestos a un árbol de búsqueda binaria, un árbol rojo-negro debe cumplir lo siguiente:
- Cada nodo es rojo o negro.
- Todos los nodos NIL (figura 1) se consideran negros.
- Un nodo rojo no tiene un niño rojo.
- Cada camino de un nodo dado a cualquiera de sus nodos descendientes del NIL pasa por el mismo número de nodos negros.
Algunos autores, p. Cormen &erio; al., afirman "la raíz es negra" como quinto requisito; pero no Mehlhorn & Sanders o Sedgewick & Wayne. Dado que la raíz siempre se puede cambiar de rojo a negro, esta regla tiene poco efecto en el análisis. Este artículo también lo omite, porque perturba ligeramente los algoritmos recursivos y las pruebas.
Como ejemplo, cada árbol binario perfecto que consta solo de nodos negros es un árbol rojo-negro.
Las operaciones de solo lectura, como la búsqueda o el cruce de árboles, no afectan ninguno de los requisitos. Por otro lado, las operaciones de modificación insert y delete mantienen fácilmente los requisitos 1 y 2, pero con respecto a los otros requisitos, se debe realizar un esfuerzo adicional para evitar la introducción de una violación del requisito 3, denominada violación roja, o del requisito 4, llamado violación negra.
Los requisitos imponen una propiedad crítica de los árboles rojo-negro: el camino de la raíz a la hoja más lejana no es más del doble que el camino de la raíz a la hoja más cercana. El resultado es que el árbol es equilibrado de altura. Puesto que las operaciones tales como la inserción, eliminación y determinación de valores requieren el peor tiempo proporcional a la altura h{displaystyle h} del árbol, este borde superior en la altura permite que los árboles rojo-negro sean eficientes en el peor de los casos, es decir, logarítmico en el número n{displaystyle n} de entradas, es decir. h▪ ▪ O()log n){displaystyle hin O(log n)}, que no es el caso de los árboles de búsqueda binaria ordinarios. Para una prueba matemática ver sección Prueba de límites.
Los árboles rojo-negro, como todos los árboles de búsqueda binaria, permiten un acceso secuencial bastante eficiente (por ejemplo, la traversal en orden, es decir: en el orden Izquierda–Root–Right) de sus elementos. Pero soportan también el acceso directo asintotically óptimo a través de un traversal de raíz a hoja, dando lugar a O()log n){displaystyle O(log n)} Tiempo de búsqueda.
Analogía a árboles B de orden 4
Un árbol rojo-negro tiene una estructura similar a un árbol B de orden 4, donde cada nodo puede contener entre 1 y 3 valores y (en consecuencia) entre 2 y 4 punteros secundarios. En tal árbol B, cada nodo contendrá solo un valor que coincida con el valor en un nodo negro del árbol rojo-negro, con un valor opcional antes y/o después en el mismo nodo, ambos coincidentes con un nodo rojo equivalente de el árbol rojo-negro.
Una forma de ver esta equivalencia es "subir" los nodos rojos en una representación gráfica del árbol rojo-negro, de modo que se alineen horizontalmente con su nodo negro principal, creando juntos un grupo horizontal. En el árbol B, o en la representación gráfica modificada del árbol rojo-negro, todos los nodos de hoja están a la misma profundidad.
El árbol rojo-negro es estructuralmente equivalente a un árbol B de orden 4, con un factor de relleno mínimo del 33 % de los valores por grupo con una capacidad máxima de 3 valores.
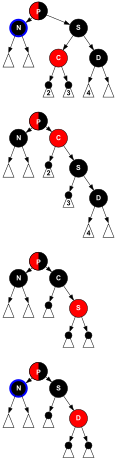
Sin embargo, este tipo de árbol B es aún más general que un árbol rojo-negro, ya que permite la ambigüedad en una conversión de árbol rojo-negro: se pueden producir múltiples árboles rojo-negro a partir de un árbol B equivalente de orden 4 (ver figura 3). Si un clúster de árbol B contiene solo 1 valor, es el mínimo, negro y tiene dos punteros secundarios. Si un grupo contiene 3 valores, entonces el valor central será negro y cada valor almacenado en sus lados será rojo. Sin embargo, si el grupo contiene dos valores, cualquiera de ellos puede convertirse en el nodo negro en el árbol rojo-negro (y el otro será rojo).
Entonces, el árbol B de orden 4 no mantiene cuál de los valores contenidos en cada grupo es el árbol negro raíz para todo el grupo y el padre de los otros valores en el mismo grupo. A pesar de esto, las operaciones sobre árboles rojo-negro son más económicas en el tiempo porque no hay que mantener el vector de valores. Puede ser costoso si los valores se almacenan directamente en cada nodo en lugar de almacenarse por referencia. Los nodos de árbol B, sin embargo, son más económicos en espacio porque no es necesario almacenar el atributo de color para cada nodo. En su lugar, debe saber qué ranura en el vector de clúster se utiliza. Si los valores se almacenan por referencia, p. objetos, se pueden usar referencias nulas y, por lo tanto, el clúster se puede representar mediante un vector que contiene 3 ranuras para punteros de valor más 4 ranuras para referencias secundarias en el árbol. En ese caso, el árbol B puede ser más compacto en la memoria, mejorando la localidad de los datos.
Se puede hacer la misma analogía con árboles B con órdenes más grandes que pueden ser estructuralmente equivalentes a un árbol binario de colores: solo necesita más colores. Suponga que agrega azul, luego el árbol azul-rojo-negro definido como árboles rojo-negro pero con la restricción adicional de que dos nodos sucesivos en la jerarquía no serán azules y todos los nodos azules serán hijos de un nodo rojo, entonces se vuelve equivalente a un árbol B cuyos grupos tendrán como máximo 7 valores en los siguientes colores: azul, rojo, azul, negro, azul, rojo, azul (Para cada grupo, habrá como máximo 1 nodo negro, 2 nodos rojos y 4 nodos azules).
Para volúmenes moderados de valores, las inserciones y eliminaciones en un árbol binario coloreado son más rápidas en comparación con los árboles B porque los árboles coloreados no intentan maximizar el factor de relleno de cada grupo horizontal de nodos (solo se garantiza el factor de relleno mínimo en árboles binarios coloreados, limitando el número de divisiones o uniones de grupos). Los árboles B serán más rápidos para realizar rotaciones (porque las rotaciones ocurrirán con frecuencia dentro del mismo grupo en lugar de múltiples nodos separados en un árbol binario coloreado). Sin embargo, para almacenar grandes volúmenes, los árboles B serán mucho más rápidos ya que serán más compactos al agrupar a varios elementos secundarios en el mismo grupo donde se puede acceder a ellos localmente.
Todas las optimizaciones posibles en los árboles B para aumentar los factores de relleno promedio de los clústeres son posibles en el árbol binario multicolor equivalente. En particular, maximizar el factor de relleno promedio en un árbol B estructuralmente equivalente es lo mismo que reducir la altura total del árbol multicolor, aumentando el número de nodos que no son negros. El peor caso ocurre cuando todos los nodos en un árbol binario coloreado son negros, el mejor caso ocurre cuando solo un tercio de ellos son negros (y los otros dos tercios son nodos rojos).
Aplicaciones y estructuras de datos relacionadas
Los árboles rojo-negro ofrecen garantías en el peor de los casos para el tiempo de inserción, el tiempo de eliminación y el tiempo de búsqueda. Esto no solo los hace valiosos en aplicaciones sensibles al tiempo, como las aplicaciones en tiempo real, sino que los convierte en bloques de construcción valiosos en otras estructuras de datos que brindan garantías en el peor de los casos; por ejemplo, muchas estructuras de datos utilizadas en la geometría computacional pueden basarse en árboles rojo-negro, y el programador completamente justo utilizado en los kernels de Linux actuales y la implementación de llamadas al sistema epoll utiliza árboles rojo-negro.
El árbol AVL es otra estructura que apoya O()log n){displaystyle O(log n)} búsqueda, inserción y eliminación. Los árboles AVL pueden ser de color rojo-negro, por lo tanto son un subconjunto de árboles RB. La peor altura es 0.720 veces la peor altura de los árboles RB, por lo que los árboles AVL son más rígidamente equilibrados. Las mediciones de rendimiento de Ben Pfaff con casos de prueba realistas en 79 carreras encuentran ratios AVL a RB entre 0.677 y 1.077, mediana a 0.947 y media geométrica 0.910. Los árboles WAVL tienen un rendimiento entre esos dos.
Los árboles rojo-negro también son particularmente valiosos en la programación funcional, donde son una de las estructuras de datos persistentes más comunes, utilizadas para construir arrays y conjuntos asociativos que pueden retener versiones anteriores después de mutaciones. La versión persistente de los árboles rojo-negro requiere O()log n){displaystyle O(log n)} espacio para cada inserción o eliminación, además del tiempo.
Por cada 2 a 4 árboles, hay árboles rojos y negros correspondientes con elementos de datos en el mismo orden. Las operaciones de inserción y eliminación en 2 a 4 árboles también son equivalentes al cambio de color y las rotaciones en árboles rojo-negro. Esto hace que 2 a 4 árboles sean una herramienta importante para comprender la lógica detrás de los árboles rojo-negro, y es por eso que muchos textos introductorios de algoritmos presentan 2 a 4 árboles justo antes de los árboles rojo-negro, aunque 2 a 4 árboles no se usan a menudo en práctica.
En 2008, Sedgewick introdujo una versión más simple del árbol rojo-negro llamado árbol rojo-negro inclinado a la izquierda mediante la eliminación de un grado de libertad no especificado previamente en la implementación. El LLRB mantiene una invariante adicional de que todos los enlaces rojos deben inclinarse hacia la izquierda, excepto durante las inserciones y eliminaciones. Los árboles rojo-negro se pueden hacer isométricos para 2 o 3 árboles o para 2 o 4 árboles, para cualquier secuencia de operaciones. La isometría de 2 a 4 árboles fue descrita en 1978 por Sedgewick. Con 2 a 4 árboles, la isometría se resuelve con un "cambio de color" correspondiente a una división, en la que el color rojo de dos nodos secundarios deja a los secundarios y se traslada al nodo principal.
La descripción original del árbol de tango, un tipo de árbol optimizado para búsquedas rápidas, usa específicamente árboles rojo-negro como parte de su estructura de datos.
A partir de Java 8, el HashMap ha sido modificado de tal manera que en lugar de utilizar un LinkedList para almacenar diferentes elementos con hashcodes colliding, se utiliza un árbol rojo-negro. Esto da lugar a la mejora de la complejidad del tiempo de búsqueda de tal elemento O()m){displaystyle O(m)} a O()log m){displaystyle O(log m)} Donde m{displaystyle m} es el número de elementos con hashcodes colliding.
Operaciones
Las operaciones de sólo lectura, como búsqueda o traversal de árboles, en un árbol rojo-negro no requieren ninguna modificación de los utilizados para buscar árboles binarios, porque cada árbol rojo-negro es un caso especial de un simple árbol de búsqueda binaria. Sin embargo, el resultado inmediato de una inserción o eliminación puede violar las propiedades de un árbol rojo-negro, cuya restauración se llama rebalancing para que los árboles rojo-negro se vuelvan auto-balancing. Requiere en el peor caso un pequeño número, O()log n){displaystyle O(log n)} en Big O notation, donde n{displaystyle n} es el número de objetos en el árbol, en promedio o amortizado O()1){displaystyle O(1)}, un número constante, de cambios de color (que son muy rápidos en la práctica); y no más de tres rotaciones de árboles (dos para la inserción).
Si la implementación de ejemplo a continuación no es adecuada, se pueden encontrar otras implementaciones con explicaciones en la biblioteca C anotada GNU libavl de Ben Pfaff (v2.0.3 a partir de junio de 2019).
Los detalles de las operaciones de inserción y eliminación se demostrarán con código C++ de ejemplo. El código de ejemplo utiliza las definiciones de tipo y las macros siguientes, así como la función auxiliar para las rotaciones:
// Definiciones básicas de tipo:enum color_t {} BLACK, RED };struct RBnode {} // nodo de árbol rojo-negro RBnode* padre; // == NIL si raíz del árbol RBnode* niño[2]; // == NIL si el niño está vacío // El índice es: // LEFT:= 0, si (llamado) // DERECHO:= 1, si enum color_t color; int clave;};#define NIL NULL // null pointer or pointer to sentinel node#define LEFT 0#Define Right 1#define left child[LEFT]#define right child[RIGHT]struct RBtree {} / Árbol rojo-negro RBnode* root; // == NIL si el árbol está vacío};// Obtener la dirección del niño (izquierda { izquierda, derecha)// of the non-root non-NIL RBnode* N:#define childDir(N) (N == (N- Conféroe)- correctamente ? Derecha: izquierda)RBnode* RotateDirRoot() RBtree* T, / Árbol rojo-negro RBnode* P, // root de subtree ()podrá Ser el root de T) int dir) {} // dir latitud { izquierda, derecha } RBnode* G = P-padre; RBnode* S = P-niño[1-dir]; RBnode* C; afirmación()S ! NIL); // puntero a verdadero nodo requerido C = S-niño[dir]; P-niño[1-dir] = C; si ()C ! NIL) C-padre = P; S-niño[ dir] = P; P-padre = S; S-padre = G; si ()G ! NULL) G-niño[ P == G-derecho ? Bien. : LEFT ] = S; más T-root = S; retorno S; // nueva raíz del subárbol}#define RotateDir(N,dir) RotateDirRoot(T,N,dir)#define RotateLeft(N) RotateDirRoot(T,N,LEFT)#define RotateRight(N) RotateDirRoot(T,N,RIGHT)
Notas al código de muestra y diagramas de inserción y extracción
La propuesta desglosa tanto la inserción como la remoción (sin mencionar algunos casos muy simples), en seis constelaciones de nodos, aristas y colores, que se denominan casos. La propuesta contiene tanto para la inserción como para la eliminación, exactamente un caso que avanza un nivel de negro más cerca de la raíz y los bucles, los otros cinco casos reequilibran el árbol propio. Los casos más complicados se representan en un diagrama.
- La variable
Ndenota el nodo actual, que se etiqueta N en los diagramas.  simboliza un nodo rojo y
simboliza un nodo rojo y  a (no NNL) nodo negro (de altura negra ≥ 1),
a (no NNL) nodo negro (de altura negra ≥ 1),  simboliza el color rojo o negro de un nodo no-NIL, pero el mismo color a lo largo del mismo diagrama. Los nodos NIL no están representados en los diagramas.
simboliza el color rojo o negro de un nodo no-NIL, pero el mismo color a lo largo del mismo diagrama. Los nodos NIL no están representados en los diagramas.- Un diagrama contiene tres columnas y dos a cuatro acciones. La columna izquierda muestra la primera iteración, la columna derecha las iteraciones superiores, la columna media muestra la segmentación de un caso en sus diferentes acciones.
- La acción "entrada" muestra la constelación de nodos con sus colores que define un caso y en su mayoría viola algunos de los requisitos.
Una frontera azul suena el nodo actual N y los otros nodos son etiquetados según su relación con N. - Si una rotación es considerada útil, esto se muestra en la siguiente acción, que se etiqueta "rotación".
- Si algunos recolorantes se consideran útiles, esto se imagina en la siguiente acción, que se etiqueta "color".
- Si todavía hay alguna necesidad de reparar, los casos hacen uso del código de otros casos y esto después de una reasignación del nodo actual N, que de nuevo lleva un anillo azul y relativo a lo que otros nodos pueden tener que ser reasignados también. Esta acción es etiquetada "reassign".
Para ambos, insertar y eliminar, hay (exactamente) un caso que itera un nivel negro más cerca de la raíz; entonces la constelación reasignada satisface el loop respectivo invariante.
- Un triángulo posiblemente numerado con un círculo negro encima
 representa un subárbol rojo-negro (conectado a su padre según el requisito 3) con una altura negra igual al nivel de iteración menos uno, es decir, cero en la primera iteración. Su raíz puede ser roja o negra.
representa un subárbol rojo-negro (conectado a su padre según el requisito 3) con una altura negra igual al nivel de iteración menos uno, es decir, cero en la primera iteración. Su raíz puede ser roja o negra.
Un triángulo posiblemente numerado representa un subárbol rojo-negro con una altura negra uno menos, es decir, su padre tiene la altura negra cero en la segunda iteración.
representa un subárbol rojo-negro con una altura negra uno menos, es decir, su padre tiene la altura negra cero en la segunda iteración.
- Remark
- Para la simplicidad, el código muestral utiliza la disyunción:
U == NIL || U->color == BLACK // considered black
- y la conjunción:
U != NIL && U->color == RED // not considered black
- Por tanto, hay que tener en cuenta que ambas declaraciones son no evaluado en total, si
U == NIL. Entonces en ambos casosU->colorno se toca (ver evaluación de cortocircuito).
(El comentario)considered blackde conformidad con el requisito 2.) - Los relacionados
if- las declaraciones tienen que ocurrir con mucha menos frecuencia si se realiza la propuesta.
Inserción
La inserción comienza colocando el nuevo nodo (no NIL), digamos N, en la posición en el árbol de búsqueda binaria de un nodo NIL cuya clave del predecesor en orden se compara menos que la del nuevo nodo clave, que a su vez se compara menos que la clave de su sucesor en orden.
(Con frecuencia, este posicionamiento es el resultado de una búsqueda dentro del árbol que precede inmediatamente a la operación de inserción y consiste en un nodo P junto con una dirección dir con P->child[dir] == NIL.)
El nodo recién insertado se colorea temporalmente de rojo para que todas las rutas contengan la misma cantidad de nodos negros que antes.
Pero si su padre, digamos P, también es rojo, entonces esta acción introduce una infracción roja.
vacío RBinsert1() RBtree* T, // Árbol rojo-negro struct RBnode* N, // nodo a insertar struct RBnode* P, // - padre nodos de N () podrá Ser NULL ) byte dir) // lado (LEFT o DERECHO) de P donde insertar N{} struct RBnode* G; // - Nodo padre de P struct RBnode* U; // tío de N N-color = RED; N-izquierda = NIL; N-derecho = NIL; N-padre = P; si ()P == NULL) {} // No hay padre T-root = N; // N es la nueva raíz del árbol T. retorno; // inserción completa } P-niño[dir] = N; // insertar N como dir-child of P // inicio del (hacer mientras)-loop: do {}El ciclo de reequilibrio de la operación de inserción tiene el siguiente invariante:
- El nodo actual N es
 (rojo) al principio de cada iteración.
(rojo) al principio de cada iteración. - Requisito 3 está satisfecho para todos los pares node←parente con la posible excepción N←P cuando P es también rojo (una violación roja en N).
- Todas las demás propiedades (incluido el requisito 4) están satisfechas en todo el árbol.
Notas a los diagramas de inserción
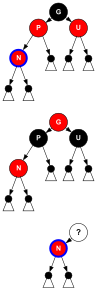
- En los diagramas, P se utiliza para N’s parent, G para el abuelo, y U will denote NEl tío.
- Los diagramas muestran el nodo padre P como hijo izquierdo de su padre G aunque sea posible P para estar de cualquier lado. El código muestral cubre ambas posibilidades por medio de la variable lateral
dir. - N es el nodo de inserción, pero a medida que la operación procede también otros nodos pueden volverse actuales (véase el caso I2).
- Los diagramas muestran los casos donde P es rojo también, la violencia roja.
- La columna x indica el cambio en la dirección del niño, es decir, o (para "extra") significa que P y N son los niños izquierdos o ambos derecho, mientras que yo (para "inner") significa que la dirección del niño cambia de P’s to N’s.
- El grupo de la columna antes define el caso, cuyo nombre se da en la columna Caso. Por tanto, se ignoran los posibles valores en las células vacías. Así que en el caso I2 el código de muestra cubre ambas posibilidades de direcciones infantiles de N, aunque el diagrama correspondiente muestra sólo uno.
- Las filas en la sinopsis se ordenan de tal manera que la cobertura de todos los casos RB posibles es fácilmente comprensible.
- La columna rotación indica si una rotación contribuye a la reducción.
- La columna asignación muestra una asignación de N antes de entrar en un paso posterior. Esto posiblemente induzca una reasignación de los otros nodos P, G, U también.
- Si algo ha sido cambiado por el caso, esto se muestra en el grupo de columna después.
- Una flecha → en la columna siguiente significa que el reequilibrio está completo con este paso. Si la columna después determina exactamente un caso, este caso se da como el posterior, de lo contrario hay marcas de preguntas.
- El bucle está contenido en las secciones "Insert case I1" y "Insert case I2", donde en caso de I2 el problema de rebalamentación se intensifica Δ Δ h=2{displaystyle Delta h=2} niveles más altos en el árbol, en que el abuelo G se convierte en el nuevo nodo actual N. Así que se necesita al máximo h2{displaystyle {tfrac {h}{2}} pasos de la iteración para reparar el árbol (donde h{displaystyle h} es la altura del árbol). Debido a que la probabilidad de escalada disminuye exponencialmente con cada paso el coste total de reequilibrio es constante en promedio, de hecho amortizado constante.
- Desde el cuerpo del bucle, el caso I1 sale por sí mismo y hay ramas de salida a los casos I4, I6, I5 + I6, e I3.
- Las rotaciones ocurren en casos I6 y I5 + I6 – fuera del bucle. Por lo tanto, en la mayoría de dos rotaciones se producen en total.
Insertar caso I1
El padre P del nodo actual es negro, por lo que se cumple el requisito 3. El requisito 4 también se cumple de acuerdo con el bucle invariante.
si ()P-color == BLACK) {} // Case_I1 (P negro): retorno; // inserción completa } // A partir de ahora P es rojo. si ()G = P-padre) == NULL) Goto Case_I4; // P rojo y raíz // si no: P rojo y G!=NULL. dir = niño Dir()P); // el lado del padre G en el que se encuentra el nodo P U = G-niño[1-dir]; // tío si ()U == NIL Silencio U-color == BLACK) // considerado negro Goto Case_I56; / P rojo " U negroInsertar caso I2
Si tanto el padre P como el tío U son rojos, ambos se pueden volver a pintar de negro y el abuelo G se vuelve rojo para mantener el requisito 4. Dado que cualquier camino a través del padre o tío debe pasar por el abuelo, la cantidad de nodos negros en estos caminos no ha cambiado. Sin embargo, el abuelo G ahora puede violar el requisito 3, si tiene un padre rojo. Después de volver a etiquetar G a N, el ciclo invariante se cumple para que el reequilibrio se pueda iterar en un nivel negro (= 2 niveles de árbol) más alto.
// Case_I2 (P+U rojo): P-color = BLACK; U-color = BLACK; G-color = RED; N = G; // nuevo nodo actual // iterate 1 nivel negro superior // (= 2 niveles de árboles) } mientras ()P = N-padre) ! NULL); // final del (do while)-loopInsertar caso I3
Insert case I2 has been executed for h− − 12{fnMicroc} {h-1}{2}} tiempos y la altura total del árbol ha aumentado en 1, ahora siendo h.{displaystyle H~.El nodo actual N es la raíz (rojo) del árbol, y todas las propiedades RB están satisfechas.
// Dejar el (hacer mientras)-loop (después de haber caído de Case_I2). // Case_I3: N es la raíz y el rojo. retorno; // inserción completaInsertar caso I4
El padre P es rojo y la raíz. Como N también es rojo, se infringe el requisito 3. Pero después de cambiar el color de P, el árbol tiene forma de RB. La altura negra del árbol aumenta en 1.
Case_I4: // P es la raíz y el rojo: P-color = BLACK; retorno; // inserción completaInsertar caso I5
El padre P es rojo pero el tío U es negro. El objetivo final es rotar el nodo padre P a la posición principal, pero esto no funcionará si N es un nodo "interno" nieto de G (es decir, si N es el hijo izquierdo del hijo derecho de G o el hijo derecho del hijo izquierdo de G). Una dir-rotation en P cambia los roles del nodo actual N y su padre P. La rotación agrega caminos a través de N (aquellos en el subárbol etiquetado como 2, vea el diagrama) y elimina caminos a través de P (aquellos en el subárbol etiquetado como 4). Pero tanto P como N son rojos, por lo que se conserva el requisito 4. El requisito 3 se restablece en el caso 6.
Case_I56: // P red " U black: si ()N == P-niño[1-dir]) {} // Case_I5 (P red " U black " N interior grandchild of G): RotateDir()P,dir); // P nunca es la raíz N = P; // nuevo nodo actual P = G-niño[dir]; // nuevo padre de N // caer a Case_I6 }Insertar caso I6
Ahora es seguro que el nodo actual N será un "externo" nieto de G (a la izquierda del hijo izquierdo o a la derecha del hijo derecho). Ahora (1-dir)-rotate en G, poniendo P en lugar de G y haciendo P el padre de N y G. G es negro y su antiguo hijo P es rojo, ya que se violó el requisito 3. Después de cambiar los colores de P y G, el árbol resultante satisface el requisito 3. El requisito 4 también se cumple, ya que todos los caminos que pasaron por la G Ahora pasa por la P negra.
// Case_I6 (P red " U black " N outer grandchild of G): RotateDirRoot()T,G,1-dir); // G puede ser la raíz P-color = BLACK; G-color = RED; retorno; // inserción completa} // final de RBinsert1Debido a que el algoritmo transforma la entrada sin usar una estructura de datos auxiliar y usando solo una pequeña cantidad de espacio de almacenamiento adicional para las variables auxiliares, está en su lugar.
Eliminación: casos simples
La etiqueta N indica el nodo actual que en la entrada es el nodo que se eliminará.
Si N es la raíz que no tiene un hijo que no sea NIL, se reemplaza por un nodo NIL, después de lo cual el árbol está vacío y en forma de RB.
Si N tiene exactamente un hijo que no es NIL, debe ser un hijo rojo, porque si fuera negro, el requisito 4 obligaría a un segundo hijo negro que no es NIL.
Si N es un nodo rojo, no puede tener un hijo que no sea NIL, porque tendría que ser negro según el requisito 3. Además, no puede tener exactamente un hijo negro como se argumentó anteriormente. Como consecuencia, el nodo rojo N no tiene ningún hijo y simplemente se puede eliminar.
Si N es un nodo negro, puede tener un hijo rojo o ningún hijo que no sea NIL. Si N tiene un niño rojo, simplemente se reemplaza con este niño después de pintar este último de negro.
Remoción de una hoja negra sin raíces
Si N tiene dos niños no pertenecientes al NNL, una navegación adicional al elemento mínimo en su subárbol derecho (que es N’s in-order sucesor, decir Sí.{displaystyle {text{y}}}) encuentra un nodo sin otro nodo entre N y Sí.{displaystyle {text{y}}} (como se muestra aquí). Este nodo Sí.{displaystyle {text{y}}} tiene – como elemento mínimo de un subárbol – en la mayoría de un niño no-NIL. Si Sí.{displaystyle {text{y}}} debe ser eliminado N’s lugar, los datos del árbol rojo-negro relacionados con N y Sí.{displaystyle {text{y}}}, es decir, el color y los punteros a y desde los dos nodos, tienen que ser intercambiados. (Como resultado, el árbol rojo-negro modificado es el mismo que antes, excepto que el orden entre N y Sí.{displaystyle {text{y}}} se invierte.) Esta elección puede dar lugar a uno de los casos más simples anteriores, pero si Sí.{displaystyle {text{y}}} es sin niño y negro llegamos a...
El caso complejo es cuando N no es la raíz, es de color negro y no tiene un hijo propio (⇔ solo hijos NIL). En la primera iteración, N se reemplaza por NIL.
vacío RBdelete2() RBtree* T, // Árbol rojo-negro struct RBnode* N) // nodo por eliminar {} struct RBnode* P = N-padre; // - Nodo padre de N byte dir; // lado de P en el que N se encuentra (puerto { LEFT, DERECHO }) struct RBnode* S; // hermano de N struct RBnode* C; // sobrino cercano struct RBnode* D; // sobrino lejano // P= NULL, ya que N no es la raíz. dir = niño Dir()N); // lado del padre P en el que se encuentra el nodo N // Reemplazar N a su padre P por NIL: P-niño[dir] = NIL; Goto Start_D; // salto en el bucle // inicio del (hacer mientras)-loop: do {} dir = niño Dir()N); // lado del padre P en el que se encuentra el nodo NStart_D: S = P-niño[1-dir]; / / / hermano de N (tiene la altura negra 1) D = S-niño[1-dir]; // sobrino lejano C = S-niño[ dir]; // cercano sobrino si ()S-color == RED) Goto Case_D3; / S red === P+C+D negro // S es negro: si ()D ! NIL " D-color == RED) // no considerado negro Goto Case_D6; / D rojo " S negro si ()C ! NIL " C-color == RED) // no considerado negro Goto Case_D5; // C red " S+D negro // Aquí ambos sobrinos son == NIL (primera iteración) o negro (más tarde). si ()P-color == RED) Goto Case_D4; // P rojo " C+S+D negroEl ciclo de reequilibrio de la operación de eliminación tiene el siguiente invariante:
- Al principio de cada iteración la altura negra de N iguala el número de iteración menos uno, lo que significa que en la primera iteración es cero y que N es un verdadero nodo negro
 en iteraciones más altas.
en iteraciones más altas. - El número de nodos negros en los caminos a través de N es uno menos que antes de la eliminación, mientras que no se cambia en todos los otros caminos, por lo que hay una violación negra en P si existen otros caminos.
- Todas las demás propiedades (incluyendo el requisito 3) están satisfechas en todo el árbol.
Notas a los diagramas de borrado
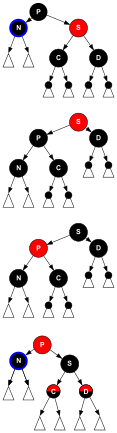
- En los diagramas de abajo, P se utiliza para N’s parent, S para el hermano de N, C (que significa) cerca sobrino) S’s niño en la misma dirección N, y D (que significa) distante sobrino) S’s otro niño (S no puede ser un nodo NIL en la primera iteración, porque tiene que tener la altura negra uno, que era la altura negra de N antes de su eliminación, pero C y D puede ser NIL nodos).
- Los diagramas muestran el nodo actual N como hijo izquierdo de su padre P aunque sea posible N para estar de cualquier lado. Las muestras de código cubren ambas posibilidades por medio de la variable lateral
dir. - Al principio (en la primera iteración) de la remoción, N es el nodo NIL que reemplaza el nodo para ser eliminado. Debido a que su ubicación en el nodo de los padres es la única cosa de importancia, se simboliza por
 (que significa: el nodo actual N es un nodo NIL y un niño izquierdo) en la columna izquierda de los diagramas de eliminación. A medida que la operación procede también los nodos adecuados (de altura negra ≥ 1) pueden volverse actuales (véase por ejemplo el caso D2).
(que significa: el nodo actual N es un nodo NIL y un niño izquierdo) en la columna izquierda de los diagramas de eliminación. A medida que la operación procede también los nodos adecuados (de altura negra ≥ 1) pueden volverse actuales (véase por ejemplo el caso D2). - Contando las balas negras (
 y
y  ) en un diagrama de borrado se puede observar que los caminos a través de N tienen una bala menos que los otros caminos. Esto significa una violación negra P- si existe.
) en un diagrama de borrado se puede observar que los caminos a través de N tienen una bala menos que los otros caminos. Esto significa una violación negra P- si existe. - La constelación de color en grupo de columna antes define el caso, cuyo nombre se da en la columna Caso. Por tanto, se ignoran los posibles valores en las células vacías.
- Las filas en la sinopsis se ordenan de tal manera que la cobertura de todos los casos RB posibles es fácilmente comprensible.
- La columna rotación indica si una rotación contribuye a la reducción.
- La columna asignación muestra una asignación de N antes de entrar en un paso posterior de la iteración. Esto posiblemente induzca una reasignación de los otros nodos P, C, S, D también.
- Si algo ha sido cambiado por el caso, esto se muestra en el grupo de columna después.
- Una flecha → en la columna siguiente significa que el reequilibrio está completo con este paso. Si la columna después determina exactamente un caso, este caso se da como el posterior, de lo contrario hay marcas de preguntas.
- El bucle está contenido en las secciones de
Start_Da través de "Delete case D2", donde el problema de la reducción se intensifica Δ Δ h=1{displaystyle Delta h=1} nivel superior en el árbol en que el padre P se convierte en el nuevo nodo actual N. Así que se necesita al máximo h{displaystyle h} iteraciones para reparar el árbol (donde h{displaystyle h} es la altura del árbol). Debido a que la probabilidad de escalada disminuye exponencialmente con cada iteración el coste total de reequilibración es constante en promedio, de hecho amortizado constante. (Al igual que un lado: Mehlhorn & Sanders señalan: "Los árboles AVL sí no soporte constante costos de actualización amortizados." Esto es cierto para el reequilibrio después de una eliminación, pero no la inserción AVL.) - Fuera del cuerpo del bucle hay ramas de salida a los casos D3, D6, D5 + D6, D4, y D1; sección "Caso completo D3" por su cuenta tiene tres ramas de salida diferentes a los casos D6, D5 y D4.
- Las rotaciones ocurren en casos D6 y D5 + D6 y D3 + D5 + D6 - todo fuera del bucle. Por lo tanto, en la mayoría de tres rotaciones se producen en total.
Eliminar caso D1
El nodo actual N es la nueva raíz. Se eliminó un nodo negro de cada ruta, por lo que se conservan las propiedades RB. La altura negra del árbol disminuye en 1.
// Case_D1 (P == NULL): retorno; // Eliminación completaEliminar caso D2
Los hijos deP, S y S son negros. Después de pintar S rojo todos los caminos que pasan por S, que son precisamente los caminos no que pasan por N, tenga uno menos nodo negro. Ahora todos los caminos en el subárbol cuya raíz es P tienen la misma cantidad de nodos negros, pero uno menos que los caminos que no pasan por P, por lo que el requisito 4 aún puede ser violado Después de volver a etiquetar P a N, la invariante del ciclo se cumple para que el reequilibrio se pueda iterar en un nivel negro (= 1 nivel de árbol) más alto.
// Case_D2 (P+C+S+D negro): S-color = RED; N = P; // nuevo nodo actual (tal vez la raíz) // iterate 1 nivel negro // (= 1 nivel de árbol) superior } mientras ()P = N-padre) ! NULL); // final del (do while)-loopEliminar caso D3
El hermano S es rojo, entonces P y los sobrinos C y D tienen que ser negros. Una dir-rotation en P convierte S en N el abuelo de
Luego, después de invertir los colores de P y S, el camino a través de N aún es corto en un nodo negro. Pero N tiene un padre rojo P y un hermano negro S, por lo que las transformaciones en los casos D4, D5 o D6 pueden restaurar el forma RB.
Case_D3: // S red " P+C+D negro: RotateDirRoot()T,P,dir); // P puede ser la raíz P-color = RED; S-color = BLACK; S = C; //= NIL // now: P red " S black D = S-niño[1-dir]; // sobrino lejano si ()D ! NIL " D-color == RED) Goto Case_D6; / D rojo " S negro C = S-niño[ dir]; // cercano sobrino si ()C ! NIL " C-color == RED) Goto Case_D5; // C red " S+D negro // De lo contrario C+D considerado negro. // caer a Case_D4Eliminar caso D4
Los hijos del hermano S y S son negros, pero P es rojo. El intercambio de los colores de S y P no afecta la cantidad de nodos negros en las rutas que pasan por S, pero agrega uno al número de nodos negros en caminos que pasan por N, compensando el nodo negro eliminado en esos caminos.
Case_D4: // P rojo " S+C+D negro: S-color = RED; P-color = BLACK; retorno; // Eliminación completaEliminar caso D5
El hermano S es negro, S’s close child C es rojo, y S’s distant child D es negro. Después de un (1-dir)- rotación a S el sobrino C se convierte en S’s parent and N’s nuevo hermano. Los colores de S y C son intercambiados.
Todos los caminos todavía tienen el mismo número de nodos negros, pero ahora N tiene un hermano negro cuyo hijo lejano es rojo, por lo que la constelación es adecuada para el caso D6. Ni tampoco N ni su padre P son afectados por esta transformación, y P puede ser rojo o negro (![]() en el diagrama).
en el diagrama).
Case_D5: // C rojo " S+D negro: RotateDir()S,1-dir); // S nunca es la raíz S-color = RED; C-color = BLACK; D = S; S = C; // now: D red " S black // caer a Case_D6Eliminar caso D6
El hermano S es negro, S’s distant child D es rojo. Después de un dir- rotación a P el hermano S se convierte en el padre de P y S’s distant child D. Los colores de P y S son intercambiados, y D está hecho negro. El subárbol todavía tiene el mismo color en su raíz, es decir, rojo o negro (![]() en el diagrama), que se refiere al mismo color tanto antes como después de la transformación. De esta manera se conserva el requisito 3. Los caminos en el subárbol no pasan por N (i.o.w. paseando D and node 3 en el diagrama) pasar por el mismo número de nodos negros que antes, pero N ahora tiene un ancestro negro adicional: P se ha vuelto negro, o era negro y S fue añadido como un abuelo negro. Así, los caminos que pasan por N pasar a través de un nodo negro adicional, por lo que el requisito 4 es restaurado y el árbol total está en forma RB.
en el diagrama), que se refiere al mismo color tanto antes como después de la transformación. De esta manera se conserva el requisito 3. Los caminos en el subárbol no pasan por N (i.o.w. paseando D and node 3 en el diagrama) pasar por el mismo número de nodos negros que antes, pero N ahora tiene un ancestro negro adicional: P se ha vuelto negro, o era negro y S fue añadido como un abuelo negro. Así, los caminos que pasan por N pasar a través de un nodo negro adicional, por lo que el requisito 4 es restaurado y el árbol total está en forma RB.
Case_D6: // D red " S black: RotateDirRoot()T,P,dir); // P puede ser la raíz S-color = P-color; P-color = BLACK; D-color = BLACK; retorno; // Eliminación completa} // final de RBdelete2Debido a que el algoritmo transforma la entrada sin usar una estructura de datos auxiliar y usando solo una pequeña cantidad de espacio de almacenamiento adicional para las variables auxiliares, está en su lugar.
Prueba de límites
Para h▪ ▪ N{displaystyle hin mathbb {N} hay un árbol rojo-negro de la altura h{displaystyle h} con
mh=2⌊ ⌊ ()h+1)/2⌋ ⌋ +2⌊ ⌊ h/2⌋ ⌋ − − 2={}2⋅ ⋅ 2h2− − 2=2h2+1− − 23⋅ ⋅ 2h− − 12− − 2{displaystyle {begin{ll}m_{h} limit=2^{lfloor (h+1)/2rfloor }+2^{lfloor h/2rfloor 2\\\\begin{cases}2cdot 2^{tfrac {h}{2}-2=2^{tfrac} {h}{2}+1}-23cdot 2^{tfrac {h-1}{2}-2end{cases}}end{array}} (con función de suelo) ⌊ ⌊ ⌋ ⌋ {displaystyle lfloor ,rfloor }) si h{displaystyle h} incluso si h{displaystyle h} extraño
nodos y no hay un árbol rojo-negro de esta altura del árbol con menos nodos – por lo tanto es mínimo.
Su altura negra es ⌈ ⌈ h/2⌉ ⌉ {displaystyle lceil h/2rceil } (con raíz negra) o para extraño h{displaystyle h} (entonces con una raíz roja) también ()h− − 1)/2.{displaystyle (h-1)/2~.}
- Prueba
Para que un árbol rojo-negro de cierta altura tenga una cantidad mínima de nodos, debe tener exactamente una ruta más larga con la cantidad máxima de nodos rojos, para lograr una altura de árbol máxima con una altura negra mínima. Además de este camino, todos los demás nodos deben ser negros. Si se quita un nodo de este árbol, pierde altura o alguna propiedad de RB.
El árbol RB de altura h=1{displaystyle h=1} con raíz roja es mínima. Esto está de acuerdo con
- m1=2⌊ ⌊ ()1+1)/2⌋ ⌋ +2⌊ ⌊ 1/2⌋ ⌋ − − 2=21+20− − 2=1.{displaystyle m_{1}=2^{lfloor (1+1)/2rfloor }!+!2^{lfloor 1/2rfloor }! 2=2^{1}!+!2^{0}!!
Un árbol RB mínimo (RB)h en la figura 4) de la altura 1}" xmlns="http://www.w3.org/1998/Math/MathML">h■1{displaystyle h título1}1}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/3df33213a54649226c03c8115b130c49170d0683" style="vertical-align: -0.338ex; width:5.6ex; height:2.176ex;"/> tiene una raíz cuyos dos subárboles infantiles son de diferente altura. El subárbol infantil superior es también un árbol de RB mínimo, RBh–1, que contiene también un camino más largo que define su altura h− − 1{displaystyle h!; tiene mh− − 1{displaystyle M_{h-1} nodos y la altura negra ⌊ ⌊ ()h− − 1)/2⌋ ⌋ =s.{displaystyle lfloor (h!!!1)/2rfloor =:s.} El otro subárbol es un árbol binario perfecto de altura (negro) s{displaystyle s} teniendo 2s− − 1=2⌊ ⌊ ()h− − 1)/2⌋ ⌋ − − 1{displaystyle 2^{s}!!!!1=2^{lfloor (h-1)/2rfloor }! Nodos negros, y ningún nodo rojo. Entonces el número de nodos es por inducción
| mh{displaystyle m_{h} | ={displaystyle =} | ()mh− − 1){displaystyle (m_{h-1})} | +{displaystyle +} | ()1){displaystyle (1)} | +{displaystyle +} | ()2⌊ ⌊ ()h− − 1)/2⌋ ⌋ − − 1){displaystyle (2^{lfloor (h-1)/2rfloor }-1)} | ||||
| (Subtree más alto) | (root) | (segundo subárbol) | ||||||||
| resultantes | ||||||||||
| mh{displaystyle m_{h} | ={displaystyle =} | ()2⌊ ⌊ h/2⌋ ⌋ +2⌊ ⌊ ()h− − 1)/2⌋ ⌋ − − 2){displaystyle (2^{lfloor h/2rfloor }+2^{lfloor (h-1)/2rfloor }-2)} | +{displaystyle +} | 2⌊ ⌊ ()h− − 1)/2⌋ ⌋ {displaystyle 2^{lfloor (h-1)/2rfloor } | ||||||
| ={displaystyle =} | 2⌊ ⌊ h/2⌋ ⌋ +2⌊ ⌊ ()h+1)/2⌋ ⌋ − − 2{displaystyle 2^{lfloor h/2rfloor }+2^{lfloor (h+1)/2rfloor }-2}■ | |||||||||
El gráfico de la función mh{displaystyle m_{h} es convex y lineal a mano con puntos de rotura en ()h=2kSilenciom2k=2⋅ ⋅ 2k− − 2){displaystyle (h=2k; remain;m_{2k}=2cdot 2^{k}!-!2)} Donde k▪ ▪ N.{displaystyle kin mathbb {N} La función ha sido tabulada como mh={displaystyle # A027383(h–1) para h≥ ≥ 1{displaystyle hgeq 1} (secuencia) A027383 en el OEIS).
- Resolver la función para h{displaystyle h}
La desigualdad 8=2^{3}}" xmlns="http://www.w3.org/1998/Math/MathML">9■8=23{displaystyle 9 título8=2^{3}8=2^{3}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9fc6aa3b743ffc4de7d75d22ec4e30b93ae86037" style="vertical-align: -0.338ex; width:10.739ex; height:2.676ex;"/> conduce a 2^{3/2}}" xmlns="http://www.w3.org/1998/Math/MathML">3■23/2{displaystyle 3 títulos
2^{3/2}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/289041b8c90d373cd5129f1c257ef854de064e4c" style="vertical-align: -0.338ex; width:8.122ex; height:2.843ex;"/>, que por extraño h{displaystyle h} conduce a
- 2cdot 2^{h/2}-2}" xmlns="http://www.w3.org/1998/Math/MathML">mh=3⋅ ⋅ 2()h− − 1)/2− − 2=()3⋅ ⋅ 2− − 3/2)⋅ ⋅ 2()h+2)/2− − 2■2⋅ ⋅ 2h/2− − 2{displaystyle m_{h}=3cdot 2^{(h-1)/2}-2={bigl (}3cdot 2^{-3/2}{bigr)}cdot 2^{(h+2)/2}2cdot 2^{h/2}-2}
2cdot 2^{h/2}-2}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/11105813afbd3e754a837dae4eb53795fdf60696" style="vertical-align: -1.005ex; width:60.712ex; height:3.509ex;"/>.
Así que en el caso incluso tan extraño, h{displaystyle h} está en el intervalo
| log2 ()n+1){displaystyle log _{2}(n+1)} | ≤ ≤ h≤ ≤ {displaystyle leq hleq} | 2log2 ()n+2)− − 2=2log2 ()n/2+1){displaystyle 2log _{2}(n+2)-2=2log _{2}(n/2+1)} | <math alttext="{displaystyle {bigl [}[.2log2 ()n+1)]{displaystyle {bigl [}traducido2log _{2}(n+1);{bigr]}}<img alt="{displaystyle {bigl [} | |
| (Árbol binario perfecto) | (árbol rojo-negro mínimo) |
con n{displaystyle n} siendo el número de nodos.
- Conclusión
Un árbol rojo-negro con n{displaystyle n} nodos (keys) tiene altura de árbol h▪ ▪ O()log n).{displaystyle hin O(log n).}
Operaciones fijas y operaciones masivas
Además de las operaciones de inserción, eliminación y búsqueda de un solo elemento, se han definido varias operaciones de conjuntos en árboles rojo-negro: unión, intersección y diferencia de conjuntos. Luego, se pueden implementar operaciones masivas rápidas sobre inserciones o eliminaciones basadas en estas funciones establecidas. Estas operaciones de configuración se basan en dos operaciones auxiliares, Dividir y Unir. Con las nuevas operaciones, la implementación de árboles rojo-negro puede ser más eficiente y altamente paralelizable. Para lograr sus complejidades de tiempo, esta implementación requiere que la raíz pueda ser roja o negra, y que cada nodo almacene su propia altura negra.
- Únase: La función Únase está en dos árboles rojo-negro t1 y t2 y una llave k, donde t1. k. t2Todas las llaves t1 son menos que k, y todas las llaves en t2 son mayores que k. Devuelve un árbol que contiene todos los elementos en t1, t2 así como k.
- Si los dos árboles tienen la misma altura negra, Únase simplemente crea un nuevo nodo con subárbol izquierdo t1, root k y subárbol derecho t2. Si ambos t1 y t2 tienen raíz negra, set k para ser roja. De lo contrario k se pone negro.
- Si las alturas negras son desiguales, supongamos que t1 tiene mayor altura negra que t2 (el otro caso es simétrico). Únase sigue la columna derecha t1 hasta un nodo negro c, que se balancea con t2. En este punto un nuevo nodo con niño izquierdo c, root k (para ser rojo) y niño derecho t2 se crea para reemplazar c. El nuevo nodo puede invalidar el invariante rojo-negro porque a la mayoría de los tres nodos rojos pueden aparecer en una fila. Esto se puede fijar con una rotación doble. Si el doble problema rojo se propaga a la raíz, la raíz se establece entonces como negra, restaurando las propiedades. El costo de esta función es la diferencia de las alturas negras entre los dos árboles de entrada.
- Split: Para dividir un árbol rojo-negro en dos árboles más pequeños, los más pequeños que la llave x, y los más grandes que la clave x, primero dibujar un camino desde la raíz insertando x en el árbol rojo-negro. Después de esta inserción, todos los valores menos que x se encontrará en la izquierda del camino, y todos los valores mayores que x se encontrará a la derecha. Aplicando Únase, todos los subárboles del lado izquierdo se fusionan con las teclas en el camino como nodos intermedios de abajo a arriba para formar el árbol izquierdo, y la parte derecha es simétrica.
- Para algunas aplicaciones, Split también devuelve un valor booleano denotando si x aparece en el árbol. El costo de Split es O()log n),{displaystyle O(log n),} orden de la altura del árbol. Este algoritmo en realidad no tiene nada que ver con ninguna propiedad especial de un árbol rojo-negro, y puede ser utilizado en cualquier árbol con un Únase operación, como un árbol AVL.
El algoritmo de combinación es el siguiente:
función JoinRightRB(T)L, k, TR):
si (TL.color=negro) y (TL.blackHeight=TR.blackAltura:
retorno Nodo(T)L, pervertido, hecho,R)
T'=Node(T)L.left, lotL.key,TL.color objeto,joinRightRB(T)L.right,k,TR)
si (TL(T'right.color=T'.right.right.right.color=red):
T'.right.right.color=black;
retorno rotateLeft(T')
retorno T''[recte T'] */
función JoinLeftRB(T)L, k, TR):
/* simétrica para unirseRight RB */
función (T)L, k, TR):
si TL.blackHeight TR.blackAltura:
T'=joinRightRB(T)L,k,TR)
si (T'.color=red) y (T'right.color=red):
T'.color=negro
retorno T.
si TR.blackHeight TL.blackAltura:
/* simétrica */
si (TL.color=negro) y (TR.color=negro):
retorno Nodo(T)L, pervertido, hecho,R)
retorno Nodo(T)L, loco, negro, tR)
El algoritmo de división es el siguiente:
función split(T, k): si (T = nil) retorno (Nil, false, nil) si (k = T.key) retorno (T.left, true, T.right) si (k) (L',b,R') = split(T.left, k) retorno (L',b,join(R',T.key,T.right)) (L',b,R') = split(T.right, k) retorno (join(T.left,T.key,L'),b,T.right)
La unión de dos árboles rojo-negro t1 y t2 que representan conjuntos A y B, es un árbol rojo-negro t que representa A ∪ B. La siguiente función recursiva calcula esta unión:
función sindicato(t)1, t2): si t1 = nil retorno t2 si t2 = nil retorno t1(L1,b,R1)=split(t)1,t2.key) proc1=Empieza: TL=unión(L)1,t2.left) proc2=Empieza: TR=unión(R)1,t2.right) Esperad todos proc1,proc2 retorno (T)L, t2.key, TR)
Aquí, se supone que split devuelve dos árboles: uno que contiene las claves menos su clave de entrada, otro que contiene las claves mayores. (El algoritmo no es destructivo, pero también existe una versión destructiva en el lugar).
El algoritmo para intersección o diferencia es similar, pero requiere la rutina auxiliar Join2 que es igual a Join pero sin la tecla central. En función de las nuevas funciones de unión, intersección o diferencia, se puede insertar o eliminar una o varias claves en el árbol rojo-negro. Dado que Split llama a Join pero no se ocupa directamente de los criterios de equilibrio de los árboles rojo-negro, dicha implementación suele denominarse "basada en unión" implementación.
La complejidad de cada unión, intersección y diferencia es O()mlog ()nm+1)){displaystyle Oleft(mlog left({n over m}+1right)right)} para dos árboles rojo-negro de tamaños m{displaystyle m} y n()≥ ≥ m){displaystyle n(geq m)}. Esta complejidad es óptima en cuanto al número de comparaciones. Más importante aún, ya que las llamadas recursivas a la unión, intersección o diferencia son independientes entre sí, se pueden ejecutar en paralelo con una profundidad paralela O()log mlog n){displaystyle O(log mlog n)}. Cuando m=1{displaystyle m=1}, la implementación basada en la unión tiene el mismo gráfico acíclico dirigido computacional (DAG) como inserción y eliminación de un solo elemento si la raíz del árbol más grande se utiliza para dividir el árbol más pequeño.
Algoritmos paralelos
Los algoritmos paralelos para construir árboles rojo-negro de listas ordenadas de elementos pueden funcionar en tiempo constante o O()log log n){displaystyle O(log log n)} tiempo, dependiendo del modelo de computadora, si el número de procesadores disponibles es asintomáticamente proporcional al número n{displaystyle n} de los artículos en que n→ → JUEGO JUEGO {displaystyle nto infty }. También se conocen algoritmos paralelos de búsqueda rápida, inserción y eliminación.
Los algoritmos basados en combinaciones para árboles rojo-negro son paralelos para operaciones masivas, incluidas unión, intersección, construcción, filtro, reducción de mapas, etc.
Operaciones masivas paralelas
Las operaciones básicas como la inserción, la eliminación o la actualización se pueden paralelizar definiendo operaciones que procesen masas de múltiples elementos. También es posible procesar lotes con varias operaciones básicas, por ejemplo, los lotes pueden contener elementos para insertar y también elementos para eliminar del árbol.
Los algoritmos para operaciones a granel no son sólo aplicables al árbol rojo-negro, sino que también pueden adaptarse a otras estructuras de datos de secuencia ordenada, como el árbol 2–3, 2–3–4 y (a,b)-árbol. En los siguientes algoritmos diferentes para insertar a granel se explicará, pero los mismos algoritmos también se pueden aplicar a la eliminación y actualización. La inserción a granel es una operación que inserta cada elemento de una secuencia I{displaystyle Yo... en un árbol T{displaystyle T}.
Basado en unión
Este enfoque se puede aplicar a cada estructura de datos de secuencias ordenadas que apoye unas operaciones eficientes de unión y división. La idea general es dividir I{displaystyle Yo... y T{displaystyle T} en múltiples partes y realizar las inserciones en estas partes en paralelo.
- Primero el vracs I{displaystyle Yo... los elementos a insertar deben ser ordenados.
- Después de eso, el algoritmo se divide I{displaystyle Yo... en k▪ ▪ N+{displaystyle kin mathbb {N} partes .. I1,⋯ ⋯ ,Ik.. {displaystyle langle I_{1},cdotsI_{k}rangle } de casi igual tamaño.
- Siguiente el árbol T{displaystyle T} tiene que dividirse k{displaystyle k} partes .. T1,⋯ ⋯ ,Tk.. {displaystyle langle T_{1},cdotsT_{k}rangle } de una manera, así que para cada <math alttext="{displaystyle jin mathbb {N} ^{+}|,1leq jj▪ ▪ N+Silencio1≤ ≤ j.k{displaystyle jin mathbb {N} {fnMicrosoft Sans Serif} j)<img alt="{displaystyle jin mathbb {N} ^{+}|,1leq j siguientes restricciones:
- <math alttext="{displaystyle {text{last}}(I_{j})último()Ij).primero()Tj+1){displaystyle {text{last} {f}} {text{first}}(T_{j+1})}<img alt="{displaystyle {text{last}}(I_{j})
- <math alttext="{displaystyle {text{last}}(T_{j})último()Tj).primero()Ij+1){displaystyle {text{last}} {text{ first} {text{first} {f} {f}} {f}}}}}<img alt="{displaystyle {text{last}}(T_{j})
- Ahora el algoritmo inserta cada elemento de Ij{displaystyle I_{j} en Tj{displaystyle T_{j} secuencialmente. Este paso tiene que ser realizado para cada j{displaystyle j}, que se puede hacer hasta k{displaystyle k} procesadores en paralelo.
- Finalmente, los árboles resultantes se unirán para formar el resultado final de toda la operación.
Tenga en cuenta que en el Paso 3 las limitaciones para dividir I{displaystyle Yo... asegurar que en el Paso 5 los árboles se pueden unir de nuevo y la secuencia resultante se ordena.
El pseudocódigo muestra una implementación simple de divide y vencerás del algoritmo basado en combinaciones para la inserción masiva. Ambas llamadas recursivas se pueden ejecutar en paralelo. La operación de unión utilizada aquí difiere de la versión explicada en este artículo, en su lugar se utiliza join2, que pierde el segundo parámetro k.
Inserción(T, I, k): I.sort() volqueteInsertRec(T, I, k) gruesoInsertRec(T, I, k): si k = 1: para todos e dentro I: T.insert(e) másm:= ⌊size(I) / 2⌋ (T1, _, T2):= split(T, I[m]) gruesoInsertRec(T)1, I[0. m], ⌈k / 2⌉) TENIDO VOLVERInsertRec(T)2, I[m + 1.. tamaño(I) - 1], ⌊k / 2⌋) T ← join2(T)1, T2)
Tiempo de ejecución
Clasificación I{displaystyle Yo... no se considera en este análisis.
| # Niveles de recuperación | ▪ ▪ O()log k){displaystyle in O(log k)} |
| T(split) + T(join) | ▪ ▪ O()log SilencioTSilencio){displaystyle in O(log Silencio Silencioso)} |
| inserción por hilo | ▪ ▪ O()SilencioISilenciok){displaystyle in Oleft({frac ¿Qué? |
| T(insert) | ▪ ▪ O()log SilencioTSilencio){displaystyle in O(log Silencio Silencioso)} |
| T(bulkInsert) con k{displaystyle k} = Procesadores | ▪ ▪ O()log klog SilencioTSilencio+SilencioISilencioklog SilencioTSilencio){displaystyle in Oleft(log klog ¿Qué? |
Esto se puede mejorar utilizando algoritmos paralelos para dividir y unirse. En este caso el tiempo de ejecución es ▪ ▪ O()log SilencioTSilencio+SilencioISilencioklog SilencioTSilencio){displaystyle in Oleft(log Новывыхыхfrac ¿Qué?.
Trabajo
| #splits, #joins | ▪ ▪ O()k){displaystyle in O(k)} |
| W(split) + W(join) | ▪ ▪ O()log SilencioTSilencio){displaystyle in O(log Silencio Silencioso)} |
| #insertions | ▪ ▪ O()SilencioISilencio){displaystyle in O(vivienda)} |
| W(insert) | ▪ ▪ O()log SilencioTSilencio){displaystyle in O(log Silencio Silencioso)} |
| W(bulkInsert) | ▪ ▪ O()klog SilencioTSilencio+SilencioISilenciolog SilencioTSilencio){displaystyle in O(klog TENSI TENEDO ANTERIVISIÓNI soportalog NOVEDAD TENIDO |
Conducción
Otro método para paralelizar operaciones masivas es utilizar un enfoque de segmentación. Esto se puede hacer dividiendo la tarea de procesar una operación básica en una secuencia de subtareas. Para múltiples operaciones básicas, las subtareas se pueden procesar en paralelo asignando cada subtarea a un procesador separado.
- Primero el vracs I{displaystyle Yo... los elementos a insertar deben ser ordenados.
- Para cada elemento en I{displaystyle Yo... el algoritmo localiza la posición de inserción de acuerdo en T{displaystyle T}. Esto se puede hacer en paralelo para cada elemento ▪ ▪ I{displaystyle in I} desde entonces T{displaystyle T} no será mutado en este proceso. Ahora I{displaystyle Yo... debe dividirse en subsecuencias S{displaystyle S. según la posición de inserción de cada elemento. Por ejemplo sn,left{displaystyle s_{n,{mathit {left}} es la subsequencia de I{displaystyle Yo... que contiene los elementos cuya posición de inserción sería a la izquierda del nodo n{displaystyle n}.
- El elemento medio mn,dir{displaystyle m_{n,{mathit {dir}}} de cada subsequence sn,dir{displaystyle s_{n,{mathit {dir}}} se insertará en T{displaystyle T} como nuevo nodo n.{displaystyle n'}. Esto se puede hacer en paralelo para cada uno mn,dir{displaystyle m_{n,{mathit {dir}}} desde por definición la posición de inserción de cada mn,dir{displaystyle m_{n,{mathit {dir}}} es único. Si sn,dir{displaystyle s_{n,{mathit {dir}}} contiene elementos a la izquierda o a la derecha mn,dir{displaystyle m_{n,{mathit {dir}}}, que se incluirán en un nuevo conjunto de subsecuencias S{displaystyle S. como sn.,left{displaystyle s_{n',{Mathit {left}} o sn.,right{displaystyle s_{n',{mthit {right}}.
- Ahora T{displaystyle T} Posiblemente contiene hasta dos nodos rojos consecutivos al final de los caminos forman la raíz de las hojas, que necesita ser reparada. Tenga en cuenta que, mientras se repara, la posición de inserción de elementos ▪ ▪ S{displaystyle in S} debe ser actualizado, si los nodos correspondientes son afectados por rotaciones.
Si dos nodos tienen diferentes antepasados negros más cercanos, pueden ser reparados en paralelo. Como a la mayoría de los cuatro nodos puede tener el mismo antepasado negro más cercano, los nodos al nivel más bajo se pueden reparar en un número constante de pasos paralelos.
Este paso se aplicará sucesivamente a los niveles negros arriba hasta T{displaystyle T} está completamente reparado. - Los pasos 3 a 5 se repetirán en las nuevas subsecuencias hasta S{displaystyle S. está vacío. En este punto cada elemento ▪ ▪ I{displaystyle in I} ha sido insertado. Cada aplicación de estos pasos se llama a etapa. Desde la longitud de las subsecuencias en S{displaystyle S. es ▪ ▪ O()SilencioISilencio){displaystyle in O(vivienda)} y en cada etapa las subsecuencias están siendo cortadas en la mitad, el número de etapas es ▪ ▪ O()log SilencioISilencio){displaystyle in O(log SilencioI habit)}.
Dado que todas las etapas suben a los niveles negros del árbol, pueden ser paralelizadas en un oleoducto. Una vez que una etapa ha terminado de procesar un nivel negro, la siguiente etapa es capaz de subir y continuar a ese nivel.
Tiempo de ejecución
Clasificación I{displaystyle Yo... no se considera en este análisis. También, SilencioISilencio{displaystyle TENSIA se supone que es más pequeño que SilencioTSilencio{displaystyle Silencioso, de lo contrario sería más eficiente construir el árbol resultante desde cero.
| T(Posición de inserción final) | ▪ ▪ O()log SilencioTSilencio){displaystyle in O(log Silencio Silencioso)} |
| #Stages | ▪ ▪ O()log SilencioISilencio){displaystyle in O(log SilencioI habit)} |
| T(insert) + T(repair) | ▪ ▪ O()log SilencioTSilencio){displaystyle in O(log Silencio Silencioso)} |
| T(bulkInsert) con SilencioISilencio{displaystyle TENSIA ~ Procesadores | ▪ ▪ O()log SilencioISilencio+2⋅ ⋅ log SilencioTSilencio){displaystyle in O(log vulnerableI habit+2cdot log vulnerable)} =O()log SilencioTSilencio){displaystyle =O(log ANTERIOR ANTERIOR)} |
Trabajo
| W(Posiciones de inserción definidas) | ▪ ▪ O()SilencioISilenciolog SilencioTSilencio){displaystyle in O(PrincipalidadI sobreviviólog Неных)} |
| #insertions, #repairs | ▪ ▪ O()SilencioISilencio){displaystyle in O(vivienda)} |
| W(insert) + W(repair) | ▪ ▪ O()log SilencioTSilencio){displaystyle in O(log Silencio Silencioso)} |
| W(bulkInsert) | ▪ ▪ O()2⋅ ⋅ SilencioISilenciolog SilencioTSilencio){displaystyle in O(2cdot SilencioI sobrevivirlog Новованых)} =O()SilencioISilenciolog SilencioTSilencio){displaystyle =O(PrincipalidadI sobreviviólog Нованых)} |
Cultura popular
Se hizo referencia correctamente a un árbol rojo-negro en un episodio de Missing, como señaló Robert Sedgewick en una de sus conferencias:
- Jess:
Era la puerta roja otra vez.
Pollock:Pensé que la puerta roja era el contenedor de almacenamiento.
Jess:Pero ya no era rojo, era negro.
Antonio:¿Qué significa el giro rojo a negro?
Pollock:Déficit presupuestario, tinta roja, tinta negra.
Antonio:Podría ser de un árbol de búsqueda binario. El árbol rojo-negro rastrea cada camino sencillo de un nodo a una hoja descendente que tiene el mismo número de nodos negros.
Jess:¿Eso te ayuda con las damas?
Referencias y notas
- ^ a b c d James Paton. "Red-Black Trees".
- ^ a b rebalancing only (no lookup), see Tarjan and Mehlhorn.
- ^ a b Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "Red-Black Trees". Introducción a los algoritmos (segunda edición). MIT Press. pp. 273–301. ISBN 978-0-262-03293-3.
- ^ Morris, John (1998). "Red-Black Trees". Estructuras de datos y algoritmos.
- ^ Rudolf Bayer (1972). "Tareas binarias simétricas: estructura de datos y algoritmos de mantenimiento". Acta Informatica. 1 (4): 290-306. doi:10.1007/BF00289509. S2CID 28836825.
- ^ Drozdek, Adam (2001). Estructuras de datos y algoritmos en Java (2 ed.). Sams Publishing. p. 323. ISBN 978-0534376680.
- ^ a b Leonidas J. Guibas y Robert Sedgewick (1978). "Un Marco Dicromático para los Árboles Equilibrados". Proceedings of the 19th Annual Symposium on Foundations of Computer Science. pp. 8–21. doi:10.1109/SFCS.1978.3.
- ^ "Arboles Negros Rojos". eternamente confundido.com. Archivado desde el original el 2007-09-27. Retrieved 2015-09-02.
- ^ Robert Sedgewick (2012). Red-Black BSTs. Coursera.
Mucha gente pregunta por qué usamos el nombre rojo-negro. Bueno, inventamos esta estructura de datos, esta manera de ver árboles equilibrados, en Xerox PARC que era el hogar de la computadora personal y muchas otras innovaciones con las que vivimos hoy entrando interfaces gráficas de usuario, programas ethernet y orientados al objeto [sic] y muchas otras cosas. Pero una de las cosas que se inventó fue la impresión láser y estábamos muy emocionados de tener impresora láser de color cercano que podría imprimir las cosas en color y fuera de los colores que el rojo parecía lo mejor. Por eso elegimos el color rojo para distinguir los enlaces rojos, los tipos de enlaces, en tres nodos. Por lo tanto, esa es una respuesta a la pregunta para las personas que han estado haciendo.
- ^ "¿De dónde viene el término "Árbol Rojo/Blanco"?. programmers.stackexchange.com. Retrieved 2015-09-02.
- ^ Andersson, Arne (1993-08-11). "Los árboles de búsqueda se hicieron simples". En Dehne, Frank; Sack, Jörg-Rüdiger; Santoro, Nicola; Whitesides, Sue (eds.). Algoritmos y estructuras de datos (Proceedings). Notas de conferencia en Ciencias de la Computación. Vol. 709. Springer-Verlag Berlin Heidelberg. pp. 60–71. CiteSeerX10.1.1.118.6192. doi:10.1007/3-540-57155-8_236. ISBN 978-3-540-57155-1. Archivado desde el original en 2018-12-08. Alt URL
- ^ Okasaki, Chris (1999-01-01). "Arboles rojo-negro en un entorno funcional". Journal of Functional Programming. 9 (4): 471-477. doi:10.1017/S0956796899003494. ISSN 1469-7653. Archivado desde el original (PS) en 2007-09-26. Retrieved 2007-05-13.
- ^ Sedgewick, Robert (1983). Algoritmos (1a edición). Addison-Wesley. ISBN 978-0-201-06672-2.
- ^ Sedgewick, Robert; Wayne, Kevin. "RedBlackBST.java". algs4.cs.princeton.edu. Retrieved 7 de abril 2018.
- ^ Sedgewick, Robert (2008). "Left-leaning Red-Black Trees".
- ^ a b c Sedgewick, Robert; Wayne, Kevin (2011). Algoritmos (4a edición). Addison-Wesley Professional. ISBN 978-0-321-57351-3.
- ^ a b c d Mehlhorn, Kurt; Sanders, Peter (2008). "7. Secuencias clasificadas" (PDF). Algoritmos y estructuras de datos: La caja de herramientas básica. Berlín/Heidelberg: Springer. CiteSeerX10.1.1.148.2305. doi:10.1007/978-3-540-77978-0. ISBN 978-3-540-77977-3.
- ^ a b Cormen, Thomas; Leiserson, Charles; Rivest, Ronald; Stein, Clifford (2022). "13. Árboles rojos y negros". Introducción a los algoritmos (4a edición). MIT Press. pp. 331–332. ISBN 9780262046305.
- ^ Utilizando la definición de orden de Knuth: el número máximo de niños
- ^ Sedgewick, Robert (1998). Algoritmos en C++. Addison-Wesley Professional. pp. 565-575. ISBN 978-0-201-35088-3.
- ^ "La implementación de la epola (1)". Septiembre de 2014.
- ^ Pfaff 2004
- ^ a b "Robert Sedgewick" (PDF). Cs.princeton.edu. Retrieved 26 de marzo 2022.
- ^ "Arboles inclinados" (PDF). Cs.princeton.edu. Retrieved 26 de marzo 2022.
- ^ Demaine, E. D.; Harmon, D.; Iacono, J.; Pătraşcu, M. (2007). "Optimidad Dinámica—casi" (PDF). SIAM Journal on Computing. 37 (1): 240. doi:10.1137/S0097539705447347. S2CID 1480961.
- ^ "Cómo funciona un HashMap en JAVA". coding-geek.com.
- ^ Tarjan, Robert Endre (abril de 1985). "Complejidad Computacional Mortizada" (PDF). SIAM Journal on Algebraic and Discrete Methods. 6 (2): 306-318. doi:10.1137/0606031.
- ^ Lo importante de estas rotaciones de árboles es que preservan la secuencia ordenada de los nodos del árbol.
- ^ "Ben Pfaff (2007): Versión HTML en línea de una colección bien documentada de árboles de búsqueda binaria y rutinas equilibradas de biblioteca de árboles".
- ^ a b Las columnas izquierdas contienen mucho menos nodos que las derechas, especialmente para la eliminación. Esto indica que se puede obtener cierta eficiencia sacando la primera iteración de los lazos reequilibrantes de inserción y eliminación, porque muchos de los nodos nombrados son los nodos NIL en la primera iteración y definitivamente no NL posterior. (Ver también esta observación.)
- ^ Las rotaciones se han colocado antes de recolorar por razones de claridad. Pero los dos conmutadores, para que sea libre elección mover la rotación a la cola.
- ^ a b El mismo tabique se encuentra en Ben Pfaff.
- ^ Dinesh P. Mehta, Sartaj Sahni (Ed.) Manual de estructuras y aplicaciones de datos 10.4.2
- ^ Igualdad en el límite superior sostiene para los mínimos árboles RB2k de altura 2⋅ ⋅ k{displaystyle 2cdot k} con n=2⋅ ⋅ 2k− − 2{displaystyle n=2cdot 2}2} nodos y sólo para esos. Así que la desigualdad es marginalmente más precisa que la generalizada <math alttext="{displaystyle hh.2log2 ()n+1),{displaystyle h identificado2log _{2}(n+1),}<img alt="{displaystyle h por ejemplo, en Cormen p. 264.
Además, estos árboles son árboles binarios que admiten una y una única coloración conforme a los requisitos de RB 1 a 4. Pero hay más árboles tales, por ejemplo, pasar un nodo de niño a una hoja negra siempre lo obliga al rojo. (Un árbol RB mínimo de extraña altura permite cambiar el color de la raíz de rojo a negro.) - ^ a b Blelloch, Guy E.; Ferizovic, Daniel; Sun, Yihan (2016), "Sólo Únete a los conjuntos ordenados de paralelo" (PDF), Simposium on Parallel Algorithms and Architectures, Proc. of 28th ACM Symp. Algoritmos y arquitecturas paralelos (SPAA 2016), ACM, págs. 253 a 264, arXiv:1602.02120, doi:10.1145/2935764.2935768, ISBN 978-1-4503-4210-0, S2CID 2897793.
- ^ Park, Heejin; Park, Kunsoo (2001). " algoritmos paralelos para los árboles rojo-negro". Theoretical Computer Science. 262 (1–2): 415–435. doi:10.1016/S0304-3975(00)00287-5.
Nuestro algoritmo paralelo para construir un árbol rojo-negro de una lista ordenada n{displaystyle n} artículos corren O()1){displaystyle O(1)} tiempo con n{displaystyle n} procesadores en el CRCW PRAM y se ejecuta en O()log log n){displaystyle O(log log n)} tiempo con n/log log n{displaystyle n/log log n} procesadores en el EREW PRAM.
- ^ Sanders, Peter (2019). Mehlhorn, Kurt; Dietzfelbinger, Martin; Dementiev, Roman (eds.). Algoritmos y estructuras de datos secuenciales y paralelos: La caja de herramientas básica. Springer eBooks. Cham: Springer. pp. 252–253. doi:10.1007/978-3-030-25209-0. ISBN 9783030252090. S2CID 201692657.
- ^ Akhremtsev, Yaroslav; Sanders, Peter (2016). "Fast Parallel Operations on Search Trees". HiPC 2016, la 23a Conferencia Internacional de IEEE sobre Computación de Alto Rendimiento, Datos y Análisis, Hyderabad, India, diciembre, 19-22. IEEE, Piscataway (NJ): 291–300. arXiv:1510.05433. Bibcode:2015arXiv151005433A. ISBN 978-1-5090-5411-4.
- ^ Jájá, Joseph (1992). Una introducción a algoritmos paralelos. Reading, Mass. [u.a.]: Addison-Wesley. pp. 65–70. ISBN 0201548569.
- ^ Desaparecido (serie de televisión canadiense). A, W Network (Canadá); Lifetime (Estados Unidos).
- ^ Robert Sedgewick (2012). B-Trees. Coursera. 9:48 minutos.
Así que no sólo hay alguna emoción en ese diálogo, sino que también es técnicamente correcto que no se encuentra con las matemáticas en la cultura popular de la ciencia informática. Un árbol rojo-negro rastrea cada camino simple de un nodo a una hoja descendente con el mismo número de nodos negros que tienen derecho.
Contenido relacionado
Ciclo de vida de lanzamiento de software
Protocolo punto-a-punto
Formato de punto flotante de doble precisión