Árbol AVL

ImprimirCitar

Animación mostrando la inserción de varios elementos en un árbol AVL. Incluye rotaciones izquierda, derecha, izquierda e izquierda.

Fig. 1: Árbol AVL con factores de equilibrio (verde)

En la informática, una Árbol AVL (llamado después de inventores ADelson...VElsky y Landis) es un árbol de búsqueda binaria auto-Balancing. Fue la primera estructura de datos que se inventó. En un árbol AVL, las alturas de los dos subárboles infantiles de cualquier nodo difieren en la mayoría de uno; si en cualquier momento difieren por más de uno, se rebalancing se hace para restaurar esta propiedad. Lookup, insertion, and deletion all take $O(log) n)$ tiempo en el promedio y los peores casos, donde ${displaystyle n}$ es el número de nodos en el árbol antes de la operación. Las inserciones y eliminaciones pueden requerir que el árbol sea rebalanceado por una o más rotaciones de árboles.

El árbol AVL lleva el nombre de sus dos inventores soviéticos, Georgy Adelson-Velsky y Evgenii Landis, quienes lo publicaron en su artículo de 1962 "Un algoritmo para la organización de la información".

Los árboles AVL se comparan a menudo con los árboles rojo-negro porque ambos soportan el mismo conjunto de operaciones y toman ${displaystyle {text{O}}(log n)}$ tiempo para las operaciones básicas. Para aplicaciones de alta intensidad de búsqueda, los árboles AVL son más rápidos que los árboles negros rojos porque son más estrictamente equilibrados. Similar a los árboles rojo-negro, los árboles AVL son equilibrados de altura. Ambos son, en general, ni equilibrados de peso ni ${displaystyle mu }$ - balanceado para cualquier ${displaystyle mu leq {tfrac {1}{2}}}$ ; es decir, los nodos hermanos pueden tener un número enormemente diferente de descendientes.

Definición

Factor de equilibrio

En un árbol binario, el factor de equilibrio de un nodo X se define como la diferencia de altura

{displaystyle {text{BF}}(X):={text{Height} {text{RightSubtree}(X))-{text{Height}}} {text{LeftSubtree}}(X)}

de sus dos subárboles secundarios. Un árbol binario se define como un árbol AVL si el invariante

{displaystyle {text{BF}(X)in {{-1,0,1}}}

es válido para cada nodo X en el árbol.

Un nodo X con ${displaystyle {text{BF} {cH00FF} {fnMicrosoft Sans Serif}$ se llama "left-heavy", uno con ${displaystyle {text{BF}(X)}0}$ se llama "derecha-derecha", y uno con ${displaystyle {text{BF}(X)=0}$ es a veces simplemente llamado "balanceado".

Propiedades

Los factores de equilibrio se pueden mantener actualizados conociendo los factores de equilibrio anteriores y el cambio de altura; no es necesario conocer la altura absoluta. Para mantener la información del saldo de AVL, dos bits por nodo son suficientes.

La altura ${displaystyle h}$ (contada como el número máximo de niveles) de un árbol AVL con ${displaystyle n}$ nodos se encuentra en el intervalo:

{displaystyle log _{2}(n+1)leq h buscadolog _{varphi }(n+2)+b}

Donde ${displaystyle varphi:={tfrac {1+{sqrt {5} {2}approx 1.618}$ es la relación de oro y ${displaystyle b:={frac {log {2}{2}{2log _{2}varphi }-2approx ;-0.3277.}$ Esto es porque un árbol de altura AVL ${displaystyle h}$ contiene al menos ${displaystyle F_{h}-1}$ nodos donde ${displaystyle {fn} {fn} {N}$ es la secuencia de Fibonacci con los valores de semilla ${displaystyle F_{1}=F_{2}=1.$

Operaciones

Las operaciones de solo lectura de un árbol AVL implican realizar las mismas acciones que se llevarían a cabo en un árbol de búsqueda binaria desequilibrado, pero las modificaciones tienen que observar y restaurar el equilibrio de altura de los subárboles.

Buscando

La búsqueda de una clave específica en un árbol AVL se puede realizar de la misma manera que en cualquier árbol de búsqueda binario balanceado o no balanceado. Para que la búsqueda funcione de manera efectiva, debe emplear una función de comparación que establezca un pedido total (o al menos un pedido anticipado total) en el conjunto de claves. El número de comparaciones requeridas para una búsqueda exitosa está limitado por la altura $h$ y para una búsqueda fallida está muy cerca de $h$ , por lo que ambos están en $O(log n)$ .

Transversal

Como operación de solo lectura, el recorrido de un árbol AVL funciona de la misma manera que en cualquier otro árbol binario. Al explorar todos los $n$ nodos del árbol, se visita cada enlace exactamente dos veces: una visita hacia abajo para ingresar al subárbol en el que se basa ese nodo, otra visita hacia arriba para salir de ese nodo. subárbol del nodo después de haberlo explorado.

Una vez que se ha encontrado un nodo en un árbol AVL, se puede acceder al nodo siguiente o anterior en tiempo constante amortizado. Algunos ejemplos de exploración de estos "cercanos" los nodos requieren atravesar hasta enlaces $h \propto log(n)$ (particularmente cuando se navega desde la hoja más a la derecha de la raíz&# el subárbol izquierdo del 39 hasta la raíz o desde la raíz hasta la hoja más a la izquierda del subárbol derecho de la raíz; en el árbol AVL de la figura 1, al navegar desde el nodo P hasta el nodo próximo a la derecha, Q toma 3 pasos). Dado que hay enlaces $n -1$ en cualquier árbol, el costo amortizado es $2\times(n-1)/ n$ , o aproximadamente 2.

Insertar

Al insertar un nodo en un árbol AVL, inicialmente sigue el mismo proceso que al insertarlo en un árbol de búsqueda binaria. Si el árbol está vacío, el nodo se inserta como la raíz del árbol. Si el árbol no está vacío, bajamos por la raíz y recursivamente bajamos por el árbol buscando la ubicación para insertar el nuevo nodo. Este recorrido está guiado por la función de comparación. En este caso, el nodo siempre reemplaza una referencia NULL (izquierda o derecha) de un nodo externo en el árbol, es decir, el nodo se convierte en un hijo izquierdo o derecho del nodo externo.

Después de esta inserción, si un árbol se desequilibra, solo se desequilibran los ancestros del nodo recién insertado. Esto se debe a que solo esos nodos tienen alterados sus subárboles. Por lo tanto, es necesario verificar la consistencia de cada uno de los ancestros del nodo con las invariantes de los árboles AVL: esto se denomina "retracing". Esto se logra considerando el factor de equilibrio de cada nodo.

Dado que con una sola inserción la altura de un subárbol AVL no puede aumentar en más de uno, el factor de equilibrio temporal de un nodo después de una inserción estará en el rango [–2,+2 ]. Para cada nodo verificado, si el factor de equilibrio temporal permanece en el rango de -1 a +1, solo se necesita una actualización del factor de equilibrio y no se necesita rotación. Sin embargo, si el factor de equilibrio temporal es ±2, el subárbol enraizado en este nodo está AVL desequilibrado y se necesita una rotación. Con la inserción como muestra el código a continuación, la rotación adecuada inmediatamente reequilibra perfectamente el árbol.

En la figura 1, al insertar el nuevo nodo Z como hijo del nodo X, la altura de ese subárbol Z aumenta de 0 a 1.

Invariante del bucle de retracción para una inserción

La altura del subárbol enraizado por Z ha aumentado en 1. Ya está en forma AVL.

Código de ejemplo para una operación de inserción
para ()X = padre()Z); X ! nulo; X = padre()Z) {} // Loop (posiblemente hasta la raíz) // BF(X) tiene que ser actualizado: si ()Z == right_child()X) {} // El subárbol derecho aumenta si ()BF()X) ■ 0) {} // X es de buen corazón // == Confía en el BF(X) temporal == +2 // ===Se requiere rebalancing. G = padre()X); // Guardar padre de X alrededor de rotaciones si ()BF()Z) . 0) / Caso de izquierda derecha (ver figura 3) N = girar_RightLeft()X, Z); // Doble rotación: Derecha(Z) luego Izquierda(X) más Caso derecho (véase el gráfico 2) N = rotar_ Izquierda()X, Z); // Rotación individual izquierda(X) // Después de la rotación adapte el enlace padre } más {} si ()BF()X) . 0) {} BF()X) = 0; // El aumento de la altura de Z se absorbe en X. descanso; // Deja el bucle } BF()X) = +1; Z = X; // Altura(Z) aumenta en 1 continuar; } } más {} // Z == left_child(X): el subárbol izquierdo aumenta si ()BF()X) . 0) {} // X es zurdo // == Confía en el BF(X) temporal == -2 // ===Se requiere rebalancing. G = padre()X); // Guardar padre de X alrededor de rotaciones si ()BF()Z) ■ 0) // Caso derecho izquierdo N = rotar_ Izquierda()X, Z); // Doble rotación: Izquierda(Z) luego Derecha(X) más // Caso izquierdo izquierdo N = rotar_ Bien.()X, Z); // rotación simple derecha(X) // Después de la rotación adapte el enlace padre } más {} si ()BF()X) ■ 0) {} BF()X) = 0; // El aumento de la altura de Z se absorbe en X. descanso; // Deja el bucle } BF()X) = -1; Z = X; // Altura(Z) aumenta en 1 continuar; } } // Después de una rotación adapte el enlace padre: // N es la nueva raíz del subárbol rotado // Altura no cambia: Altura(N) == Altura vieja(X) padre()N) = G; si ()G ! nulo) {} si ()X == left_child()G) left_child()G) = N; más right_child()G) = N; } más árbol-root = N; // N es la nueva raíz del árbol total descanso; // No hay caída, sólo ruptura; o continuar;}// A menos que el bucle se quede por rotura, la altura del árbol total aumenta en 1.

Código de ejemplo para una operación de inserción

para ()X = padre()Z); X ! nulo; X = padre()Z) {} // Loop (posiblemente hasta la raíz) // BF(X) tiene que ser actualizado: si ()Z == right_child()X) {} // El subárbol derecho aumenta si ()BF()X) ■ 0) {} // X es de buen corazón // == Confía en el BF(X) temporal == +2 // ===Se requiere rebalancing. G = padre()X); // Guardar padre de X alrededor de rotaciones si ()BF()Z) . 0) / Caso de izquierda derecha (ver figura 3) N = girar_RightLeft()X, Z); // Doble rotación: Derecha(Z) luego Izquierda(X) más Caso derecho (véase el gráfico 2) N = rotar_ Izquierda()X, Z); // Rotación individual izquierda(X) // Después de la rotación adapte el enlace padre } más {} si ()BF()X) . 0) {} BF()X) = 0; // El aumento de la altura de Z se absorbe en X. descanso; // Deja el bucle } BF()X) = +1; Z = X; // Altura(Z) aumenta en 1 continuar; } } más {} // Z == left_child(X): el subárbol izquierdo aumenta si ()BF()X) . 0) {} // X es zurdo // == Confía en el BF(X) temporal == -2 // ===Se requiere rebalancing. G = padre()X); // Guardar padre de X alrededor de rotaciones si ()BF()Z) ■ 0) // Caso derecho izquierdo N = rotar_ Izquierda()X, Z); // Doble rotación: Izquierda(Z) luego Derecha(X) más // Caso izquierdo izquierdo N = rotar_ Bien.()X, Z); // rotación simple derecha(X) // Después de la rotación adapte el enlace padre } más {} si ()BF()X) ■ 0) {} BF()X) = 0; // El aumento de la altura de Z se absorbe en X. descanso; // Deja el bucle } BF()X) = -1; Z = X; // Altura(Z) aumenta en 1 continuar; } } // Después de una rotación adapte el enlace padre: // N es la nueva raíz del subárbol rotado // Altura no cambia: Altura(N) == Altura vieja(X) padre()N) = G; si ()G ! nulo) {} si ()X == left_child()G) left_child()G) = N; más right_child()G) = N; } más árbol-root = N; // N es la nueva raíz del árbol total descanso; // No hay caída, sólo ruptura; o continuar;}// A menos que el bucle se quede por rotura, la altura del árbol total aumenta en 1.

Para actualizar los factores de equilibrio de todos los nodos, primero observe que todos los nodos que requieren corrección se encuentran de hijo a padre a lo largo de la ruta de la hoja insertada. Si el procedimiento anterior se aplica a los nodos a lo largo de este camino, comenzando desde la hoja, entonces cada nodo en el árbol volverá a tener un factor de equilibrio de -1, 0 o 1.

El retroceso puede detenerse si el factor de equilibrio se convierte en 0, lo que implica que la altura de ese subárbol permanece sin cambios.

Si el factor de equilibrio se convierte en ±1, la altura del subárbol aumenta en uno y el retroceso debe continuar.

Si el factor de equilibrio se convierte temporalmente en ±2, esto debe repararse mediante una rotación adecuada, después de lo cual el subárbol tiene la misma altura que antes (y su raíz el factor de equilibrio 0).

El tiempo requerido es $O(log n)$ para la búsqueda, más un máximo de $O(log n$ ) niveles de retroceso ( $O(1)$ en promedio) en el camino de regreso a la raíz, por lo que la operación se puede completar en O(log n) tiempo.

Eliminar

Los pasos preliminares para eliminar un nodo se describen en la sección Árbol de búsqueda binario#Eliminación. Allí, la eliminación efectiva del nodo sujeto o el nodo de reemplazo disminuye la altura del árbol hijo correspondiente de 1 a 0 o de 2 a 1, si ese nodo tiene un hijo.

A partir de este subárbol, es necesario comprobar la coherencia de cada uno de los ancestros con las invariantes de los árboles AVL. Esto se llama "retroceder".

Dado que con una sola eliminación la altura de un subárbol AVL no puede disminuir en más de uno, el factor de equilibrio temporal de un nodo estará en el rango de −2 a +2. Si el factor de equilibrio permanece en el rango de −1 a +1, se puede ajustar de acuerdo con las reglas AVL. Si se convierte en ±2, entonces el subárbol está desequilibrado y debe rotarse. (A diferencia de la inserción donde una rotación siempre equilibra el árbol, después de la eliminación, puede haber BF(Z) ≠ 0 (véanse las figuras 2 y 3), de modo que después de la rotación simple o doble apropiada, la altura del subárbol reequilibrado disminuye en un significado que el árbol tiene que ser reequilibrado de nuevo en el siguiente nivel superior.) Los diversos casos de rotaciones se describen en la sección Reequilibrio.

Invariante del bucle de retracción para una eliminación

La altura del subárbol enraizado por N ha disminuido en 1. Ya está en forma AVL.

Código de ejemplo para una operación de eliminación
para ()X = padre()N); X ! nulo; X = G) {} // Loop (posiblemente hasta la raíz) G = padre()X); // Guardar padre de X alrededor de rotaciones // BF(X) no ha sido actualizado todavía! si ()N == left_child()X) {} // el subárbol izquierdo disminuye si ()BF()X) ■ 0) {} // X es de buen corazón // == Confía en el BF(X) temporal == +2 // ===Se requiere rebalancing. Z = right_child()X); // Hermano de N (más alto por 2) b = BF()Z); si ()b . 0) / Caso de izquierda derecha (ver figura 3) N = girar_RightLeft()X, Z); // Doble rotación: Derecha(Z) luego Izquierda(X) más Caso derecho (véase el gráfico 2) N = rotar_ Izquierda()X, Z); // Rotación individual izquierda(X) // Después de la rotación adapte el enlace padre } más {} si ()BF()X) == 0) {} BF()X) = +1; // La disminución de la altura de N se absorbe en X. descanso; // Deja el bucle } N = X; BF()N) = 0; // Altura(N) disminuye en 1 continuar; } } más {} // (N == right_child(X)): El subárbol derecho disminuye si ()BF()X) . 0) {} // X es zurdo // == Confía en el BF(X) temporal == -2 // ===Se requiere rebalancing. Z = left_child()X); // Hermano de N (más alto por 2) b = BF()Z); si ()b ■ 0) // Caso derecho izquierdo N = rotar_ Izquierda()X, Z); // Doble rotación: Izquierda(Z) luego Derecha(X) más // Caso izquierdo izquierdo N = rotar_ Bien.()X, Z); // rotación simple derecha(X) // Después de la rotación adapte el enlace padre } más {} si ()BF()X) == 0) {} BF()X) = -1; // La disminución de la altura de N se absorbe en X. descanso; // Deja el bucle } N = X; BF()N) = 0; // Altura(N) disminuye en 1 continuar; } } // Después de una rotación adapte el enlace padre: // N es la nueva raíz del subárbol rotado padre()N) = G; si ()G ! nulo) {} si ()X == left_child()G) left_child()G) = N; más right_child()G) = N; } más árbol-root = N; // N es la nueva raíz del árbol total si ()b == 0) descanso; // La altura no cambia: Deja el bucle // Altura(N) disminuye por 1 (== Altura vieja(X)-1)}// Si 0) la altura del árbol total disminuye en 1.

Código de ejemplo para una operación de eliminación

para ()X = padre()N); X ! nulo; X = G) {} // Loop (posiblemente hasta la raíz) G = padre()X); // Guardar padre de X alrededor de rotaciones // BF(X) no ha sido actualizado todavía! si ()N == left_child()X) {} // el subárbol izquierdo disminuye si ()BF()X) ■ 0) {} // X es de buen corazón // == Confía en el BF(X) temporal == +2 // ===Se requiere rebalancing. Z = right_child()X); // Hermano de N (más alto por 2) b = BF()Z); si ()b . 0) / Caso de izquierda derecha (ver figura 3) N = girar_RightLeft()X, Z); // Doble rotación: Derecha(Z) luego Izquierda(X) más Caso derecho (véase el gráfico 2) N = rotar_ Izquierda()X, Z); // Rotación individual izquierda(X) // Después de la rotación adapte el enlace padre } más {} si ()BF()X) == 0) {} BF()X) = +1; // La disminución de la altura de N se absorbe en X. descanso; // Deja el bucle } N = X; BF()N) = 0; // Altura(N) disminuye en 1 continuar; } } más {} // (N == right_child(X)): El subárbol derecho disminuye si ()BF()X) . 0) {} // X es zurdo // == Confía en el BF(X) temporal == -2 // ===Se requiere rebalancing. Z = left_child()X); // Hermano de N (más alto por 2) b = BF()Z); si ()b ■ 0) // Caso derecho izquierdo N = rotar_ Izquierda()X, Z); // Doble rotación: Izquierda(Z) luego Derecha(X) más // Caso izquierdo izquierdo N = rotar_ Bien.()X, Z); // rotación simple derecha(X) // Después de la rotación adapte el enlace padre } más {} si ()BF()X) == 0) {} BF()X) = -1; // La disminución de la altura de N se absorbe en X. descanso; // Deja el bucle } N = X; BF()N) = 0; // Altura(N) disminuye en 1 continuar; } } // Después de una rotación adapte el enlace padre: // N es la nueva raíz del subárbol rotado padre()N) = G; si ()G ! nulo) {} si ()X == left_child()G) left_child()G) = N; más right_child()G) = N; } más árbol-root = N; // N es la nueva raíz del árbol total  si ()b == 0) descanso; // La altura no cambia: Deja el bucle  // Altura(N) disminuye por 1 (== Altura vieja(X)-1)}// Si 0) la altura del árbol total disminuye en 1.

El retroceso puede detenerse si el factor de equilibrio se convierte en ±1 (debe haber sido 0), lo que significa que la altura de ese subárbol permanece sin cambios.

Si el factor de equilibrio se vuelve 0 (debe haber sido ±1), entonces la altura del subárbol disminuye en uno y el retroceso debe continuar.

Si el factor de equilibrio se convierte temporalmente en ±2, esto debe repararse mediante una rotación adecuada. Depende del factor de equilibrio del hermano Z (el árbol hijo más alto en la figura 2) si la altura del subárbol disminuye en uno –y el retroceso debe continuar– o no cambia (si Z tiene el factor de equilibrio 0) y todo el árbol tiene forma de AVL.

El tiempo requerido es $O(log n)$ para la búsqueda, más un máximo de $O(log n)$ niveles de retroceso ( $O(1)$ en promedio) en el camino de regreso a la raíz, por lo que la operación se puede completar en O(log n) tiempo.

Operaciones fijas y operaciones masivas

Además de las operaciones de inserción, eliminación y búsqueda de un solo elemento, se han definido varias operaciones de conjuntos en árboles AVL: unión, intersección y diferencia de conjuntos. Luego, se pueden implementar operaciones masivas rápidas sobre inserciones o eliminaciones basadas en estas funciones establecidas. Estas operaciones de configuración se basan en dos operaciones auxiliares, Dividir y Unir. Con las nuevas operaciones, la implementación de árboles AVL puede ser más eficiente y altamente paralelizable.

La función Unirse en dos árboles AVL $t 1$ y $t 2$ y una clave $k$ devolverá un árbol que contiene todos los elementos en $t 1$ , $t 2$ así como $k$ . Requiere que $k$ sea mayor que todas las claves en $t 1$ y menor que todas las claves en $t 2$ . Si los dos árboles difieren en altura como máximo uno, Únete simplemente crea un nuevo nodo con el subárbol izquierdo $t 1$ , raíz $k$ y subárbol derecho $t 2$ . De lo contrario, suponga que $t 1$ es mayor que $t 2$ para más de uno (el otro caso es simétrico). Unirse sigue la columna derecha de $t 1$ hasta un nodo $c$ que se equilibra con $t 2$ . En este punto, un nuevo nodo con el hijo izquierdo $c$ , root $k$ y el elemento secundario derecho $t 2$ se crea para reemplazar a c. El nuevo nodo satisface la invariante AVL y su altura es uno mayor que $c$ . El aumento de altura puede aumentar la altura de sus ancestros, posiblemente invalidando el invariante AVL de esos nodos. Esto se puede arreglar con una doble rotación si no es válido en el padre o una sola rotación a la izquierda si no es válido más arriba en el árbol, en ambos casos restaurando la altura para cualquier otro nodo antepasado. Unirse requerirá como máximo dos rotaciones. El costo de esta función es la diferencia de las alturas entre los dos árboles de entrada.

Aplicación de Pseudocode para el algoritmo Join
función JoinRightAVL(T)_L, k, T_R) (l,k',c) = exponer_L) si (Altura(c)_R)+1) T' = Node(c,k,T_R) si (Altura(T') retorno Node(l,k',T') más retorno girarLeft(Nodo(l,k',rotateRight(T'))) más T' = JoinRightAVL(c,k,T_R) T'' = Node(l,k',T') si (Altura(T) = Altura(l)+1) retorno T. más retorno rotateLeft(T') función JoinLeftAVL(T)_L, k, T_R) /* simétrico para JoinRightAVL / función* Join(T)_L, k, T_R) si (Altura(T)_L) Altura(T)_R)+1) retorno JoinRightAVL(T)_L, k, T_R) si (Altura(T)_R) Altura(T)_L)+1) retorno JoinLeftAVL(T)_L, k, T_R) retorno Nodo(T)_L,k,T_R) Aquí Altura(v) es la altura de un subárbol (nodo) $v$ . (l,k,r) = extractos expuestos(v) $v$ 's left child $l$ , la llave $k$ de $v$ 's root, and the right child $r$ . Node(l,k,r) significa crear un nodo de niño izquierdo $l$ , clave $k$ , y niño derecho $r$ .

Aplicación de Pseudocode para el algoritmo Join

función JoinRightAVL(T)_L, k, T_R)
(l,k',c) = exponer_L)
 si (Altura(c)_R)+1)
T' = Node(c,k,T_R)
si (Altura(T') retorno Node(l,k',T')
más retorno girarLeft(Nodo(l,k',rotateRight(T')))
 más T' = JoinRightAVL(c,k,T_R)
T'' = Node(l,k',T')
 si (Altura(T) = Altura(l)+1) retorno T.
 más retorno rotateLeft(T')

función JoinLeftAVL(T)_L, k, T_R)
/* simétrico para JoinRightAVL */

función Join(T)_L, k, T_R)
 si (Altura(T)_L) Altura(T)_R)+1) retorno JoinRightAVL(T)_L, k, T_R)
 si (Altura(T)_R) Altura(T)_L)+1) retorno JoinLeftAVL(T)_L, k, T_R)
 retorno Nodo(T)_L,k,T_R)

Aquí Altura(v) es la altura de un subárbol (nodo) $v$ . (l,k,r) = extractos expuestos(v) $v$ 's left child $l$ , la llave $k$ de $v$ 's root, and the right child $r$ . Node(l,k,r) significa crear un nodo de niño izquierdo $l$ , clave $k$ , y niño derecho $r$ .

Para dividir un árbol AVL en dos árboles más pequeños, los más pequeños que la clave $k$ y los más grandes que la clave $k$ , primero dibuje una ruta desde la raíz insertando $k$ en el AVL. Después de esta inserción, todos los valores menores que $k$ se encontrarán a la izquierda de la ruta, y todos los valores mayores que $k$ se encontrará a la derecha. Al aplicar Join, todos los subárboles del lado izquierdo se fusionan de abajo hacia arriba usando claves en la ruta como nodos intermedios de abajo hacia arriba para formar el árbol izquierdo, y la parte derecha es asimétrica. El costo de Split es $O(log n)$ , orden de la altura del árbol.

Implementación de Pseudocode para el algoritmo Split
función Split(T,k) si (T = nil) retorno (nil,false, nil) (L,m, R) = exponer(T) si (k = m) retorno (L,true, R) si (k madem) (L',b,R') = Split(L,k) retorno (L',b,Join(R',m,R)) si (k]m) (L',b,R') = Split(R,k) retorno (Join(L,m,L'),b,R'))

Implementación de Pseudocode para el algoritmo Split

función Split(T,k)
 si (T = nil) retorno (nil,false, nil)
(L,m, R) = exponer(T)
 si (k = m) retorno (L,true, R)
 si (k madem)
(L',b,R') = Split(L,k)
 retorno (L',b,Join(R',m,R))
 si (k]m)
(L',b,R') = Split(R,k)
 retorno (Join(L,m,L'),b,R'))

La unión de dos árboles AVL $t 1$ y $t 2$ que representan conjuntos $A$ y $B$ , es un AVL $t que representa A \cup B .$

Aplicación de Pseudocode para el algoritmo de la Unión
función Union(t)₁, t₂): si t₁ = nil: retorno t₂ si t₂ = nil: retorno t₁(T)_., b, t_■Dividido₂, t₁.root) retorno Join(Union(left(t)₁), t_.), t₁.root, Union(right(t₁), t_■) Aquí, Split se presume que devolver dos árboles: uno que sostiene las llaves menos su clave de entrada, uno que sostiene las llaves mayores. (El algoritmo no es destructivo, pero también existe una versión destructiva en el lugar).

Aplicación de Pseudocode para el algoritmo de la Unión

función Union(t)₁, t₂):
 si t₁ = nil:
 retorno t₂ si t₂ = nil:
 retorno t₁(T)_., b, t_■Dividido₂, t₁.root)
 retorno Join(Union(left(t)₁), t_.), t₁.root, Union(right(t₁), t_■)

Aquí, Split se presume que devolver dos árboles: uno que sostiene las llaves menos su clave de entrada, uno que sostiene las llaves mayores. (El algoritmo no es destructivo, pero también existe una versión destructiva en el lugar).

El algoritmo para intersección o diferencia es similar, pero requiere la rutina auxiliar Join2 que es igual a Join pero sin la tecla central. En función de las nuevas funciones de unión, intersección o diferencia, se puede insertar o eliminar una clave o varias claves del árbol AVL. Dado que Split llama a Join pero no se ocupa directamente de los criterios de equilibrio de los árboles AVL, dicha implementación suele denominarse "basada en unión" implementación.

La complejidad de cada unión, intersección y diferencia es ${displaystyle {text{O}left(mlog left({n over m}+1right)right)}$ para árboles AVL de tamaños ${displaystyle m}$ y ${displaystyle n;(geq m)}$ . Más importante aún, ya que las llamadas recursivas a la unión, intersección o diferencia son independientes entre sí, se pueden ejecutar en paralelo con una profundidad paralela ${displaystyle {text{O} {log mlog n)}$ . Cuando ${displaystyle m=1}$ , la implementación basada en la unión tiene el mismo DAG computacional que la inserción y eliminación de un solo elemento.

Reequilibrio

Si durante una operación de modificación la diferencia de altura entre dos subárboles secundarios cambia, esto puede, siempre que sea < 2, se reflejará mediante una adaptación de la información de saldo en la matriz. Durante las operaciones de inserción y eliminación, puede surgir una diferencia de altura (temporal) de 2, lo que significa que el subárbol principal debe ser "reequilibrado". Las herramientas de reparación dadas son las llamadas rotaciones de árbol, porque mueven las teclas solo "verticalmente", de modo que la secuencia en orden ("horizontal") de las teclas se conserva completamente (que es esencial para un árbol de búsqueda binaria).

Sea X el nodo que tiene un factor de equilibrio (temporal) de −2 o +2. Se modificó su subárbol izquierdo o derecho. Sea Z el hijo superior (ver figuras 2 y 3). Tenga en cuenta que ambos niños están en forma AVL por hipótesis de inducción.

En caso de inserción, esta inserción le ha ocurrido a uno de los hijos de Z de manera que la altura de Z ha aumentado. En caso de eliminación, esta eliminación le ha sucedido al hermano t₁ de Z de manera que la altura de t₁, que ya era más baja, ha disminuido. (Este es el único caso en el que el factor de equilibrio de Z también puede ser 0).

Hay cuatro variantes posibles de la infracción:

Derecho	⟹ Z es un derecho	hijo de su padre X y BF(Z) ≥ 0
Izquierda izquierda	⟹ Z es un izquierda	hijo de su padre X y BF(Z) ≤ 0
Izquierda derecha	⟹ Z es un derecho	hijo de su padre X y BF(Z)
Izquierda derecha	⟹ Z es un izquierda	hijo de su padre X y BF(Z) 0

Y el reequilibrio se realiza de forma diferente:

Derecho	⟹ X es reequilibrado con un	simple	rotación `rotate_Left`	(véase el gráfico 2)
Izquierda izquierda	⟹ X es reequilibrado con un	simple	rotación `rotate_Right`	(Imagen de la figura 2)
Izquierda derecha	⟹ X es reequilibrado con un	doble	rotación `rotate_RightLeft`	(véase el gráfico 3)
Izquierda derecha	⟹ X es reequilibrado con un	doble	rotación `rotate_LeftRight`	(Imagen de la figura 3)

Por lo tanto, las situaciones se denotan como C B, donde C (= dirección del niño) y B (= saldo) provienen del conjunto { Izquierda, Derecha } con Derecha:= −Izquierda. La violación del equilibrio del caso C == B se repara con una simple rotación rotate_(−C), mientras que el caso C != B se repara con una doble rotación rotate_ CB.

El costo de una rotación, ya sea simple o doble, es constante.

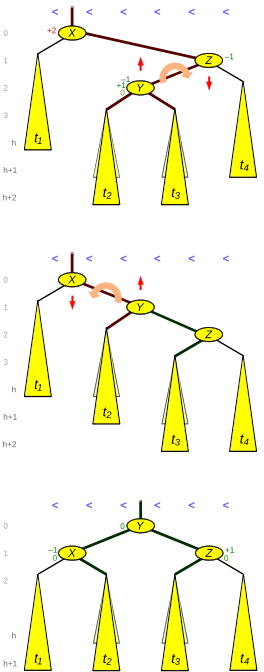
Rotación sencilla

La Figura 2 muestra una situación Derecha Derecha. En su mitad superior, el nodo X tiene dos árboles secundarios con un factor de equilibrio de +2. Además, el hijo interior t₂₃ de Z (es decir, hijo izquierdo cuando Z es hijo derecho o hijo derecho cuando Z es hijo izquierdo) no es mayor que su hermano t₄. Esto puede suceder por un aumento de la altura del subárbol t₄ o por una disminución de la altura del subárbol t₁. En el último caso, también puede ocurrir la situación pálida donde t₂₃ tiene la misma altura que t₄.

El resultado de la rotación a la izquierda se muestra en la mitad inferior de la figura. Se deben actualizar tres enlaces (bordes gruesos en la figura 2) y dos factores de equilibrio.

Como muestra la figura, antes de una inserción, la capa de hojas estaba en el nivel h+1, temporalmente en el nivel h+2 y después de la rotación nuevamente en el nivel h+1. En caso de deleción, la capa de hoja estaba en el nivel h+2, donde está nuevamente, cuando t₂₃ y t₄ tenían la misma altura. De lo contrario, la capa de hojas alcanza el nivel h+1, por lo que la altura del árbol girado disminuye.

Fig. 2: rotación simple
rotar_ Izquierda()X,Z)

Codigo snippet de una simple rotación izquierda

Entrada:	X = root of subtree to be rotated left
	Z = niño derecho de X, Z es sano
	con altura == $Altura(LeftSubtree($ X $)+2$
Resultado:	nueva raíz de subárbol rebalanceado

nodos *rotar_ Izquierda()nodos *X, nodos *Z) {} // Z es por 2 más alto que su hermano t23 = left_child()Z); // Niño interno de Z right_child()X) = t23; si ()t23 ! nulo) padre()t23) = X; left_child()Z) = X; padre()X) = Z; // 1er caso, BF(Z) == 0, // sólo ocurre con la eliminación, no la inserción: si ()BF()Z) == 0) {} // t23 ha sido de la misma altura que t4 BF()X) = +1; // t23 ahora más alto BF()Z) = –1; // t4 ahora inferior a X } más {} // 2o caso ocurre con la inserción o eliminación: BF()X) = 0; BF()Z) = 0; } retorno Z; // devolver nueva raíz del subárbol rotado}

Doble rotación

La Figura 3 muestra una situación de Derecha Izquierda. En su tercio superior, el nodo X tiene dos árboles secundarios con un factor de equilibrio de +2. Pero a diferencia de la figura 2, el niño interior Y de Z es más alto que su hermano t₄. Esto puede suceder por la inserción de la propia Y o por un aumento de altura de uno de sus subárboles t₂ o t₃ (con la consecuencia de que sean de diferente altura) o por una disminución de la altura del subárbol t₁. En este último caso, también puede ocurrir que t₂ y t₃ tengan la misma altura.

El resultado de la primera rotación, la derecha, se muestra en el tercio central de la figura. (Con respecto a los factores de equilibrio, esta rotación no es del mismo tipo que las otras rotaciones simples de AVL, porque la diferencia de altura entre Y y t₄ es solo 1). El resultado de la última izquierda la rotación se muestra en el tercio inferior de la figura. Se deben actualizar cinco enlaces (bordes gruesos en la figura 3) y tres factores de equilibrio.

Como muestra la figura, antes de una inserción, la capa de hojas estaba en el nivel h+1, temporalmente en el nivel h+2 y después de la doble rotación nuevamente en el nivel h+1. En caso de deleción, la capa de hojas estaba en el nivel h+2 y después de la doble rotación está en el nivel h+1, por lo que la altura del árbol rotado disminuye.

Fig. 3: Doble rotación girar_RightLeft()X,Z)
= rotar_ Bien. alrededor Z seguido
rotar_ Izquierda alrededor X

Codigo snippet de una rotación doble derecha-izquierda

Entrada:	X = root of subtree to be rotated
	Z = su hijo derecho, zurdo
	con altura == $Altura(LeftSubtree($ X $)+2$
Resultado:	nueva raíz de subárbol rebalanceado

nodos *girar_RightLeft()nodos *X, nodos *Z) {} // Z es por 2 más alto que su hermano Y = left_child()Z); // Niño interno de Z // Y es por 1 más alto que el hermano t3 = right_child()Y); left_child()Z) = t3; si ()t3 ! nulo) padre()t3) = Z; right_child()Y) = Z; padre()Z) = Y; t2 = left_child()Y); right_child()X) = t2; si ()t2 ! nulo) padre()t2) = X; left_child()Y) = X; padre()X) = Y; // 1er caso, BF(Y) == 0, // sólo ocurre con la eliminación, no la inserción: si ()BF()Y) == 0) {} BF()X) = 0; BF()Z) = 0; } más // otros casos ocurren con inserción o supresión: si ()BF()Y) ■ 0) {} // t3 era superior BF()X) = –1; // t1 ahora más alto BF()Z) = 0; } más {} // t2 era superior BF()X) = 0; BF()Z) = +1; // t4 ahora más alto } BF()Y) = 0; retorno Y; // devolver nueva raíz del subárbol rotado}

Comparación con otras estructuras

Tanto los árboles AVL como los árboles rojo-negro (RB) son árboles de búsqueda binaria autoequilibrados y están relacionados matemáticamente. De hecho, cada árbol AVL se puede colorear de rojo a negro, pero hay árboles RB que no están balanceados con AVL. Para mantener el AVL resp. Los invariantes del árbol RB, las rotaciones juegan un papel importante. En el peor de los casos, incluso sin rotaciones, las inserciones o eliminaciones de AVL o RB requieren $O(log n)$ inspecciones y/o actualizaciones de los factores de balance de AVL resp.. colores RB. Las inserciones y eliminaciones de RB y las inserciones de AVL requieren de cero a tres rotaciones recursivas de cola y se ejecutan en tiempo $O(1)$ amortizado, por lo tanto, igualmente constante en promedio. Las eliminaciones de AVL que requieren rotaciones $O(log n)$ en el peor de los casos también son $O(1)$ de media. Los árboles RB requieren almacenar un bit de información (el color) en cada nodo, mientras que los árboles AVL utilizan principalmente dos bits para el factor de equilibrio, aunque, cuando se almacenan en los hijos, es suficiente un bit con el significado «inferior al hermano». La mayor diferencia entre las dos estructuras de datos es su límite de altura.

Para un árbol de tamaño $n \geq 1$

la altura de un árbol AVL es en la mayoría
${displaystyle {begin{array}{ll}h sensibleleqqq;clog _{2}(n+d)+b\ccclog _{2}(n+2)+bend{array}}}}$

Donde

{displaystyle varphi:={tfrac {1+{sqrt {5} {2}approx 1.618}

la relación de oro,

{displaystyle c:={tfrac {1}{log Aprox 1.440,

{displaystyle b:={tfrac {c}{2}log _{2}5-2approx ;-0.328,}

{displaystyle *=1+{tfrac {1}{4}}approx 1.065}

la altura de un árbol RB es como máximo
${displaystyle {begin{array} {leqqq;2log _{2}(n+1)end{array}}}$ .

Los árboles AVL tienen un equilibrio más rígido que los árboles RB con una relación asintótica AVL/RB ≈0,720 de las alturas máximas. Para inserciones y deleciones, Ben Pfaff muestra en 79 medidas una relación AVL/RB entre 0,677 y 1,077 con mediana ≈0,947 y media geométrica ≈0,910.

Contenido relacionado

Más resultados...