Árbol autómata
Un autómata de árbol es un tipo de máquina de estado. Los autómatas de árbol se ocupan de las estructuras de árbol, en lugar de las cadenas de máquinas de estado más convencionales.
El siguiente artículo trata sobre los autómatas de árboles ramificados, que corresponden a los lenguajes regulares de los árboles.
Al igual que con los autómatas clásicos, los autómatas de árbol finito (FTA) pueden ser un autómata determinista o no. Según cómo el autómata procese el árbol de entrada, los autómatas de árbol finito pueden ser de dos tipos: (a) de abajo hacia arriba, (b) de arriba hacia abajo. Este es un tema importante, ya que aunque los autómatas de árbol no deterministas (ND) de arriba hacia abajo y ND de abajo hacia arriba son equivalentes en poder expresivo, los autómatas deterministas de arriba hacia abajo son estrictamente menos poderosos que sus contrapartes deterministas de abajo hacia arriba, porque las propiedades del árbol especificado por autómatas de árbol deterministas de arriba hacia abajo solo puede depender de las propiedades de la ruta. (Los autómatas de árbol ascendentes deterministas son tan poderosos como los autómatas de árbol ND).
Definiciones
Un autómata de árbol finito de abajo hacia arriba sobre F se define como una tupla (Q, F, Qf, Δ), donde Q es un conjunto de estados, F es un alfabeto clasificado (es decir, un alfabeto cuyos símbolos tienen una aridad asociada), Qf ⊆ Q es un conjunto de estados finales, y Δ es un conjunto de reglas de transición de la forma f(q1(x1),...,qn(xn)) → q( f(x1,...,xn)), para un n-ario f ∈ F, q, q Variables i ∈ Q y xi subárboles que denotan. Es decir, los miembros de Δ son reglas de reescritura de nodos cuyos elementos secundarios ' las raíces son estados, a los nodos cuyas raíces son estados. Así, el estado de un nodo se deduce de los estados de sus hijos.
Para n=0, es decir, para un símbolo constante f, la definición de la regla de transición anterior dice f() → q(f()); a menudo, los paréntesis vacíos se omiten por conveniencia: f → q(f). Dado que estas reglas de transición para símbolos constantes (hojas) no requieren un estado, no se necesitan estados iniciales definidos explícitamente. Un autómata de árbol de abajo hacia arriba se ejecuta en un término base sobre F, comenzando en todas sus hojas simultáneamente y moviéndose hacia arriba, asociando un estado de ejecución de Q con cada subtérmino. El término se acepta si su raíz está asociada a un estado de aceptación de Qf.
Un autómata de árbol finito de arriba hacia abajo sobre F se define como una tupla (Q, F, Qi, Δ), con dos diferencias con los autómatas de árbol de abajo hacia arriba. Primero, Qi ⊆ Q, el conjunto de sus estados iniciales, reemplaza a Qf; segundo, sus reglas de transición están orientadas a la inversa: q(f(x1,...,x n)) → f(q1(x1),...,qn(xn)), para una n-aria f ∈ F, q, qi ∈ Q y x i variables que denotan subárboles. Es decir, los miembros de Δ aquí reescriben las reglas desde los nodos cuyas raíces son estados a los nodos cuyas raíces secundarias son estados. Un autómata de arriba hacia abajo comienza en algunos de sus estados iniciales en la raíz y se mueve hacia abajo a lo largo de las ramas del árbol, asociando inductivamente a lo largo de una carrera un estado con cada subtérmino. Un árbol es aceptado si todas las ramas pueden pasar por este camino.
Un árbol autómata se llama determinista (abreviado DFTA) si no hay dos reglas de Δ que tengan el mismo lado izquierdo; de lo contrario, se denomina no determinista (NFTA). Los autómatas de árbol no deterministas de arriba hacia abajo tienen el mismo poder expresivo que los no deterministas de abajo hacia arriba; las reglas de transición simplemente se invierten y los estados finales se convierten en los estados iniciales.
Por el contrario, los autómatas de árbol deterministas de arriba hacia abajo son menos poderosos que sus contrapartes de abajo hacia arriba, porque en un autómata de árbol determinista no hay dos reglas de transición que tengan el mismo lado izquierdo. Para los autómatas de árbol, las reglas de transición son reglas de reescritura; y para los de arriba hacia abajo, el lado izquierdo serán los nodos principales. En consecuencia, un árbol autómata determinista de arriba hacia abajo solo podrá probar las propiedades del árbol que son verdaderas en todas las ramas, porque la elección del estado para escribir en cada rama secundaria se determina en el nodo principal, sin conocer el contenido de las ramas secundarias..
Los autómatas de árbol infinito extienden los autómatas de arriba hacia abajo a árboles infinitos y se pueden usar para probar la decidibilidad de S2S, la teoría monádica de segundo orden con dos sucesores. Los autómatas de árbol finitos (no deterministas si son de arriba hacia abajo) son suficientes para WS2S.
Ejemplos
Autómata ascendente que acepta listas booleanas
Emplear colores para distinguir los miembros de F y Q, y usar el alfabeto clasificado F={ falso,verdadero,<span style="color:#800000" ninguno, contras(.,.) }, con contras con aridad 2 y todos los demás símbolos con aridad 0, un autómata de árbol de abajo hacia arriba que acepta el conjunto de todas las listas finitas de valores booleanos se puede definir como (Q, F, Qf, Δ) con Q={ Bool,BLista }, Qf={ BList }, y Δ que consta de las reglas
| falso | → | Bool()falso) | 1) |
| verdadero | → | Bool()verdadero) | 2), |
| Nil | → | BList()Nil) | 3), y |
| cons()Bool(x1),BList(x2) | → | BList()cons(x1,x2) | (4). |
En este ejemplo, las reglas pueden entenderse intuitivamente como asignando a cada término su tipo de forma ascendente; p.ej. la regla (4) se puede leer como "Un término contras(x1 ,x2) tiene el tipo BList, siempre que x1 y x2 tiene tipo Bool y BList, respectivamente". Una ejecución de ejemplo de aceptación es
| cons() | falso, | cons() | verdadero, | Nil | ) | ||
| ⇒ | cons() | falso, | cons() | verdadero, | BList()Nil) | ) | 3) |
| ⇒ | cons() | falso, | cons() | Bool()verdadero), | BList()Nil) | ) | 2) |
| ⇒ | cons() | falso, | BList()cons() | verdadero, | Nil | )) | 4) |
| ⇒ | cons() | Bool()falso), | BList()cons() | verdadero, | Nil | )) | por (1) |
| ⇒ | BList()cons() | falso, | cons() | verdadero, | Nil | )) | por (4), aceptado. |
Cf. la derivación del mismo término de una gramática de árbol regular correspondiente al autómata, que se muestra en Gramática de árbol regular#Ejemplos.
Una ejecución de ejemplo de rechazo es
| cons() | falso, | verdadero | ) | ||
| ⇒ | cons() | falso, | Bool()verdadero) | ) | por (1) |
| ⇒ | cons() | Bool()falso), | Bool()verdadero) | ) | por 2), no se aplica otra norma. |
Intuitivamente, esto corresponde al término contras(falso,true) no está bien escrito.
Autómata de arriba hacia abajo que acepta múltiplos de 3 en notación binaria
| (A) | (B) | (C) | (D) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Stringgrammar reglas | Stringautomaton transiciones | Árbol autómata transiciones | Treegrammar reglas | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
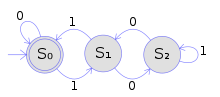
Usando la misma coloración que la anterior, este ejemplo muestra cómo los autómatas de árbol generalizan los autómatas de cadena ordinarios. El autómata de cadena determinista finito que se muestra en la imagen acepta todas las cadenas de dígitos binarios que denotan un múltiplo de 3. Usando las nociones de Autómata finito determinista # Definición formal, se define por:
- el conjunto Q de estados { S0, S1, S2 }
- el alfabeto de entrada { 0, 1 }
- el estado inicial S0,
- el conjunto de estados finales siendo { S0 }, y
- las transiciones que se muestran en la columna (B) del cuadro.
En la configuración del árbol autómata, el alfabeto de entrada se cambia de modo que los símbolos 0 y 1 son unarios y un símbolo nulo, digamos que nil se usa para las hojas de los árboles. Por ejemplo, la cadena binaria "110" en la configuración del autómata de cadenas corresponde al término "1(1(0(cero)))" en la configuración del árbol autómata; de esta manera, las cadenas se pueden generalizar a árboles o términos. El autómata de árbol finito de arriba hacia abajo que acepta el conjunto de todos los términos correspondientes a múltiplos de 3 en notación de cadena binaria se define entonces por:
- el conjunto Q de estados siendo todavía { S0, S1, S2 }
- el alfabeto de entrada clasificada { 0, 1, Nil Con Arity()0)=Arity()1)=1 y Arity()Nil)=0, como se explica,
- el conjunto de estados iniciales siendo { S0 }, y
- las transiciones que se muestran en la columna (C) del cuadro.
Por ejemplo, el árbol "1(1(0(cero)))" es aceptado por la siguiente ejecución del autómata de árbol:
| S0() | 1() | 1() | 0() | Nil | ))) | |||||
| ⇒ | 1() | S1() | 1() | 0() | Nil | ))) | por 2 | |||
| ⇒ | 1() | 1() | S0() | 0() | Nil | ))) | por 4 | |||
| ⇒ | 1() | 1() | 0() | S0() | Nil | ))) | por 1 | |||
| ⇒ | 1() | 1() | 0() | Nil | )) | por 0 |
Por el contrario, el término "1(0(ninguno))" conduce a la siguiente ejecución del autómata que no acepta:
| ⇒ S0() | 1() | 0() | Nil | )) | |||
| ⇒ | 1() | S1() | 0() | Nil | ))) | por 2 | |
| ⇒ | 1() | 0() | S2() | Nil | ))) | por 3, ninguna norma aplicable |
Dado que no hay otros estados iniciales que S0 para iniciar la ejecución de un autómata, el término "1(0( ninguno))" no es aceptado por el árbol autómata.
Para propósitos de comparación, la tabla da en la columna (A) y (D) una gramática regular (cadena) (derecha) y una gramática de árbol regular, respectivamente, cada una aceptando el mismo lenguaje que su contraparte autómata.
Propiedades
Reconocibilidad
Para un autómata ascendente, se acepta un término fundamental t (es decir, un árbol) si existe una reducción que comienza en t y termina en q(t), donde q es un estado final. Para un autómata de arriba hacia abajo, se acepta un término fundamental t si existe una reducción que comienza en q(t) y termina en t, donde q es un estado inicial.
El lenguaje del árbol L(A) aceptado, o reconocido, por un árbol autómata A es el conjunto de todos los términos básicos aceptados por A. Un conjunto de términos básicos es reconocible si existe un árbol autómata que lo acepte.
Un homomorfismo de árbol lineal (es decir, que preserva la aridad) preserva la reconocibilidad.
Integridad y reducción
Un autómata de árbol finito no determinista es completo si hay al menos una regla de transición disponible para cada combinación posible de símbolo y estado. Un estado q es accesible si existe un término fundamental t tal que existe una reducción de t a q(t). Un NFTA es reducido si todos sus estados son accesibles.
Lema de bombeo
Cada término fundamental suficientemente grande t en un lenguaje de árbol reconocible L se puede tripartitar verticalmente de tal manera que la repetición arbitraria ("bombeo") del término medio parte mantiene el término resultante en L.
Para el lenguaje de todas las listas finitas de valores booleanos del ejemplo anterior, todos los términos más allá del límite de altura k=2 pueden bombearse, ya que deben contener una ocurrencia de contras. Por ejemplo,
| cons()falso, | cons()verdadero,Nil) | ) | , |
| cons()falso,cons()falso, | cons()verdadero,Nil) | ) | , |
| cons()falso,cons()falso,cons()falso, | cons()verdadero,Nil) | )) | ,... |
todos pertenecen a ese idioma.
Cierre
La clase de lenguajes arbóreos reconocibles se cierra bajo unión, complementación e intersección.
Teorema de Myhill-Nerode
Una congruencia en el conjunto de todos los árboles sobre un alfabeto clasificado F es una relación de equivalencia tal que u1 ≡ v 1 y... y un ≡ vn implica f(u1,...,un) ≡ f(v1,..., vn), para cada f ∈ F. Es de índice finito si su número de clases de equivalencia es finito.
Para un árbol-lenguaje dado L, una congruencia puede ser definida por u ≡L v si C[u] ∈ L ⇔ C[v] ∈ L para cada contexto C.
El teorema de Myhill-Nerode para árboles autómatas establece que las siguientes tres afirmaciones son equivalentes:
- L es un árbol reconocible lenguaje
- L es la unión de algunas clases de equivalencia de una congruencia del índice finito
- la relaciónL es una congruencia del índice finito
Contenido relacionado
Multiplan
ZX80
Teorema de representación de Riesz