Arbelos

En geometría, un arbelos es una región plana delimitada por tres semicírculos con tres vértices de manera que cada esquina de cada semicírculo es compartida con una de las otras (conectadas), todas en el mismo lado de una línea recta (la línea base) que contiene sus diámetros.

La primera referencia conocida a esta figura se encuentra en el Libro de Lemas de Arquímedes, donde algunas de sus propiedades matemáticas se establecen como Proposiciones 4 a 8. La palabra arbelos en griego significa "cuchillo de zapatero". La figura está estrechamente relacionada con la cadena Pappus.

Propiedades

Dos de los semicírculos son necesariamente cóncavos, con diámetros arbitrarios a y b; el tercer semicírculo es convexo, con diámetro a+b.

Área

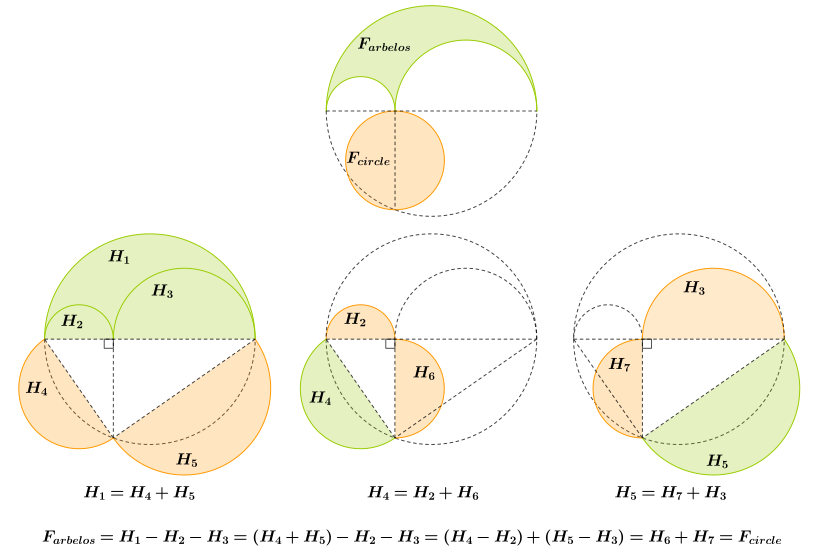
El área de los arbelos es igual al área de un círculo con diámetro JA.

Prueba: Para la prueba, refleje los arbelos sobre la línea a través de los puntos B y C, y observar que el doble del área de los arbelos es lo que queda cuando las áreas de los dos círculos más pequeños (con diámetros BA, AC) se restan de la zona del círculo grande (con diámetro BC). Puesto que el área de un círculo es proporcional a la plaza del diámetro (Euclid's Elements, Libro XII, Proposición 2; no necesitamos saber que la constante de proporcionalidad es π/4), el problema se reduce a mostrar que ${displaystyle 2 turbaya sobre la muerte.$. La longitud SilencioBCSilencio iguala la suma de las longitudes SilencioBASilencio y SilencioACSilencio, por lo que esta ecuación simplifica algebraicamente a la afirmación de que ${displaystyle Silencio.$. Así pues, la reclamación es que la duración del segmento AH es la media geométrica de las longitudes de los segmentos BA y AC. Ahora (ver Figura) el triángulo BHC, siendo inscrito en el semicírculo, tiene un ángulo recto en el punto H (Euclid, Book III, Proposition 31), y consecuentemente SilencioHASilencio es de hecho un "mean proporcional" entre SilencioBASilencio y SilencioACSilencio (Euclid, Libro VI, Proposición 8, Porismo). Esta prueba aproxima el argumento griego antiguo; Harold P. Boas cita un papel de Roger B. Nelsen que implementó la idea como la siguiente prueba sin palabras.

Rectángulo

Sean D y E< /span> sean los puntos donde se encuentran los segmentos BH y CH intersectan los semicírculos AB y AC, respectivamente. El cuadrilátero ADHE es en realidad un rectángulo.

Prueba: ∠BDA, ∠BHC, y ∠AEC son ángulos rectos porque están inscritos en semicírculos (por el teorema de Thales). El cuadrilátero ADHE por lo tanto tiene tres ángulos rectos, por lo que es un rectángulo. Q.E.D.

Tangentes

La línea DE es tangente al semicírculo BA en D y semicírculo AC en E.

Prueba: Desde ∠BDA es un ángulo recto, ∠DBA iguales π/2 menos ∠DAB. Sin embargo, ∠DAH también iguales π/2 menos ∠DAB (since ∠HAB es un ángulo recto). Por lo tanto triángulos DBA y DAH son similares. Por lo tanto ∠DIA iguales ∠DOH, donde I es el punto medio de BA y O es el punto medio de AH. Pero... ∠AOH es una línea recta, así que ∠DOH y ∠DOA son ángulos complementarios. Por lo tanto la suma de ∠DIA y ∠DOA es π. ∠IAO es un ángulo recto. La suma de los ángulos en cualquier cuadrilátero es 2π, así que en cuadrilátero IDOA, ∠IDO Debe ser un ángulo recto. Pero... ADHE es un rectángulo, así que el punto medio O de AH (la diagonal del rectángulo) es también el punto medio de DE (el rectángulo es otro diagonal). As I (definido como punto medio de BA) es el centro de semicírculo BA, y ángulo IDEIDE es un ángulo recto, entonces DE es tangente a semicircle BA a D. Por razonamiento análogo DE es tangente a semicircle AC a E. Q.E.D.

Arquímedes N#39; círculos

La altitud AH divide los arbelos en dos regiones, cada una delimitada por un semicírculo, un segmento de línea recta y un arco. del semicírculo exterior. Los círculos inscritos en cada una de estas regiones, conocidos como círculos de Arquímedes. Los círculos de los arbelos, tienen el mismo tamaño.

Variaciones y generalizaciones

El parbelos es una figura similar al arbelos, que utiliza segmentos de parábola en lugar de semicírculos. Una generalización que comprende tanto arbelos como parbelos es la f-belos, que utiliza un cierto tipo de funciones diferenciables similares.

En el modelo de semiplano de Poincaré del plano hiperbólico, un arbelos modela un triángulo ideal.

Etimología

El nombre arbelos proviene del griego ἡ ἄρβηλος he árbēlos o ἄρβυλος árbylos, que significa "cuchillo de zapatero'. 34;, un cuchillo utilizado por los zapateros desde la antigüedad hasta nuestros días, cuya hoja se dice que se asemeja a la figura geométrica.