Antepasado común más bajo

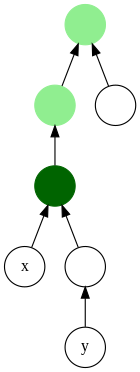
En teoría de grafos y ciencias de la computación, el ancestro común más bajo (LCA) (también llamado ancestro común mínimo) de dos nodos v y w en un árbol o grafo acíclico dirigido (DAG) T es el nodo más bajo (es decir, el más profundo) que tiene tanto v como w como descendientes, donde definimos cada nodo como un descendiente de sí mismo (por lo que si v tiene una conexión directa con w, w es el ancestro común más bajo).

El LCA de v y w en T es el ancestro compartido de v y w que se encuentra más alejado de la raíz. El cálculo de los ancestros comunes más bajos puede ser útil, por ejemplo, como parte de un procedimiento para determinar la distancia entre pares de nodos en un árbol: la distancia de v a w se puede calcular como la distancia desde la raíz a v, más la distancia desde la raíz a w, menos el doble de la distancia desde la raíz a su ancestro común más bajo (Djidjev, Pantziou y Zaroliagis 1991).

En una estructura de datos de árbol donde cada nodo apunta a su padre, el ancestro común más bajo se puede determinar fácilmente al encontrar la primera intersección de las rutas desde v y w hasta la raíz. En general, el tiempo computacional requerido para este algoritmo es O(h) donde h es la altura del árbol (longitud de la ruta más larga desde una hoja hasta la raíz). Sin embargo, existen varios algoritmos para procesar árboles de modo que los ancestros comunes más bajos se puedan encontrar más rápidamente. El algoritmo de ancestros comunes más bajos fuera de línea de Tarjan, por ejemplo, preprocesa un árbol en tiempo lineal para proporcionar consultas LCA de tiempo constante. En general, existen algoritmos similares en los DAG, pero con una complejidad superlineal.

El problema del ancestro común más bajo fue definido por Alfred Aho, John Hopcroft y Jeffrey Ullman (1973), pero Dov Harel y Robert Tarjan (1984) fueron los primeros en desarrollar una estructura de datos de ancestro común más bajo óptimamente eficiente. Su algoritmo procesa cualquier árbol en tiempo lineal, utilizando una descomposición de ruta pesada, de modo que las consultas subsiguientes sobre el ancestro común más bajo puedan ser respondidas en tiempo constante por consulta. Sin embargo, su estructura de datos es compleja y difícil de implementar. Tarjan también encontró un algoritmo más simple pero menos eficiente, basado en la estructura de datos de unión-búsqueda, para calcular los ancestros comunes más bajos de un lote fuera de línea de pares de nodos.

Baruch Schieber y Uzi Vishkin (1988) simplificaron la estructura de datos de Harel y Tarjan, lo que dio lugar a una estructura implementable con los mismos límites de tiempo de consulta y preprocesamiento asintótico. Su simplificación se basa en el principio de que, en dos tipos especiales de árboles, los ancestros comunes más bajos son fáciles de determinar: si el árbol es un camino, entonces el ancestro común más bajo se puede calcular simplemente a partir del mínimo de los niveles de los dos nodos consultados, mientras que si el árbol es un árbol binario completo, los nodos se pueden indexar de tal manera que los ancestros comunes más bajos se reduzcan a operaciones binarias simples sobre los índices. La estructura de Schieber y Vishkin descompone cualquier árbol en una colección de caminos, de modo que las conexiones entre los caminos tienen la estructura de un árbol binario, y combina estas dos técnicas de indexación más simples.

Omer Berkman y Uzi Vishkin (1993) descubrieron una forma completamente nueva de responder a las consultas de mínimo común ancestro, logrando nuevamente un tiempo de preprocesamiento lineal con un tiempo de consulta constante. Su método implica formar un recorrido de Euler de un grafo formado a partir del árbol de entrada duplicando cada arista y usar este recorrido para escribir una secuencia de números de nivel de los nodos en el orden en que el recorrido los visita; una consulta de mínimo común ancestro puede luego transformarse en una consulta que busca el valor mínimo que ocurre dentro de algún subintervalo de esta secuencia de números. Luego manejan este problema de consulta de rango mínimo (RMQ) combinando dos técnicas, una técnica basada en precalcular las respuestas a intervalos grandes que tienen tamaños que son potencias de dos, y la otra basada en la búsqueda en tablas para consultas de intervalo pequeño. Este método fue presentado más tarde en una forma simplificada por Michael Bender y Martin Farach-Colton (2000). Como habían observado previamente Gabow, Bentley & Tarjan (1984), el problema del rango mínimo puede a su vez transformarse nuevamente en un problema de ancestro común más bajo utilizando la técnica de árboles cartesianos.

Alstrup et al. (2004) y Fischer & Heun (2006) realizaron simplificaciones adicionales.

Sleator y Tarjan (1983) propusieron la variante dinámica de LCA del problema en el que la estructura de datos debe estar preparada para manejar las consultas LCA intermixed con operaciones que cambian el árbol (es decir, reorganizar el árbol añadiendo y eliminando los bordes). Esta variante se puede resolver en ${\displaystyle O(\log N)}$ tiempo en el tamaño total del árbol para todas las modificaciones y consultas. Esto se hace manteniendo el bosque utilizando la estructura de datos de árboles dinámicos con partición por tamaño; esto mantiene una descomposición de luz pesada de cada árbol, y permite que las consultas LCA se realicen en tiempo logarítmico en el tamaño del árbol.

Como se mencionó anteriormente, el ACV se puede reducir a RMQ. Una solución eficiente para el problema de RMQ resultante comienza por dividir la secuencia numérica en bloques. Se utilizan dos técnicas diferentes para las consultas entre bloques y dentro de los bloques.

La reducción del ACV a RMQ comienza recorriendo el árbol. Para cada nodo visitado, registre en secuencia su etiqueta y profundidad. Supongamos que los nodos x e y se encuentran en las posiciones i y j en esta secuencia, respectivamente. Entonces, el ACV de x e y se encontrará en la posición RMQ(i, j), donde el RMQ se toma sobre los valores de profundidad.

A pesar de que existe una solución en tiempo constante y en espacio lineal para RMQ general, se puede aplicar una solución simplificada que haga uso de las propiedades del ACV. Esta solución simplificada solo se puede utilizar para RMQ reducido a partir del ACV.

Similar a la solución mencionada anteriormente, dividimos la secuencia en cada bloque ${\displaystyle B_{i}$, donde cada bloque ${\displaystyle B_{i}$ tiene tamaño ${\displaystyle b={1\over 2}\log n}$.

Al dividir la secuencia en bloques, la ${\displaystyle RMQ(i,j)}$ query puede resolverse resolviendo dos casos diferentes:

Para responder ${\displaystyle RMQ(i,j)}$ consulta en caso uno, hay 3 grupos de variables precomputadas para ayudar a reducir el tiempo de consulta.

Primero, el elemento mínimo con el índice más pequeño en cada bloque ${\displaystyle B_{i}$ es precomputado y denotado como ${\displaystyle Y...$. Un conjunto de ${\displaystyle Y...$ tomas ${\displaystyle O(n/b)}$ espacio.

Segundo, dado el conjunto de ${\displaystyle Y...$, la consulta RMQ para este conjunto es precomputada utilizando la solución con tiempo constante y espacio linearitmico. Hay ${\displaystyle n/b}$ bloques, así que la mesa de búsqueda en esa solución toma ${\displaystyle O({n \over b}\log {n \over b})}$ espacio. Porque... ${\displaystyle b={1\over 2}\log n}$, ${\displaystyle O({n \over b}\log {n \over b})}$ = ${\displaystyle O(n)}$ espacio. Por lo tanto, la consulta RMQ precomputada utilizando la solución con tiempo constante y espacio linearitmico en estos bloques sólo toma ${\displaystyle O(n)}$ espacio.

Tercero, en cada bloque ${\displaystyle B_{i}$, vamos ${\displaystyle K_{i}$ ser un índice en ${\displaystyle B_{i}$ tales que ${\displaystyle 0\leq kiectob}$. Para todos ${\displaystyle K_{i}$ desde ${\displaystyle 0}$ hasta ${\displaystyle b}$, bloque ${\displaystyle B_{i}$ se divide en dos intervalos ${\displaystyle [0,k_{i}}$ y ${\displaystyle [k_{i},b}$. Luego el elemento mínimo con el índice más pequeño para intervalos en ${\displaystyle [0,k_{i}}$ y ${\displaystyle [k_{i},b}$ en cada bloque ${\displaystyle B_{i}$ es precomputado. Tales elementos mínimos se llaman prefijo min para el intervalo en ${\displaystyle [0,k_{i}}$ y sufijo min para el intervalo en ${\displaystyle [k_{i},b}$. Cada iteración de ${\displaystyle K_{i}$ calcula un par de prefijo min y sufijo min. Por lo tanto, el número total de prefijos min y sufijo mins en un bloque ${\displaystyle B_{i}$ es ${\displaystyle 2b}$. Ya que hay ${\displaystyle n/b}$ bloques, en total, todos los prefijo min y sufijo min arrays tomar ${\displaystyle O(2b\cdot {n\over b}}$ que es ${\displaystyle O(n)}$ espacios.

En total, se necesita ${\displaystyle O(n)}$ espacio para almacenar los 3 grupos de variables precomputadas mencionadas anteriormente.

Por lo tanto, respondiendo al ${\displaystyle RMQ(i,j)}$ query in case 1 is simply tasking the minimum of the following three questions:

Vamos. ${\displaystyle B_{i}$ ser el bloque que contiene el elemento en el índice ${\displaystyle i}$, y ${\displaystyle B_{j}$ para índice ${\displaystyle j}$.

1. El sufijo min en ${\displaystyle [i\mod b,b]$ en el bloque${\displaystyle B_{i}$
2. Respuesta a la consulta RMQ en un subconjunto de ${\displaystyle y}$s de bloques ${\displaystyle #$utilizando la solución con tiempo constante y espacio linearitmico
3. El prefijo min en ${\displaystyle [0,j\mod b)}$ en el bloque ${\displaystyle B_{j}$

Las tres preguntas pueden responderse en tiempo constante. Por lo tanto, el caso 1 puede responderse en espacio lineal y tiempo constante.

La secuencia de RMQ que se redujo a partir de LCA tiene una propiedad que un RMQ normal no tiene. El siguiente elemento siempre es +1 o -1 desde el elemento actual. Por ejemplo:

Por lo tanto, cada bloque ${\displaystyle B_{i}$ se puede codificar como un bitstring con 0 representa la profundidad actual -1, y 1 representa la profundidad actual +1. Esta transformación convierte un bloque ${\displaystyle B_{i}$en un pedacito de tamaño ${\displaystyle b-1}$. Un pedacito de tamaño ${\displaystyle b-1}$ tiene ${\displaystyle 2^{b-1}$ posibles mordeduras. Desde ${\displaystyle b={1\over 2}\log n}$, entonces ${\displaystyle 2^{b-1}\leq 2^{b}=2^{1\over 2}\log n}=n^{1\over 2}={\sqrt {n}}$.

Por lo tanto, ${\displaystyle B_{i}$ es siempre uno de los ${\displaystyle {\sqrt {n}}$ posible mordedura con tamaño de ${\displaystyle b-1}$.

Luego, para cada posible bitstrings, aplicamos la ingenua solución de tiempo constante espacio cuadrático. Esto va a tomar ${\displaystyle {\sqrt {n}\cdot b^{2}$ espacios, que es ${\displaystyle O({\sqrt {n}\cdot (\log n)^{2})\leq O({\sqrt {n}\cdot {\sqrt {n})=O(n)}$.

Por lo tanto, respondiendo al ${\displaystyle RMQ(i,j)}$ la consulta en el caso 2 es simplemente encontrar el bloque correspondiente (en el que es un bitstring) y realizar una búsqueda de tabla para ese bitstring. Por lo tanto, el caso 2 se puede resolver utilizando espacio lineal con tiempo de búsqueda constante.

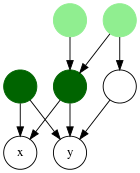
Si bien el concepto de ancestro común más bajo se estudió originalmente en el contexto de los árboles, se puede definir para los grafos acíclicos dirigidos (DAG), utilizando cualquiera de dos definiciones posibles. En ambas, se supone que los bordes del DAG apuntan de los padres a los hijos.

• Dado G =V, E), Aït-Kaci et al. (1989) define a poset ()V, ≤ tales que x ≤ Sí. Sip x es accesible desde Sí.. Los antepasados más bajos comunes de x y Sí. son entonces los elementos mínimos bajo ≤ del conjunto de ancestro común {}z ▪ V Silencio x ≤ z y Sí. ≤ z}.
• Bender et al. (2005) dieron una definición equivalente, donde los antepasados comunes más bajos de x y Sí. son los nodos de cero en el subgrafo del G inducido por el conjunto de antepasados comunes x y Sí..

En un árbol, el ancestro común más bajo es único; en un DAG de n nodos, cada par de nodos puede tener hasta n-2 ACV (Bender et al. 2005), mientras que la existencia de un ACV para un par de nodos ni siquiera está garantizada en DAG conectados arbitrariamente.

Aït-Kaci et al. (1989) ofrecen un algoritmo de fuerza bruta para encontrar el ancestro común más bajo: se encuentran todos los ancestros de x e y y, a continuación, se devuelve el elemento máximo de la intersección de los dos conjuntos. Existen mejores algoritmos que, de forma análoga a los algoritmos LCA en árboles, preprocesan un gráfico para permitir consultas LCA de tiempo constante. El problema de la existencia de LCA se puede resolver de forma óptima para DAG dispersos mediante un algoritmo O(|V||E|) creado por Kowaluk y Lingas (2005).

Dash et al. (2013) presentan un marco unificado para el preprocesamiento de grafos acíclicos dirigidos con el fin de calcular un ancestro común más bajo representativo en un DAG con raíz en tiempo constante. Su marco puede lograr tiempos de preprocesamiento casi lineales para grafos dispersos y está disponible para uso público.

El problema de calcular los ancestros comunes más bajos de las clases en una jerarquía de herencia surge en la implementación de sistemas de programación orientada a objetos (Aït-Kaci et al. 1989). El problema del ACV también encuentra aplicaciones en modelos de sistemas complejos que se encuentran en la computación distribuida (Bender et al. 2005).

• Problema del antepastor de nivel
• Semilattice

• Aho, Alfred; Hopcroft, John; Ullman, Jeffrey (1973), "Al encontrar ancestros comunes más bajos en los árboles", Proc. 5th ACM Symp. Theory of Computing (STOC), pp. 253–265, doi:10.1145/800125.804056S2CID 17705738.
• Aït-Kaci, H.; Boyer, R.; Lincoln, P.; Nasr, R. (1989), "Efficient implementation of lattice operations" (PDF), Transacciones ACM en la programación de idiomas y sistemas, 11 (1): 115–146, CiteSeerX 10.1.1.106.4911, doi:10.1145/59287.59293, S2CID 2931984.
• Alstrup, Stephen; Gavoille, Cyril; Kaplan, Haim; Rauhe, Theis (2004), "Nearest Common Ancestors: A Survey and a New Algorithm for a Distributed Environment", Theory of Computing Systems, 37 (3): 441–456, CiteSeerX 10.1.1.76.5973, doi:10.1007/s00224-004-1155-5, S2CID 9447127. Una versión preliminar apareció en SPAA 2002.
• Bender, Michael A.; Farach-Colton, Martin (2000), "The LCA problem revisited", Proceedings of the 4th Latin American Symposium on Theoretical Informatics, Notas de conferencias en ciencias de la informática, vol. 1776, Springer-Verlag, págs. 88 a 94, doi:10.1007/10719839_9, ISBN 978-3-540-67306-4.
• Bender, Michael A.; Farach-Colton, Martín; Pemmasani, Giridhar; Skiena, Steven; Sumazin, Pavel (2005), "Ancestros comunes más bajos en árboles y gráficos acíclicos dirigidos" (PDF), Journal of Algorithms, 57 (2): 75–94, doi:10.1016/j.jalgor.2005.08.001.
• Berkman, Omer; Vishkin, Uzi (1993), "Recursive Star-Tree Parallel Data Structure", SIAM Journal on Computing, 22 (2): 221–242, doi:10.1137/0222017, archivado desde el original el 23 de septiembre de 2017.
• Dash, Santanu Kumar; Scholz, Sven-Bodo; Herhut, Stephan; Christianson, Bruce (2013), "Un enfoque escalable para calcular el ancestro común más representativo en gráficos acíclicos dirigidos" (PDF), Theoretical Computer Science, 513: 25–37, doi:10.1016/j.tcs.2013.09.030, hdl:2299/12152
• Djidjev, Hristo N.; Pantziou, Grammati E.; Zaroliagis, Christos D. (1991), "Computing shortest paths and distances in planar graphs", Automata, Idiomas y Programación: 18o Coloquio Internacional, Madrid, España, 8 al 12 de julio de 1991, Notas de Conferencias en Ciencias de la Computación, vol. 510, Springer, págs. 327 a 338, doi:10.1007/3-540-54233-7_145, ISBN 978-3-540-54233-9.
• Fischer, Johannes; Heun, Volker (2006), "Mejores teóricos y prácticos en el proyecto RMQ, con aplicaciones a LCA y LCE", Proceedings of the 17th Annual Symposium on Combinatorial Pattern Matching, Notas de Conferencias en Ciencias de la Computación, vol. 4009, Springer-Verlag, págs. 36 a 48, CiteSeerX 10.1.1.64.5439, doi:10.1007/11780441_5, ISBN 978-3-540-35455-0.
• Gabow, Harold N.; Bentley, Jon Louis; Tarjan, Robert E. (1984), "Scaling and related techniques for geometry problems", STOC '84: Proc. 16th ACM Symposium on Theory of Computing, New York, NY, USA: ACM, pp. 135–143, doi:10.1145/800057.808675, ISBN 978-08291CID.
• Harel, Dov; Tarjan, Robert E. (1984), " algoritmos rápidos para encontrar ancestros comunes más cercanos", SIAM Journal on Computing, 13 (2): 338–355, doi:10.1137/0213024.
• Kowaluk, Miroslaw; Lingas, Andrzej (2005), "LCA queries in directed acyclic graphs", en Caires, Luís; Italiano, Giuseppe F.; Monteiro, Luís; Palamidessi, Catuscia; Yung, Moti (eds.), Automata, Idiomas y Programación, 32o Coloquio Internacional, ICALP 2005, Lisboa, Portugal, 11-15 de julio 10.1.1.460.6923, doi:10.1007/11523468_20, ISBN 978-3-540-27580-0
• Schieber, Baruch; Vishkin, Uzi (1988), "Al encontrar ancestros comunes más bajos: simplificación y paralización", SIAM Journal on Computing, 17 (6): 1253–1262, doi:10.1137/0217079.
• Sleator, D. D.; Tarjan, R. E. (1983), "A Data Structure for Dynamic Trees" (PDF), Proceedings of the thirtyth annual ACM symposium on Theory of computing - STOC '81, págs. 114 a 122, doi:10.1145/800076.802464, S2CID 15402750

• Ancestro común más bajo de un árbol de búsqueda binaria, por Kamal Rawat
• Python implementación del algoritmo de Bender y Farach-Colton para árboles, por David Eppstein
• Aplicación de pitón para gráficos acíclicos arbitrarios dirigidos
• Notas de conferencias sobre los LCA de un MIT 2003 Curso Estructuras de datos. Curso de Erik Demaine, notas escritas por Loizos Miguel y Christos Kapoutsis. Notas de 2007 ofreciendo el mismo curso, escrito por Alison Cichowlas.
• Más bajo Ancestro Común en Árboles binarios en C. Una versión simplificada de la técnica Schieber-Vishkin que funciona sólo para árboles binarios equilibrados.
• Vídeo de Donald Knuth explicando la técnica Schieber-Vishkin
• Gama de Consultas Mínimas y Más bajo artículo de Ancestro Común en Topcoder
• Documentación para el paquete lca para Haskell por Edward Kmett, que incluye el algoritmo de la lista de acceso aleatorio skew-binary. Estructuras de datos puramente funcionales para diapositivas LCA en línea para el mismo paquete.