Ángulo inscrito

En geometría, un ángulo inscrito es el ángulo que se forma en el interior de un círculo cuando dos cuerdas se cruzan en el círculo. También se puede definir como el ángulo subtendido en un punto del círculo por dos puntos dados del círculo.

De manera equivalente, un ángulo inscrito se define por dos cuerdas del círculo que comparten un punto final.

El teorema del ángulo inscrito relaciona la medida de un ángulo inscrito con la del ángulo central que subtiende el mismo arco.

Showing translation for

The inscribed angle theorem appears as Proposition 20 on Book 3 of Euclid 's Elements.

Teorema

Declaración

El teorema del ángulo inscrito establece que un ángulo θ inscrito en un círculo es la mitad del ángulo central 2θ que subtiende el mismo arco en el círculo. Por lo tanto, el ángulo no cambia cuando su vértice se mueve a diferentes posiciones en el círculo.

Prueba

Ángulos inscritos donde una cuerda es un diámetro

Sea O el centro de un círculo, como en el diagrama de la derecha. Elige dos puntos del círculo y llámalos V y A. Dibuje la línea VO y extiéndala más allá de O para que cruce el círculo en el punto B que es diametralmente opuesto al punto V. Dibuja un ángulo cuyo vértice sea el punto V y cuyos lados pasen por los puntos A y B.

Dibuje la línea OA. El ángulo BOA es un ángulo central; llámalo θ. Las líneas OV y OA son radios del círculo, por lo que tienen longitudes iguales. Por lo tanto, el triángulo VOA es isósceles, por lo que el ángulo BVA (el ángulo inscrito) y el ángulo VAO son iguales; denotemos cada uno de ellos como ψ.

Los ángulos BOA y AOV suman 180°, ya que la línea VB que pasa por O es una recta. línea. Por lo tanto, el ángulo AOV mide 180° − θ.

Did you mean:

It is known that the three angles of a triangle add up to 180°, and the three angles of triangle VIA are:

180° - Silencio

↑

↑.

Por lo tanto,

2↑ ↑ +180∘ ∘ − − Silencio Silencio =180∘ ∘ .{displaystyle 2psi +180^{circ }-theta =180^{circ }

Restar

()180∘ ∘ − − Silencio Silencio ){displaystyle (180^{circ }-theta)}

de ambos lados,

2↑ ↑ =Silencio Silencio ,{displaystyle 2psi =theta}

donde θ es el ángulo central que subtiende el arco AB y ψ es el ángulo inscrito que subtiende el arco AB.

Ángulos inscritos con el centro del círculo en su interior

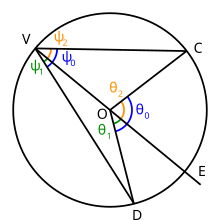
Dado un círculo cuyo centro es el punto O, elija tres puntos V, C y D en el círculo. Dibuja las líneas VC y VD: el ángulo DVC es un ángulo inscrito. Ahora dibuja la línea VO y extiéndela más allá del punto O para que cruce el círculo en el punto E. El ángulo DVC subtiende el arco DC en el círculo.

Supongamos que este arco incluye el punto E dentro de él. El punto E es diametralmente opuesto al punto V. Los ángulos DVE y EVC también son ángulos inscritos, pero ambos ángulos tienen un lado que pasa por el centro del círculo, por lo tanto, el teorema de la Parte 1 anterior puede ser aplicado a ellos.

Por lo tanto,

∠ ∠ DVC=∠ ∠ DVE+∠ ∠ EVC.{displaystyle angle DVC=angle DVE+angle EVC.}

entonces deja

↑ ↑ 0=∠ ∠ DVC,{displaystyle psi _{0}=angle DVC,}

↑ ↑ 1=∠ ∠ DVE,{displaystyle psi _{1}=angle DVE,}

↑ ↑ 2=∠ ∠ EVC,{displaystyle psi _{2}=angle EVC,}

para que

↑ ↑ 0=↑ ↑ 1+↑ ↑ 2.()1){displaystyle psi ¿Qué? _{1}+psi _{2}.qquad qquad (1)}

Did you mean:

Draw lines OC and OD. Angel DOC is a central angle, but so are angles DOE and EOC, and

∠ ∠ DOC=∠ ∠ DOE+∠ ∠ EOC.{displaystyle angle DOC=angle DOE+angle EOC.}

Dejar

Silencio Silencio 0=∠ ∠ DOC,{displaystyle theta ¿Qué?

Silencio Silencio 1=∠ ∠ DOE,{displaystyle theta ¿Qué?

Silencio Silencio 2=∠ ∠ EOC,{displaystyle theta ¿Qué?

para que

Silencio Silencio 0=Silencio Silencio 1+Silencio Silencio 2.()2){displaystyle theta ♪♪♪ _{1}+theta _{2}.qquad qquad (2)}

De la parte Uno que sabemos que Silencio Silencio 1=2↑ ↑ 1{displaystyle theta ¿Qué? ¿Qué? y eso Silencio Silencio 2=2↑ ↑ 2{displaystyle theta ¿Qué? ¿Qué?. Combinar estos resultados con rendimientos de ecuación (2)

Silencio Silencio 0=2↑ ↑ 1+2↑ ↑ 2=2()↑ ↑ 1+↑ ↑ 2){displaystyle theta ¿Qué? _{1}+2psi _{2}=2(psi _{1}+psi _{2}

por lo tanto, mediante la ecuación (1),

Silencio Silencio 0=2↑ ↑ 0.{displaystyle theta ¿Qué? _{0}

Ángulos inscritos con el centro del círculo en su exterior

Did you mean:

The previous case can be extended to cover the case where the measure of the inscribed angle is the difference between two inscribed angles as discussed in the first part of this proof.

Dado un círculo cuyo centro es el punto O, elija tres puntos V, C y D en el círculo. Dibuja las líneas VC y VD: el ángulo DVC es un ángulo inscrito. Ahora dibuja la línea VO y extiéndela más allá del punto O para que cruce el círculo en el punto E. El ángulo DVC subtiende el arco DC en el círculo.

Supongamos que este arco no incluye el punto E dentro de él. El punto E es diametralmente opuesto al punto V. Los ángulos EVD y EVC también son ángulos inscritos, pero ambos ángulos tienen un lado que pasa por el centro del círculo, por lo tanto, el teorema de la Parte 1 anterior puede ser aplicado a ellos.

Por lo tanto,

∠ ∠ DVC=∠ ∠ EVC− − ∠ ∠ EVD{displaystyle angle DVC=angle EVC-angle EVD}.

entonces deja

↑ ↑ 0=∠ ∠ DVC,{displaystyle psi _{0}=angle DVC,}

↑ ↑ 1=∠ ∠ EVD,{displaystyle psi _{1}=angle EVD,}

↑ ↑ 2=∠ ∠ EVC,{displaystyle psi _{2}=angle EVC,}

para que

↑ ↑ 0=↑ ↑ 2− − ↑ ↑ 1.()3){displaystyle psi ¿Qué? _{2}-psi ¿Qué?

Did you mean:

Draw lines OC and OD. Angle DOC is a central angle, but so are angles WORD and EOC, and

∠ ∠ DOC=∠ ∠ EOC− − ∠ ∠ EOD.{displaystyle angle DOC=angle EOC-angle EOD.}

Dejar

Silencio Silencio 0=∠ ∠ DOC,{displaystyle theta ¿Qué?

Silencio Silencio 1=∠ ∠ EOD,{displaystyle theta ¿Qué?

Silencio Silencio 2=∠ ∠ EOC,{displaystyle theta ¿Qué?

para que

Silencio Silencio 0=Silencio Silencio 2− − Silencio Silencio 1.()4){displaystyle theta ¿Qué? _{1}.qquad qquad (4)}

De la parte Uno que sabemos que Silencio Silencio 1=2↑ ↑ 1{displaystyle theta ¿Qué? ¿Qué? y eso Silencio Silencio 2=2↑ ↑ 2{displaystyle theta ¿Qué? ¿Qué?. Combinar estos resultados con rendimientos de ecuación (4)

Silencio Silencio 0=2↑ ↑ 2− − 2↑ ↑ 1{displaystyle theta - ¿Qué? ¿Qué?

por lo tanto, mediante la ecuación (3),

Silencio Silencio 0=2↑ ↑ 0.{displaystyle theta ¿Qué? _{0}

Corolario

Por un argumento similar, el ángulo entre una cuerda y la recta tangente en uno de sus puntos de intersección es igual a la mitad del ángulo central subtendido por la cuerda. Véase también Rectas tangentes a circunferencias.

Aplicaciones

El teorema del ángulo inscrito se utiliza en muchas demostraciones de la geometría euclidiana elemental del plano. Un caso especial del teorema es el de Tales. teorema, que establece que el ángulo subtendido por un diámetro es siempre de 90°, es decir, un ángulo recto. Como consecuencia del teorema, los ángulos opuestos de los cuadriláteros cíclicos suman 180°; por el contrario, cualquier cuadrilátero en el que esto sea cierto puede inscribirse en un círculo. Como otro ejemplo, el teorema del ángulo inscrito es la base de varios teoremas relacionados con la potencia de un punto con respecto a un círculo. Además, permite demostrar que cuando dos cuerdas se cruzan en un círculo, los productos de las longitudes de sus piezas son iguales.

Teoremas de ángulos inscritos para elipses, hipérbolas y parábolas

Did you mean:

Inscribed angle theorems exist for ellipses, hyperbolas and parabolas, to. The essential differences are the measurements of an angle. (An angle is considered a pair of intersecting lines.)

• Ellipse
• Hyperbola
• Parabola