Análisis tiempo-frecuencia

En el procesamiento de señales, el análisis tiempo-frecuencia comprende aquellas técnicas que estudian una señal tanto en el dominio del tiempo como en el de la frecuencia simultáneamente utilizando varias representaciones de tiempo-frecuencia. En lugar de ver una señal unidimensional (una función, real o de valor complejo, cuyo dominio es la línea real) y alguna transformada (otra función cuyo dominio es la línea real, obtenida del original mediante alguna transformada), tiempo-frecuencia El análisis estudia una señal bidimensional, una función cuyo dominio es el plano real bidimensional, obtenido de la señal mediante una transformada tiempo-frecuencia.

La motivación matemática para este estudio es que las funciones y su representación transformada están estrechamente relacionadas y pueden entenderse mejor estudiándolas conjuntamente, como un objeto bidimensional, en lugar de por separado. Un ejemplo sencillo es que la periodicidad cuádruple de la transformada de Fourier (y el hecho de que la transformada doble de Fourier invierte la dirección) puede interpretarse considerando la transformada de Fourier como una rotación de 90° en el plano tiempo-frecuencia asociado: 4 tales las rotaciones producen la identidad, y 2 de esas rotaciones simplemente invierten la dirección (reflexión a través del origen).

La motivación práctica para el análisis tiempo-frecuencia es que el análisis clásico de Fourier supone que las señales son infinitas en el tiempo o periódicas, mientras que muchas señales en la práctica son de corta duración y cambian sustancialmente a lo largo de su duración. Por ejemplo, los instrumentos musicales tradicionales no producen sinusoides de duración infinita, sino que comienzan con un ataque y luego decaen gradualmente. Esto está mal representado por los métodos tradicionales, lo que motiva el análisis tiempo-frecuencia.

Una de las formas más básicas de análisis tiempo-frecuencia es la transformada de Fourier de corto tiempo (STFT), pero se han desarrollado técnicas más sofisticadas, en particular wavelets y métodos de análisis espectral de mínimos cuadrados para datos espaciados de manera desigual.

Motivación

En el procesamiento de señales, el análisis tiempo-frecuencia es un conjunto de técnicas y métodos utilizados para caracterizar y manipular señales cuyas estadísticas varían en el tiempo, como las señales transitorias.

Es una generalización y refinamiento del análisis de Fourier, para el caso en que las características de frecuencia de la señal varían con el tiempo. Dado que muchas señales de interés (como el habla, la música, las imágenes y las señales médicas) tienen características de frecuencia cambiantes, el análisis tiempo-frecuencia tiene un amplio alcance de aplicaciones.

Mientras que la técnica de la transformada de Fourier se puede ampliar para obtener el espectro de frecuencia de cualquier señal localmente integrable de crecimiento lento, este enfoque requiere una descripción completa del comportamiento de la señal en todo el tiempo. De hecho, se puede pensar que los puntos en el dominio de la frecuencia (espectral) agrupan información de todo el dominio del tiempo. Si bien matemáticamente elegante, esta técnica no es apropiada para analizar una señal con un comportamiento futuro indeterminado. Por ejemplo, uno debe presuponer algún grado de comportamiento futuro indeterminado en cualquier sistema de telecomunicaciones para lograr una entropía distinta de cero (si uno ya sabe lo que dirá la otra persona, no puede aprender nada).

Para aprovechar el poder de una representación de frecuencia sin la necesidad de una caracterización completa en el dominio del tiempo, primero se obtiene una distribución tiempo-frecuencia de la señal, que representa la señal en los dominios de tiempo y frecuencia simultáneamente. En tal representación, el dominio de la frecuencia solo reflejará el comportamiento de una versión temporalmente localizada de la señal. Esto permite hablar con sensatez de señales cuyas frecuencias componentes varían en el tiempo.

Por ejemplo, en lugar de utilizar distribuciones templadas para transformar globalmente la siguiente función en el dominio de la frecuencia, se podrían utilizar estos métodos para describirla como una señal con una frecuencia que varía en el tiempo.

${\displaystyle x(t)={\begin{cases}\cos(\pi t); correspondió10\\cos(3\pi t); tercero10\leq t won20\\\cos(2\pi t); contigua 20\end{cases}}$

Una vez que dicha representación ha sido generada otras técnicas en el análisis de frecuencia-tiempo puede ser aplicada a la señal para extraer información de la señal, para separar la señal de ruido o interferir señales, etc.

Funciones de distribución tiempo-frecuencia

Formulaciones

Existen varias formas diferentes de formular una función de distribución tiempo-frecuencia válida, lo que da como resultado varias distribuciones tiempo-frecuencia bien conocidas, como por ejemplo:

• Transformación de Fourier a corto plazo (incluyendo la transformación de Gabor),
• Wavelet transform,
• Función bilineal de distribución de tiempo-frecuencia (función de distribución Wigner, o WDF),
• Función de distribución de Wigner modificada, función de distribución de Gabor-Wigner, etc. (véase Gabor-Wigner transform).
• Hilbert-Huang transform

Puede encontrar más información sobre la historia y la motivación del desarrollo de la distribución tiempo-frecuencia en la entrada Representación tiempo-frecuencia.

Función de distribución TF ideal

Una función de distribución tiempo-frecuencia idealmente tiene las siguientes propiedades:

1. Alta resolución en tiempo y frecuencia, para facilitar el análisis e interpretación.
2. No a corto plazo para evitar confundir componentes reales de artefactos o ruido.
3. Una lista de propiedades matemáticas deseables para garantizar que esos métodos beneficien la aplicación de la vida real.
4. Baja complejidad computacional para garantizar el tiempo necesario para representar y procesar una señal en un plano de frecuencia-tiempo permite las implementaciones en tiempo real.

A continuación se muestra una breve comparación de algunas funciones de distribución de tiempo-frecuencia seleccionadas.

Para analizar bien las señales, es importante elegir una función de distribución tiempo-frecuencia adecuada. La función de distribución de tiempo-frecuencia que se debe utilizar depende de la aplicación que se esté considerando, como se muestra al revisar una lista de aplicaciones. La alta claridad de la función de distribución de Wigner (WDF) obtenida para algunas señales se debe a la función de autocorrelación inherente a su formulación; sin embargo, esto último también causa el problema entre términos. Por lo tanto, si queremos analizar una señal de un solo término, usar el WDF puede ser el mejor enfoque; Si la señal se compone de múltiples componentes, algunos otros métodos como la transformada de Gabor, la distribución de Gabor-Wigner o las funciones de distribución B modificada pueden ser mejores opciones.

A modo de ilustración, las magnitudes del análisis de Fourier no localizado no pueden distinguir las señales:

${\displaystyle x_{1}(t)={\begin{cases}\cos(\pi t); correspondió10\\cos(3\s(3\pi t); tercero10\leq t made20\\cos(2\pi t); limite {\20\end{cases}}}}}$

${\displaystyle x_{2}(t)={\begin{cases}\cos(\pi t); correspondió10\\cos(2\pi t); tercero10\leq t won20\cos(3\pi t); limite confianza20\end{cases}}}}}$

Pero el análisis de frecuencias puede.

Análisis de TF y procesos aleatorios

Para un proceso aleatorio x(t), no podemos encontrar el valor explícito de x(t).

El valor de x(t) se expresa como una función de probabilidad.

Procesos aleatorios generales

• Función de covariancia automática (ACF) ${\displaystyle R_{x}(t,\tau)}$

${\displaystyle R_{x}(t,\tau)=E[x(t+\tau /2)x^{*}(t-\tau /2)}}$

En lo habitual, suponemos que ${\displaystyle E[x(t)]=0}$ para cualquier t,

${\displaystyle E[x(t+\tau /2)x^{*}(t-\tau /2)}$

${\displaystyle =\iint x(t+\tau /2,\xi _{1})x^{*}(t-\tau /2,\xi _{2})P(\xi _{1},\xi _{2})d\xi _{1}d\xi ¿Qué?$

(Definición alternativa de la función de autocovariancia)

${\fnMicrosoft Sans Serif}(t,\tau)=E[x(t)x(t+\tau)}$

• Densidad espectral de potencia (PSD) ${\displaystyle S_{x}(t,f)}$

${\displaystyle S_{x}(t,f)=\int _{-\infty }R_{x}(t,\tau)e^{-j2\pi f\tau }d\tau }$

• Relación entre el WDF (Función de Distribución de Wigner) y el PSD

${\displaystyle E[W_{x}(t,f)]=\int _{-\infty }E[x(t+\tau /2)x^{*}(t-\tau /2)]\cdot e^{-j2\ f\tau }\cdot d\tau }$

${\displaystyle =\int _{-\infty }R_{x}(t,\tau)\cdot e^{-j2\pi f\tau }\cdot d\tau }$${\displaystyle =S_{x}(t,f)}$

• Relación entre la función de ambigüedad y la ACF

${\displaystyle E[A_{X}(\eta\tau)]=\int _{-\infty }{\infty }E[x(t+\tau /2)x^{*}(t-\tau /2)]e^{-j2\pi t\eta }dt}$

${\displaystyle =\int _{-\infty }R_{x}(t,\tau)e^{-j2\pi t\eta }dt}$

Procesos aleatorios estacionarios

• Proceso aleatorio estacionario: las propiedades estadísticas no cambian con t. Su función de autocovariancia:

${\displaystyle R_{x}(t_{1},\tau)=R_{x}(t_{2},\tau)=R_{x}(\tau)}$ para cualquier ${\displaystyle t}$Por lo tanto, ${\displaystyle R_{x}(\tau)=E[x(\tau /2)x^{*}(-\tau /2)}$${\displaystyle =\iint x(\tau /2,\xi _{1})x^{*}(-\tau /2,\xi _{2})P(\xi _{1},\xi _{2})d\xi _{1}d\xi ¿Qué?$PSD, ${\displaystyle S_{x}(f)=\int ¿Por qué?$ Ruido blanco:

${\displaystyle S_{x}(f)=\sigma }$ Donde ${\displaystyle \sigma }$ es algo constante.

• Cuando x(t) es estacionario,

${\displaystyle E[W_{x}(t,f)]=S_{x}(f)}$ (invariante con ${\displaystyle t}$)

${\displaystyle E[A_{x}(\eta\tau)]=\int _{-\infty }^{\infty }R_{x}(\tau)\cdot e^{-j2\pi t\eta }\cdot dt}$${\displaystyle =R_{x}(\tau)\int ¿Por qué? }\cdot dt}$${\displaystyle =R_{x}(\tau)\delta (\eta)}$ (nózero solamente cuando ${\displaystyle \eta =0}$)

Ruido blanco aditivo

• Para el ruido blanco aditivo (AWN),

${\displaystyle E[W_{g}(t,f)}=\sigma }$

${\displaystyle E[A_{x}(\eta\tau)]=\sigma \delta (\tau)\delta (\eta)}$

• Diseño de filtro para una señal en el ruido blanco aditivo

${\displaystyle E_{x}$: energía de la señal

${\displaystyle A}$: área de la distribución de frecuencia de tiempo de la señal

El PSD del ruido blanco es ${\displaystyle S_{n}(f)=\sigma }$

${\displaystyle SNR\approx 10\log _{10}{\frac {E_{x}{\iint \limits _{(t,f)\in {\text{signal part}}S_{x}(t,f)dtdf}}}}}}}$

${\displaystyle SNR\approx 10\log _{10}{\frac {E_{x}{\sigma \mathrm {A}}}$

Procesos aleatorios no estacionarios

• Si ${\displaystyle E[W_{x}(t,f)}$ varias con ${\displaystyle t}$ y ${\displaystyle E[A_{x}(\eta\tau)}$ no es cero cuando ${\displaystyle \eta =0}$Entonces ${\displaystyle x(t)}$ es un proceso aleatorio no estacionario.
• Si
  1. ${\displaystyle h(t)=x_{1}(t)+x_{2}(t)+x_{3}(t)+...+x_{k}(t)}$
  2. ${\displaystyle x_{n}(t)}$'s tienen cero significa para todos ${\displaystyle t}$'s
  3. ${\displaystyle x_{n}(t)}$'s son mutuamente independientes para todos ${\displaystyle t}$'s y ${\displaystyle \tau }$'s

entonces:

${\displaystyle E[x_{m}(t+\tau /2)x_{n}{*}(t-\tau /2)]=E[x_{m}(t+\tau /2)]E[x_{n}^{*}(t-\tau /2)]=0}$

• si ${\displaystyle m\neq n}$Entonces

${\displaystyle E[W_{h}(t,f)]=\sum ¿Qué?$

${\displaystyle E[A_{h}(\eta\tau)]=\sum _{n=1}E[A_{x_{n} {\eta\tau]}$

Transformada de Fourier de corto tiempo

• Proceso aleatorio para STFT (Short Time Fourier Transform)

${\displaystyle E[x(t)]\neq 0}$ Debería estar satisfecho. De lo contrario, ${\displaystyle E[X(t,f)]=E[\int ¿Por qué?$${\displaystyle =\int ¿Por qué?$para el proceso aleatorio de cero medios, ${\displaystyle E[X(t,f)]=0}$

• Descompuesto por la AF y la FRFT. Cualquier proceso aleatorio no estacionario se puede expresar como una suma de la transformación fraccional Fourier (o multiplicación de chirp) del proceso aleatorio estacionario.

Aplicaciones

Las siguientes aplicaciones necesitan no sólo las funciones de distribución de tiempo-frecuencia sino también algunas operaciones con la señal. La transformada canónica lineal (LCT) es realmente útil. Mediante LCT, la forma y ubicación en el plano tiempo-frecuencia de una señal puede tener la forma arbitraria que queramos. Por ejemplo, los LCT pueden cambiar la distribución tiempo-frecuencia a cualquier ubicación, dilatarla en dirección horizontal y vertical sin cambiar su área en el plano, cortarla (o torcerla) y rotarla (transformada fraccionaria de Fourier). Esta poderosa operación, LCT, hace que sea más flexible analizar y aplicar las distribuciones tiempo-frecuencia.

Estimación instantánea de frecuencia

La definición de frecuencia instantánea es la tasa de cambio de fase en el tiempo, o

${\displaystyle {\frac}{2\pi} }{\frac {d} {dt}\phi (t),}$

Donde ${\displaystyle \phi (t)}$ es la fase instantánea de una señal. Podemos conocer la frecuencia instantánea desde el plano de frecuencia-tiempo directamente si la imagen es lo suficientemente clara. Debido a que la alta claridad es crítica, a menudo utilizamos WDF para analizarla.

Filtro TF y descomposición de señal

El objetivo del diseño del filtro es eliminar el componente no deseado de una señal. Convencionalmente, podemos filtrar en el dominio del tiempo o en el dominio de frecuencia individualmente como se muestra a continuación.

Los métodos de filtrado mencionados anteriormente no pueden funcionar bien para todas las señales que pueden superponerse en el dominio del tiempo o en el dominio de la frecuencia. Al utilizar la función de distribución tiempo-frecuencia, podemos filtrar en el dominio euclidiano de tiempo-frecuencia o en el dominio fraccionario empleando la transformada fraccionaria de Fourier. A continuación se muestra un ejemplo.

El diseño de filtros en el análisis de tiempo-frecuencia siempre trata con señales compuestas de múltiples componentes, por lo que no se puede utilizar WDF debido a los términos cruzados. La transformada de Gabor, la función de distribución de Gabor-Wigner o la función de distribución de clases de Cohen pueden ser mejores opciones.

El concepto de descomposición de señal se refiere a la necesidad de separar un componente de los demás en una señal; esto se puede lograr mediante una operación de filtrado que requiere una etapa de diseño de filtro. Este filtrado se hace tradicionalmente en el dominio del tiempo o en el dominio de frecuencia; sin embargo, esto no puede ser posible en el caso de señales no estacionarias que son multicomponentes ya que tales componentes podrían superponerse tanto en el dominio del tiempo como en el dominio de frecuencia; como consecuencia, la única manera posible de lograr la separación de componentes y por lo tanto una descomposición de señal es implementar un filtro de frecuencia-tiempo.

Teoría de muestreo

Según el teorema de muestreo de Nyquist-Shannon, podemos concluir que el número mínimo de puntos de muestreo sin alias es equivalente al área de la distribución tiempo-frecuencia de una señal. (En realidad, esto es solo una aproximación, porque el área TF de cualquier señal es infinita). A continuación se muestra un ejemplo antes y después de combinar la teoría de muestreo con la distribución tiempo-frecuencia:

Es notable que el número de puntos de muestreo disminuye después de aplicar la distribución tiempo-frecuencia.

Cuando usamos WDF, puede haber un problema de términos cruzados (también llamado interferencia). Por otro lado, el uso de la transformada de Gabor provoca una mejora en la claridad y legibilidad de la representación, mejorando así su interpretación y aplicación a problemas prácticos.

En consecuencia, cuando la señal que tendemos a muestrear está compuesta de un solo componente, utilizamos el WDF; sin embargo, si la señal consta de más de un componente, el uso de la transformada de Gabor, la función de distribución de Gabor-Wigner u otros TFD de interferencia reducida pueden lograr mejores resultados.

El teorema de Balian-Low formaliza esto y proporciona un límite al número mínimo de muestras de tiempo-frecuencia necesarias.

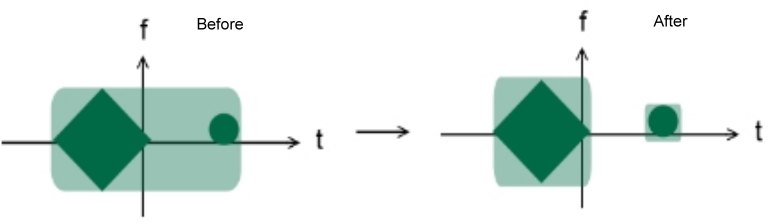
Modulación y multiplexación

Convencionalmente, el funcionamiento de concentrados de modulación y multiplexación en tiempo o en frecuencia, por separado. Aprovechando la distribución de tiempo-frecuencia, podemos hacer que sea más eficiente modular y multiplex. Todo lo que tenemos que hacer es llenar el avión de frecuencia. Presentamos un ejemplo como a continuación.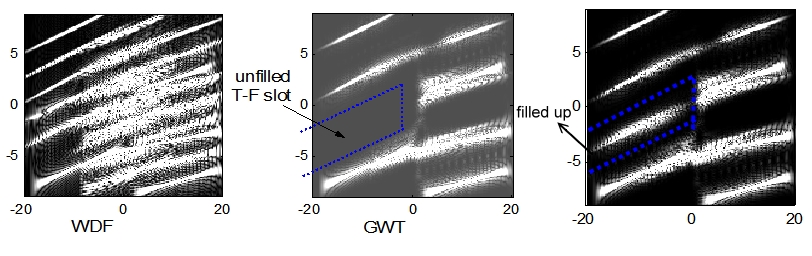

Como se ilustra en el ejemplo superior, usar WDF no es inteligente ya que el grave problema de términos cruzados dificulta la multiplexación y la modulación.

Propagación de ondas electromagnéticas

Podemos representar una onda electromagnética en forma de matriz de 2 por 1

${\displaystyle {\begin{bmatrix}x\y\end{bmatrix}}}$

que es similar al plano tiempo-frecuencia. Cuando una onda electromagnética se propaga a través del espacio libre, se produce la difracción de Fresnel. Podemos operar con la matriz 2 por 1.

${\displaystyle {\begin{bmatrix}x\y\end{bmatrix}}$

por LCT con matriz de parámetros

${\displaystyle {\begin{bmatrix}a limitadab\c limitadad\end{bmatrix}={\begin{bmatrix}1 limit\lambda .$

Donde z es la distancia de propagación y ${\displaystyle \lambda }$ es la longitud de onda. Cuando la onda electromagnética pasa a través de una lente esférica o se refleja en un disco, la matriz del parámetro debe ser

${\begin{\begin{bmatrix}a Pulb\\c\d\end{bmatrix}={\begin{bmatrix}1 limit0\-{\frac} {1}{\lambda f}} {1\end{bmatrix}}$

y

${\fnMicrosoft}={\begin{bmatrix}1 {\fnMicroc} {1}{\lambda R}} {1\end{bmatrix}}$

respectivamente, donde ƒ es la distancia focal de la lente y R es el radio del disco. Estos resultados correspondientes se pueden obtener de

${\displaystyle {\begin{bmatrix}a Pulb\c\d\end{bmatrix}{\begin{bmatrix}x\\\y\end{bmatrix}}} {\begin{bmatrix}} {\begin{bmatrix}$

Óptica, acústica y biomedicina

La luz es una onda electromagnética, por lo que el análisis de frecuencia-tiempo se aplica a la óptica de la misma manera que para la propagación general de ondas electromagnéticas.

De manera similar, es una característica de las señales acústicas que sus componentes de frecuencia sufren variaciones abruptas en el tiempo y, por lo tanto, no estarían bien representadas por un análisis de componente de frecuencia único que cubra todas sus duraciones.

Dado que las señales acústicas se utilizan como discurso en la comunicación entre el human-sender y -recibidor, su transmisión sin demora en los sistemas de comunicación técnica es crucial, lo que hace que el uso de TFDs más simples, como la transformación Gabor, adecuado para analizar estas señales en tiempo real reduciendo la complejidad computacional.

Si la velocidad de análisis de frecuencia no es una limitación, debe hacerse una comparación detallada de características con criterios bien definidos antes de seleccionar un TFD en particular. Otro enfoque es definir un TFD dependiente de señal que se adapte a los datos. En la biomedicina se puede utilizar la distribución de frecuencias temporales para analizar la electromiografía (EMG), electroencefalografía (EEG), electrocardiograma (ECG) o emisiones otoacústicas (OAEs).

Historia

Los primeros trabajos en análisis tiempo-frecuencia se pueden ver en las wavelets de Haar (1909) de Alfréd Haar, aunque no se aplicaron significativamente al procesamiento de señales. Dennis Gabor realizó trabajos más sustanciales, como los átomos de Gabor (1947), una forma temprana de wavelets, y la transformada de Gabor, una transformada de Fourier modificada de corto tiempo. La distribución Wigner-Ville (Ville 1948, en un contexto de procesamiento de señales) fue otro paso fundamental.

Particularmente en las décadas de 1930 y 1940, el análisis tiempo-frecuencia se desarrolló en conjunto con la mecánica cuántica (Wigner desarrolló la distribución Wigner-Ville en 1932 en mecánica cuántica, y Gabor fue influenciado por la mecánica cuántica; ver Átomo de Gabor); esto se refleja en las matemáticas compartidas del plano posición-momento y del plano tiempo-frecuencia, como en el principio de incertidumbre de Heisenberg (mecánica cuántica) y el límite de Gabor (análisis tiempo-frecuencia), que en última instancia reflejan ambos una estructura simpléctica.

Una de las primeras motivaciones prácticas para el análisis tiempo-frecuencia fue el desarrollo del radar (ver función de ambigüedad).