Análisis mecánico dinámico

El análisis mecánico dinámico (abreviado DMA) es una técnica utilizada para estudiar y caracterizar materiales. Es más útil para estudiar el comportamiento viscoelástico de los polímeros. Se aplica una tensión sinusoidal y se mide la tensión en el material, lo que permite determinar el módulo complejo. La temperatura de la muestra o la frecuencia del estrés a menudo varían, lo que lleva a variaciones en el módulo complejo; este enfoque se puede utilizar para localizar la temperatura de transición vítrea del material, así como para identificar las transiciones correspondientes a otros movimientos moleculares.

Teoría

Propiedades viscoelásticas de los materiales

Figura 1. Un probador DMA típico con empuñaduras para mantener la muestra y la cámara ambiental para proporcionar diferentes condiciones de temperatura. Una muestra se monta sobre las agarres y la cámara ambiental puede deslizarse hacia arriba para adjuntar la muestra.

Los polímeros compuestos por cadenas moleculares largas tienen propiedades viscoelásticas únicas, que combinan las características de los sólidos elásticos y los fluidos newtonianos. La teoría clásica de la elasticidad describe las propiedades mecánicas del sólido elástico donde el estrés es proporcional a la deformación en pequeñas deformaciones. Tal respuesta de estrés es independiente de la velocidad de deformación. La teoría clásica de la hidrodinámica describe las propiedades de los fluidos viscosos, para los cuales la respuesta de la tensión depende de la velocidad de deformación. Este comportamiento sólido y líquido de los polímeros se puede modelar mecánicamente con combinaciones de resortes y amortiguadores.

Módulos dinámicos de polímeros

La propiedad viscoelástica de un polímero se estudia mediante un análisis mecánico dinámico en el que se aplica una fuerza sinusoidal (tensión σ) a un material y se mide el desplazamiento resultante (deformación). Para un sólido perfectamente elástico, la deformación resultante y la tensión estarán perfectamente en fase. Para un fluido puramente viscoso, habrá un desfase de deformación de 90 grados con respecto a la tensión. Los polímeros viscoelásticos tienen características intermedias en las que se producirá algún retraso de fase durante las pruebas de DMA. Cuando se aplica la tensión y la tensión se retrasa, se cumplen las siguientes ecuaciones:

• Estrés: σ σ =σ σ 0pecado⁡ ⁡ ()t⋅ ⋅ +δ δ ){displaystyle sigma =sigma _{0}sin(tomega +delta),}
• Strain: ε ε =ε ε 0pecado⁡ ⁡ ()t⋅ ⋅ ){displaystyle varepsilon =varepsilon _{0}sin(tomega)}

dónde

⋅ ⋅ {displaystyle omega } es frecuencia de oscilación de la tensión,

t{displaystyle t} es tiempo,

δ δ {displaystyle delta } es el retraso de fase entre estrés y tensión.

Considere el caso puramente elástico, donde el estrés es proporcional a la tensión dada por el módulo de Young E{displaystyle E}. Tenemos
σ σ ()t)=Eε ε ()t)⟹ ⟹ σ σ 0pecado⁡ ⁡ ()⋅ ⋅ t+δ δ )=Eε ε 0pecado⁡ ⁡ ⋅ ⋅ t⟹ ⟹ δ δ =0{displaystyle sigma (t)=Eepsilon (t)implies sigma _{0}sin {(omega t+delta)}=Eepsilon ####sin {omega t}implies delta =0}

Ahora para el caso puramente viscoso, donde el estrés es proporcional a la tensión Tasa.
σ σ ()t)=Kdε ε dt⟹ ⟹ σ σ 0pecado⁡ ⁡ ()⋅ ⋅ t+δ δ )=Kε ε 0⋅ ⋅ #⁡ ⁡ ⋅ ⋅ t⟹ ⟹ δ δ =π π 2{displaystyle sigma (t)=K{frac {depsilon }{dt}implies sigma _{0}sin {(omega t+delta)}=Kepsilon {0}omega cos {omega t}implies delta ={frac {pi} } {2}}

El módulo de almacenamiento mide la energía almacenada, que representa la porción elástica, y el módulo de pérdida mide la energía disipada como calor, que representa la porción viscosa. Los módulos de almacenamiento y pérdida por tracción se definen de la siguiente manera:

• Modulo de almacenamiento: E.=σ σ 0ε ε 0#⁡ ⁡ δ δ {displaystyle E'={frac {sigma ¿Qué? ¿Por qué?
• Modulo de pérdida: E.=σ σ 0ε ε 0pecado⁡ ⁡ δ δ {displaystyle E'={frac {sigma ¿Qué? Sin delta
• Ángulo de fase: δ δ =arctan⁡ ⁡ E.E.{displaystyle delta =arctan {frac {E'} {E'}}

Del mismo modo, en el esquilamiento en lugar del caso de tensión, también definimos los módulos de almacenamiento y pérdida, G.{displaystyle G. y G.{displaystyle G'}.

Las variables complejas se pueden utilizar para expresar el moduli EAlternativa Alternativa {displaystyle E^{*} y GAlternativa Alternativa {displaystyle G^{*} como sigue:

EAlternativa Alternativa =E.+iE.=σ σ 0ε ε 0eiδ δ {displaystyle E^{*}=E'+iE'={frac {sigma ¿Qué? ¿Qué?

GAlternativa Alternativa =G.+iG.{displaystyle G^{*}=G'+iG',}

dónde

i2=− − 1{displaystyle {i}{2}=-1,}

Derivación de módulos dinámicos

Estrés σ σ ()t)=∫ ∫ − − JUEGO JUEGO tG()t− − t.)γ γ Í Í ()t.)dt.{displaystyle sigma (t)=int _{-infty }G(t-t'){dot {gamma }(t'dt'} de un elemento finito en una dirección se puede expresar con módulo de relajación G()t− − t.){displaystyle G(t-t)} y tasa de tensión, integrada en todos los tiempos pasados t.{displaystyle t} hasta el momento actual t{displaystyle t}. Con tasa de tensión γ γ ()t)Í Í =⋅ ⋅ ⋅ ⋅ γ γ 0⋅ ⋅ #⁡ ⁡ ()⋅ ⋅ t){displaystyle {dot {gamma (t)}=omega cdot gamma _{0}cdot cos(omega t)}y sustitución .. ()t.)=t− − t.=s{displaystyle xi (t')=t-t=s} uno obtiene σ σ ()t)=∫ ∫ .. ()− − JUEGO JUEGO )=t− − ()− − JUEGO JUEGO ).. ()t)=t− − tG()s)⋅ ⋅ γ γ 0⋅ ⋅ #⁡ ⁡ ()⋅ ⋅ ()t− − s))()− − ds)=γ γ 0∫ ∫ 0JUEGO JUEGO ⋅ ⋅ G()s)#⁡ ⁡ ()⋅ ⋅ ()t− − s))ds{infty)== {infty)=t-(-infty)}^{xi (t)=t-t}G(s)omega gamma _{0}cdot cos(omegads)=gamma _{0} {0}cdotcdot}. Aplicación del teorema de adición trigonométrica #⁡ ⁡ ()x± ± Sí.)=#⁡ ⁡ ()x)#⁡ ⁡ ()Sí.)∓ ∓ pecado⁡ ⁡ ()x)pecado⁡ ⁡ ()Sí.){displaystyle cos(xpm y)=cos(x)cos(y)mp sin(x)sin(y)} conducir a la expresión

σ σ ()t)γ γ ()t)=[⋅ ⋅ ∫ ∫ oJUEGO JUEGO G()s)pecado⁡ ⁡ ()⋅ ⋅ s)ds]⏟ ⏟ módulo de almacenamientoG.pecado⁡ ⁡ ()⋅ ⋅ t)+[⋅ ⋅ ∫ ∫ oJUEGO JUEGO G()s)#⁡ ⁡ ()⋅ ⋅ s)ds]⏟ ⏟ shear loss modulusG.#⁡ ⁡ ()⋅ ⋅ t).{displaystyle {frac {sigma (t)}{gamma (t)}=underbrace {[omega int _{o}infty }G(s)sin(omega s)ds]} _{text{shear storage modulus }G'}sin(omega t)+underbrace {[omega int _{o}^{infty }G(s)cos(omega s)ds]} ¿Por qué?

con integrales convergentes, si G()s)→ → 0{displaystyle G(s)rightarrow 0} para s→ → JUEGO JUEGO {displaystyle srightarrow infty}, que dependen de la frecuencia pero no del tiempo. Prórroga σ σ ()t)=σ σ 0⋅ ⋅ pecado⁡ ⁡ ()⋅ ⋅ ⋅ ⋅ t+Δ Δ φ φ ){displaystyle sigma (t)=sigma _{0}cdot sin(omega cdot t+Delta varphi)} con identidad trigonométrica pecado⁡ ⁡ ()x± ± Sí.)=pecado⁡ ⁡ ()x)⋅ ⋅ #⁡ ⁡ ()Sí.)± ± #⁡ ⁡ ()x)⋅ ⋅ pecado⁡ ⁡ ()Sí.){displaystyle sin(xpm y)=sin(x)cdot cos(y)pm cos(x)cdot sin(y)} plomo

σ σ ()t)γ γ ()t)=σ σ 0γ γ 0⋅ ⋅ #⁡ ⁡ ()Δ Δ φ φ )⏟ ⏟ G.⋅ ⋅ pecado⁡ ⁡ ()⋅ ⋅ ⋅ ⋅ t)+σ σ 0γ γ 0⋅ ⋅ pecado⁡ ⁡ ()Δ Δ φ φ )⏟ ⏟ G.⋅ ⋅ #⁡ ⁡ ()⋅ ⋅ ⋅ ⋅ t){displaystyle {frac {sigma (t)}{gamma (t)}=underbrace {frac {sigma ¿Por qué? ¿Por qué? _{G'}cdot sin(omega cdot t)+underbrace {{frac {sigma ¿Por qué? ¿Qué? ¿Por qué?.

Comparación de los dos σ σ ()t)γ γ ()t){displaystyle {frac {sigma (t)}{gamma (t)}}} ecuaciones conducen a la definición de G.{displaystyle G. y G.{displaystyle G'}.

Aplicaciones

Medición de la temperatura de transición vítrea

Una aplicación importante de DMA es la medición de la temperatura de transición vítrea de los polímeros. Los polímeros amorfos tienen diferentes temperaturas de transición vítrea, por encima de las cuales el material tendrá propiedades gomosas en lugar de un comportamiento vítreo y la rigidez del material se reducirá drásticamente junto con una reducción de su viscosidad. En la transición vítrea, el módulo de almacenamiento disminuye drásticamente y el módulo de pérdida alcanza un máximo. El DMA de barrido de temperatura se usa a menudo para caracterizar la temperatura de transición vítrea de un material.

Gráfico 2. Termograma DMA típico de un termoplástico amorfo (policarbonato). Modulus de almacenamiento (E’) y Loss Modulus (E’) y Factor de pérdida tan(delta) se parcelan como función de temperatura. Se detectó la temperatura de transición de vidrio del policarbonato alrededor de 151°C (evaluación según ISO 6721-11)

Composición polimérica

La variación de la composición de los monómeros y la reticulación pueden agregar o cambiar la funcionalidad de un polímero que puede alterar los resultados obtenidos de DMA. Un ejemplo de tales cambios se puede ver mezclando monómero de etileno propileno dieno (EPDM) con caucho de estireno-butadieno (SBR) y diferentes sistemas de reticulación o curado. Nair et al. abrevia las mezclas como E₀S, E₂₀S, etc., donde E₀S es igual al porcentaje en peso de EPDM en la mezcla y S indica azufre como agente de curado.

Al aumentar la cantidad de SBR en la mezcla, disminuyó el módulo de almacenamiento debido a las interacciones intermoleculares e intramoleculares que pueden alterar el estado físico del polímero. Dentro de la región vítrea, EPDM muestra el módulo de almacenamiento más alto debido a interacciones intermoleculares más fuertes (SBR tiene más impedimento estérico que lo hace menos cristalino). En la región gomosa, SBR muestra el módulo de almacenamiento más alto como resultado de su capacidad para resistir el deslizamiento intermolecular.

En comparación con el azufre, el módulo de almacenamiento más alto ocurrió para las mezclas curadas con peróxido de dicumilo (DCP) debido a las fortalezas relativas de los enlaces C-C y C-S.

La incorporación de rellenos de refuerzo en las mezclas de polímeros también aumenta el módulo de almacenamiento a expensas de limitar la altura del pico de la tangente de pérdida.

DMA también se puede utilizar para evaluar eficazmente la miscibilidad de los polímeros. La mezcla E₄₀S tuvo una transición mucho más amplia con un hombro en lugar de una caída pronunciada en un gráfico de módulo de almacenamiento de proporciones de mezcla variables, lo que indica que hay áreas que no son homogéneas.

Instrumentación

Gráfico 3. Esquemática general de un instrumento DMA.

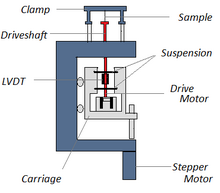
La instrumentación de un DMA consiste en un sensor de desplazamiento, como un transformador diferencial variable lineal, que mide un cambio en el voltaje como resultado del movimiento de la sonda del instrumento a través de un núcleo magnético, un sistema de control de temperatura u horno, un motor impulsor (un motor lineal para la carga de la sonda que proporciona carga para la fuerza aplicada), un sistema de guía y soporte del eje impulsor para actuar como una guía para la fuerza del motor a la muestra, y abrazaderas de muestra para sujetar la muestra que se está analizando. Dependiendo de lo que se esté midiendo, las muestras se prepararán y manejarán de manera diferente. En la figura 3 se muestra un esquema general de los componentes principales de un instrumento DMA.

Tipos de analizadores

Hay dos tipos principales de analizadores DMA utilizados actualmente: analizadores de resonancia forzada y analizadores de resonancia libre. Los analizadores de resonancia libre miden las oscilaciones libres de amortiguamiento de la muestra que se está probando suspendiendo y balanceando la muestra. Una restricción para los analizadores de resonancia libre es que se limita a muestras con forma de barra o rectangular, pero también se aplican muestras que se pueden tejer/trenzar. Los analizadores de resonancia forzada son el tipo más común de analizadores disponibles en la instrumentación actual. Estos tipos de analizadores obligan a la muestra a oscilar a una determinada frecuencia y son fiables para realizar un barrido de temperatura.

Gráfico 4. Mociones torsionales versus axiales.

Los analizadores se fabrican tanto para el control de la tensión (fuerza) como de la deformación (desplazamiento). En el control de deformación, la sonda se desplaza y la tensión resultante de la muestra se mide implementando un transductor de equilibrio de fuerza, que utiliza diferentes ejes. Las ventajas del control de la deformación incluyen una mejor respuesta a corto plazo para materiales de baja viscosidad y los experimentos de relajación de la tensión se realizan con relativa facilidad. En el control de tensión, se aplica una fuerza determinada a la muestra y se pueden variar varias otras condiciones experimentales (temperatura, frecuencia o tiempo). El control de tensión suele ser menos costoso que el control de tensión porque solo se necesita un eje, pero esto también hace que sea más difícil de usar. Algunas ventajas del control de la tensión incluyen el hecho de que es menos probable que se destruya la estructura de la muestra y que se pueden realizar con mucha más facilidad tiempos de relajación más largos/estudios de fluencia más largos. La caracterización de materiales de baja viscosidad tiene la desventaja de respuestas de corto tiempo que están limitadas por la inercia. Los analizadores de control de tensión y deformación brindan aproximadamente los mismos resultados siempre que la caracterización se encuentre dentro de la región lineal del polímero en cuestión. Sin embargo, el control de la tensión brinda una respuesta más realista porque los polímeros tienden a resistir una carga.

La tensión y la deformación se pueden aplicar a través de analizadores axiales o de torsión. Los analizadores de torsión se utilizan principalmente para líquidos o fundidos, pero también se pueden implementar para algunas muestras sólidas, ya que la fuerza se aplica en un movimiento de torsión. El instrumento puede realizar experimentos de recuperación de fluencia, tensión-relajación y tensión-deformación. Los analizadores axiales se utilizan para materiales sólidos o semisólidos. Puede realizar pruebas de flexión, tracción y compresión (incluso especímenes líquidos y de corte si lo desea). Estos analizadores pueden probar materiales de mayor módulo que los analizadores de torsión. El instrumento puede realizar estudios de análisis termomecánicos (TMA) además de los experimentos que pueden realizar los analizadores de torsión. La figura 4 muestra la diferencia general entre las dos aplicaciones de tensión y deformación.

El cambio de la geometría de la muestra y los accesorios pueden hacer que los analizadores de tensión y deformación sean prácticamente indiferentes entre sí, excepto en los extremos de las fases de la muestra, es decir, materiales realmente fluidos o rígidos. Las geometrías y accesorios comunes para los analizadores axiales incluyen flexión de tres y cuatro puntos, voladizos dobles y simples, placas paralelas y variantes, placas a granel, de extensión/tracción y de corte y sándwiches. Las geometrías y accesorios para analizadores de torsión consisten en placas paralelas, cono y placa, couette y viga y trenza de torsión. Para utilizar DMA para caracterizar materiales, se debe abordar el hecho de que pequeños cambios dimensionales también pueden conducir a grandes imprecisiones en ciertas pruebas. El calentamiento por inercia y cizallamiento puede afectar los resultados de los analizadores de resonancia forzada o libre, especialmente en muestras de fluidos.

Modos de prueba

Se pueden utilizar dos tipos principales de modos de prueba para probar las propiedades viscoelásticas de los polímeros: pruebas de barrido de temperatura y barrido de frecuencia. Un tercer modo de prueba, menos estudiado, es la prueba de esfuerzo-deformación dinámica.

Barrido de temperatura

Un método común de prueba consiste en medir el módulo complejo a baja frecuencia constante y variar la temperatura de la muestra. Un pico prominente en #⁡ ⁡ ()δ δ ){displaystyle tan(delta)} aparece a la temperatura de transición de vidrio del polímero. También se pueden observar transiciones secundarias, que pueden atribuirse a la activación dependiente de la temperatura de una amplia variedad de movimientos de cadena. En polímeros semicristalinos, se pueden observar transiciones separadas para las secciones cristalinas y amorfos. Del mismo modo, varias transiciones se encuentran a menudo en mezclas de polímero.

Por ejemplo, se estudiaron mezclas de policarbonato y poli(acrilonitrilo-butadieno-estireno) con la intención de desarrollar un material a base de policarbonato sin la tendencia del policarbonato a fallas por fragilidad. El DMA de barrido de temperatura de las mezclas mostró dos fuertes transiciones que coincidían con las temperaturas de transición vítrea de PC y PABS, de acuerdo con el hallazgo de que los dos polímeros eran inmiscibles.

Barrido de frecuencia

Figura 5. Una prueba de barrido de frecuencia en policarbonato bajo temperatura ambiente (25 °C). Modulus de almacenamiento (E’) y Loss Modulus (E’) fueron trazados contra la frecuencia. Se observó el aumento de la frecuencia “congela” los movimientos de cadena y un comportamiento más rígido.

Una muestra se puede mantener a una temperatura fija y se puede probar a una frecuencia variable. Peaks in #⁡ ⁡ ()δ δ ){displaystyle tan(delta)} y en E’’ con respecto a la frecuencia se puede asociar con la transición de vidrio, que corresponde a la capacidad de las cadenas de moverse entre sí. Tenga en cuenta que esto implica que la transición de vidrio depende de la tasa de tensión además de la temperatura. También se pueden observar transiciones secundarias.

El modelo Maxwell proporciona una descripción conveniente, si no estrictamente exacta, de los materiales viscoselásticos. Aplicar un estrés sinusoidal a un modelo Maxwell da: E.=Eτ τ 0⋅ ⋅ τ τ 02⋅ ⋅ 2+1,{displaystyle E'={frac {Etau _{0}omega ♫ {tau ¿Qué? Donde τ τ 0=.. /E{displaystyle tau _{0}=eta /E} es el tiempo de relajación de Maxwell. Así, un pico en E’ se observa en la frecuencia 1/τ τ 0{displaystyle 1/tau _{0}. Un polímero real puede tener varios tiempos de relajación diferentes asociados con diferentes movimientos moleculares.

Estudios dinámicos de tensión-deformación

Al aumentar gradualmente la amplitud de las oscilaciones, se puede realizar una medición dinámica de tensión y deformación. La variación de los módulos de almacenamiento y pérdida con el aumento de la tensión se puede utilizar para la caracterización de materiales y para determinar el límite superior del régimen de tensión-deformación lineal del material.

Barrido combinado

Debido a que las transiciones vítreas y las transiciones secundarias se observan tanto en los estudios de frecuencia como en los estudios de temperatura, hay interés en los estudios multidimensionales, donde los barridos de temperatura se realizan a una variedad de frecuencias o los barridos de frecuencia se realizan a una variedad de temperaturas. Este tipo de estudio proporciona una rica caracterización del material y puede brindar información sobre la naturaleza del movimiento molecular responsable de la transición.

Por ejemplo, los estudios de poliestireno (T_g ≈110 °C) han observado una transición secundaria cerca de la temperatura ambiente. Los estudios de temperatura-frecuencia mostraron que la temperatura de transición es en gran medida independiente de la frecuencia, lo que sugiere que esta transición resulta del movimiento de un pequeño número de átomos; se ha sugerido que esto es el resultado de la rotación del grupo fenilo alrededor de la cadena principal.