Análisis exploratorio de datos

En estadística, el análisis exploratorio de datos (EDA) es un enfoque que consiste en analizar conjuntos de datos para resumir sus características principales, a menudo utilizando gráficos estadísticos y otros métodos de visualización de datos. Se puede utilizar un modelo estadístico o no, pero principalmente EDA sirve para ver qué nos pueden decir los datos más allá del modelado formal y, por lo tanto, contrasta las pruebas de hipótesis tradicionales. John Tukey ha promovido el análisis de datos exploratorios desde 1970 para alentar a los estadísticos a explorar los datos y posiblemente formular hipótesis que podrían conducir a nuevos experimentos y recopilación de datos. EDA es diferente del análisis de datos iniciales (IDA), que se centra más específicamente en verificar los supuestos necesarios para el ajuste del modelo y la prueba de hipótesis, y en manejar los valores faltantes y realizar transformaciones de variables según sea necesario. La EDA engloba a la IDA.

Descripción general

Tukey definió el análisis de datos en 1961 como: "Procedimientos para analizar datos, técnicas para interpretar los resultados de dichos procedimientos, formas de planificar la recopilación de datos para hacer su análisis más fácil, más preciso o más exacto, y todo la maquinaria y los resultados de las estadísticas (matemáticas) que se aplican al análisis de datos."

El análisis de datos exploratorio es una técnica de análisis para analizar e investigar el conjunto de datos y resume las principales características del conjunto de datos. La principal ventaja de EDA es proporcionar visualización de datos después de realizar el análisis. Este informe arrojará luz sobre la gestión organizacional con los diferentes factores como físicos, cognitivos y emocionales. Estos factores han sido juzgados por diferentes factores predictivos como la amenaza ambiental, la incapacidad para encontrar un respiro y la confianza afectiva y cognitiva. La defensa de EDA por parte de Tukey alentó el desarrollo de paquetes de computación estadística, especialmente S en Bell Labs. El lenguaje de programación S inspiró los sistemas S-PLUS y R. Esta familia de entornos de computación estadística presentaba capacidades de visualización dinámica enormemente mejoradas, lo que permitió a los estadísticos identificar valores atípicos, tendencias y patrones en los datos que merecían un estudio más detallado.

La EDA de Tukey estuvo relacionada con otros dos desarrollos en la teoría estadística: estadísticas robustas y estadísticas no paramétricas, las cuales intentaron reducir la sensibilidad de las inferencias estadísticas a los errores en la formulación de modelos estadísticos. Tukey promovió el uso de un resumen de cinco números de datos numéricos: los dos extremos (máximo y mínimo), la mediana y los cuartiles, porque esta mediana y los cuartiles, al ser funciones de la distribución empírica, están definidos para todas las distribuciones, a diferencia de la media y Desviación Estándar; Además, los cuartiles y la mediana son más robustos ante distribuciones asimétricas o de cola pesada que los resúmenes tradicionales (la media y la desviación estándar). Los paquetes S, S-PLUS y R incluían rutinas que utilizaban estadísticas de remuestreo, como Quenouille y Tukey's jackknife y Efron&#39.;s bootstrap, que no son paramétricos y robustos (para muchos problemas).

El análisis exploratorio de datos, las estadísticas sólidas, las estadísticas no paramétricas y el desarrollo de lenguajes de programación estadística facilitaron el trabajo de los estadísticos. Trabajar en problemas científicos y de ingeniería. Estos problemas incluían la fabricación de semiconductores y la comprensión de las redes de comunicaciones, que preocupaban a los Laboratorios Bell. Estos desarrollos estadísticos, todos defendidos por Tukey, fueron diseñados para complementar la teoría analítica de probar hipótesis estadísticas, particularmente el énfasis de la tradición laplaciana en las familias exponenciales.

Desarrollo

John W. Tukey escribió el libro Análisis de datos exploratorios en 1977. Tukey sostuvo que en estadística se ponía demasiado énfasis en las pruebas de hipótesis estadísticas (análisis de datos confirmatorios); era necesario poner más énfasis en el uso de datos para sugerir hipótesis a probar. En particular, sostuvo que confundir los dos tipos de análisis y emplearlos en el mismo conjunto de datos puede conducir a un sesgo sistemático debido a los problemas inherentes a la prueba de hipótesis sugeridas por los datos.

Los objetivos de EDA son:

• Permitir descubrimientos inesperados en los datos
• Sugerir hipótesis sobre las causas de los fenómenos observados
• Evaluar los supuestos en que se basará la inferencia estadística
• Apoyar la selección de instrumentos y técnicas estadísticos apropiados
• Proporcionar una base para una mayor recopilación de datos mediante encuestas o experimentos

Se han adoptado muchas técnicas EDA en la minería de datos. También se están enseñando a estudiantes jóvenes como una forma de introducirlos en el pensamiento estadístico.

Técnicas y herramientas

Hay una serie de herramientas que son útiles para EDA, pero EDA se caracteriza más por la actitud adoptada que por técnicas particulares.

Las técnicas gráficas típicas utilizadas en EDA son:

• Parcela de caja
• Histograma
• Gráfico multivario
• Gráfico de ejecución
• Gráfico de Pareto
• Scatter plot (2D/3D)
• Parcela de vapor y hoja
• Coordenadas paralelas
• Tasa de probabilidades
• Objetivo de la búsqueda de proyección
• Mapa de calor
• Gráfico de barras
• Gráfico horizontal
• Métodos de visualización basados en glifos tales como rostros de FenoPlot y Chernoff
• Métodos de proyección como la gran gira, tour guiado y tour manual
• Versiones interactivas de estas parcelas

Reducción de dimensionalidad:

• Escalada multidimensional
• Análisis principal de los componentes (ACP)
• PCA multilinear
• Reducción de la dimensión no lineal (NLDR)
• Iconografía de correlaciones

Las técnicas cuantitativas típicas son:

• Esmalte mediano
• Trimean
• Ordination

Historia

Muchas ideas de EDA se remontan a autores anteriores, por ejemplo:

• Francis Galton destacó estadísticas de pedidos y quantiles.
• Arthur Lyon Bowley utilizó precursores del tallo y un resumen de cinco números (Bowley utilizó realmente un "séptimo resumen", incluyendo los extremos, deciles y cuartiles, junto con la mediana—ver su Elementary Manual of Statistics (3rd edn., 1920), p. 62– define "el máximo y mínimo, mediana, cuartiles y dos deciles" como las "siete posiciones").
• Andrew Ehrenberg articula una filosofía de reducción de datos (ver su libro del mismo nombre).

El curso Estadística en la sociedad de la Open University (MDST 242) tomó las ideas anteriores y las fusionó con el trabajo de Gottfried Noether, que introdujo la inferencia estadística mediante el lanzamiento de monedas y la prueba de la mediana..

Ejemplo

Los hallazgos de EDA son ortogonales a la tarea de análisis principal. Para ilustrar, consideremos un ejemplo de Cook et al. donde la tarea de análisis es encontrar las variables que mejor predicen la propina que una cena le dará al camarero. Las variables disponibles en los datos recopilados para esta tarea son: el monto de la propina, la factura total, el sexo del pagador, la sección de fumadores/no fumadores, la hora del día, el día de la semana y el tamaño del grupo. La tarea de análisis principal se aborda ajustando un modelo de regresión donde la tasa de propinas es la variable de respuesta. El modelo ajustado es

(título) = 0.18 - 0.01 × (tamaño de las partes)

que dice que a medida que el tamaño del grupo de cena aumenta en una persona (lo que genera una factura más alta), la tasa de propina disminuirá en un 1%, en promedio.

Sin embargo, la exploración de los datos revela otras características interesantes no descritas por este modelo.

• 

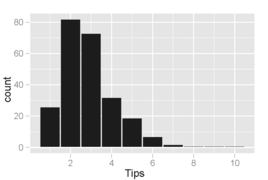
  Histograma de cantidades de punta donde los contenedores cubren $1 aumentos. La distribución de valores es correcta y unimodal, como es común en las distribuciones de pequeñas cantidades no negativas.

• 

  Histograma de las cantidades de punta donde los contenedores cubren $0.10 aumentos. Un fenómeno interesante es visible: los picos ocurren en las cantidades enteras de dólar y medio dólar, que es causada por los clientes que recogen números redondos como puntas. Este comportamiento es común a otros tipos de compras también, como la gasolina.

• 

  Scatterplot of tips vs. bill. Los puntos por debajo de la línea corresponden a puntas inferiores a lo esperado (para esa cantidad de factura), y los puntos por encima de la línea son más altos de lo esperado. Podríamos esperar ver una asociación lineal estrecha y positiva, pero en cambio ver la variación que aumenta con la cantidad de propina. En particular, hay más puntos lejos de la línea en la derecha inferior que en la izquierda superior, indicando que más clientes son muy baratos que muy generosos.

• 

  Escatterplot of tips vs. bill separated by payer gender and smoking section status. Fumar fiestas tienen mucho más variabilidad en los consejos que dan. Los hombres tienden a pagar las facturas superiores (muy) y las mujeres no fumadores tienden a ser propinas muy consistentes (con tres excepciones visibles mostradas en la muestra).

Lo que se aprende de los gráficos es diferente de lo que ilustra el modelo de regresión, aunque el experimento no fue diseñado para investigar ninguna de estas otras tendencias. Los patrones encontrados al explorar los datos sugieren hipótesis sobre la inclinación que tal vez no se hayan anticipado de antemano y que podrían conducir a interesantes experimentos de seguimiento en los que las hipótesis se plantean y prueban formalmente mediante la recopilación de nuevos datos.

Software

• JMP, un paquete de EDA del Instituto SAS.
• KNIME, Konstanz Information Miner – Open-Source data exploration platform based on Eclipse.
• Minitab, un paquete de EDA y estadísticas generales ampliamente utilizado en entornos industriales y corporativos.
• Orange, una suite de software de minería de datos de código abierto y aprendizaje automático.
• Python, un lenguaje de programación de código abierto ampliamente utilizado en la minería de datos y el aprendizaje automático.
• R, un lenguaje de programación de código abierto para computación estadística y gráficos. Junto con Python uno de los idiomas más populares para la ciencia de datos.
• TinkerPlots un software EDA para estudiantes de primaria y secundaria superior.
• Weka un paquete de extracción de datos de código abierto que incluye herramientas de visualización y EDA como la búsqueda de proyección específica.