Análisis estructural
Análisis estructural es una rama de la mecánica de sólidos que utiliza modelos simplificados para sólidos como barras, vigas y cubiertas para la toma de decisiones de ingeniería. Su principal objetivo es determinar el efecto de las cargas sobre las estructuras físicas y sus componentes. A diferencia de la teoría de la elasticidad, los modelos utilizados en el análisis de estructuras suelen ser ecuaciones diferenciales en una variable espacial. Las estructuras sujetas a este tipo de análisis incluyen todas las que deben soportar cargas, como edificios, puentes, aeronaves y barcos. El análisis estructural utiliza ideas de la mecánica aplicada, la ciencia de los materiales y las matemáticas aplicadas para calcular las deformaciones, las fuerzas internas, las tensiones, las reacciones de soporte, la velocidad, las aceleraciones y la estabilidad de una estructura. Los resultados del análisis se utilizan para verificar la idoneidad de uso de una estructura, lo que a menudo excluye las pruebas físicas. El análisis estructural es, por lo tanto, una parte clave del diseño de ingeniería de estructuras.
Estructuras y cargas
En el contexto del análisis estructural, una estructura se refiere a un cuerpo o sistema de partes conectadas que se usa para soportar una carga. Ejemplos importantes relacionados con la ingeniería civil incluyen edificios, puentes y torres; y en otras ramas de la ingeniería, son importantes las estructuras de barcos y aeronaves, los tanques, los recipientes a presión, los sistemas mecánicos y las estructuras de soporte eléctrico. Para diseñar una estructura, un ingeniero debe tener en cuenta su seguridad, estética y capacidad de servicio, al mismo tiempo que considera las limitaciones económicas y ambientales. Otras ramas de la ingeniería trabajan en una amplia variedad de estructuras no edificables.
Clasificación de estructuras
Un sistema estructural es la combinación de elementos estructurales y sus materiales. Es importante para un ingeniero estructural poder clasificar una estructura por su forma o su función, reconociendo los diversos elementos que componen esa estructura. Los elementos estructurales que guían las fuerzas sistémicas a través de los materiales no son solo una biela, una armadura, una viga o una columna, sino también un cable, un arco, una cavidad o canal, e incluso un ángulo, una estructura superficial., o un marco.
Cargas
Una vez definidos los requisitos dimensionales de una estructura, es necesario determinar las cargas que debe soportar la estructura. El diseño estructural, por lo tanto, comienza con la especificación de las cargas que actúan sobre la estructura. La carga de diseño para una estructura a menudo se especifica en los códigos de construcción. Hay dos tipos de códigos: códigos generales de construcción y códigos de diseño, los ingenieros deben cumplir con todos los requisitos del código para que la estructura siga siendo confiable.
Hay dos tipos de cargas que la ingeniería de estructuras debe enfrentar en el diseño. El primer tipo de cargas son las cargas muertas que consisten en los pesos de los diversos miembros estructurales y los pesos de cualquier objeto que esté permanentemente unido a la estructura. Por ejemplo, columnas, vigas, vigas maestras, la losa del piso, techos, paredes, ventanas, plomería, accesorios eléctricos y otros accesorios varios. El segundo tipo de cargas son las cargas vivas que varían en su magnitud y ubicación. Hay muchos tipos diferentes de cargas vivas, como cargas de construcción, cargas de puentes de carreteras, cargas de puentes ferroviarios, cargas de impacto, cargas de viento, cargas de nieve, cargas sísmicas y otras cargas naturales.
Métodos analíticos
Para realizar un análisis preciso, un ingeniero estructural debe determinar información como las cargas estructurales, la geometría, las condiciones de soporte y las propiedades de los materiales. Los resultados de dicho análisis suelen incluir reacciones de apoyo, tensiones y desplazamientos. Esta información luego se compara con los criterios que indican las condiciones de falla. El análisis estructural avanzado puede examinar la respuesta dinámica, la estabilidad y el comportamiento no lineal. Hay tres enfoques para el análisis: el enfoque de la mecánica de los materiales (también conocido como resistencia de los materiales), el enfoque de la teoría de la elasticidad (que en realidad es un caso especial del campo más general de la mecánica continua) y el enfoque de elementos finitos. Los dos primeros hacen uso de formulaciones analíticas que aplican en su mayoría modelos elásticos lineales simples, lo que conduce a soluciones de forma cerrada y, a menudo, se pueden resolver a mano. El enfoque de elementos finitos es en realidad un método numérico para resolver ecuaciones diferenciales generadas por teorías de la mecánica, como la teoría de la elasticidad y la resistencia de los materiales. Sin embargo, el método de elementos finitos depende en gran medida de la capacidad de procesamiento de las computadoras y es más aplicable a estructuras de tamaño y complejidad arbitrarios.
Independientemente del enfoque, la formulación se basa en las mismas tres relaciones fundamentales: equilibrio, constitutivo y compatibilidad. Las soluciones son aproximadas cuando alguna de estas relaciones se cumple sólo aproximadamente, o sólo una aproximación a la realidad.
Limitaciones
Cada método tiene limitaciones notables. El método de mecánica de materiales se limita a elementos estructurales muy simples bajo condiciones de carga relativamente simples. Sin embargo, los elementos estructurales y las condiciones de carga permitidas son suficientes para resolver muchos problemas de ingeniería útiles. La teoría de la elasticidad permite la solución de elementos estructurales de geometría general bajo condiciones generales de carga, en principio. La solución analítica, sin embargo, se limita a casos relativamente simples. La solución de problemas de elasticidad también requiere la solución de un sistema de ecuaciones diferenciales parciales, que es considerablemente más exigente matemáticamente que la solución de problemas de mecánica de materiales, que requieren como máximo la solución de una ecuación diferencial ordinaria. El método de elementos finitos es quizás el más restrictivo y el más útil al mismo tiempo. Este método en sí se basa en otras teorías estructurales (como las otras dos discutidas aquí) para resolver ecuaciones. Sin embargo, en general hace posible resolver estas ecuaciones, incluso con geometría y condiciones de carga muy complejas, con la restricción de que siempre hay algún error numérico. El uso efectivo y confiable de este método requiere una sólida comprensión de sus limitaciones.
Métodos de resistencia de materiales (métodos clásicos)
El método de la mecánica de materiales, el más simple de los tres que se analizan aquí, está disponible para miembros estructurales simples sujetos a cargas específicas, como barras cargadas axialmente, vigas prismáticas en un estado de flexión pura y ejes circulares sujetos a torsión. Las soluciones pueden, bajo ciertas condiciones, superponerse usando el principio de superposición para analizar un miembro sometido a carga combinada. Existen soluciones para casos especiales para estructuras comunes, como recipientes a presión de paredes delgadas.
Para el análisis de sistemas completos, este enfoque se puede utilizar junto con la estática, dando lugar al método de las secciones y al método de las uniones para el análisis de armaduras, momento método de distribución para marcos rígidos pequeños, y pórtico y método voladizo para marcos rígidos grandes. Excepto por la distribución de momentos, que comenzó a utilizarse en la década de 1930, estos métodos se desarrollaron en sus formas actuales en la segunda mitad del siglo XIX. Todavía se utilizan para estructuras pequeñas y para el diseño preliminar de estructuras grandes.
Las soluciones se basan en la elasticidad infinitesimal isotrópica lineal y en la teoría de vigas de Euler-Bernoulli. En otras palabras, contienen las suposiciones (entre otras) de que los materiales en cuestión son elásticos, que la tensión está relacionada linealmente con la deformación, que el material (pero no la estructura) se comporta de manera idéntica independientemente de la dirección de la carga aplicada, que todas las deformaciones son pequeños, y que las vigas son largas en relación con su profundidad. Como ocurre con cualquier suposición simplificadora en ingeniería, cuanto más se aleja el modelo de la realidad, menos útil (y más peligroso) es el resultado.
Ejemplo
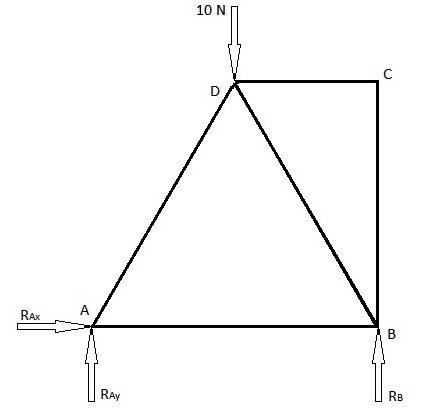
Hay 2 métodos comúnmente utilizados para encontrar las fuerzas de los elementos de la armadura, a saber, el método de los nudos y el método de las secciones. A continuación se muestra un ejemplo que se resuelve utilizando ambos métodos. El primer diagrama a continuación es el problema presentado para el cual se deben encontrar las fuerzas del elemento de armadura. El segundo diagrama es el diagrama de carga y contiene las fuerzas de reacción de las articulaciones.
Dado que hay una articulación de pasador en A, tendrá 2 fuerzas de reacción. Uno en la dirección x y el otro en la dirección y. En el punto B, hay una junta de rodillos y, por lo tanto, solo 1 fuerza de reacción en la dirección y. Suponiendo que estas fuerzas estén en sus respectivas direcciones positivas (si no están en las direcciones positivas, el valor será negativo).
Dado que el sistema está en equilibrio estático, la suma de fuerzas en cualquier dirección es cero y la suma de momentos alrededor de cualquier punto es cero. Por lo tanto, se puede calcular la magnitud y la dirección de las fuerzas de reacción.
- .. MA=0=− − 10Alternativa Alternativa 1+2Alternativa Alternativa RB⇒ ⇒ RB=5{displaystyle sum M_{A}=0=-10*1+2*R_{B}Rightarrow R_{B}=5}
- .. FSí.=0=RASí.+RB− − 10⇒ ⇒ RASí.=5{displaystyle sum F_{y}=0=R_{Ay}+R_{B}-10Rightarrow R_{Ay}=5}
- .. Fx=0=RAx{displaystyle sum F_{x}=0=R_{Ax}
Método de juntas
Este tipo de método utiliza el equilibrio de fuerzas en las direcciones x e y en cada uno de los nudos de la estructura de armadura.
En A,
- .. FSí.=0=RASí.+FADpecado ()60)=5+FAD32⇒ ⇒ FAD=− − 103{displaystyle sum F_{y}=0=R_{Ay}+F_{AD}sin(60)=5+F_{AD}{frac {sqrt {3}{2}f} Rightarrow F_{AD}=-{frac {10}{sqrt {}}}
- .. Fx=0=RAx+FAD# ()60)+FAB=0− − 10312+FAB⇒ ⇒ FAB=53{displaystyle sum F_{x}=0=R_{Ax}+F_{AD}cos(60)+F_{AB}=0-{frac {10}{sqrt {3}{frac} {1}{2}+F_{AB}Rightarrow F_{AB}={frac {5}{sqrt {}}}
En D,
- .. FSí.=0=− − 10− − FADpecado ()60)− − FBDpecado ()60)=− − 10− − ()− − 103)32− − FBD32⇒ ⇒ FBD=− − 103{displaystyle sum F_{y}=0=-10-F_{AD}sin(60)-F_{BD}sin(60)=-10-left(-{frac {10}{sqrt {3}right){frac {sqrt {3}{2}-F_{BD}{frac} {cHFF} {3}{2}f} Rightarrow F_{BD}=-{frac {10}{sqrt {}}}
- .. Fx=0=− − FAD# ()60)+FBD# ()60)+FCD=− − 10312+10312+FCD⇒ ⇒ FCD=0{displaystyle sum F_{x}=0=-F_{AD}cos(60)+F_{BD}cos(60)+F_{CD}=-{frac {10}{sqrt {3}{frac} {1}{2}}+{frac {10}{sqrt {3}{frac} {f} {f}} {f}}} {f}} {f}}} {f}}}} {f}} {f}}} {f} {f}}}} {f}}}} {f}}}}} {f}}}}}}} {f}}}}}} {f}f}}}}}}}}}}} {f} {f} {f} {f} {f} {f}}f}f}}}}}}}f}}}}f} {f} {f} {f} {f} {f} {f}f}f}f}f}f}f}f}f}}f}f}f}f}f}f}f}}}}f} {1}{2}+F_{CD}Rightarrow F_{CD}=0}
En C,
- .. FSí.=0=− − FBC⇒ ⇒ FBC=0{displaystyle sum F_{y}=0=-F_{BC}Rightarrow F_{BC}=0}
Aunque se encuentran las fuerzas en cada uno de los elementos de la armadura, es una buena práctica verificar los resultados completando los balances de fuerzas restantes.
- .. Fx=− − FCD=− − 0=0⇒ ⇒ verified{displaystyle sum F_{x }=-F_{CD}=-0=0Rightarrow verified}
En B,
- .. FSí.=RB+FBDpecado ()60)+FBC=5+()− − 103)32+0=0⇒ ⇒ verified{displaystyle sum F_{y}=R_{B}+F_{BD}sin(60)+F_{BC}=5+left(-{frac {10}{sqrt {3}}right){frac {sqrt}}}right){sqrt {3}{2}}+0=0Rightarrow verified}
- .. Fx=− − FAB− − FBD# ()60)=53− − 10312=0⇒ ⇒ verified{displaystyle sum F_{x }=-F_{AB}-F_{BD}cos(60)={frac {5} {fn} {fn} {fn} {fn} {fn} {fn} {fn}}}=0Rightarrow verified}
Método de secciones
Este método se puede utilizar cuando se encuentran las fuerzas del elemento de armadura de solo unos pocos miembros. Este método se utiliza introduciendo una sola línea recta que atraviesa el miembro cuya fuerza se debe calcular. Sin embargo, este método tiene un límite en el sentido de que la línea de corte puede pasar a través de un máximo de solo 3 miembros de la estructura de armadura. Esta restricción se debe a que este método utiliza los balances de fuerzas en la dirección x e y y el balance de momentos, lo que da un máximo de 3 ecuaciones para encontrar un máximo de 3 fuerzas desconocidas en los elementos de la armadura a través de los cuales se realiza este corte. Encuentre las fuerzas FAB, FBD y FCD en el ejemplo anterior
Método 1: ignorar el lado derecho

- .. MD=0=− − 5Alternativa Alternativa 1+3Alternativa Alternativa FAB⇒ ⇒ FAB=53{displaystyle sum M_{D}=0=-5*1+{sqrt {3}*F_{AB}Rightarrow F_{AB}={frac {5}{sqrt {}}}
- .. FSí.=0=RASí.− − FBDpecado ()60)− − 10=5− − FBD32− − 10⇒ ⇒ FBD=− − 103{displaystyle sum F_{y}=0=R_{Ay}-F_{BD}sin(60)-10=5-F_{BD}{frac {cHFF} {3}{2}-10f}Rightarrow F_{BD}=-{frac {10}{sqrt {}}}
- .. Fx=0=FAB+FBD# ()60)+FCD=53− − 10312+FCD⇒ ⇒ FCD=0{displaystyle sum F_{x}=0=F_{AB}+F_{BD}cos(60)+F_{CD}={frac {5}{sqrt {3}}-{frac {10}{sqrt {3}{frac} {1}{2}+F_{CD}Rightarrow F_{CD}=0}
Método 2: ignorar el lado izquierdo
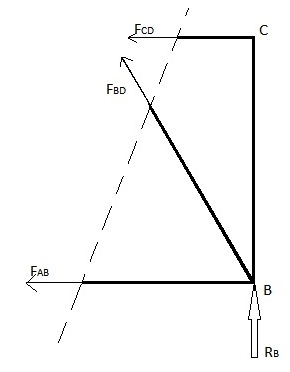
- .. MB=0=3Alternativa Alternativa FCD⇒ ⇒ FCD=0{displaystyle sum M_{B}=0={sqrt {3}*
- .. FSí.=0=FBDpecado ()60)+RB=FBD32+5⇒ ⇒ FBD=− − 103{displaystyle sum F_{y}=0=F_{BD}sin(60)+R_{B}=F_{BD}{frac {sqrt {3}{2}+5 Rightarrow F_{BD}=-{frac {10}{sqrt {}}}
- .. Fx=0=− − FAB− − FBD# ()60)− − FCD=− − FAB− − ()− − 103)12− − 0⇒ ⇒ FAB=53{displaystyle sum F_{x}=0=-F_{AB}-F_{BD}cos(60)-F_{CD}=-F_{AB}-left(-{frac {10}{sqrt {3}right){frac {1}{2}}-0Rightarrow F_{AB}={frac {5}{sqrt {}}}
Las fuerzas de los elementos de la armadura en los miembros restantes se pueden encontrar utilizando el método anterior con una sección que pasa por los miembros restantes.
Métodos de elasticidad
Los métodos de elasticidad generalmente están disponibles para un sólido elástico de cualquier forma. Se pueden modelar elementos individuales como vigas, columnas, fustes, placas y láminas. Las soluciones se derivan de las ecuaciones de elasticidad lineal. Las ecuaciones de elasticidad son un sistema de 15 ecuaciones diferenciales parciales. Debido a la naturaleza de las matemáticas involucradas, las soluciones analíticas solo se pueden producir para geometrías relativamente simples. Para geometrías complejas, es necesario un método de solución numérica como el método de elementos finitos.
Métodos que usan aproximación numérica
Es una práctica común utilizar soluciones aproximadas de ecuaciones diferenciales como base para el análisis estructural. Esto generalmente se hace usando técnicas de aproximación numérica. La aproximación numérica más utilizada en el análisis estructural es el método de elementos finitos.
El método de elementos finitos aproxima una estructura como un conjunto de elementos o componentes con varias formas de conexión entre ellos y cada elemento de los cuales tiene una rigidez asociada. Por lo tanto, un sistema continuo como una placa o capa se modela como un sistema discreto con un número finito de elementos interconectados en un número finito de nodos y la rigidez total es el resultado de la suma de la rigidez de los diversos elementos. El comportamiento de los elementos individuales se caracteriza por la relación de rigidez (o flexibilidad) del elemento. El ensamblaje de las diversas rigideces en una matriz maestra de rigidez que representa la estructura completa conduce a la relación de rigidez o flexibilidad del sistema. Para establecer la rigidez (o flexibilidad) de un elemento en particular, podemos usar el enfoque de mecánica de materiales para elementos de barra unidimensionales simples, y el enfoque de elasticidad para elementos más complejos. elementos bidimensionales y tridimensionales. El desarrollo analítico y computacional se realiza mejor a través del álgebra matricial, resolviendo ecuaciones diferenciales parciales.
Las primeras aplicaciones de los métodos matriciales se aplicaron a armazones articulados con elementos de armadura, viga y columna; Los métodos matriciales posteriores y más avanzados, denominados "análisis de elementos finitos", modelan una estructura completa con elementos de una, dos y tres dimensiones y se pueden utilizar para sistemas articulados junto con sistemas continuos como un recipiente a presión, placas, conchas y sólidos tridimensionales. El software informático comercial para el análisis estructural suele utilizar el análisis matricial de elementos finitos, que se puede clasificar en dos enfoques principales: el método de desplazamiento o rigidez y el método de fuerza o flexibilidad. El método de la rigidez es el más popular con diferencia gracias a su facilidad de implementación y formulación para aplicaciones avanzadas. La tecnología de elementos finitos ahora es lo suficientemente sofisticada como para manejar casi cualquier sistema, siempre que haya suficiente potencia informática disponible. Su aplicabilidad incluye, entre otros, análisis lineal y no lineal, interacciones sólidas y fluidas, materiales que son isótropos, ortótropos o anisótropos, y efectos externos que son factores ambientales, dinámicos y estáticos. Sin embargo, esto no implica que la solución calculada sea automáticamente confiable porque mucho depende del modelo y la confiabilidad de la entrada de datos.
Cronología
- 1452–1519 Leonardo da Vinci hizo muchas contribuciones
- 1638: Galileo Galilei publicó el libro "Dos nuevas ciencias" en el que examinó el fracaso de estructuras simples
- 1660: Ley de Hooke de Robert Hooke
- 1687: Isaac Newton publicó "Philosophiae Naturalis Principia Mathematica"que contiene las leyes del movimiento de Newton
- 1750: Ecuación del haz Euler–Bernoulli
- 1700–1782: Daniel Bernoulli introdujo el principio del trabajo virtual
- 1707-1783: Leonhard Euler desarrolló la teoría del balanceo de columnas
- 1826: Claude-Louis Navier publicó un tratado sobre los comportamientos elásticos de las estructuras
- 1873: Carlo Alberto Castigliano presentó su tesis "Intorno ai sistemi elastici", que contiene su teorema para el desplazamiento de la computación como derivado parcial de la energía de la cepa. Este teorema incluye el método de 'menos trabajo' como un caso especial
- 1878-1972 Stephen Timoshenko padre de la moderna mecánica aplicada incluyendo la teoría del rayo Timoshenko-Ehrenfest
- 1936: Hardy Cross' publicación del método de distribución de momento que fue posteriormente reconocido como una forma del método de relajación aplicable al problema del flujo en la red de tuberías
- 1941: Alexander Hrennikoff presentó su tesis D.Sc. en MIT sobre la discretización de problemas de elasticidad plana utilizando un marco de celo
- 1942: R. Courant dividió un dominio en subregiones finitas
- 1956: J. Turner, R. W. Clough, H. C. Martin y el documento de L. J. Topp sobre la "Stiffness and Deflection of Complex Structures" introduce el nombre "método de acabado" y es ampliamente reconocido como el primer tratamiento integral del método como se conoce hoy