Análisis discriminante lineal

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Método utilizado en estadísticas, reconocimiento de patrones y otros campos

Análisis discriminante lineal (LDA), análisis discriminante normal (NDA) o análisis discriminante El análisis de funciones es una generalización del discriminante lineal de Fisher, un método utilizado en estadística y otros campos, para encontrar una combinación lineal de características que caracteriza o separa dos o más clases de objetos o eventos. La combinación resultante se puede utilizar como clasificador lineal o, más comúnmente, para la reducción de dimensionalidad antes de una clasificación posterior.

LDA está estrechamente relacionado con el análisis de varianza (ANOVA) y el análisis de regresión, que también intentan expresar una variable dependiente como una combinación lineal de otras características o medidas. Sin embargo, ANOVA utiliza variables independientes categóricas y una variable dependiente continua, mientras que el análisis discriminante tiene variables independientes continuas y una variable dependiente categórica (es decir, la etiqueta de clase). La regresión logística y la regresión probit son más similares a LDA que ANOVA, ya que también explican una variable categórica mediante los valores de variables independientes continuas. Estos otros métodos son preferibles en aplicaciones donde no es razonable suponer que las variables independientes están distribuidas normalmente, lo cual es un supuesto fundamental del método LDA.

LDA también está estrechamente relacionado con el análisis de componentes principales (PCA) y el análisis factorial en el sentido de que ambos buscan combinaciones lineales de variables que expliquen mejor los datos. LDA intenta explícitamente modelar la diferencia entre las clases de datos. El PCA, por el contrario, no tiene en cuenta ninguna diferencia de clase y el análisis factorial construye las combinaciones de características basándose en diferencias más que en similitudes. El análisis discriminante también se diferencia del análisis factorial en que no es una técnica de interdependencia: se debe hacer una distinción entre variables independientes y variables dependientes (también llamadas variables de criterio).

LDA funciona cuando las mediciones realizadas sobre variables independientes para cada observación son cantidades continuas. Cuando se trata de variables independientes categóricas, la técnica equivalente es el análisis de correspondencia discriminante.

El análisis discriminante se utiliza cuando los grupos se conocen a priori (a diferencia del análisis de conglomerados). Cada caso debe tener una puntuación en una o más medidas predictivas cuantitativas y una puntuación en una medida grupal. En términos simples, el análisis de funciones discriminantes es clasificación: el acto de distribuir cosas en grupos, clases o categorías del mismo tipo.

Historia

El análisis discriminante dicotómico original fue desarrollado por Sir Ronald Fisher en 1936. Es diferente de un ANOVA o MANOVA, que se utiliza para predecir una (ANOVA) o múltiples (MANOVA) variables dependientes continuas mediante una o más variables categóricas independientes. . El análisis de funciones discriminantes es útil para determinar si un conjunto de variables es eficaz para predecir la pertenencia a una categoría.

LDA para dos clases

Considerar un conjunto de observaciones ${displaystyle {vec {x}}}$ (también llamadas características, atributos, variables o mediciones) para cada muestra de un objeto o evento con clase conocida ${displaystyle y}$ . Este conjunto de muestras se llama el conjunto de entrenamiento. El problema de clasificación es entonces encontrar un buen predictor para la clase ${displaystyle y}$ de cualquier muestra de la misma distribución (no necesariamente del conjunto de entrenamiento) ${displaystyle {vec {x}}}$ .

LDA aborda el problema asumiendo que las funciones de densidad de probabilidad condicional ${displaystyle p({vec {x}}|y=0)}$ y ${displaystyle p({vec {x}}|y=1)}$ son tanto la distribución normal con parámetros de media y covariancia ${displaystyle left({vec {mu }}_{0},Sigma _{0}right)}$ y ${displaystyle left({vec {mu }}_{1},Sigma _{1}right)}$ , respectivamente. Bajo esta suposición, la solución Bayes-optimal es predecir puntos como ser de la segunda clase si el registro de las ratios de probabilidad es más grande que un umbral T, por lo que:

T}" xmlns="http://www.w3.org/1998/Math/MathML">12()x→ → − − μ μ → → 0)T. . 0− − 1()x→ → − − μ μ → → 0)+12In⁡ ⁡ Silencio. . 0Silencio− − 12()x→ → − − μ μ → → 1)T. . 1− − 1()x→ → − − μ μ → → 1)− − 12In⁡ ⁡ Silencio. . 1Silencio ■ T{displaystyle {frac {}{vec {x}-{vec {vec {mu }_{0}}} {m}}}} {mm} {T}Sigma _{-1}({vec) {x}-{vec # ¿Qué? Silencio {fnK}- {fnK} {fnK}- {fnMic {fnK}}_{1})} {mm} {T}Sigma {x}-{vec # {fnMicroc}}ln} 'Sigma' T} T}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/aabcd14ad0fab590180f4dd0e4d39d7aa6153edf" style="vertical-align: -1.838ex; width:80.491ex; height:5.176ex;"/>

Sin más suposiciones, el clasificador resultante se denomina análisis discriminante cuadrático (QDA).

LDA en cambio hace la suposición adicional de simplificación de la homoscedasticidad (i.e. que las covarianzas de clase son idénticas, así que ${displaystyle Sigma _{0}=Sigma _{1}=Sigma }$ ) y que las covarianzas tienen rango completo. En este caso, varios términos cancelan:

{displaystyle {vec {x}}^{mathrm {T} }Sigma _{0}^{-1}{vec {x}}={vec {x}}^{mathrm {T} }Sigma _{1}^{-1}{vec {x}}}

{displaystyle {vec {x}}^{mathrm {T} }{Sigma _{i}}^{-1}{vec {mu }}_{i}={{vec {mu }}_{i}}^{mathrm {T} }{Sigma _{i}}^{-1}{vec {x}}}

porque

{displaystyle Sigma _{i}}

Hermitian

y el criterio de decisión anterior se convierte en un umbral en el producto escalar

c}" xmlns="http://www.w3.org/1998/Math/MathML">w→ → Tx→ → ■c{displaystyle {vec {fnK} {fnMicrosoft} {fnMicrosoft}} {fnK}}} {fnMicrom}}} {fnMicrom}}}} {fnMicrom}} {T} {vec {x}}} {T}} {fn} {fn}} {fn}} {fn}} {fn}}}} {fn}}} {fn}} {fn} {fn}} {f}} {f}}}} {fn}}}}}}} {f}}}} {f}}}}}} {f}}}} {\\\f}}}}}}}} {f}}}}} {\\\\\\\\\\\\\\\\\\\fn}}}}}}}}}}}}}\\\\\\\\\\fn}}}}\\\\\\\\\\\\fn}}}}}}c}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/7d3479ae0d2b69060eccbf2cc7abaaf56de89630" style="vertical-align: -0.338ex; width:8.518ex; height:2.843ex;"/>

para alguna constante de umbral c, donde

{displaystyle {vec {w}}=Sigma ^{-1}({vec {mu }}_{1}-{vec {mu }}_{0})}

{displaystyle c={frac {1}{2}},{vec {w}}^{mathrm {T} }({vec {mu }}_{1}+{vec {mu }}_{0})}

Esto significa que el criterio de una entrada ${displaystyle {vec {x}}}$ estar en una clase ${displaystyle y}$ es puramente una función de esta combinación lineal de las observaciones conocidas.

A menudo es útil ver esta conclusión en términos geométricos: el criterio de una entrada ${displaystyle {vec {x}}}$ estar en una clase ${displaystyle y}$ es puramente una función de proyección de punto multidimensional-espacio ${displaystyle {vec {x}}}$ vector ${displaystyle {vec {w}}}$ (es decir, sólo consideramos su dirección). En otras palabras, la observación pertenece a ${displaystyle y}$ si corresponde ${displaystyle {vec {x}}}$ se encuentra en un lado determinado de un hiperplano perpendicular a ${displaystyle {vec {w}}}$ . La ubicación del plano se define por el umbral ${displaystyle c}$ .

Sumas

Los supuestos del análisis discriminante son los mismos que los de MANOVA. El análisis es bastante sensible a los valores atípicos y el tamaño del grupo más pequeño debe ser mayor que el número de variables predictoras.

Normalidad multivariable: Las variables independientes son normales para cada nivel de la variable agrupación.
Homogeneidad de la varianza/covariancia (homoscedasticidad): Las diferencias entre las variables de grupo son las mismas a través de los niveles de predictores. Se puede probar con la estadística M de Box. Se ha sugerido, sin embargo, que el análisis discriminante lineal se utilice cuando las covariancias son iguales, y que el análisis discriminante cuadrático puede utilizarse cuando las covariancias no son iguales.
Multicollinearidad: El poder predictivo puede disminuir con una mayor correlación entre variables predictoras.
Independencia: Se supone que los participantes se muestren aleatoriamente, y se supone que la puntuación de un participante en una variable es independiente de las puntuaciones en esa variable para todos los demás participantes.

Se ha sugerido que el análisis discriminante es relativamente sólido ante violaciones leves de estos supuestos, y también se ha demostrado que el análisis discriminante aún puede ser confiable cuando se utilizan variables dicotómicas (donde a menudo se viola la normalidad multivariada).

Funciones discriminantes

El análisis discriminante funciona creando una o más combinaciones lineales de predictores, creando una nueva variable latente para cada función. Estas funciones se denominan funciones discriminatorias. El número de funciones posibles es ${displaystyle N_{g}-1}$ Donde ${displaystyle N_{g}}$ = número de grupos, o ${displaystyle p}$ (el número de predictores), que sea menor. La primera función creada maximiza las diferencias entre grupos en esa función. La segunda función maximiza las diferencias en esa función, pero tampoco debe estar correlacionada con la función anterior. Esto continúa con funciones posteriores con el requisito de que la nueva función no esté relacionada con ninguna de las funciones anteriores.

Grupo dado ${displaystyle j}$ Con ${displaystyle mathbb {R} _{j}}$ conjuntos de espacio de muestra, hay una regla discriminante tal que si ${displaystyle xin mathbb {R} _{j}}$ Entonces ${displaystyle xin j}$ . Análisis descriminante entonces, encuentra regiones “buenas” de ${displaystyle mathbb {R} _{j}}$ para minimizar el error de clasificación, lo que conduce a un alto porcentaje correcto clasificado en la tabla de clasificación.

A cada función se le asigna una puntuación discriminante para determinar qué tan bien predice la ubicación del grupo.

Correlación estructural Coeficientes: La correlación entre cada predictor y la puntuación discriminatoria de cada función. Esta es una correlación de cero orden (es decir, no corregida para los otros predictores).
Coeficientes estandarizados: El peso de cada predictor en la combinación lineal que es la función discriminante. Como en una ecuación de regresión, estos coeficientes son parciales (es decir, corregidos para los otros predictores). Indica la contribución única de cada predictor en la asignación de grupo predictivo.
Funciones en Group Centroids: Las puntuaciones discriminatorias medias para cada variable de agrupación se dan para cada función. Cuanto más lejos sean los medios, menos error habrá en la clasificación.

Reglas de discriminación

Capacidad máxima: Asignaciones ${displaystyle x}$ al grupo que maximiza la densidad de población (grupo).
Bayes Discriminant Artículo: Asignaciones ${displaystyle x}$ al grupo que maximiza ${displaystyle pi _{i}f_{i}(x)}$ , donde π_i representa la probabilidad previa de esa clasificación, y ${displaystyle f_{i}(x)}$ representa la densidad de población.
Regla discriminante lineal de Fisher: Maximiza la relación entre SS_entre y SS_dentro, y encuentra una combinación lineal de los predictores para predecir grupo.

Valores propios

Un valor propio en el análisis discriminante es la raíz característica de cada función. Es una indicación de qué tan bien esa función diferencia los grupos, donde cuanto mayor es el valor propio, mejor se diferencia la función. Sin embargo, esto debe interpretarse con cautela, ya que los valores propios no tienen límite superior. El valor propio se puede ver como una relación de SS_entre y SS_dentro como en ANOVA cuando la variable dependiente es la función discriminante, y los grupos son los niveles del IV. Esto significa que el valor propio más grande está asociado con la primera función, el segundo más grande con la segunda, etc.

Tamaño del efecto

Algunos sugieren el uso de valores propios como medidas del tamaño del efecto; sin embargo, esto generalmente no se admite. En cambio, la correlación canónica es la medida preferida del tamaño del efecto. Es similar al valor propio, pero es la raíz cuadrada de la relación entre SS_entre y SS_total. Es la correlación entre grupos y la función. Otra medida popular del tamaño del efecto es el porcentaje de varianza de cada función. Esto se calcula mediante: (λ_x/Σλ_i) X 100 donde λ_x es el valor propio de la función y Σλ_i es la suma de todos los valores propios. Esto nos dice qué tan fuerte es la predicción para esa función en particular en comparación con las demás. El porcentaje clasificado correctamente también se puede analizar como tamaño del efecto. El valor kappa puede describir esto mientras se corrige la concordancia casual.Kappa normaliza todas las categorías en lugar de estar sesgado por clases con un rendimiento significativamente bueno o deficiente.

Análisis discriminante canónico para k clases

El análisis discriminante canónico (CDA) encuentra ejes (k − 1 coordenadas canónicas, siendo k el número de clases) que mejor separan las categorías. Estas funciones lineales no están correlacionadas y definen, de hecho, un espacio k − 1 óptimo a través de la nube de datos n-dimensional que mejor separa (las proyecciones en ese espacio de) los grupos k. Consulte “LDA multiclase” para obtener más detalles a continuación.

Discriminante lineal de Fisher

Los términos discriminante lineal de Fisher y LDA se usan a menudo indistintamente, aunque el artículo original de Fisher en realidad describe un discriminante ligeramente diferente, que no No haga algunos de los supuestos de LDA, como clases normalmente distribuidas o covarianzas de clases iguales.

Supongamos que dos clases de observaciones tienen medios ${displaystyle {vec {mu }}_{0},{vec {mu }}_{1}}$ y covarianzas ${displaystyle Sigma _{0},Sigma _{1}}$ . Luego la combinación lineal de características ${displaystyle {vec {w}}^{mathrm {T} }{vec {x}}}$ tendrá medios ${displaystyle {vec {w}}^{mathrm {T} }{vec {mu }}_{i}}$ y diferencias ${displaystyle {vec {w}}^{mathrm {T} }Sigma _{i}{vec {w}}}$ para ${displaystyle i=0,1}$ . Fisher definió que la separación entre estas dos distribuciones era la proporción de la diferencia entre las clases y la diferencia entre las clases:

{displaystyle S={frac {sigma _{text{between}}^{2}}{sigma _{text{within}}^{2}}}={frac {({vec {w}}cdot {vec {mu }}_{1}-{vec {w}}cdot {vec {mu }}_{0})^{2}}{{vec {w}}^{mathrm {T} }Sigma _{1}{vec {w}}+{vec {w}}^{mathrm {T} }Sigma _{0}{vec {w}}}}={frac {({vec {w}}cdot ({vec {mu }}_{1}-{vec {mu }}_{0}))^{2}}{{vec {w}}^{mathrm {T} }(Sigma _{0}+Sigma _{1}){vec {w}}}}}

Esta medida es, en cierto sentido, una medida de la relación señal-ruido para el etiquetado de clases. Se puede demostrar que la separación máxima ocurre cuando

{displaystyle {vec {w}}propto (Sigma _{0}+Sigma _{1})^{-1}({vec {mu }}_{1}-{vec {mu }}_{0})}

Cuando se cumplen los supuestos de LDA, la ecuación anterior es equivalente a LDA.

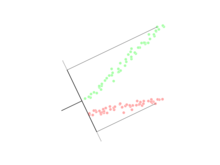
Discriminante lineal de Fisher visualizado como eje

Asegúrese de notar que el vector ${displaystyle {vec {w}}}$ es lo normal para el hiperplano discriminante. Como ejemplo, en un problema bidimensional, la línea que mejor divide los dos grupos es perpendicular a ${displaystyle {vec {w}}}$ .

En general, se proyectan los puntos de datos que deben ser objeto de discriminación ${displaystyle {vec {w}}}$ ; entonces el umbral que mejor separa los datos es elegido del análisis de la distribución unidimensional. No hay una regla general para el umbral. Sin embargo, si las proyecciones de puntos de ambas clases exhiben aproximadamente las mismas distribuciones, una buena elección sería el hiperplano entre las proyecciones de los dos medios, ${displaystyle {vec {w}}cdot {vec {mu }}_{0}}$ y ${displaystyle {vec {w}}cdot {vec {mu }}_{1}}$ . En este caso el parámetro c en estado de umbral $c}" xmlns="http://www.w3.org/1998/Math/MathML">w→ → ⋅ ⋅ x→ → ■c{displaystyle {vec}cdot {vec {x}}conoc}c}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8fe25a6aa1b34af1442727dbb7827294f90102ee" style="vertical-align: -0.338ex; width:8.778ex; height:2.343ex;"/>$ se puede encontrar explícitamente:

{displaystyle c={vec {w}}cdot {frac {1}{2}}({vec {mu }}_{0}+{vec {mu }}_{1})={frac {1}{2}}{vec {mu }}_{1}^{mathrm {T} }Sigma _{1}^{-1}{vec {mu }}_{1}-{frac {1}{2}}{vec {mu }}_{0}^{mathrm {T} }Sigma _{0}^{-1}{vec {mu }}_{0}}

El método de Otsu está relacionado con el discriminante lineal de Fisher, y fue creado para binarizar el histograma de píxeles en una imagen a escala gris seleccionando óptimamente el umbral negro/blanco que minimiza la varianza intraclase y maximiza la varianza entre las escalas de grises asignadas a clases de píxeles blanco y negro.

LDA multiclase

Visualización para ejes LDA únicos para 4 clases en 3d

Proyecciones a lo largo de ejes discriminantes lineales para 4 clases

En el caso de que haya más de dos clases, se puede ampliar el análisis utilizado en la derivación del Fisher discriminante para encontrar un subespacio que parece contener toda la variabilidad de clase. Esta generalización se debe a C. R. Rao. Supongamos que cada una de las clases C tiene una media ${displaystyle mu _{i}}$ y la misma covariancia ${displaystyle Sigma }$ . Entonces la dispersión entre variabilidad de clase puede ser definida por la covariancia de la muestra de los medios de clase

{displaystyle Sigma _{b}={frac {1}{C}}sum _{i=1}^{C}(mu _{i}-mu)(mu _{i}-mu)^{mathrm {T} }}

Donde ${displaystyle mu }$ es la media de la clase. La separación de clases en una dirección ${displaystyle {vec {w}}}$ en este caso será dado por

{displaystyle S={frac {{vec {w}}^{mathrm {T} }Sigma _{b}{vec {w}}}{{vec {w}}^{mathrm {T} }Sigma {vec {w}}}}}

Esto significa que cuando ${displaystyle {vec {w}}}$ es un eigenvector de ${displaystyle Sigma ^{-1}Sigma _{b}}$ la separación será igual al eigenvalue correspondiente.

Si ${displaystyle Sigma ^{-1}Sigma _{b}}$ es diagonalizable, la variabilidad entre las características se incluirá en el subespacio abarcado por los eigenvectores correspondientes a los C − 1 eigenvalues más grandes (desde entonces ${displaystyle Sigma _{b}}$ es de rango C − 1 al menos). Estos eigenvectores se utilizan principalmente en la reducción de características, como en PCA. Los eigenvectores correspondientes a los eigenvalues más pequeños tienden a ser muy sensibles a la elección exacta de los datos de entrenamiento, y a menudo es necesario utilizar la regularización como se describe en la siguiente sección.

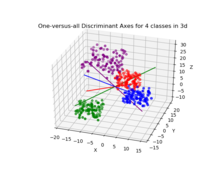
Si se requiere clasificación, en lugar de reducción de dimensiones, existen varias técnicas alternativas disponibles. Por ejemplo, las clases pueden dividirse y usarse un discriminante estándar de Fisher o LDA para clasificar cada partición. Un ejemplo común de esto es el de “uno contra el resto”. donde los puntos de una clase se colocan en un grupo y todo lo demás en el otro, y luego se aplica LDA. Esto dará como resultado clasificadores C, cuyos resultados se combinan. Otro común El método es la clasificación por pares, donde se crea un nuevo clasificador para cada par de clases (dando C(C − 1)/2 clasificadores en total), con los clasificadores individuales combinados. para producir una clasificación final.

LDA incremental

La implementación típica de la técnica LDA requiere que todas las muestras estén disponibles con anticipación. Sin embargo, hay situaciones en las que todo el conjunto de datos no está disponible y los datos de entrada se observan como una secuencia. En este caso, es deseable que la extracción de características LDA tenga la capacidad de actualizar las características LDA calculadas observando las nuevas muestras sin ejecutar el algoritmo en todo el conjunto de datos. Por ejemplo, en muchas aplicaciones en tiempo real, como la robótica móvil o el reconocimiento facial en línea, es importante actualizar las características LDA extraídas tan pronto como haya nuevas observaciones disponibles. Una técnica de extracción de características LDA que puede actualizar las características LDA simplemente observando nuevas muestras es un algoritmo LDA incremental, y esta idea se ha estudiado ampliamente durante las últimas dos décadas. Chatterjee y Roychowdhury propusieron un algoritmo LDA autoorganizado incremental para actualizar las funciones de LDA. En otro trabajo, Demir y Ozmehmet propusieron algoritmos de aprendizaje local en línea para actualizar las características de LDA de forma incremental utilizando la corrección de errores y las reglas de aprendizaje de Hebb. Posteriormente, Aliyari et all. derivó algoritmos incrementales rápidos para actualizar las características de LDA mediante la observación de las nuevas muestras.

Uso práctico

En la práctica, las medias y covarianzas de las clases no se conocen. Sin embargo, pueden estimarse a partir del conjunto de entrenamiento. Se puede utilizar la estimación de máxima verosimilitud o la estimación máxima a posteriori en lugar del valor exacto en las ecuaciones anteriores. Aunque las estimaciones de la covarianza pueden considerarse óptimas en algún sentido, esto no significa que el discriminante resultante obtenido al sustituir estos valores sea óptimo en algún sentido, incluso si el supuesto de clases distribuidas normalmente es correcto.

Otra complicación en la aplicación de LDA y el discriminante de Fisher a los datos reales ocurre cuando el número de mediciones de cada muestra (es decir, la dimensionalidad de cada vector de datos) supera el número de muestras en cada clase. En este caso, las estimaciones de covariancia no tienen rango completo, por lo que no pueden ser invertidas. Hay varias maneras de lidiar con esto. Uno es usar un pseudo inverso en lugar de la matriz habitual inverso en las fórmulas anteriores. Sin embargo, se puede lograr una mejor estabilidad numérica proyectando primero el problema en el subespacio abarcado por ${displaystyle Sigma _{b}}$ . Otra estrategia para tratar el tamaño de la muestra es utilizar un calculador de reducción de la matriz de covariancia, que puede ser expresado matemáticamente como

{displaystyle Sigma =(1-lambda)Sigma +lambda I,}

Donde ${displaystyle I}$ es la matriz de identidad, y ${displaystyle lambda }$ es Intensidad de reducción o parámetro de regularización. Esto conduce al marco del análisis discriminante regularizado o el análisis discriminante de reducción.

Además, en muchos casos prácticos los discriminantes lineales no son adecuados. LDA y el discriminante de Fisher se pueden ampliar para su uso en clasificación no lineal mediante el truco del kernel. Aquí, las observaciones originales se mapean efectivamente en un espacio no lineal de dimensiones superiores. La clasificación lineal en este espacio no lineal es entonces equivalente a la clasificación no lineal en el espacio original. El ejemplo más comúnmente utilizado de esto es el discriminante de Fisher del núcleo.

La LDA se puede generalizar a múltiples análisis discriminantes, donde c se convierte en una variable categórica con N estados posibles, en lugar de sólo dos. Analógicamente, si las densidades de clase-condicional ${displaystyle p({vec {x}}mid c=i)}$ son normales con covariancias compartidas, la estadística suficiente para ${displaystyle P(cmid {vec {x}})}$ son los valores de N proyecciones, que son el subespacio abarcado por N significa, afine proyectado por la matriz de covariancia inversa. Estas proyecciones se pueden encontrar resolviendo un problema eigenvalue generalizado, donde el numerador es la matriz de covariancia formada por tratar los medios como las muestras, y el denominador es la matriz de covariancia compartida. Ver “Multiclass LDA” arriba para más detalles.

Aplicaciones

Además de los ejemplos que se dan a continuación, LDA se aplica en el posicionamiento y la gestión de productos.

Predicción de quiebra

En la predicción de quiebras basada en ratios contables y otras variables financieras, el análisis discriminante lineal fue el primer método estadístico aplicado para explicar sistemáticamente qué empresas entraron en quiebra y qué empresas sobrevivieron. A pesar de las limitaciones, incluida la conocida no conformidad de los índices contables con los supuestos de distribución normal de LDA, el modelo de 1968 de Edward Altman sigue siendo un modelo líder en aplicaciones prácticas.

Reconocimiento facial

En el reconocimiento facial computarizado, cada rostro está representado por una gran cantidad de valores de píxeles. El análisis discriminante lineal se utiliza principalmente aquí para reducir la cantidad de características a una cantidad más manejable antes de la clasificación. Cada una de las nuevas dimensiones es una combinación lineal de valores de píxeles, que forman una plantilla. Las combinaciones lineales obtenidas utilizando el discriminante lineal de Fisher se denominan caras de Fisher, mientras que las obtenidas mediante el análisis de componentes principales relacionados se denominan caras propias.

Mercadotecnia

En la comercialización, el análisis discriminante se utilizó una vez para determinar los factores que distinguen diferentes tipos de clientes y/o productos sobre la base de encuestas u otras formas de datos recopilados. La regresión logística u otros métodos se utilizan ahora más comúnmente. El uso del análisis discriminante en la comercialización se puede describir mediante los siguientes pasos:

Formular el problema y recopilar datos — Identificar los atributos más destacados que usan los consumidores para evaluar productos en esta categoría— Utilice técnicas de investigación de marketing cuantitativo (como encuestas) para recopilar datos de una muestra de clientes potenciales acerca de sus calificaciones de todos los atributos del producto. La etapa de recopilación de datos suele ser realizada por profesionales de investigación de marketing. Las preguntas de la encuesta hacen al demandado para clasificar un producto de uno a cinco (o 1 a 7, o 1 a 10) en una gama de atributos elegidos por el investigador. En cualquier lugar de cinco a veinte atributos son elegidos. Pueden incluir cosas como: facilidad de uso, peso, precisión, durabilidad, colorido, precio o tamaño. Los atributos elegidos variarán dependiendo del producto en estudio. Se plantea la misma pregunta sobre todos los productos del estudio. Los datos para múltiples productos se codifican e ingresan en un programa estadístico como R, SPSS o SAS. (Este paso es el mismo que en el análisis de Factores).
Estimar los Coeficientes de Función Discriminante y determinar la significación y validez estadística— Elija el método de análisis discriminante adecuado. El método directo implica estimar la función discriminatoria para que todos los predictores sean evaluados simultáneamente. El método stepwise entra en los predictores secuencialmente. El método de dos grupos debe utilizarse cuando la variable dependiente tiene dos categorías o estados. El método discriminante múltiple se utiliza cuando la variable dependiente tiene tres o más estados categorizados. Use Lambda de Wilks para probar su significado en SPSS o F en SAS. El método más común utilizado para probar la validez es dividir la muestra en una muestra de estimación o análisis, y una muestra de validación o retención. La muestra de estimación se utiliza para construir la función discriminante. La muestra de validación se utiliza para construir una matriz de clasificación que contiene el número de casos correctamente clasificados e incorrectos clasificados. El porcentaje de casos correctamente clasificados se denomina ratio de.
Parcela los resultados en un mapa bidimensional, define las dimensiones e interpreta los resultados. El programa estadístico (o un módulo relacionado) mapeará los resultados. El mapa trazará cada producto (generalmente en espacio bidimensional). La distancia de los productos entre sí indica lo diferente que son. Las dimensiones deben ser etiquetadas por el investigador. Esto requiere un juicio subjetivo y a menudo es muy difícil. Ver mapa perceptual.

Estudios biomédicos

La principal aplicación del análisis discriminante en la medicina es la evaluación del estado de gravedad de un paciente y el pronóstico del resultado de la enfermedad. Por ejemplo, durante el análisis retrospectivo, los pacientes se dividen en grupos según la gravedad de la enfermedad - forma leve, moderada y severa. Luego se estudian los resultados de los análisis clínicos y de laboratorio para revelar variables estadísticamente diferentes en grupos estudiados. Utilizando estas variables, se construyen funciones discriminatorias que ayudan a clasificar objetivamente la enfermedad en un futuro paciente en forma leve, moderada o severa.

En la biología se utilizan principios similares para clasificar y definir grupos de diferentes objetos biológicos, por ejemplo, para definir tipos de phage de Salmonella enteritidis basados en espectros infrarrojos de transformación Fourier, para detectar la fuente animal de Escherichia coli estudiar sus factores de virulencia, etc.

Ciencias de la Tierra

Este método se puede utilizar para separar las zonas de alteración. Por ejemplo, cuando existen diferentes datos de varias zonas, el análisis discriminante puede encontrar el patrón dentro de los datos y clasificarlo eficazmente.

Comparación con la regresión logística

El análisis de funciones discriminantes es muy similar a la regresión logística y ambos pueden usarse para responder las mismas preguntas de investigación. La regresión logística no tiene tantos supuestos y restricciones como el análisis discriminante. Sin embargo, cuando se cumplen los supuestos del análisis discriminante, es más poderoso que la regresión logística. A diferencia de la regresión logística, el análisis discriminante se puede utilizar con muestras de tamaño pequeño. Se ha demostrado que cuando los tamaños de muestra son iguales y se mantiene la homogeneidad de la varianza/covarianza, el análisis discriminante es más preciso. A pesar de todas estas ventajas, la regresión logística se ha convertido en la opción común, ya que rara vez se cumplen los supuestos del análisis discriminante.

Discriminante lineal en dimensiones altas

Las anomalías geométricas en dimensiones superiores conducen a la conocida maldición de la dimensionalidad. Sin embargo, la utilización adecuada de los fenómenos de concentración de medidas puede facilitar el cálculo. Donoho y Tanner destacaron un caso importante de estos fenómenos de bendición de dimensionalidad: si una muestra es esencialmente de alta dimensión, entonces cada punto puede separarse del resto de la muestra mediante desigualdad lineal, con alta probabilidad, incluso para muestras exponencialmente grandes. Estas desigualdades lineales se pueden seleccionar en la forma estándar (de Fisher) del discriminante lineal para una familia rica de distribución de probabilidad. En particular, tales teoremas se prueban para distribuciones log-cóncavas, incluida la distribución normal multidimensional (la prueba se basa en las desigualdades de concentración para medidas log-cóncavas) y para medidas de productos en un cubo multidimensional (esto se prueba usando la concentración de Talagrand). desigualdad para espacios de probabilidad del producto). La separabilidad de datos mediante discriminantes lineales clásicos simplifica el problema de corrección de errores para sistemas de inteligencia artificial en alta dimensión.

Más resultados...