Análisis de variación

Análisis de varianza (ANOVA) es una colección de modelos estadísticos y sus procedimientos de estimación asociados (como la "variación" entre grupos y) utilizado para analizar las diferencias entre medias. ANOVA fue desarrollado por el estadístico Ronald Fisher. ANOVA se basa en la ley de la varianza total, donde la varianza observada en una variable particular se divide en componentes atribuibles a diferentes fuentes de variación. En su forma más simple, ANOVA proporciona una prueba estadística de si dos o más medias de población son iguales y, por lo tanto, generaliza la prueba t más allá de dos medias. En otras palabras, el ANOVA se usa para probar la diferencia entre dos o más medias.

Historia

Mientras que el análisis de la varianza llegó a buen término en el siglo XX, los antecedentes se remontan siglos atrás, según Stigler. Estos incluyen la prueba de hipótesis, la partición de sumas de cuadrados, técnicas experimentales y el modelo aditivo. Laplace estaba realizando pruebas de hipótesis en la década de 1770. Alrededor de 1800, Laplace y Gauss desarrollaron el método de mínimos cuadrados para combinar observaciones, que mejoró los métodos que se usaban entonces en astronomía y geodesia. También inició mucho estudio de las contribuciones a las sumas de cuadrados. Laplace sabía cómo estimar una varianza a partir de una suma de cuadrados residual (en lugar de un total). En 1827, Laplace estaba utilizando métodos de mínimos cuadrados para abordar los problemas de ANOVA con respecto a las mediciones de las mareas atmosféricas. Antes de 1800, los astrónomos tenían errores de observación aislados que resultaban de los tiempos de reacción (la "ecuación personal") y había desarrollado métodos para reducir los errores. Los métodos experimentales utilizados en el estudio de la ecuación personal fueron aceptados más tarde por el campo emergente de la psicología que desarrolló métodos experimentales fuertes (factoriales completos) a los que pronto se agregaron la aleatorización y el cegamiento. Una elocuente explicación no matemática del modelo de efectos aditivos estaba disponible en 1885.

Ronald Fisher introdujo el término varianza y propuso su análisis formal en un artículo de 1918 La correlación entre parientes sobre la suposición de la herencia mendeliana. Su primera aplicación del análisis de varianza se publicó en 1921. El análisis de varianza se hizo ampliamente conocido después de ser incluido en el libro Statistical Methods for Research Workers de Fisher de 1925.

Varios investigadores desarrollaron modelos de aleatorización. El primero fue publicado en polaco por Jerzy Neyman en 1923.

Ejemplo

No cabe: Joven vs viejo, y de pelo corto vs de pelo largo

Ideal: Pet vs raza de trabajo y menos atlético vs más atlético

Muy buen ajuste: Peso por raza

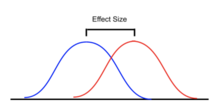
El análisis de varianza se puede utilizar para describir relaciones complejas entre variables. Una exposición canina proporciona un ejemplo. Una exposición canina no es una muestra aleatoria de la raza: generalmente se limita a perros adultos, de raza pura y ejemplares. Es plausible que un histograma de pesos de perros de un espectáculo sea bastante complejo, como la distribución amarillo-naranja que se muestra en las ilustraciones. Supongamos que quisiéramos predecir el peso de un perro en función de un determinado conjunto de características de cada perro. Una forma de hacerlo es explicar la distribución de pesos dividiendo la población de perros en grupos según esas características. Un agrupamiento exitoso dividirá a los perros de tal manera que (a) cada grupo tenga una varianza baja en el peso de los perros (lo que significa que el grupo es relativamente homogéneo) y (b) la media de cada grupo sea distinta (si dos grupos tienen la misma media, entonces no es razonable concluir que los grupos están, de hecho, separados de manera significativa).

En las ilustraciones de la derecha, los grupos se identifican como X₁, X₂, etc. En la primera ilustración, los perros se dividen según el producto (interacción) de dos agrupaciones binarias: jóvenes frente a viejos, y de pelo corto frente a pelo largo (p. ej., el grupo 1 son perros jóvenes de pelo corto, el grupo 2 son perros jóvenes, perros de pelo largo, etc.). Dado que las distribuciones del peso de los perros dentro de cada uno de los grupos (que se muestran en azul) tienen una variación relativamente grande, y dado que las medias son muy similares entre los grupos, agrupar a los perros por estas características no produce una forma efectiva de explicar la variación en los pesos de los perros.: saber en qué grupo está un perro no nos permite predecir su peso mucho mejor que simplemente saber que el perro está en una exposición canina. Por lo tanto, esta agrupación no logra explicar la variación en la distribución general (amarillo-naranja).

Un intento de explicar la distribución del peso agrupando a los perros como mascotas frente a razas de trabajo y menos atléticos frente a más atléticos probablemente tendría algo más de éxito (ajuste justo). Es probable que los perros de exhibición más pesados sean de razas grandes, fuertes y trabajadoras, mientras que las razas que se mantienen como mascotas tienden a ser más pequeñas y, por lo tanto, más livianas. Como muestra la segunda ilustración, las distribuciones tienen varianzas considerablemente menores que en el primer caso, y las medias son más distinguibles. Sin embargo, la superposición significativa de distribuciones, por ejemplo, significa que no podemos distinguir X₁ y X₂ de manera confiable. Agrupar perros de acuerdo con el lanzamiento de una moneda podría producir distribuciones similares.

Es probable que un intento de explicar el peso por raza produzca un ajuste muy bueno. Todos los chihuahuas son ligeros y todos los san bernardos son pesados. La diferencia de peso entre Setters y Pointers no justifica razas separadas. El análisis de varianza proporciona las herramientas formales para justificar estos juicios intuitivos. Un uso común del método es el análisis de datos experimentales o el desarrollo de modelos. El método tiene algunas ventajas sobre la correlación: no todos los datos deben ser numéricos y un resultado del método es un juicio sobre la confianza en una relación explicativa.

Clases de modelos

Hay tres clases de modelos utilizados en el análisis de varianza, y estos se describen aquí.

Modelos de efectos fijos

El modelo de efectos fijos (clase I) de análisis de varianza se aplica a situaciones en las que el experimentador aplica uno o más tratamientos a los sujetos del experimento para ver si los valores de las variables de respuesta cambian. Esto permite al experimentador estimar los rangos de valores de las variables de respuesta que el tratamiento generaría en la población como un todo.

Efectos fijos vs Efectos aleatorios

Modelos de efectos aleatorios

El modelo de efectos aleatorios (clase II) se utiliza cuando los tratamientos no son fijos. Esto ocurre cuando los diversos niveles de factor se muestrean de una población más grande. Debido a que los niveles en sí son variables aleatorias, algunas suposiciones y el método de contrastar los tratamientos (una generalización multivariable de diferencias simples) difieren del modelo de efectos fijos.

Modelos de efectos mixtos

Un modelo de efectos mixtos (clase III) contiene factores experimentales de tipos de efectos fijos y aleatorios, con interpretaciones y análisis apropiadamente diferentes para los dos tipos.

Ejemplo

Los experimentos de enseñanza pueden ser realizados por un colegio o departamento universitario para encontrar un buen libro de texto introductorio, con cada texto considerado como un tratamiento. El modelo de efectos fijos compararía una lista de textos candidatos. El modelo de efectos aleatorios determinaría si existen diferencias importantes entre una lista de textos seleccionados al azar. El modelo de efectos mixtos compararía los textos vigentes (fijos) con alternativas seleccionadas al azar.

La definición de efectos fijos y aleatorios ha resultado difícil de alcanzar, y se puede decir que las definiciones contrapuestas conducen a un atolladero lingüístico.

Supuestos

El análisis de varianza se ha estudiado desde varios enfoques, el más común de los cuales utiliza un modelo lineal que relaciona la respuesta a los tratamientos y bloques. Tenga en cuenta que el modelo es lineal en los parámetros, pero puede ser no lineal a través de los niveles de los factores. La interpretación es fácil cuando los datos están equilibrados entre factores, pero se necesita una comprensión mucho más profunda para los datos no equilibrados.

Análisis de libros de texto utilizando una distribución normal

El análisis de varianza se puede presentar en términos de un modelo lineal, que hace las siguientes suposiciones sobre la distribución de probabilidad de las respuestas:

• Independencia de las observaciones – esta es una suposición del modelo que simplifica el análisis estadístico.
• Normalidad – las distribuciones de los residuos son normales.
• Igualdad (o "homogeneidad") de las diferencias, llamada homoscedasticidad, la variabilidad de los datos en grupos debe ser la misma.

Las suposiciones separadas del modelo de libro de texto implican que los errores son independientemente, idénticos y normalmente distribuidos para modelos de efectos fijos, es decir, que los errores (${displaystyle varepsilon }$) son independientes y

$${displaystyle varepsilon thicksim N(0,sigma ^{2}). }$$

Análisis basado en la aleatorización

En un experimento controlado aleatorio, los tratamientos se asignan aleatoriamente a las unidades experimentales, siguiendo el protocolo experimental. Esta aleatorización es objetiva y declarada antes de realizar el experimento. La asignación aleatoria objetiva se utiliza para probar la significación de la hipótesis nula, siguiendo las ideas de C. S. Peirce y Ronald Fisher. Este análisis basado en el diseño fue discutido y desarrollado por Francis J. Anscombe en la Estación Experimental de Rothamsted y por Oscar Kempthorne en la Universidad Estatal de Iowa. Kempthorne y sus estudiantes asumen la aditividad del tratamiento de unidades, que se analiza en los libros de Kempthorne y David R. Cox.

Aditividad por unidad de tratamiento

En su forma más simple, la asunción de la aditividad del tratamiento unitario indica que la respuesta observada ${displaystyle y_{i,j}$ de la unidad experimental ${displaystyle i}$ cuando recibe tratamiento ${displaystyle j}$ puede ser escrito como la suma de la respuesta de la unidad ${displaystyle Y...$ y el efecto de tratamiento ${displaystyle t_{j}$, eso es

$${displaystyle Y...$$

${displaystyle j}$

${displaystyle j}$

${displaystyle t_{j}$

La suposición de la aditividad del tratamiento unitario por lo general no se puede falsificar directamente, según Cox y Kempthorne. Sin embargo, se pueden falsificar muchas consecuencias de la aditividad de la unidad de tratamiento. Para un experimento aleatorizado, la suposición de aditividad de tratamiento unitario implica que la varianza es constante para todos los tratamientos. Por lo tanto, por contraposición, una condición necesaria para la aditividad del tratamiento unitario es que la varianza sea constante.

El uso de la aditividad del tratamiento de unidades y la aleatorización es similar a la inferencia basada en el diseño que es estándar en el muestreo de encuestas de población finita.

Modelo lineal derivado

Kempthorne usa la distribución aleatoria y la suposición de aditividad de tratamiento de unidades para producir un modelo lineal derivado, muy similar al modelo de libro de texto discutido anteriormente. Las estadísticas de prueba de este modelo lineal derivado se aproximan estrechamente a las estadísticas de prueba de un modelo lineal normal apropiado, de acuerdo con teoremas de aproximación y estudios de simulación. Sin embargo, hay diferencias. Por ejemplo, el análisis basado en la aleatorización da como resultado una correlación pequeña pero (estrictamente) negativa entre las observaciones. En el análisis basado en la aleatorización, no hay ninguna suposición de una distribución normal y ciertamente ninguna suposición de independencia. ¡Al contrario, las observaciones son dependientes!

El análisis basado en la aleatorización tiene la desventaja de que su exposición implica un álgebra tediosa y un tiempo extenso. Dado que el análisis basado en la aleatorización es complicado y se aproxima mucho al enfoque que usa un modelo lineal normal, la mayoría de los maestros enfatizan el enfoque del modelo lineal normal. Pocos estadísticos se oponen al análisis basado en modelos de experimentos aleatorios balanceados.

Modelos estadísticos para datos observacionales

Sin embargo, cuando se aplica a datos de experimentos no aleatorios o estudios observacionales, el análisis basado en modelos carece de la garantía de la aleatorización. Para los datos observacionales, la derivación de los intervalos de confianza debe utilizar modelos subjetivos, como enfatizan Ronald Fisher y sus seguidores. En la práctica, las estimaciones de los efectos del tratamiento de los estudios de observación suelen ser inconsistentes. En la práctica, los "modelos estadísticos" y los datos de observación son útiles para sugerir hipótesis que el público debe tratar con mucha cautela.

Resumen de supuestos

El análisis ANOVA basado en el modelo normal asume la independencia, normalidad y homogeneidad de las varianzas de los residuos. El análisis basado en la aleatorización asume únicamente la homogeneidad de las varianzas de los residuos (como consecuencia de la aditividad de la unidad de tratamiento) y utiliza el procedimiento de aleatorización del experimento. Ambos análisis requieren homocedasticidad, como suposición para el análisis del modelo normal y como consecuencia de la aleatorización y la aditividad para el análisis basado en la aleatorización.

Sin embargo, los estudios de procesos que cambian las varianzas en lugar de las medias (llamados efectos de dispersión) se han realizado con éxito mediante ANOVA. No hay ninguna suposición necesaria para ANOVA en toda su generalidad, pero la prueba F utilizada para la prueba de hipótesis de ANOVA tiene suposiciones y prácticas. limitaciones que son de interés permanente.

Los problemas que no satisfacen las suposiciones de ANOVA a menudo se pueden transformar para satisfacer las suposiciones. La propiedad de aditividad de tratamiento unitario no es invariante bajo un 'cambio de escala', por lo que los estadísticos a menudo usan transformaciones para lograr la aditividad de tratamiento unitario. Si se espera que la variable de respuesta siga una familia paramétrica de distribuciones de probabilidad, entonces el estadístico puede especificar (en el protocolo del experimento o estudio observacional) que las respuestas se transformen para estabilizar la varianza. Además, un estadístico puede especificar que se apliquen transformaciones logarítmicas a las respuestas, que se cree que siguen un modelo multiplicativo. Según el teorema de la ecuación funcional de Cauchy, el logaritmo es la única transformación continua que transforma la multiplicación real en suma.

Características

ANOVA se utiliza en el análisis de experimentos comparativos, aquellos en los que solo interesa la diferencia en los resultados. La significación estadística del experimento está determinada por una relación de dos varianzas. Esta relación es independiente de varias alteraciones posibles a las observaciones experimentales: agregar una constante a todas las observaciones no altera la significación. Multiplicar todas las observaciones por una constante no altera el significado. Por lo tanto, el resultado de significación estadística de ANOVA es independiente del sesgo constante y los errores de escala, así como de las unidades utilizadas para expresar las observaciones. En la era del cálculo mecánico, era común restar una constante de todas las observaciones (cuando era equivalente a eliminar los dígitos principales) para simplificar la entrada de datos. Este es un ejemplo de codificación de datos.

Lógica

Los cálculos de ANOVA se pueden caracterizar por calcular una cantidad de medias y varianzas, dividir dos varianzas y comparar la relación con un valor manual para determinar la significancia estadística. Entonces, calcular el efecto de un tratamiento es trivial: "el efecto de cualquier tratamiento se estima tomando la diferencia entre la media de las observaciones que reciben el tratamiento y la media general".

Partición de la suma de cuadrados

ANOVA utiliza terminología estandarizada tradicional. La ecuación de la varianza de la muestra es ${fn1}fn1} - Sí.$, donde el divisor se llama los grados de libertad (DF), se llama la suma la suma de cuadrados (SS), el resultado se llama el cuadrado medio (MS) y los términos cuadrados son desviaciones del medio de la muestra. ANOVA estima 3 diferencias de muestra: una varianza total basada en todas las desviaciones de observación del gran medio, una varianza de error basada en todas las desviaciones de observación de sus medios adecuados de tratamiento, y una varianza de tratamiento. La diferencia de tratamiento se basa en las desviaciones del tratamiento significa que el resultado se multiplica por el número de observaciones en cada tratamiento para tener en cuenta la diferencia entre la diferencia de observaciones y la diferencia de medios.

La técnica fundamental es una partición de la suma total de cuadrados SS en componentes relacionados con los efectos utilizados en el modelo. Por ejemplo, el modelo para un ANOVA simplificado con un tipo de tratamiento en diferentes niveles.

$${displaystyle SS.$$

El número de grados de libertad DF se puede dividir de manera similar: uno de estos componentes (el del error) especifica una distribución de chi-cuadrado que describe la suma de cuadrados asociada, mientras que el Lo mismo es cierto para los "tratamientos" si no hay efecto del tratamiento.

$${displaystyle DF_{text{Total}=DF_{text{Error}+DF_{text{Treatments}}$$

La prueba F

La prueba F se utiliza para comparar los factores de la desviación total. Por ejemplo, en ANOVA unidireccional o de factor único, la significancia estadística se prueba comparando la estadística de prueba F

$${displaystyle F={fractext{variance between treatments}{text{variance within treatments}}}}$$

$${displaystyle F={frac {MS_{text{Treatments}}} {MS_{text{Error}}={SS_{text{Treatments}}/(I-1)}over {text{Error}/(n_{T}-I)}}}}}}}}}}}}}}}}}}} {f} {f} {f}}}}}}}}}}}}}}}}}}}}}} {f}} {f}} {f}} {f} {f}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$$

Donde MS es cuadrado malo, ${displaystyle Yo...$ es el número de tratamientos y ${displaystyle No.$ es el número total de casos

a la F-distribución con ${displaystyle I-1}$, ${displaystyle No.$ grados de libertad. Usando el F- La distribución es un candidato natural porque la estadística de prueba es la relación de dos sumas escalonadas de cuadrados cada uno de los cuales sigue una distribución escalonada de chi.

El valor esperado de F es ${displaystyle 1+{nsigma _{text{Treatment} {2}/{sigma} - ¿Qué?$ (donde) ${displaystyle n}$ es el tamaño de la muestra de tratamiento) que es 1 para ningún efecto de tratamiento. Como valores de aumento F por encima de 1, la evidencia es cada vez más inconsistente con la hipótesis nula. Dos métodos experimentales aparentes de aumento de F aumentan el tamaño de la muestra y reducen la diferencia de error mediante controles experimentales estrictos.

Hay dos métodos para concluir la prueba de hipótesis ANOVA, y ambos producen el mismo resultado:

• El método textbook es comparar el valor observado de F con el valor crítico de F determinado en tablas. El valor crítico de F es una función de los grados de libertad del numerador y del denominador y el nivel de significación (α). Si F ≥ F_Crítica, la hipótesis nula es rechazada.
• El método informático calcula la probabilidad (valor p) de un valor de F mayor o igual al valor observado. La hipótesis nula es rechazada si esta probabilidad es inferior o igual al nivel de significación (o igual al nivel de significación)α).

Se sabe que la prueba F de ANOVA es casi óptima en el sentido de que minimiza los errores de falsos negativos para una tasa fija de errores de falsos positivos (es decir, maximiza el poder para un nivel de significación fijo). Por ejemplo, para probar la hipótesis de que varios tratamientos médicos tienen exactamente el mismo efecto, los valores p de la prueba F se aproximan mucho a los valores p de la prueba de permutación: la aproximación es particularmente cercano cuando el diseño es equilibrado. Tales pruebas de permutación caracterizan pruebas con máxima potencia contra todas las hipótesis alternativas, como observó Rosenbaum. La prueba ANOVA F (de la hipótesis nula de que todos los tratamientos tienen exactamente el mismo efecto) se recomienda como prueba práctica, debido a su robustez frente a muchas distribuciones alternativas.

Lógica extendida

ANOVA consta de partes separables; las fuentes de particionamiento de la varianza y la prueba de hipótesis se pueden usar individualmente. ANOVA se utiliza para apoyar otras herramientas estadísticas. La regresión se usa primero para ajustar modelos más complejos a los datos, luego se usa ANOVA para comparar modelos con el objetivo de seleccionar modelos simples (r) que describan adecuadamente los datos. "Tales modelos podrían ajustarse sin ninguna referencia a ANOVA, pero las herramientas de ANOVA podrían luego usarse para dar algún sentido a los modelos ajustados y para probar hipótesis sobre lotes de coeficientes." "[P]ensamos en el análisis de varianza como una forma de comprender y estructurar modelos multinivel, no como una alternativa a la regresión, sino como una herramienta para resumir inferencias complejas de alta dimensión..."

Para un solo factor

El experimento más simple adecuado para el análisis ANOVA es el experimento completamente aleatorio con un solo factor. Los experimentos más complejos con un solo factor implican restricciones en la aleatorización e incluyen bloques completamente aleatorios y cuadrados latinos (y variantes: cuadrados greco-latinos, etc.). Los experimentos más complejos comparten muchas de las complejidades de múltiples factores. Se encuentra disponible una discusión relativamente completa del análisis (modelos, resúmenes de datos, tabla ANOVA) del experimento completamente aleatorizado.

Existen algunas alternativas al análisis de varianza unidireccional convencional, por ejemplo: prueba F heteroscedástica de Welch, prueba F heteroscedástica de Welch con medias recortadas y varianzas Winsorizadas, prueba de Brown-Forsythe, Alexander-Govern prueba, prueba de segundo orden de James y prueba de Kruskal-Wallis, disponibles en onewaytests R

Es útil representar cada punto de datos de la siguiente forma, llamada modelo estadístico:

$${displaystyle Y... +tau _{j}+varepsilon ¿Qué?$$

• i = 1, 2, 3,... R
• j = 1, 2, 3,... C
• μ = promedio general (medio)
• τ_j = efecto diferencial (respuesta) asociado con el j nivel de X;
  esto supone que en general los valores τ_j añadir a cero (es decir, ${textstyle sum _{j=1}{C}tau _{j}=0}$)
• ε_ij = ruido o error asociado con el particular ij Valor de datos

Es decir, visualizamos un modelo aditivo que dice que cada punto de datos se puede representar sumando tres cantidades: la verdadera media, promediada sobre todos los niveles de factor que se están investigando, más un componente incremental asociado con la columna particular (nivel de factor), más un componente final asociado con todo lo demás que afecta ese valor de datos específico.

Para múltiples factores

ANOVA se generaliza para el estudio de los efectos de múltiples factores. Cuando el experimento incluye observaciones en todas las combinaciones de niveles de cada factor, se denomina factorial. Los experimentos factoriales son más eficientes que una serie de experimentos de un solo factor y la eficiencia crece a medida que aumenta el número de factores. En consecuencia, los diseños factoriales son muy utilizados.

El uso de ANOVA para estudiar los efectos de múltiples factores tiene una complicación. En un ANOVA de 3 vías con factores x, y y z, el modelo ANOVA incluye términos para los efectos principales (x, y, z) y términos para interacciones (xy, xz, yz, xyz). Todos los términos requieren pruebas de hipótesis. La proliferación de términos de interacción aumenta el riesgo de que alguna prueba de hipótesis produzca un falso positivo por casualidad. Afortunadamente, la experiencia dice que las interacciones de alto orden son raras. La capacidad de detectar interacciones es una gran ventaja del ANOVA de múltiples factores. Probar un factor a la vez oculta interacciones, pero produce resultados experimentales aparentemente inconsistentes.

Se recomienda precaución al encontrar interacciones; Primero pruebe los términos de interacción y amplíe el análisis más allá de ANOVA si se encuentran interacciones. Los textos varían en sus recomendaciones con respecto a la continuación del procedimiento ANOVA después de encontrar una interacción. Las interacciones complican la interpretación de los datos experimentales. Ni los cálculos de importancia ni los efectos estimados del tratamiento pueden tomarse al pie de la letra. "Una interacción significativa a menudo enmascarará la importancia de los efectos principales." Se recomiendan métodos gráficos para mejorar la comprensión. La regresión suele ser útil. En Cox (1958) se encuentra disponible una extensa discusión sobre las interacciones. Algunas interacciones se pueden eliminar (mediante transformaciones) mientras que otras no.

Se utiliza una variedad de técnicas con ANOVA de múltiples factores para reducir los gastos. Una técnica utilizada en los diseños factoriales es minimizar la replicación (posiblemente sin replicación con el apoyo de trucos analíticos) y combinar grupos cuando se descubre que los efectos son estadísticamente (o prácticamente) insignificantes. Un experimento con muchos factores insignificantes puede colapsar en uno con pocos factores respaldados por muchas repeticiones.

Análisis asociado

Se requieren algunos análisis para respaldar el diseño del experimento, mientras que otros análisis se realizan después de que se determina formalmente que los cambios en los factores producen cambios estadísticamente significativos en las respuestas. Debido a que la experimentación es iterativa, los resultados de un experimento alteran los planes para los siguientes experimentos.

Análisis preparatorio

El número de unidades experimentales

En el diseño de un experimento, se planifica el número de unidades experimentales para satisfacer los objetivos del experimento. La experimentación es a menudo secuencial.

Los primeros experimentos a menudo están diseñados para proporcionar estimaciones medias imparciales de los efectos del tratamiento y del error experimental. Los experimentos posteriores a menudo están diseñados para probar una hipótesis de que el efecto de un tratamiento tiene una magnitud importante; en este caso, el número de unidades experimentales se elige para que el experimento esté dentro del presupuesto y tenga la potencia adecuada, entre otros objetivos.

Por lo general, en psicología se requiere informar el análisis del tamaño de la muestra. "Proporcionar información sobre el tamaño de la muestra y el proceso que condujo a las decisiones sobre el tamaño de la muestra." El análisis, que está escrito en el protocolo experimental antes de realizar el experimento, se examina en las solicitudes de subvención y en las juntas de revisión administrativa.

Además del análisis de potencia, existen métodos menos formales para seleccionar el número de unidades experimentales. Estos incluyen métodos gráficos basados en limitar la probabilidad de errores de falsos negativos, métodos gráficos basados en un aumento de variación esperado (por encima de los residuos) y métodos basados en lograr un intervalo de confianza deseado.

Análisis de potencia

El análisis de poder se aplica a menudo en el contexto de ANOVA para evaluar la probabilidad de rechazar con éxito la hipótesis nula si asumimos un determinado diseño de ANOVA, tamaño del efecto en la población, tamaño de la muestra y nivel de significación. El análisis de potencia puede ayudar en el diseño del estudio al determinar qué tamaño de muestra sería necesario para tener una posibilidad razonable de rechazar la hipótesis nula cuando la hipótesis alternativa es verdadera.

Tamaño del efecto

Tamaño del efecto

Se han propuesto varias medidas de efecto estandarizadas para ANOVA para resumir la fuerza de la asociación entre uno o varios predictores y la variable dependiente o la diferencia estandarizada general del modelo completo. Las estimaciones estandarizadas del tamaño del efecto facilitan la comparación de hallazgos entre estudios y disciplinas. Sin embargo, mientras que los tamaños del efecto estandarizados se usan comúnmente en gran parte de la literatura profesional, una medida no estandarizada del tamaño del efecto que tiene un efecto inmediatamente "significativo" las unidades pueden ser preferibles para propósitos de informes.

Confirmación del modelo

A veces se realizan pruebas para determinar si las suposiciones de ANOVA parecen haber sido violadas. Los residuos se examinan o analizan para confirmar la homocedasticidad y la normalidad bruta. Los residuos deben tener la apariencia de ruido (distribución normal media cero) cuando se grafican como una función de cualquier cosa, incluido el tiempo y valores de datos modelados. Las tendencias apuntan a interacciones entre factores o entre observaciones.

Pruebas de seguimiento

Un efecto estadísticamente significativo en ANOVA suele ir seguido de pruebas adicionales. Esto se puede hacer para evaluar qué grupos son diferentes de otros grupos o para probar varias otras hipótesis enfocadas. Las pruebas de seguimiento a menudo se distinguen en términos de si están "planificadas" (a priori) o "post hoc." Las pruebas planificadas se determinan antes de mirar los datos, y las pruebas post hoc se conciben solo después de mirar los datos (aunque el término 'post hoc' se usa de manera inconsistente).

Las pruebas de seguimiento pueden ser "simples" comparaciones por pares de medias de grupos individuales o pueden ser "compuestas" comparaciones (p. ej., comparar la agrupación media entre los grupos A, B y C con la media del grupo D). Las comparaciones también pueden analizar pruebas de tendencia, como relaciones lineales y cuadráticas, cuando la variable independiente implica niveles ordenados. A menudo, las pruebas de seguimiento incorporan un método de ajuste para el problema de las comparaciones múltiples.

Las pruebas de seguimiento para identificar qué grupos, variables o factores específicos tienen medias estadísticamente diferentes incluyen la prueba de rango de Tukey y la nueva prueba de rango múltiple de Duncan. A su vez, estas pruebas a menudo se siguen con una metodología de visualización de letras compactas (CLD) para que el resultado de las pruebas mencionadas sea más transparente para una audiencia que no es estadística.

Diseños de estudio

Hay varios tipos de ANOVA. Muchos estadísticos basan ANOVA en el diseño del experimento, especialmente en el protocolo que especifica la asignación aleatoria de tratamientos a los sujetos; la descripción del protocolo del mecanismo de asignación debe incluir una especificación de la estructura de los tratamientos y de cualquier bloqueo. También es común aplicar ANOVA a datos observacionales usando un modelo estadístico apropiado.

Algunos diseños populares usan los siguientes tipos de ANOVA:

• Una vía ANOVA se utiliza para probar diferencias entre dos o más grupos independientes (medios), por ejemplo, diferentes niveles de aplicación de urea en un cultivo, o diferentes niveles de acción antibiótica en varias especies bacterianas diferentes, o diferentes niveles de efecto de algunos medicamentos en grupos de pacientes. Sin embargo, si estos grupos no son independientes, y hay un orden en los grupos (como enfermedad leve, moderada y severa), o en la dosis de un medicamento (como 5 mg/mL, 10 mg/mL, 20 mg/mL) dado al mismo grupo de pacientes, entonces se debe utilizar una estimación de tendencia lineal. Típicamente, sin embargo, la única vía ANOVA se utiliza para probar las diferencias entre al menos tres grupos, ya que el caso de dos grupos puede ser cubierto por una prueba t. Cuando hay sólo dos medios para comparar, la prueba t y la prueba ANOVA F son equivalentes; la relación entre ANOVA y ANOVA t es dado por F = t².
• Factorial ANOVA se utiliza cuando hay más de un factor.
• Medidas repetidas ANOVA se utiliza cuando se utilizan los mismos temas para cada factor (por ejemplo, en un estudio longitudinal).
• El análisis multivariable de la varianza (MANOVA) se utiliza cuando hay más de una variable de respuesta.

Precauciones

Los experimentos equilibrados (aquellos con un tamaño de muestra igual para cada tratamiento) son relativamente fáciles de interpretar; los experimentos desequilibrados ofrecen más complejidad. Para ANOVA de factor único (unidireccional), el ajuste para datos desequilibrados es fácil, pero el análisis desequilibrado carece tanto de robustez como de potencia. Para diseños más complejos, la falta de equilibrio genera más complicaciones. "La propiedad de ortogonalidad de los principales efectos e interacciones presentes en los datos balanceados no se traslada al caso no balanceado. Esto significa que no se aplican las técnicas habituales de análisis de varianza. En consecuencia, el análisis de factoriales no balanceados es mucho más difícil que el de diseños balanceados." En el caso general, "El análisis de varianza también se puede aplicar a datos no balanceados, pero luego las sumas de los cuadrados, los cuadrados medios y las razones F dependerán del orden en que se se consideran las fuentes de variación."

ANOVA es (en parte) una prueba de significación estadística. La Asociación Estadounidense de Psicología (y muchas otras organizaciones) opina que simplemente informar sobre la significación estadística es insuficiente y que se prefiere informar sobre los límites de confianza.

Generalizaciones

ANOVA se considera un caso especial de regresión lineal que, a su vez, es un caso especial del modelo lineal general. Todos consideran que las observaciones son la suma de un modelo (ajuste) y un residuo (error) a minimizar.

La prueba de Kruskal-Wallis y la prueba de Friedman son pruebas no paramétricas, que no se basan en una suposición de normalidad.

Conexión a la regresión lineal

A continuación, aclaramos la conexión entre el ANOVA multidireccional y la regresión lineal.

Reordenar linealmente los datos para que ${displaystyle k}$-la observación se asocia con una respuesta ${displaystyle y_{k}$ y factores ${displaystyle Z_{k,b}$ Donde ${displaystyle bin {1,2,ldots B}$ denota los diferentes factores y ${displaystyle B}$ es el número total de factores. En un solo sentido ANOVA ${displaystyle B=1}$ y en dos sentidos ANOVA ${displaystyle B=2}$. Además, asumimos el ${displaystyle b}$- el factor tiene ${displaystyle I_{b}$ niveles: ${displaystyle {1,2,ldotsI_{b}}}$. Ahora, podemos codificar los factores en el ${textstyle sum ¿Qué?$ vector dimensional ${displaystyle V_{k}$.

La función de codificación de un solo toque ${displaystyle g_{b}:{1,2,ldotsI_{b}mapsto {0,1} {I_{b}}}$ se define tal que ${displaystyle i}$-la entrada ${displaystyle g_{b}(Z_{k,b}}$ es